Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2004 AMC 12A Problems/Problem 18"
m (→‎Solution 4)
 
(61 intermediate revisions by 20 users not shown)
Line 1: Line 1:
 
{{duplicate|[[2004 AMC 12A Problems|2004 AMC 12A #18]] and [[2004 AMC 10A Problems/Problem 22|2004 AMC 10A #22]]}}
 
{{duplicate|[[2004 AMC 12A Problems|2004 AMC 12A #18]] and [[2004 AMC 10A Problems/Problem 22|2004 AMC 10A #22]]}}
  
−
==Problem==
+
== Problem ==
 
[[Square]] <math>ABCD</math> has side length <math>2</math>. A [[semicircle]] with [[diameter]] <math>\overline{AB}</math> is constructed inside the square, and the [[tangent (geometry)|tangent]] to the semicircle from <math>C</math> intersects side <math>\overline{AD}</math> at <math>E</math>. What is the length of <math>\overline{CE}</math>?
 
[[Square]] <math>ABCD</math> has side length <math>2</math>. A [[semicircle]] with [[diameter]] <math>\overline{AB}</math> is constructed inside the square, and the [[tangent (geometry)|tangent]] to the semicircle from <math>C</math> intersects side <math>\overline{AD}</math> at <math>E</math>. What is the length of <math>\overline{CE}</math>?
  
Line 19: Line 19:
 
<math> \mathrm{(A) \ } \frac{2+\sqrt{5}}{2} \qquad \mathrm{(B) \ } \sqrt{5} \qquad \mathrm{(C) \ } \sqrt{6} \qquad \mathrm{(D) \ } \frac{5}{2} \qquad \mathrm{(E) \ } 5-\sqrt{5} </math>
 
<math> \mathrm{(A) \ } \frac{2+\sqrt{5}}{2} \qquad \mathrm{(B) \ } \sqrt{5} \qquad \mathrm{(C) \ } \sqrt{6} \qquad \mathrm{(D) \ } \frac{5}{2} \qquad \mathrm{(E) \ } 5-\sqrt{5} </math>
  
−
__TOC__
+
== Solutions ==
−
== Solution 1 ==
+
=== Solution 1 ===
−
 
 
 
<asy>
 
<asy>
 
size(150);
 
size(150);
Line 50: Line 49:
  
 
Hence <math>CE = FC + x = \frac{5}{2} \Rightarrow\boxed{\mathrm{(D)}\ \frac{5}{2}}</math>.
 
Hence <math>CE = FC + x = \frac{5}{2} \Rightarrow\boxed{\mathrm{(D)}\ \frac{5}{2}}</math>.
 +
 +
=== Solution 2 ===
 +
Call the point of tangency point <math>F</math> and the midpoint of <math>AB</math> as <math>G</math>. <math>CF=2</math> by Tangent Theorem. Notice that <math>\angle EGF=\frac{180-2\cdot\angle CGF}{2}=90-\angle CGF</math>. Thus, <math>\angle EGF=\angle FCG</math> and <math>\tan EGF=\tan FCG=\frac{1}{2}</math>. Solving <math>EF=\frac{1}{2}</math>. Adding, the answer is <math>\frac{5}{2}</math>.
 +
 +
=== Solution 3 ===
 +
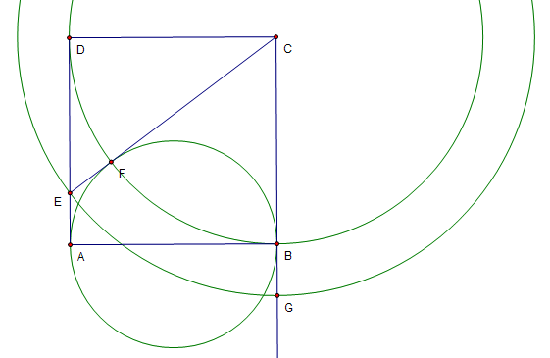
[[Image:2004_AMC12A-18.png]]
 +
 +
Clearly, <math>EA = EF = BG</math>. Thus, the sides of [[right triangle]] <math>CDE</math> are in arithmetic progression. Thus it is [[similar triangles|similar]] to the triangle <math>3 - 4 - 5</math> and since <math>DC = 2</math>, <math>CE = \frac{5}{2} \Rightarrow\boxed{\mathrm{(D)}\ \frac{5}{2}}</math>.
 +
 +
=== Solution 4 ===
 +
<asy>
 +
size(150);
 +
defaultpen(fontsize(10));
 +
pair A=(0,0), B=(2,0), C=(2,2), D=(0,2), E=(0,1/2), F=E+(C-E)/abs(C-E)/2, G=(1,0);
 +
draw(A--B--C--D--cycle);draw(C--E);
 +
draw(Arc((1,0),1,0,180));draw((A+B)/2--F);
 +
label("$A$",A,(-1,-1));
 +
label("$B$",B,( 1,-1));
 +
label("$C$",C,( 1, 1));
 +
label("$D$",D,(-1, 1));
 +
label("$E$",E,(-1, 0));
 +
label("$F$",F,( 0, 1));
 +
label("$x$",(A+E)/2,(-1, 0));
 +
label("$x$",(E+F)/2,( 0, 1));
 +
label("$2$",(F+C)/2,( 0, 1));
 +
label("$2$",(D+C)/2,( 0, 1));
 +
label("$2$",(B+C)/2,( 1, 0));
 +
label("$2-x$",(D+E)/2,(-1, 0));
 +
label("$G$",G,(0,-1));
 +
dot(G);
 +
draw(G--C);
 +
label("$\sqrt{5}$",(G+C)/2,(-1,0));
 +
</asy>
 +
 +
Let us call the midpoint of side <math>AB</math>, point <math>G</math>. Since the semicircle has radius 1, we can do the Pythagorean theorem on sides <math>GB, BC, GC</math>. We get <math>GC=\sqrt{5}</math>. We then know that <math>CF=2</math> by Pythagorean theorem. Then by connecting <math>EG</math>, we get similar triangles <math>EFG</math> and <math>GFC</math>. Solving the ratios, we get <math>x=\frac{1}{2}</math>, so the answer is <math> \frac{5}{2} \Rightarrow\boxed{\mathrm{(D)}\ \frac{5}{2}}</math>.
  
  
−
== Solution 2 ==
+
Alternatively, we could apply the Pythagorean theorem on triangle <math>CDE</math> to get the equation <cmath>(2-x)^2+2^2=(x+2)^2</cmath> which would give us that <math>x=\frac{1}{2}.</math> Adding up <math>CF</math> and <math>EF,</math> we get <math>2+\frac{1}{2}=\boxed{\mathrm{(D)}\ \frac{5}{2}}</math> again. Note that we know <math>DE=2-x</math> because <math> \triangle EFG\cong \triangle EAG</math> by <math>\text{HL.}</math>
  
−
[[Image:2004_AMC12A-18.png]]
+
~Alternate solution by Tinsel
 +
 
 +
=== Solution 5 ===
 +
Using the diagram as drawn in Solution 4, let the total area of square <math>ABCD</math> be divided into the triangles <math>DCE</math>, <math>EAG</math>, <math>CGB</math>, and <math>EGC</math>. Let x be the length of AE. Thus, the area of each triangle can be determined as follows:
 +
 
 +
<cmath>DCE = \frac{DC\cdot{DE}}{2} = \frac{2\cdot(2-x)}{2} = 2-x</cmath>
 +
 
 +
<cmath>EAG= \frac{AE\cdot{AG}}{2} = \frac{1\cdot{x}}{2} = \frac{x}{2}</cmath>
 +
 
 +
<cmath>CGB = \frac{GB\cdot{CB}}{2} = \frac{1\cdot(2)}{2} = 1</cmath>
 +
 
 +
<cmath>EGC= \frac{EG\cdot{GC}}{2} = \frac{\sqrt{5x^2 + 5}}{2}</cmath> (the length of CE is calculated with the [[Pythagorean Theorem]], lines GE and
 +
CE are perpendicular by definition of tangent)
 +
 
 +
Adding up the areas and equating to the area of the total square <cmath>(2 \cdot 2=4)</cmath>, we get
 +
 
 +
<cmath>x = \frac{1}{2}</cmath>
 +
 
 +
So, <cmath>CE = 2 + \frac{1}{2} = 5/2</cmath>.
 +
 
 +
~Typo Fix by doulai1
  
−
Clearly, <math>EA = EF = BG</math>. Thus, the sides of [[right triangle]] <math>CDE</math> are in arithmetic progression. Thus it is [[similar triangles|similar]] to the triangle <math>3 - 4 - 5</math> and since <math>DC = 2</math>, <math>CE = 5/2</math>.
+
=== Video Solution ===
 +
https://youtu.be/pM0zICtH6Lg
  
−
== Solution 3 ==
+
Education, the Study of Everything
−
[[Image:2004_AMC12A-18.png]]
 
−
TBE
 
  
−
== See also ==
+
== See Also ==
−
* [http://www.artofproblemsolving.com/Forum/viewtopic.php?t=131334 AoPS topic]
 
 
{{AMC12 box|year=2004|ab=A|num-b=17|num-a=19}}
 
{{AMC12 box|year=2004|ab=A|num-b=17|num-a=19}}
 +
 
{{AMC10 box|year=2004|ab=A|num-b=21|num-a=23}}
 
{{AMC10 box|year=2004|ab=A|num-b=21|num-a=23}}
−
 
−
[[Category:Intermediate Geometry Problems]]
 
 
{{MAA Notice}}
 
{{MAA Notice}}

Latest revision as of 14:30, 27 June 2024

The following problem is from both the 2004 AMC 12A #18 and 2004 AMC 10A #22, so both problems redirect to this page.

Problem

Square $ABCD$ has side length $2$. A semicircle with diameter $\overline{AB}$ is constructed inside the square, and the tangent to the semicircle from $C$ intersects side $\overline{AD}$ at $E$. What is the length of $\overline{CE}$?

[asy] size(100); defaultpen(fontsize(10)); pair A=(0,0), B=(2,0), C=(2,2), D=(0,2), E=(0,1/2); draw(A--B--C--D--cycle);draw(C--E); draw(Arc((1,0),1,0,180)); label("$A$",A,(-1,-1)); label("$B$",B,( 1,-1)); label("$C$",C,( 1, 1)); label("$D$",D,(-1, 1)); label("$E$",E,(-1, 0)); [/asy]

$\mathrm{(A) \ } \frac{2+\sqrt{5}}{2} \qquad \mathrm{(B) \ } \sqrt{5} \qquad \mathrm{(C) \ } \sqrt{6} \qquad \mathrm{(D) \ } \frac{5}{2} \qquad \mathrm{(E) \ } 5-\sqrt{5}$

Solutions

Solution 1

[asy] size(150); defaultpen(fontsize(10)); pair A=(0,0), B=(2,0), C=(2,2), D=(0,2), E=(0,1/2), F=E+(C-E)/abs(C-E)/2; draw(A--B--C--D--cycle);draw(C--E); draw(Arc((1,0),1,0,180));draw((A+B)/2--F); label("$A$",A,(-1,-1)); label("$B$",B,( 1,-1)); label("$C$",C,( 1, 1)); label("$D$",D,(-1, 1)); label("$E$",E,(-1, 0)); label("$F$",F,( 0, 1)); label("$x$",(A+E)/2,(-1, 0)); label("$x$",(E+F)/2,( 0, 1)); label("$2$",(F+C)/2,( 0, 1)); label("$2$",(D+C)/2,( 0, 1)); label("$2$",(B+C)/2,( 1, 0)); label("$2-x$",(D+E)/2,(-1, 0)); [/asy] Let the point of tangency be $F$. By the Two Tangent Theorem $BC = FC = 2$ and $AE = EF = x$. Thus $DE = 2-x$. The Pythagorean Theorem on $\triangle CDE$ yields

\begin{align*} DE^2 + CD^2 &= CE^2\\ (2-x)^2 + 2^2 &= (2+x)^2\\ x^2 - 4x + 8 &= x^2 + 4x + 4\\ x &= \frac{1}{2}\end{align*}

Hence $CE = FC + x = \frac{5}{2} \Rightarrow\boxed{\mathrm{(D)}\ \frac{5}{2}}$.

Solution 2

Call the point of tangency point $F$ and the midpoint of $AB$ as $G$. $CF=2$ by Tangent Theorem. Notice that $\angle EGF=\frac{180-2\cdot\angle CGF}{2}=90-\angle CGF$. Thus, $\angle EGF=\angle FCG$ and $\tan EGF=\tan FCG=\frac{1}{2}$. Solving $EF=\frac{1}{2}$. Adding, the answer is $\frac{5}{2}$.

Solution 3

2004 AMC12A-18.png

Clearly, $EA = EF = BG$. Thus, the sides of right triangle $CDE$ are in arithmetic progression. Thus it is similar to the triangle $3 - 4 - 5$ and since $DC = 2$, $CE = \frac{5}{2} \Rightarrow\boxed{\mathrm{(D)}\ \frac{5}{2}}$.

Solution 4

[asy] size(150); defaultpen(fontsize(10)); pair A=(0,0), B=(2,0), C=(2,2), D=(0,2), E=(0,1/2), F=E+(C-E)/abs(C-E)/2, G=(1,0); draw(A--B--C--D--cycle);draw(C--E); draw(Arc((1,0),1,0,180));draw((A+B)/2--F); label("$A$",A,(-1,-1)); label("$B$",B,( 1,-1)); label("$C$",C,( 1, 1)); label("$D$",D,(-1, 1)); label("$E$",E,(-1, 0)); label("$F$",F,( 0, 1)); label("$x$",(A+E)/2,(-1, 0)); label("$x$",(E+F)/2,( 0, 1)); label("$2$",(F+C)/2,( 0, 1)); label("$2$",(D+C)/2,( 0, 1)); label("$2$",(B+C)/2,( 1, 0)); label("$2-x$",(D+E)/2,(-1, 0)); label("$G$",G,(0,-1)); dot(G); draw(G--C); label("$\sqrt{5}$",(G+C)/2,(-1,0)); [/asy]

Let us call the midpoint of side $AB$, point $G$. Since the semicircle has radius 1, we can do the Pythagorean theorem on sides $GB, BC, GC$. We get $GC=\sqrt{5}$. We then know that $CF=2$ by Pythagorean theorem. Then by connecting $EG$, we get similar triangles $EFG$ and $GFC$. Solving the ratios, we get $x=\frac{1}{2}$, so the answer is $\frac{5}{2} \Rightarrow\boxed{\mathrm{(D)}\ \frac{5}{2}}$.


Alternatively, we could apply the Pythagorean theorem on triangle $CDE$ to get the equation \[(2-x)^2+2^2=(x+2)^2\] which would give us that $x=\frac{1}{2}.$ Adding up $CF$ and $EF,$ we get $2+\frac{1}{2}=\boxed{\mathrm{(D)}\ \frac{5}{2}}$ again. Note that we know $DE=2-x$ because $\triangle EFG\cong \triangle EAG$ by $\text{HL.}$

~Alternate solution by Tinsel

Solution 5

Using the diagram as drawn in Solution 4, let the total area of square $ABCD$ be divided into the triangles $DCE$, $EAG$, $CGB$, and $EGC$. Let x be the length of AE. Thus, the area of each triangle can be determined as follows:

\[DCE = \frac{DC\cdot{DE}}{2} = \frac{2\cdot(2-x)}{2} = 2-x\]

\[EAG= \frac{AE\cdot{AG}}{2} = \frac{1\cdot{x}}{2} = \frac{x}{2}\]

\[CGB = \frac{GB\cdot{CB}}{2} = \frac{1\cdot(2)}{2} = 1\]

\[EGC= \frac{EG\cdot{GC}}{2} = \frac{\sqrt{5x^2 + 5}}{2}\] (the length of CE is calculated with the Pythagorean Theorem, lines GE and CE are perpendicular by definition of tangent)

Adding up the areas and equating to the area of the total square \[(2 \cdot 2=4)\], we get

\[x = \frac{1}{2}\]

So, \[CE = 2 + \frac{1}{2} = 5/2\].

~Typo Fix by doulai1

Video Solution

https://youtu.be/pM0zICtH6Lg

Education, the Study of Everything

See Also

2004 AMC 12A (Problems • Answer Key • Resources)
Preceded by
Problem 17 		Followed by
Problem 19
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions
2004 AMC 10A (Problems • Answer Key • Resources)
Preceded by
Problem 21 		Followed by
Problem 23
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2004_AMC_12A_Problems/Problem_18&oldid=221173"