Difference between revisions of "2015 AIME II Problems/Problem 15"
m (→Solution 2) |
m (→Solution 11 (Trig)) |
||
| (61 intermediate revisions by 21 users not shown) | |||
| Line 2: | Line 2: | ||
Circles <math>\mathcal{P}</math> and <math>\mathcal{Q}</math> have radii <math>1</math> and <math>4</math>, respectively, and are externally tangent at point <math>A</math>. Point <math>B</math> is on <math>\mathcal{P}</math> and point <math>C</math> is on <math>\mathcal{Q}</math> so that line <math>BC</math> is a common external tangent of the two circles. A line <math>\ell</math> through <math>A</math> intersects <math>\mathcal{P}</math> again at <math>D</math> and intersects <math>\mathcal{Q}</math> again at <math>E</math>. Points <math>B</math> and <math>C</math> lie on the same side of <math>\ell</math>, and the areas of <math>\triangle DBA</math> and <math>\triangle ACE</math> are equal. This common area is <math>\frac{m}{n}</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m+n</math>. | Circles <math>\mathcal{P}</math> and <math>\mathcal{Q}</math> have radii <math>1</math> and <math>4</math>, respectively, and are externally tangent at point <math>A</math>. Point <math>B</math> is on <math>\mathcal{P}</math> and point <math>C</math> is on <math>\mathcal{Q}</math> so that line <math>BC</math> is a common external tangent of the two circles. A line <math>\ell</math> through <math>A</math> intersects <math>\mathcal{P}</math> again at <math>D</math> and intersects <math>\mathcal{Q}</math> again at <math>E</math>. Points <math>B</math> and <math>C</math> lie on the same side of <math>\ell</math>, and the areas of <math>\triangle DBA</math> and <math>\triangle ACE</math> are equal. This common area is <math>\frac{m}{n}</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m+n</math>. | ||
| + | |||
| + | <asy> | ||
| + | import cse5; | ||
| + | pathpen=black; pointpen=black; | ||
| + | size(6cm); | ||
| + | |||
| + | pair E = IP(L((-.2476,1.9689),(0.8,1.6),-3,5.5),CR((4,4),4)), D = (-.2476,1.9689); | ||
| + | |||
| + | filldraw(D--(0.8,1.6)--(0,0)--cycle,gray(0.7)); | ||
| + | filldraw(E--(0.8,1.6)--(4,0)--cycle,gray(0.7)); | ||
| + | D(CR((0,1),1)); D(CR((4,4),4,150,390)); | ||
| + | D(L(MP("D",D(D),N),MP("A",D((0.8,1.6)),NE),1,5.5)); | ||
| + | D((-1.2,0)--MP("B",D((0,0)),S)--MP("C",D((4,0)),S)--(8,0)); | ||
| + | D(MP("E",E,N)); | ||
| + | </asy> | ||
==Hint== | ==Hint== | ||
| − | + | <math>[ABC] = \frac{1}{2}ab \text{sin} C</math> is your friend for a quick solve. If you know about homotheties, go ahead, but you'll still need to do quite a bit of computation. If you're completely lost and you have a lot of time left in your mocking of this AIME, go ahead and use analytic geometry. | |
| + | |||
| + | ==Solution 1 (guys trig is fast)== | ||
| + | Let <math>M</math> be the intersection of <math>\overline{BC}</math> and the common internal tangent of <math>\mathcal P</math> and <math>\mathcal Q.</math> We claim that <math>M</math> is the circumcenter of right <math>\triangle{ABC}.</math> Indeed, we have <math>AM = BM</math> and <math>BM = CM</math> by equal tangents to circles, and since <math>BM = CM, M</math> is the midpoint of <math>\overline{BC},</math> implying that <math>\angle{BAC} = 90.</math> Now draw <math>\overline{PA}, \overline{PB}, \overline{PM},</math> where <math>P</math> is the center of circle <math>\mathcal P.</math> Quadrilateral <math>PAMB</math> is cyclic, and by Pythagorean Theorem <math>PM = \sqrt{5},</math> so by Ptolemy on <math>PAMB</math> we have <cmath>AB \sqrt{5} = 2 \cdot 1 + 2 \cdot 1 = 4 \iff AB = \dfrac{4 \sqrt{5}}{5}.</cmath> Do the same thing on cyclic quadrilateral <math>QAMC</math> (where <math>Q</math> is the center of circle <math>\mathcal Q</math> and get <math>AC = \frac{8 \sqrt{5}}{5}.</math> | ||
| − | ==Solution | + | Let <math>\angle A = \angle{DAB}.</math> By Law of Sines, <math>BD = 2R \sin A = 2 \sin A.</math> Note that <math>\angle{D} = \angle{ABC}</math> from inscribed angles, so |
| + | <cmath>\begin{align*} | ||
| + | [ABD] &= \dfrac{1}{2} BD \cdot AB \cdot \sin{\angle B} \\ | ||
| + | &= \dfrac{1}{2} \cdot \dfrac{4 \sqrt{5}}{5} \cdot 2 \sin A \sin{\left(180 - \angle A - \angle D\right)} \\ | ||
| + | &= \dfrac{4 \sqrt{5}}{5} \cdot \sin A \cdot \sin{\left(\angle A + \angle D\right)} \\ | ||
| + | &= \dfrac{4 \sqrt{5}}{5} \cdot \sin A \cdot \left(\sin A \cos D + \cos A \sin D\right) \\ | ||
| + | &= \dfrac{4 \sqrt{5}}{5} \cdot \sin A \cdot \left(\sin A \cos{\angle{ABC}} + \cos A \sin{\angle{ABC}}\right) \\ | ||
| + | &= \dfrac{4 \sqrt{5}}{5} \cdot \sin A \cdot \left(\dfrac{\sqrt{5} \sin A}{5} + \dfrac{2 \sqrt{5} \cos A}{5}\right) \\ | ||
| + | &= \dfrac{4}{5} \cdot \sin A \left(\sin A + 2 \cos A\right) | ||
| + | \end{align*}</cmath> after angle addition identity. | ||
| + | |||
| + | Similarly, <math>\angle{EAC} = 90 - \angle A,</math> and by Law of Sines <math>CE = 8 \sin{\angle{EAC}} = 8 \cos A.</math> Note that <math>\angle{E} = \angle{ACB}</math> from inscribed angles, so | ||
| + | <cmath>\begin{align*} | ||
| + | [ACE] &= \dfrac{1}{2} AC \cdot CE \sin{\angle C} \\ | ||
| + | &= \dfrac{1}{2} \cdot \dfrac{8 \sqrt{5}}{5} \cdot 8 \cos A \sin{\left[180 - \left(90 - \angle A\right) - \angle E\right]} \\ | ||
| + | &= \dfrac{32 \sqrt{5}}{5} \cdot \cos A \sin{\left[\left(90 - \angle A\right) + \angle{ACB}\right]} \\ | ||
| + | &= \dfrac{32 \sqrt{5}}{5} \cdot \cos A \left(\dfrac{2 \sqrt{5} \cos A}{5} + \dfrac{\sqrt{5} \sin A}{5}\right) \\ | ||
| + | &= \dfrac{32}{5} \cdot \cos A \left(\sin A + 2 \cos A\right) | ||
| + | \end{align*}</cmath> after angle addition identity. | ||
| + | Setting the two areas equal, we get <cmath>\tan A = \frac{\sin A}{\cos A} = 8 \iff \sin A = \frac{8}{\sqrt{65}}, \cos A = \frac{1}{\sqrt{65}}</cmath> after Pythagorean Identity. Now plug back in and the common area is <math>\frac{64}{65} \iff \boxed{129}.</math> | ||
| + | |||
| + | ==Solution 2== | ||
<asy> | <asy> | ||
unitsize(35); | unitsize(35); | ||
| Line 17: | Line 56: | ||
dot(O_1);dot(O_2); | dot(O_1);dot(O_2); | ||
draw(rightanglemark(O_1,B,N,5));draw(rightanglemark(O_2,C,N,5));draw(C--L,dashed);draw(B--K,dashed);draw(C--Y);draw(B--X); | draw(rightanglemark(O_1,B,N,5));draw(rightanglemark(O_2,C,N,5));draw(C--L,dashed);draw(B--K,dashed);draw(C--Y);draw(B--X); | ||
| + | |||
</asy> | </asy> | ||
| − | Call <math>O_1</math> and <math>O_2</math> the centers of circles <math>\mathcal{P}</math> and <math>\mathcal{Q}</math>, respectively, and | + | Call <math>O_1</math> and <math>O_2</math> the centers of circles <math>\mathcal{P}</math> and <math>\mathcal{Q}</math>, respectively, and extend <math>CB</math> and <math>O_2O_1</math> to meet at point <math>N</math>. Call <math>K</math> and <math>L</math> the feet of the altitudes from <math>B</math> to <math>O_1N</math> and <math>C</math> to <math>O_2N</math>, respectively. Using the fact that <math>\triangle{O_1BN} \sim \triangle{O_2CN}</math> and setting <math>NO_1 = k</math>, we have that <math>\frac{k+5}{k} = \frac{4}{1} \implies k=\frac{5}{3}</math>. We can do some more length chasing using triangles similar to <math>O_1BN</math> to get that <math>AK = AL = \frac{24}{15}</math>, <math>BK = \frac{12}{15}</math>, and <math>CL = \frac{48}{15}</math>. Now, consider the circles <math>\mathcal{P}</math> and <math>\mathcal{Q}</math> on the coordinate plane, where <math>A</math> is the origin. If the line <math>\ell</math> through <math>A</math> intersects <math>\mathcal{P}</math> at <math>D</math> and <math>\mathcal{Q}</math> at <math>E</math> then <math>4 \cdot DA = AE</math>. To verify this, notice that <math>\triangle{AO_1D} \sim \triangle{EO_2A}</math> from the fact that both triangles are isosceles with <math>\angle{O_1AD} \cong \angle{O_2AE}</math>, which are corresponding angles. Since <math>O_2A = 4\cdot O_1A</math>, we can conclude that <math>4 \cdot DA = AE</math>. |
| − | Hence, we need to find the slope <math>m</math> of line <math>\ell</math> such that the perpendicular distance <math>n</math> from <math>B</math> to <math>AD</math> is four times the perpendicular distance <math>p</math> from <math>C</math> to <math>AE</math>. This will mean that the product of the bases and heights of triangles <math>ACE</math> and <math>DBA</math> will be equal, which in turn means that their areas will be equal. Let the line <math>\ell</math> have the equation <math>y = -mx \implies mx + y = 0</math> | + | Hence, we need to find the slope <math>m</math> of line <math>\ell</math> such that the perpendicular distance <math>n</math> from <math>B</math> to <math>AD</math> is four times the perpendicular distance <math>p</math> from <math>C</math> to <math>AE</math>. This will mean that the product of the bases and heights of triangles <math>ACE</math> and <math>DBA</math> will be equal, which in turn means that their areas will be equal. Let the line <math>\ell</math> have the equation <math>y = -mx \implies mx + y = 0</math>, and let <math>m</math> be a positive real number so that the negative slope of <math>\ell</math> is preserved. Setting <math>A = (0,0)</math>, the coordinates of <math>B</math> are <math>(x_B, y_B) = \left(\frac{-24}{15}, \frac{-12}{15}\right)</math>, and the coordinates of <math>C</math> are <math>(x_C, y_C) = \left(\frac{24}{15}, \frac{-48}{15}\right)</math>. Using the point-to-line distance formula and the condition <math>n = 4p</math>, we have <cmath>\frac{|mx_B + 1(y_B) + 0|}{\sqrt{m^2 + 1}} = \frac{4|mx_C + 1(y_C) + 0|}{\sqrt{m^2 + 1}}</cmath> <cmath>\implies |mx_B + y_B| = 4|mx_C + y_C| \implies \left|\frac{-24m}{15} + \frac{-12}{15}\right| = 4\left|\frac{24m}{15} + \frac{-48}{15}\right|.</cmath> If <math>m > 2</math>, then clearly <math>B</math> and <math>C</math> would not lie on the same side of <math>\ell</math>. Thus since <math>m > 0</math>, we must switch the signs of all terms in this equation when we get rid of the absolute value signs. We then have <cmath>\frac{6m}{15} + \frac{3}{15} = \frac{48}{15} - \frac{24m}{15} \implies 2m = 3 \implies m = \frac{3}{2}.</cmath> Thus, the equation of <math>\ell</math> is <math>y = -\frac{3}{2}x</math>. |
| − | Then we can find the coordinates of <math>D</math> by finding the point <math>(x,y)</math> other than <math>A = (0,0)</math> where the circle <math>\mathcal{P}</math> intersects <math>\ell</math>. <math>\mathcal{P}</math> can be represented with the equation <math>(x + 1)^2 + y^2 = 1</math>, and substituting <math>y = -\frac{3}{2}x</math> into this equation yields < | + | Then we can find the coordinates of <math>D</math> by finding the point <math>(x,y)</math> other than <math>A = (0,0)</math> where the circle <math>\mathcal{P}</math> intersects <math>\ell</math>. <math>\mathcal{P}</math> can be represented with the equation <math>(x + 1)^2 + y^2 = 1</math>, and substituting <math>y = -\frac{3}{2}x</math> into this equation yields <math>x = 0, -\frac{8}{13}</math> as solutions. Discarding <math>x = 0</math>, the <math>y</math>-coordinate of <math>D</math> is <math>-\frac{3}{2} \cdot -\frac{8}{13} = \frac{12}{13}</math>. The distance from <math>D</math> to <math>A</math> is then <math>\frac{4}{\sqrt{13}}.</math> The perpendicular distance from <math>B</math> to <math>AD</math> or the height of <math>\triangle{DBA}</math> is <math>\frac{|\frac{3}{2}\cdot\frac{-24}{15} + \frac{-12}{15} + 0|}{\sqrt{\frac{3}{2}^2 + 1}} = \frac{\frac{48}{15}}{\frac{\sqrt{13}}{2}} = \frac{32}{5\sqrt{13}}.</math> Finally, the common area is <math>\frac{1}{2}\left(\frac{32}{5\sqrt{13}} \cdot \frac{4}{\sqrt{13}}\right) = \frac{64}{65}</math>, and <math>m + n = 64 + 65 = \boxed{129}</math>. |
| − | ==Solution | + | ==Solution 3== |
| − | By homothety, we deduce that <math>AE = 4 AD</math>. (The proof can also be executed by similar triangles formed from dropping perpendiculars from the centers of <math>P</math> and <math>Q</math> to <math>l</math>.) Therefore, our equality of area condition, or the equality of base times height condition, reduces to the fact that the distance from <math>B</math> to <math>l</math> is four times that from <math>C</math> to <math>l</math>. Let the distance from <math>C</math> be <math>x</math> and the distance from <math>B</math> be <math>4x</math>. | + | By [[homothety]], we deduce that <math>AE = 4 AD</math>. (The proof can also be executed by similar triangles formed from dropping perpendiculars from the centers of <math>P</math> and <math>Q</math> to <math>l</math>.) Therefore, our equality of area condition, or the equality of base times height condition, reduces to the fact that the distance from <math>B</math> to <math>l</math> is four times that from <math>C</math> to <math>l</math>. Let the distance from <math>C</math> be <math>x</math> and the distance from <math>B</math> be <math>4x</math>. |
Let <math>P</math> and <math>Q</math> be the centers of their respective circles. Then dropping a perpendicular from <math>P</math> to <math>Q</math> creates a <math>3-4-5</math> right triangle, from which <math>BC = 4</math> and, if <math>\alpha = \angle{AQC}</math>, that <math>\cos \alpha = \dfrac{3}{5}</math>. Then <math>\angle{BPA} = 180^\circ - \alpha</math>, and the Law of Cosines on triangles <math>APB</math> and <math>AQC</math> gives <math>AB = \dfrac{4}{\sqrt{5}}</math> and <math>AC = \dfrac{8}{\sqrt{5}}.</math> | Let <math>P</math> and <math>Q</math> be the centers of their respective circles. Then dropping a perpendicular from <math>P</math> to <math>Q</math> creates a <math>3-4-5</math> right triangle, from which <math>BC = 4</math> and, if <math>\alpha = \angle{AQC}</math>, that <math>\cos \alpha = \dfrac{3}{5}</math>. Then <math>\angle{BPA} = 180^\circ - \alpha</math>, and the Law of Cosines on triangles <math>APB</math> and <math>AQC</math> gives <math>AB = \dfrac{4}{\sqrt{5}}</math> and <math>AC = \dfrac{8}{\sqrt{5}}.</math> | ||
Now, using the Pythagorean Theorem to express the length of the projection of <math>BC</math> onto line <math>l</math> gives | Now, using the Pythagorean Theorem to express the length of the projection of <math>BC</math> onto line <math>l</math> gives | ||
| − | <cmath>\sqrt{\frac{16}{5} - | + | <cmath>\sqrt{\frac{16}{5} - 16x^2} + \sqrt{\frac{64}{5} - x^2} = \sqrt{16 - 9x^2}.</cmath> |
Squaring and simplifying gives | Squaring and simplifying gives | ||
<cmath>\sqrt{\left(\frac{1}{5} - x^2\right)\left(\frac{64}{5} - x^2\right)} = x^2,</cmath> | <cmath>\sqrt{\left(\frac{1}{5} - x^2\right)\left(\frac{64}{5} - x^2\right)} = x^2,</cmath> | ||
| Line 43: | Line 83: | ||
<cmath>AD = \sqrt{BD^2 - (4x)^2} + \sqrt{AB^2 - (4x)^2} = \frac{4}{\sqrt{13}},</cmath> | <cmath>AD = \sqrt{BD^2 - (4x)^2} + \sqrt{AB^2 - (4x)^2} = \frac{4}{\sqrt{13}},</cmath> | ||
and so the common area is <math>\dfrac{1}{2} \cdot \frac{4}{\sqrt{13}} \cdot \frac{32}{5\sqrt{13}} = \frac{64}{65}.</math> The answer is <math>\boxed{129}.</math> | and so the common area is <math>\dfrac{1}{2} \cdot \frac{4}{\sqrt{13}} \cdot \frac{32}{5\sqrt{13}} = \frac{64}{65}.</math> The answer is <math>\boxed{129}.</math> | ||
| + | |||
| + | ==Alternate Path to x== | ||
| + | Call the intersection of lines <math>l</math> and <math>BC</math> <math>E</math>.You can use similar triangles to find that the distance from <math>B</math> to <math>E</math> is four times the distance from <math>C</math> to <math>E</math>. Then draw a perpendicular from <math>A</math> to <math>BC</math> and call the point <math>F</math>. <math>AF = \frac{8}{5}</math> and <math>FE = FC + CE = \frac{16}{5} + \frac{4}{3} = \frac{68}{15}</math>, so by the Pythagorean Theorem, <math>AE = \dfrac{20\sqrt{13}}{5}</math>. You can now use similar triangles to find that <math>x = \dfrac{8}{5\sqrt{13}}</math> and continue on like in solution 2. | ||
| + | |||
| + | ==Solution 4== | ||
| + | <math>DE</math> goes through <math>A</math>, the point of tangency of both circles. So <math>DE</math> intercepts equal arcs in circle <math>P</math> and <math>Q</math>: [[homothety]]. Hence, <math>AE=4AD</math>. We will use such similarity later. | ||
| + | |||
| + | The diagonal distance between the centers of the circles is <math>4+1=5</math>. The difference in heights is <math>4-1=3</math>. So <math>BC=\sqrt{5^2-3^2}=4</math>. | ||
| + | |||
| + | The triangle connecting the centers with a side parallel to <math>BC</math> is a <math>3-4-5</math> right triangle. Since <math>O_PA=1</math>, the height of <math>A</math> is <math>1+3/5=8/5</math>. Drop an altitude from <math>A</math> to <math>BC</math> and call it <math>I</math>: <math>IB=4/5</math> and <math>IC=4-4/5=32/5</math>. Since right <math>\triangle AIB\sim\triangle CIB</math>, <math>ABC</math> is a right triangle also; <math>IB:IA:IC</math> form a geometric progression <math>\times 2</math>. | ||
| + | |||
| + | |||
| + | Extend <math>BA</math> through <math>A</math> to a point <math>G</math> on the other side of <math>\circ Q</math>. By [[homothety]], <math>\triangle DAB\sim\triangle EAG</math>. By angle chasing <math>\triangle DAB</math> through right triangle <math>ABC</math>, we deduce that <math>\angle CEG</math> is a right angle. Since <math>ACEG</math> is cyclic, <math>\angle GAC</math> is also right. So <math>CG</math> is a diameter of <math>\circ G</math>. Because of this, <math>CG \perp BC</math>, the tangent line. <math>\triangle BCG</math> is right and <math>\triangle BCG\sim\triangle ABC\sim\triangle CAG</math>. | ||
| + | |||
| + | |||
| + | <math>AC=\sqrt{(8/5)^2+(16/5)^2}=8\sqrt{5}/5</math> so <math>AG=2AC=16\sqrt{5}/5</math> and <math>[\triangle CAG]=64/5</math>. | ||
| + | |||
| + | Since <math>[\triangle DAB]=[\triangle ACE]</math>, the common area is <math>[ACEG]/17</math>. <math>16[\triangle DAB]=[\triangle GAE]</math> because the triangles are similar with a ratio of <math>1:4</math>. So we only need to find <math>[\triangle CEG]</math> now. | ||
| + | |||
| + | |||
| + | Extend <math>DE</math> through <math>E</math> to intersect the tangent at <math>F</math>. Because <math>4DA=AE</math>, the altitude from <math>B</math> to <math>AD</math> is <math>4</math> times the height from <math>C</math> to <math>EA</math>. So <math>BC=3/4BF</math> and <math>BF=16/3</math>. We look at right triangle <math>\triangle AIF</math>. <math>IF=68/15</math> and <math>AI=8/5</math>. <math>\triangle AIF</math> is a <math>17-6-5\sqrt{13}</math> right triangle. Hypotenuse <math>AF</math> intersects <math>CG</math> at a point, we call it <math>H</math>. <math>CH=4/3\div 68/15\cdot 8/5=8/17</math>. So <math>HG=8-8/17=128/17</math>. | ||
| + | |||
| + | |||
| + | By [[Power of a Point Theorem|Power of a Point]], <math>CH\cdot HG=AH\cdot HE</math>. <math>AH=16/5\cdot 5\sqrt{13}/17=16\sqrt{13}/17.</math> So <math>HE=1024/289\cdot 17/(16\sqrt{13})=64/(17\sqrt{13})</math>. The height from <math>E</math> to <math>CG</math> is <math>17/(5\sqrt{13})\cdot 64/(17\sqrt{13})=64/65</math>. | ||
| + | |||
| + | |||
| + | Thus, <math>[\triangle CEG]=64/65\cdot 8\div 2=256/65</math>. The area of the whole cyclic quadrilateral is <math>64/5+256/65=(832+256)/65=1088/65</math>. Lastly, the common area is <math>1/17</math> the area of the quadrilateral, or <math>64/65</math>. So <math>64+65=\boxed{129}</math>. | ||
| + | |||
| + | ==Solution 5 (HARD computation)== | ||
| + | <asy> | ||
| + | unitsize(35); | ||
| + | draw(Circle((-1,0),1)); | ||
| + | draw(Circle((4,0),4)); | ||
| + | pair A,O_1, O_2, B,C,D,E,N,K,L,X,Y; | ||
| + | A=(0,0);O_1=(-1,0);O_2=(4,0);B=(-24/15,-12/15);D=(-8/13,12/13);E=(32/13,-48/13);C=(24/15,-48/15);N=extension(E,B,O_2,O_1);K=foot(B,O_1,N);L=foot(C,O_2,N);X=foot(B,A,D);Y=foot(C,E,A); | ||
| + | label("$A$",A,NE);label("$O_1$",O_1,NE);label("$O_2$",O_2,NE);label("$B$",B,SW);label("$C$",C,SW);label("$D$",D,NE);label("$E$",E,NE);label("$N$",N,W);label("$K$",(-24/15,0.2));label("$L$",(24/15,0.2));label("$n$",(-0.8,-0.12));label("$p$",((29/15,-48/15)));label("$\mathcal{P}$",(-1.6,1.1));label("$\mathcal{Q}$",(6,4)); | ||
| + | draw(A--B--D--cycle);draw(A--E--C--cycle);draw(C--N);draw(O_2--N);draw(O_1--B,dashed);draw(O_2--C,dashed); | ||
| + | dot(O_1);dot(O_2); | ||
| + | draw(rightanglemark(O_1,B,N,5));draw(rightanglemark(O_2,C,N,5)); | ||
| + | //draw(C--L,dashed);draw(B--K,dashed);draw(C--Y);draw(B--X); | ||
| + | path circle2 = Circle((4,0),4); | ||
| + | N = (-8/3,0); | ||
| + | pair X =rotate(180,O_2)*E; | ||
| + | pair Y = (8,0); | ||
| + | draw(X--Y,dashed); draw(E--Y,dashed);draw(E--X,dashed); draw(Y--C,dashed); draw(C--X,dashed); draw(O_2--Y); | ||
| + | dot("$X$", X, NE);dot("$Y$", Y, NE); | ||
| + | </asy> | ||
| + | |||
| + | Consider the homothety that takes triangle BDA onto CXY on the big circle, as plotted. Some hidden congruence angles are revealed which help reduce computation complexity. Just some angle chasing and straight forward trigs. Because <math>AE=XY</math> and <math>AE \parallel XY</math>, <math>XYE</math> is right angle. | ||
| + | |||
| + | First, <math>\frac{NO_1}{NO_1+5} = \frac{1}{4}</math>, so <math>NO_1=\frac{5}{3}</math>. And, | ||
| + | <cmath>\cos{\angle{AO_2C}}=\cos{2\angle{AYC}} = \frac{O_2C}{NO_1+5} = \frac{3}{5}</cmath> | ||
| + | <cmath>\sin{\angle{AYC}} = \sqrt{\dfrac{1-\cos{2\angle{AYC}}}{2}}=\frac{1}{\sqrt{5}}</cmath> | ||
| + | <cmath> \cos{\angle{AYC}} = \frac{2}{\sqrt{5}}</cmath> | ||
| + | Then, | ||
| + | <cmath>[AEC] = \frac{1}{2}AE*CE*\sin{\angle{ACE}}=\frac{1}{2}AE*8\sin{\angle{CYE}}*\frac{1}{\sqrt{5}}</cmath> | ||
| + | <cmath>[CXY] = \frac{1}{2}CX*XY*\sin{\angle{CXY}}=\frac{1}{2}*8\sin{\angle{XYC}}*XY*\sin{\angle{CAY}}</cmath> | ||
| + | Since <math>\angle{CAY} = 90 - \angle{AYC}</math>, <math>\angle{XYC} = 90 - \angle{CYE}</math>, <math>XY = AE</math>, we have | ||
| + | <cmath>[CXY] = \frac{1}{2}*8AE\cos{\angle{CYE}}*\cos{\angle{AYC}}=\frac{1}{2}*8AE\cos{\angle{CYE}}*\frac{2}{\sqrt{5}}</cmath> | ||
| + | Since <math>\triangle{CXY}</math> is four times in scale to <math>\triangle{AEC}</math>, their area ratio is 16. Divide the two equations for the two areas, we have | ||
| + | <cmath>\tan{\angle{CYE}} = \frac{1}{8}</cmath> | ||
| + | With this angle found, everything else just follows. | ||
| + | <cmath>\sin{\angle{CYE}} = \dfrac{\tan{\angle{CYE}}}{\sqrt{1+\tan^2{\angle{CYE}}}}=\dfrac{1}{\sqrt{65}}</cmath> | ||
| + | <cmath>\cos{\angle{CYE}} = \dfrac{8}{\sqrt{65}}</cmath> | ||
| + | <cmath>\sin{\angle{AYE}} = \sin({\angle{AYC}+\angle{CYE}} )= \frac{1}{\sqrt{5}}*\frac{8}{\sqrt{65}} + \frac{2}{\sqrt{5}}*\frac{1}{\sqrt{65}} = \frac{2}{\sqrt{13}}</cmath> | ||
| + | <cmath>AE = 8\sin{\angle{AYE}} = \frac{16}{\sqrt{13}}</cmath> | ||
| + | <cmath>[AEC] = \frac{1}{2}*8*\frac{16}{\sqrt{13}}*\dfrac{1}{\sqrt{65}}*\frac{1}{\sqrt{5}}=\frac{64}{65}</cmath> | ||
| + | |||
| + | ==Solution 6 (Simple computation)== | ||
| + | |||
| + | Let <math>K</math> be the intersection of <math>BC</math> and <math>AE</math>. Since the radii of the two circles are 1:4, so we have <math>AD:AE=1:4</math>, and the distance from <math>B</math> to line <math>l</math> and the distance from <math>C</math> to line <math>l</math> are in a ratio of 4:1, so <math>BK:CK=4:1</math>. We can easily calculate the length of <math>BC</math> to be 4, so <math>CK=\frac{4}{3}</math>. Let <math>J</math> be the foot of perpendicular line from <math>A</math> to <math>BC</math>, we can know that <math>BJ:CJ=1:4</math>, so <math>BJ = 0.8</math>, <math>CJ=3.2</math>, <math>AJ=1.6</math>, and <math>AK=\sqrt{1.6^2+\left(3.2+\frac{4}{3}\right)^2}=\frac{4}{3}\sqrt{13}</math>. Since <math>CK^2 = EK\cdot AK</math>, so <math>EK=\frac{4}{39}\sqrt{13}</math>, and <math>AE = \frac{4}{3}\sqrt{13} - \frac{4}{39}\sqrt{13}= \frac{16}{13}\sqrt{13}</math>. <math>\sin\angle AKB=\frac{AJ}{AK} = \frac{1.6}{\frac{4}{3}\sqrt{13}}=\frac{1.2}{\sqrt{13}}</math>, so the distance from <math>C</math> to line <math>l</math> is <math>d=CK\cdot \sin\angle AKB = \frac{4}{3}\cdot \frac{1.2}{\sqrt{13}}=\frac{1.6}{\sqrt{13}}</math>. so the area is | ||
| + | <cmath> | ||
| + | [ACE] = \frac{1}{2}\cdot AE\cdot d = \frac{1}{2}\cdot\frac{16}{13}\sqrt{13}\frac{1.6}{\sqrt{13}} = \frac{64}{65} | ||
| + | </cmath> | ||
| + | The final answer is <math>\boxed{129}</math>. | ||
| + | |||
| + | --- by Dan Li | ||
| + | |||
| + | ==Solution 7== | ||
| + | Consider the common tangent from <math>A</math> to both circles. Let this intersect <math>BC</math> at point <math>K</math>. From equal tangents, we have <math>BK=AK=CK</math>, which implies that <math>\angle BAC = 90^\circ</math>. | ||
| + | |||
| + | Let the center of <math>\mathcal{P}</math> be <math>O_1</math>, and the center of <math>\mathcal{Q}</math> be <math>O_2</math>. Angle chasing, we find that <math>\triangle O_1DA \sim \triangle O_2EA</math> with a ratio of <math>1:4</math>. Hence <math>4AD = AE</math>. | ||
| + | |||
| + | We can easily deduce that <math>BC=4</math> by dropping an altitude from <math>O_1</math> to <math>O_2C</math>. Let <math>\angle ABC = \theta</math>. By some simple angle chasing, we obtain that <math>\angle BO_1A = 2\angle BDA = 2\angle ABC = 2\theta,</math> and similarly <math>\angle CO_2A = 180 - 2\theta</math>. | ||
| + | |||
| + | Using LoC, we get that <math>AB = \sqrt{2-2\cos2\theta}</math> and <math>AC = \sqrt{32+32\cos2\theta}</math>. From Pythagorean theorem, we have <cmath>AB^2 + AC^2 = BC^2 \implies \cos 2\theta = -\frac{3}{5} \implies \cos \theta = \frac{1}{\sqrt5}, \sin \theta = \frac{2}{\sqrt 5}</cmath> | ||
| + | In other words, <math>AB = \frac{4}{\sqrt5}, AC = \frac{8}{\sqrt5}</math>. | ||
| + | |||
| + | Using the area condition, we have: | ||
| + | <cmath>\begin{align*} | ||
| + | \frac12 AD*AB \sin \angle DAB &= \frac 12 AE*AC \sin(90-\angle DAB) \\ | ||
| + | AD*\frac{4}{\sqrt5} \sin \angle DAB &= 4AD*\frac{8}{\sqrt5} \cos \angle DAB \\ | ||
| + | \sin \angle DAB &= 8 \cos \angle DAB \\ | ||
| + | \implies \sin \angle DAB &= \frac{8}{\sqrt{65}} | ||
| + | \end{align*}</cmath> | ||
| + | |||
| + | Now, for brevity, let <math>\angle D = \angle ADB</math> and <math>\angle A = \angle DAB</math>. | ||
| + | |||
| + | From Law of Sines on <math>\triangle ABD</math>, we have | ||
| + | <cmath>\begin{align*} | ||
| + | \frac{AB}{\sin \angle D} &= \frac{AD}{\sin (180-\angle A - \angle D)} \\ | ||
| + | \frac{\frac{4}{\sqrt5}}{\frac{2}{\sqrt5}} &= \frac{AD}{\sin \angle A \cos\angle D + \sin \angle D\cos\angle A} \\ | ||
| + | 2 &= \frac{AD}{\frac{2}{\sqrt{13}}} \\ | ||
| + | AD &= \frac{4}{\sqrt{13}} | ||
| + | \end{align*}</cmath> | ||
| + | |||
| + | It remains to find the area of <math>\triangle ABD</math>. This is just <cmath>\frac12 AD*AB*\sin \angle A = \frac12 * \frac{4}{\sqrt{13}}*\frac{4}{\sqrt5}*\frac{8}{\sqrt{65}} = \frac{64}{65}</cmath> for an answer of <math>\boxed{129}.</math> | ||
| + | |||
| + | This solution was brought to you by Leonard_my_dude. | ||
| + | |||
| + | ==Solution 8 (Synthetic-Trigonometry)== | ||
| + | Add in the line <math>k</math> as the internal tangent between the two circles. Let <math>M</math> be the midpoint of <math>BC</math>; It is well-known that <math>M</math> is on <math>k</math> and because <math>k</math> is the radical axis of the two circles, <math>AM=BM=CM</math>. Therefore because <math>M</math> is the circumcenter of <math>\triangle{BAC}</math>, <math>\angle{BAC}=90^{\circ}</math>. Let <math>O_P</math> be the center of circle <math>\mathcal{P}</math> and likewise let <math>O_Q</math> be the center of circle <math>\mathcal{Q}</math>. It is well known that by homothety <math>O_P, A,</math> and <math>O_Q</math> are collinear. It is well-known that <math>\angle{ABC}=\angle{ADB}=b</math>, and likewise <math>\angle{ACB}=\angle{AEC}=c</math>. By homothety, <math>AD=4AE</math>, therefore since the two triangles mentioned in the problem, the length of the altitude from <math>B</math> to <math>AD</math> is four times the length of the altitude from <math>C</math> to <math>AE</math>. Using the Pythagorean Theorem, <math>BC = 4</math>. By angle-chasing, <math>O_{P}AMB</math> is cyclic, and likewise <math>O_{Q}CMA</math> is cyclic. Use the Pythagorean Theorem for <math>\triangle{O_{P}BM}</math> to get <math>O_{P}M=\sqrt{5}</math>. Then by Ptolemy's Theorem <math>AB=\frac{4\sqrt{5}}{5} \implies AC=\frac{8\sqrt{5}}{5}</math>. Now to compute the area, using what we know about the length of the altitude from <math>B</math> to <math>AD</math> is four times the length of the altitude from <math>C</math> to <math>AE</math>, letting <math>x</math> be the length of the altitude from <math>C</math> to <math>AE</math>, <math>x=\frac{8}{5\sqrt{13}}</math>. From the Law of Sines, <math>\frac{BD}{\sin{A}}=2 \implies \sin{A}=\frac{4x}{AB} \implies BD=\frac{8x}{AB}=\frac{16\sqrt{65}}{65}</math>. Then use the Pythagorean Theorem twice and add up the lengths to get <math>AD=\frac{4}{\sqrt{13}}</math>. Use the formula <math>\frac{b \times h}{2}</math> to get <math>\frac{64}{65} = \boxed{129}</math> as the answer. | ||
| + | |||
| + | ~First | ||
| + | |||
| + | ==Solution 9 (Visual)== | ||
| + | [[File:2015 AIME II 15.png|400px|right]] | ||
| + | [[File:2015 AIME II 15a.png|400px|right]] | ||
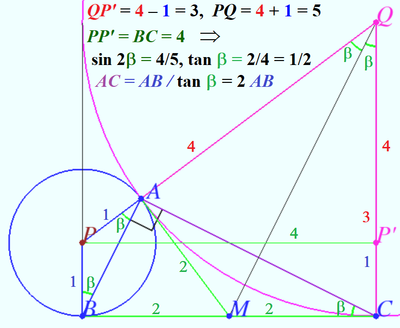
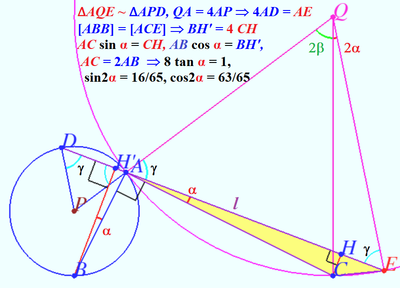
| + | Let <math>P</math> and <math>Q</math> be the centers of circles <math>\mathcal{P}</math> and <math>\mathcal{Q}</math> , respectively. | ||
| + | |||
| + | Let <math>M</math> be midpoint <math>BC, \beta = \angle ACB.</math> | ||
| + | |||
| + | Upper diagram shows that | ||
| + | |||
| + | <math>\sin 2\beta = \frac {4}{5}</math> and <math>AC = 2 AB.</math> Therefore <math>\cos 2\beta = \frac {3}{5}.</math> | ||
| + | |||
| + | Let <math>CH\perp l, BH'\perp l.</math> Lower diagram shows that | ||
| + | |||
| + | <math>\angle CAE = \angle ABH' = \alpha</math> (perpendicular sides) | ||
| + | |||
| + | and <math>\angle CQE = 2\alpha</math> (the same intersept <math>\overset{\Large\frown} {CE}).</math> | ||
| + | <cmath>\tan\alpha = \frac {1}{8}, | ||
| + | \sin2\alpha = \frac{2 \tan \alpha}{1 + \tan^2 \alpha} = \frac {16}{65}, | ||
| + | \cos2\alpha = \frac{1 - \tan^2 \alpha}{1 + \tan^2 \alpha} = \frac {63}{65}.</cmath> | ||
| + | The area | ||
| + | <cmath>[ACE] = [AQC]+[CQE]– [AQE].</cmath> | ||
| + | Hence <cmath>[ACE] =\frac{AQ^2}{2} \left(\sin 2\alpha + \sin 2\beta - \sin(2\alpha + 2\beta)\right),</cmath> | ||
| + | <cmath>[ACE] = | ||
| + | 8\left( \frac{16}{65}+\frac{4}{5} - \frac{4}{5}\cdot \frac{63}{65} - \frac{3}{5}\cdot \frac{16}{65}\right) = \frac{64}{65}\implies \boxed {129}.</cmath> | ||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Solution 10 (Similar Triangles, Angle Chasing, and Ptolemy's)== | ||
| + | We begin by extending <math>\overline{AB}</math> upwards until it intersects Circle <math>\mathcal{Q}</math>. We can call this point of intersection <math>F</math>. Connect <math>F</math> with <math>E</math>, <math>C</math>, and <math>A</math> for future use. | ||
| + | |||
| + | Create a trapezoid with points <math>B</math>, <math>C</math>, and the origins of Circles <math>\mathcal{P}</math> and <math>\mathcal{Q}</math>. After quick inspection, we can conclude that the distance between the origins is 5 and that <math>\overline{BC}</math> is 4. | ||
| + | |||
| + | (Note: It is important to understand that we could simply use the formula for the distance between the tangent points on a line and two different circles, which is <math>2\cdot \sqrt{a\cdot b}</math>, where <math>a</math> and <math>b</math> are the two respective radii of the circles. In our case, we get <math>2\cdot \sqrt{4} = 4</math>. | ||
| + | |||
| + | Using similar triangles or homotheties, <math>AE=4\cdot AD</math> and <math>AF=4\cdot BA</math>. <math>BC^2 = BA\cdot BF</math>. <cmath>16 = BA\cdot (5\cdot BA)</cmath> <cmath>BA = \frac{4}{\sqrt{5}}</cmath> <cmath>AF = \frac{16}{\sqrt{5}}</cmath> <cmath>BF = 4\cdot \sqrt{5}</cmath> | ||
| + | |||
| + | Inspecting <math>\triangle{BFC}</math>, we recognize that it is a right triangle (<math>\angle{BCF} = 90</math>) as the final length (<math>\overline{FC}</math>) being 8 would allow for an <math>x-2x-x\sqrt{5}</math> triangle. Hence, the diameter of circle <math>\mathcal{Q}</math> = <math>CF</math>. This also means that <math>\angle{CAF} = \angle{CEF} = 90</math>. | ||
| + | |||
| + | From the fact that <math>\triangle{ABC}</math> is a right triangle: <cmath>AB^2 + AC^2 = BC^2</cmath> <cmath>AC = \frac{8}{\sqrt{5}}</cmath> | ||
| + | (Note: We could have also used <math>\triangle{FAC}</math>.) | ||
| + | |||
| + | Our next step is to start angle chasing to find any other similar triangles or shared angles. Label the intersection between <math>\overline{FC}</math> and <math>\overline{DE}</math> as <math>M</math>. Label <math>\angle{CAE} = \angle{CFE} = \theta</math>. Since <math>\angle{BAC} = 90</math>, <math>\angle{EAF} = \angle{DAB} = 90-\theta</math>. Now, use the sine formula and the fact that the areas of <math>\triangle{DBA}</math> and <math>\triangle{ACE}</math> are equal to get: | ||
| + | <cmath>\frac{1}{2}\cdot AC\cdot AE\cdot \sin{\theta} = \frac{1}{2}\cdot AD\cdot AB\cdot \sin{(90-\theta)}</cmath> | ||
| + | Since <math>\sin{(90-\theta)} = \cos{\theta}</math>: | ||
| + | <cmath>\tan{\theta} = \frac{AD}{2\cdot AE}</cmath> | ||
| + | |||
| + | Using right <math>\triangle{FCE}</math>, since <math>\angle{ACM} = \angle{CFE}</math>, <math>\tan{\theta} = \frac{CE}{FE}</math>. Hence, plugging into the previous equation: | ||
| + | <cmath>\frac{CE}{FE} = \frac{AD}{2\cdot AE}</cmath> | ||
| + | Using the Pythagorean theorem on <math>\triangle{FCE}</math>, <math>FE = \sqrt{(64 - CE^2)}</math>. We also know that <math>AE=4\cdot AD</math> | ||
| + | Plugging back in: | ||
| + | <cmath>\frac{CE}{\sqrt{(64 - CE^2)}} = \frac{AD}{2\cdot (4\cdot AD)}</cmath> | ||
| + | <cmath>\frac{CE}{\sqrt{(64 - CE^2)}} = \frac{1}{8}</cmath>. | ||
| + | From here, we can square both sides and bring everything to one side to get: | ||
| + | <cmath>EF^2 + 64EF - 64 = 0</cmath>. | ||
| + | <cmath>EF = \frac{64}{\sqrt{65}}</cmath> | ||
| + | <cmath>CE = \frac{8}{\sqrt{65}}</cmath> | ||
| + | We should also return to the fact that <math>\sin{\theta} = \frac{CE}{CF}</math> from <math>\triangle{FCE}</math>, so <cmath>\sin{\theta} = \frac{1}{\sqrt{65}}</cmath> | ||
| + | |||
| + | From the fact that <math>\angle{CAF} = \angle{CEF} = 90</math>, we can use Ptolemy's Theorem on quadrilateral <math>ACEF</math>. <math>AC\cdot EF + CE\cdot FA = CF\cdot AE</math>. Plugging in and solving, we get that <math>AE = \frac{16}{\sqrt{13}}</math>. | ||
| + | |||
| + | We now have all of our pieces to use the Sine Formula on <math>\triangle{ACE}</math>. <cmath>\frac{1}{2}\cdot AC\cdot AF\cdot \sin{\theta}</cmath> | ||
| + | <cmath>\frac{1}{2}\cdot \frac{8}{\sqrt{5}}\cdot \frac{16}{\sqrt{13}}\cdot \frac{1}{\sqrt{65}} = \frac{64}{65} = \boxed {129}</cmath> | ||
| + | |||
| + | ~Solution by: armang32324 | ||
| + | |||
| + | ==Solution 11 (Trig)== | ||
| + | Let the center of the larger circle be <math>O,</math> and the center of the smaller circle be <math>P.</math> It is not hard to find the areas of <math>ACO</math> and <math>ABP</math> using pythagorean theorem, which are <math>\frac{32}{5}</math> and <math>\frac{2}{5}</math> respectively. Assign <math>\angle AOC=a,\angle COE=c,\angle DPB=d,\angle BPA=b.</math> We can figure out that <math>\angle AOE=\angle DOA=\theta</math> using vertical angles and isosceles triangles. Now, using <math>[ABC]=\frac{1}{2}ab\sin C</math> | ||
| + | <cmath>[ACE]=[AOC]+[COE]-[AOC]=\dfrac{32}{5}-8\sin c-8\sin \theta,</cmath> | ||
| + | <cmath>[DAB]=[APD]+[APB]+[BPD]=\dfrac{2}{5}+\dfrac{1}{2}\sin \theta+\dfrac{1}{2}\sin d.</cmath> | ||
| + | We can also figure out that <math>\sin a=\dfrac{4}{5},\cos a=\dfrac{3}{5},\sin b=\dfrac{4}{5}, \cos b=-\dfrac{3}{5}.</math> Also, <math>c=\theta-a</math> and <math>d=360-\theta-b.</math> Using sum and difference identities: | ||
| + | <cmath>\sin c=\dfrac{3}{5}\sin \theta-\dfrac{4}{5}\cos \theta,</cmath> | ||
| + | <cmath>\sin d=\dfrac{3}{5}\sin\theta-\dfrac{4}{5}\cos\theta.</cmath> | ||
| + | (We can also notice that <math>c+d=360-\theta-b+\theta-a=360-(a+b)=180</math> which means that <math>\sin c=\sin d.</math>) | ||
| + | Substituting in the equations for <math>\sin c</math> and <math>\sin d</math> into the equations for <math>[ACE]</math> and <math>[DAB],</math> setting them equal, and simplifying: | ||
| + | <cmath>3=2\sin\theta+3\cos\theta.</cmath> | ||
| + | Solving this equation we get that <math>\sin\theta=\frac{12}{13}</math> and <math>\cos\theta=\frac{5}{13}.</math> Doing a lot of substitution gives us <cmath>[ACE]=[DAB]=\dfrac{64}{65},</cmath> which means the answer is <math>64+65=\boxed{129}.</math> | ||
| + | |||
| + | ~[[BS2012]] | ||
| + | |||
| + | ==Video Solution== | ||
| + | https://youtu.be/LBCmQc2awMk | ||
| + | |||
| + | ~MathProblemSolvingSkills.com | ||
| + | |||
==See also== | ==See also== | ||
{{AIME box|year=2015|n=II|num-b=14|after=Last Problem}} | {{AIME box|year=2015|n=II|num-b=14|after=Last Problem}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Latest revision as of 18:15, 20 December 2023
Contents
- 1 Problem
- 2 Hint
- 3 Solution 1 (guys trig is fast)
- 4 Solution 2
- 5 Solution 3
- 6 Alternate Path to x
- 7 Solution 4
- 8 Solution 5 (HARD computation)
- 9 Solution 6 (Simple computation)
- 10 Solution 7
- 11 Solution 8 (Synthetic-Trigonometry)
- 12 Solution 9 (Visual)
- 13 Solution 10 (Similar Triangles, Angle Chasing, and Ptolemy's)
- 14 Solution 11 (Trig)
- 15 Video Solution
- 16 See also
Problem
Circles ![]() and
and ![]() have radii
have radii ![]() and
and ![]() , respectively, and are externally tangent at point
, respectively, and are externally tangent at point ![]() . Point
. Point ![]() is on
is on ![]() and point
and point ![]() is on
is on ![]() so that line
so that line ![]() is a common external tangent of the two circles. A line
is a common external tangent of the two circles. A line ![]() through
through ![]() intersects
intersects ![]() again at
again at ![]() and intersects
and intersects ![]() again at
again at ![]() . Points
. Points ![]() and
and ![]() lie on the same side of
lie on the same side of ![]() , and the areas of
, and the areas of ![]() and
and ![]() are equal. This common area is
are equal. This common area is ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
![[asy] import cse5; pathpen=black; pointpen=black; size(6cm); pair E = IP(L((-.2476,1.9689),(0.8,1.6),-3,5.5),CR((4,4),4)), D = (-.2476,1.9689); filldraw(D--(0.8,1.6)--(0,0)--cycle,gray(0.7)); filldraw(E--(0.8,1.6)--(4,0)--cycle,gray(0.7)); D(CR((0,1),1)); D(CR((4,4),4,150,390)); D(L(MP("D",D(D),N),MP("A",D((0.8,1.6)),NE),1,5.5)); D((-1.2,0)--MP("B",D((0,0)),S)--MP("C",D((4,0)),S)--(8,0)); D(MP("E",E,N)); [/asy]](http://latex.artofproblemsolving.com/6/b/7/6b7782afc839b219809c6266cec4abca23e9d026.png)
Hint
![]() is your friend for a quick solve. If you know about homotheties, go ahead, but you'll still need to do quite a bit of computation. If you're completely lost and you have a lot of time left in your mocking of this AIME, go ahead and use analytic geometry.
is your friend for a quick solve. If you know about homotheties, go ahead, but you'll still need to do quite a bit of computation. If you're completely lost and you have a lot of time left in your mocking of this AIME, go ahead and use analytic geometry.
Solution 1 (guys trig is fast)
Let ![]() be the intersection of
be the intersection of ![]() and the common internal tangent of
and the common internal tangent of ![]() and
and ![]() We claim that
We claim that ![]() is the circumcenter of right
is the circumcenter of right ![]() Indeed, we have
Indeed, we have ![]() and
and ![]() by equal tangents to circles, and since
by equal tangents to circles, and since ![]() is the midpoint of
is the midpoint of ![]() implying that
implying that ![]() Now draw
Now draw ![]() where
where ![]() is the center of circle
is the center of circle ![]() Quadrilateral
Quadrilateral ![]() is cyclic, and by Pythagorean Theorem
is cyclic, and by Pythagorean Theorem ![]() so by Ptolemy on
so by Ptolemy on ![]() we have
we have ![]() Do the same thing on cyclic quadrilateral
Do the same thing on cyclic quadrilateral ![]() (where
(where ![]() is the center of circle
is the center of circle ![]() and get
and get ![]()
Let ![]() By Law of Sines,
By Law of Sines, ![]() Note that
Note that ![]() from inscribed angles, so
from inscribed angles, so
![\begin{align*} [ABD] &= \dfrac{1}{2} BD \cdot AB \cdot \sin{\angle B} \\ &= \dfrac{1}{2} \cdot \dfrac{4 \sqrt{5}}{5} \cdot 2 \sin A \sin{\left(180 - \angle A - \angle D\right)} \\ &= \dfrac{4 \sqrt{5}}{5} \cdot \sin A \cdot \sin{\left(\angle A + \angle D\right)} \\ &= \dfrac{4 \sqrt{5}}{5} \cdot \sin A \cdot \left(\sin A \cos D + \cos A \sin D\right) \\ &= \dfrac{4 \sqrt{5}}{5} \cdot \sin A \cdot \left(\sin A \cos{\angle{ABC}} + \cos A \sin{\angle{ABC}}\right) \\ &= \dfrac{4 \sqrt{5}}{5} \cdot \sin A \cdot \left(\dfrac{\sqrt{5} \sin A}{5} + \dfrac{2 \sqrt{5} \cos A}{5}\right) \\ &= \dfrac{4}{5} \cdot \sin A \left(\sin A + 2 \cos A\right) \end{align*}](http://latex.artofproblemsolving.com/c/3/a/c3a05b76c76b1a9f0e7b0e6efd3502533396daff.png) after angle addition identity.
after angle addition identity.
Similarly, ![]() and by Law of Sines
and by Law of Sines ![]() Note that
Note that ![]() from inscribed angles, so
from inscribed angles, so
![\begin{align*} [ACE] &= \dfrac{1}{2} AC \cdot CE \sin{\angle C} \\ &= \dfrac{1}{2} \cdot \dfrac{8 \sqrt{5}}{5} \cdot 8 \cos A \sin{\left[180 - \left(90 - \angle A\right) - \angle E\right]} \\ &= \dfrac{32 \sqrt{5}}{5} \cdot \cos A \sin{\left[\left(90 - \angle A\right) + \angle{ACB}\right]} \\ &= \dfrac{32 \sqrt{5}}{5} \cdot \cos A \left(\dfrac{2 \sqrt{5} \cos A}{5} + \dfrac{\sqrt{5} \sin A}{5}\right) \\ &= \dfrac{32}{5} \cdot \cos A \left(\sin A + 2 \cos A\right) \end{align*}](http://latex.artofproblemsolving.com/c/2/4/c24fe39373ba10e834a5e13acdffe0caa1add903.png) after angle addition identity.
Setting the two areas equal, we get
after angle addition identity.
Setting the two areas equal, we get ![]() after Pythagorean Identity. Now plug back in and the common area is
after Pythagorean Identity. Now plug back in and the common area is ![]()
Solution 2
![[asy] unitsize(35); draw(Circle((-1,0),1)); draw(Circle((4,0),4)); pair A,O_1, O_2, B,C,D,E,N,K,L,X,Y; A=(0,0);O_1=(-1,0);O_2=(4,0);B=(-24/15,-12/15);D=(-8/13,12/13);E=(32/13,-48/13);C=(24/15,-48/15);N=extension(E,B,O_2,O_1);K=foot(B,O_1,N);L=foot(C,O_2,N);X=foot(B,A,D);Y=foot(C,E,A); label("$A$",A,NE);label("$O_1$",O_1,NE);label("$O_2$",O_2,NE);label("$B$",B,SW);label("$C$",C,SW);label("$D$",D,NE);label("$E$",E,NE);label("$N$",N,W);label("$K$",(-24/15,0.2));label("$L$",(24/15,0.2));label("$n$",(-0.8,-0.12));label("$p$",((29/15,-48/15)));label("$\mathcal{P}$",(-1.6,1.1));label("$\mathcal{Q}$",(6,4)); draw(A--B--D--cycle);draw(A--E--C--cycle);draw(C--N);draw(O_2--N);draw(O_1--B,dashed);draw(O_2--C,dashed); dot(O_1);dot(O_2); draw(rightanglemark(O_1,B,N,5));draw(rightanglemark(O_2,C,N,5));draw(C--L,dashed);draw(B--K,dashed);draw(C--Y);draw(B--X); [/asy]](http://latex.artofproblemsolving.com/a/7/8/a7802557b0402d026b6cf9218388bd0561ac27e4.png)
Call ![]() and
and ![]() the centers of circles
the centers of circles ![]() and
and ![]() , respectively, and extend
, respectively, and extend ![]() and
and ![]() to meet at point
to meet at point ![]() . Call
. Call ![]() and
and ![]() the feet of the altitudes from
the feet of the altitudes from ![]() to
to ![]() and
and ![]() to
to ![]() , respectively. Using the fact that
, respectively. Using the fact that ![]() and setting
and setting ![]() , we have that
, we have that ![]() . We can do some more length chasing using triangles similar to
. We can do some more length chasing using triangles similar to ![]() to get that
to get that ![]() ,
, ![]() , and
, and ![]() . Now, consider the circles
. Now, consider the circles ![]() and
and ![]() on the coordinate plane, where
on the coordinate plane, where ![]() is the origin. If the line
is the origin. If the line ![]() through
through ![]() intersects
intersects ![]() at
at ![]() and
and ![]() at
at ![]() then
then ![]() . To verify this, notice that
. To verify this, notice that ![]() from the fact that both triangles are isosceles with
from the fact that both triangles are isosceles with ![]() , which are corresponding angles. Since
, which are corresponding angles. Since ![]() , we can conclude that
, we can conclude that ![]() .
.
Hence, we need to find the slope ![]() of line
of line ![]() such that the perpendicular distance
such that the perpendicular distance ![]() from
from ![]() to
to ![]() is four times the perpendicular distance
is four times the perpendicular distance ![]() from
from ![]() to
to ![]() . This will mean that the product of the bases and heights of triangles
. This will mean that the product of the bases and heights of triangles ![]() and
and ![]() will be equal, which in turn means that their areas will be equal. Let the line
will be equal, which in turn means that their areas will be equal. Let the line ![]() have the equation
have the equation ![]() , and let
, and let ![]() be a positive real number so that the negative slope of
be a positive real number so that the negative slope of ![]() is preserved. Setting
is preserved. Setting ![]() , the coordinates of
, the coordinates of ![]() are
are ![]() , and the coordinates of
, and the coordinates of ![]() are
are ![]() . Using the point-to-line distance formula and the condition
. Using the point-to-line distance formula and the condition ![]() , we have
, we have ![]()
![]() If
If ![]() , then clearly
, then clearly ![]() and
and ![]() would not lie on the same side of
would not lie on the same side of ![]() . Thus since
. Thus since ![]() , we must switch the signs of all terms in this equation when we get rid of the absolute value signs. We then have
, we must switch the signs of all terms in this equation when we get rid of the absolute value signs. We then have ![]() Thus, the equation of
Thus, the equation of ![]() is
is ![]() .
.
Then we can find the coordinates of ![]() by finding the point
by finding the point ![]() other than
other than ![]() where the circle
where the circle ![]() intersects
intersects ![]() .
. ![]() can be represented with the equation
can be represented with the equation ![]() , and substituting
, and substituting ![]() into this equation yields
into this equation yields ![]() as solutions. Discarding
as solutions. Discarding ![]() , the
, the ![]() -coordinate of
-coordinate of ![]() is
is ![]() . The distance from
. The distance from ![]() to
to ![]() is then
is then ![]() The perpendicular distance from
The perpendicular distance from ![]() to
to ![]() or the height of
or the height of ![]() is
is  Finally, the common area is
Finally, the common area is ![]() , and
, and ![]() .
.
Solution 3
By homothety, we deduce that ![]() . (The proof can also be executed by similar triangles formed from dropping perpendiculars from the centers of
. (The proof can also be executed by similar triangles formed from dropping perpendiculars from the centers of ![]() and
and ![]() to
to ![]() .) Therefore, our equality of area condition, or the equality of base times height condition, reduces to the fact that the distance from
.) Therefore, our equality of area condition, or the equality of base times height condition, reduces to the fact that the distance from ![]() to
to ![]() is four times that from
is four times that from ![]() to
to ![]() . Let the distance from
. Let the distance from ![]() be
be ![]() and the distance from
and the distance from ![]() be
be ![]() .
.
Let ![]() and
and ![]() be the centers of their respective circles. Then dropping a perpendicular from
be the centers of their respective circles. Then dropping a perpendicular from ![]() to
to ![]() creates a
creates a ![]() right triangle, from which
right triangle, from which ![]() and, if
and, if ![]() , that
, that ![]() . Then
. Then ![]() , and the Law of Cosines on triangles
, and the Law of Cosines on triangles ![]() and
and ![]() gives
gives ![]() and
and ![]()
Now, using the Pythagorean Theorem to express the length of the projection of ![]() onto line
onto line ![]() gives
gives
![]() Squaring and simplifying gives
Squaring and simplifying gives
![\[\sqrt{\left(\frac{1}{5} - x^2\right)\left(\frac{64}{5} - x^2\right)} = x^2,\]](http://latex.artofproblemsolving.com/4/b/e/4be7cbd9d9e569e4adac0a37f5f01b4ab68a2b9f.png) and squaring and solving gives
and squaring and solving gives ![]()
By the Law of Sines on triangle ![]() , we have
, we have
![]() But we know
But we know ![]() , and so a small computation gives
, and so a small computation gives ![]() The Pythagorean Theorem now gives
The Pythagorean Theorem now gives
![]() and so the common area is
and so the common area is ![]() The answer is
The answer is ![]()
Alternate Path to x
Call the intersection of lines ![]() and
and ![]()
![]() .You can use similar triangles to find that the distance from
.You can use similar triangles to find that the distance from ![]() to
to ![]() is four times the distance from
is four times the distance from ![]() to
to ![]() . Then draw a perpendicular from
. Then draw a perpendicular from ![]() to
to ![]() and call the point
and call the point ![]() .
. ![]() and
and ![]() , so by the Pythagorean Theorem,
, so by the Pythagorean Theorem, ![]() . You can now use similar triangles to find that
. You can now use similar triangles to find that ![]() and continue on like in solution 2.
and continue on like in solution 2.
Solution 4
![]() goes through
goes through ![]() , the point of tangency of both circles. So
, the point of tangency of both circles. So ![]() intercepts equal arcs in circle
intercepts equal arcs in circle ![]() and
and ![]() : homothety. Hence,
: homothety. Hence, ![]() . We will use such similarity later.
. We will use such similarity later.
The diagonal distance between the centers of the circles is ![]() . The difference in heights is
. The difference in heights is ![]() . So
. So ![]() .
.
The triangle connecting the centers with a side parallel to ![]() is a
is a ![]() right triangle. Since
right triangle. Since ![]() , the height of
, the height of ![]() is
is ![]() . Drop an altitude from
. Drop an altitude from ![]() to
to ![]() and call it
and call it ![]() :
: ![]() and
and ![]() . Since right
. Since right ![]() ,
, ![]() is a right triangle also;
is a right triangle also; ![]() form a geometric progression
form a geometric progression ![]() .
.
Extend ![]() through
through ![]() to a point
to a point ![]() on the other side of
on the other side of ![]() . By homothety,
. By homothety, ![]() . By angle chasing
. By angle chasing ![]() through right triangle
through right triangle ![]() , we deduce that
, we deduce that ![]() is a right angle. Since
is a right angle. Since ![]() is cyclic,
is cyclic, ![]() is also right. So
is also right. So ![]() is a diameter of
is a diameter of ![]() . Because of this,
. Because of this, ![]() , the tangent line.
, the tangent line. ![]() is right and
is right and ![]() .
.
![]() so
so ![]() and
and ![]() .
.
Since ![]() , the common area is
, the common area is ![]() .
. ![]() because the triangles are similar with a ratio of
because the triangles are similar with a ratio of ![]() . So we only need to find
. So we only need to find ![]() now.
now.
Extend ![]() through
through ![]() to intersect the tangent at
to intersect the tangent at ![]() . Because
. Because ![]() , the altitude from
, the altitude from ![]() to
to ![]() is
is ![]() times the height from
times the height from ![]() to
to ![]() . So
. So ![]() and
and ![]() . We look at right triangle
. We look at right triangle ![]() .
. ![]() and
and ![]() .
. ![]() is a
is a ![]() right triangle. Hypotenuse
right triangle. Hypotenuse ![]() intersects
intersects ![]() at a point, we call it
at a point, we call it ![]() .
. ![]() . So
. So ![]() .
.
By Power of a Point, ![]() .
. ![]() So
So ![]() . The height from
. The height from ![]() to
to ![]() is
is ![]() .
.
Thus, ![]() . The area of the whole cyclic quadrilateral is
. The area of the whole cyclic quadrilateral is ![]() . Lastly, the common area is
. Lastly, the common area is ![]() the area of the quadrilateral, or
the area of the quadrilateral, or ![]() . So
. So ![]() .
.
Solution 5 (HARD computation)
![[asy] unitsize(35); draw(Circle((-1,0),1)); draw(Circle((4,0),4)); pair A,O_1, O_2, B,C,D,E,N,K,L,X,Y; A=(0,0);O_1=(-1,0);O_2=(4,0);B=(-24/15,-12/15);D=(-8/13,12/13);E=(32/13,-48/13);C=(24/15,-48/15);N=extension(E,B,O_2,O_1);K=foot(B,O_1,N);L=foot(C,O_2,N);X=foot(B,A,D);Y=foot(C,E,A); label("$A$",A,NE);label("$O_1$",O_1,NE);label("$O_2$",O_2,NE);label("$B$",B,SW);label("$C$",C,SW);label("$D$",D,NE);label("$E$",E,NE);label("$N$",N,W);label("$K$",(-24/15,0.2));label("$L$",(24/15,0.2));label("$n$",(-0.8,-0.12));label("$p$",((29/15,-48/15)));label("$\mathcal{P}$",(-1.6,1.1));label("$\mathcal{Q}$",(6,4)); draw(A--B--D--cycle);draw(A--E--C--cycle);draw(C--N);draw(O_2--N);draw(O_1--B,dashed);draw(O_2--C,dashed); dot(O_1);dot(O_2); draw(rightanglemark(O_1,B,N,5));draw(rightanglemark(O_2,C,N,5)); //draw(C--L,dashed);draw(B--K,dashed);draw(C--Y);draw(B--X); path circle2 = Circle((4,0),4); N = (-8/3,0); pair X =rotate(180,O_2)*E; pair Y = (8,0); draw(X--Y,dashed); draw(E--Y,dashed);draw(E--X,dashed); draw(Y--C,dashed); draw(C--X,dashed); draw(O_2--Y); dot("$X$", X, NE);dot("$Y$", Y, NE); [/asy]](http://latex.artofproblemsolving.com/8/8/f/88ff40209a59d89779ce1c7281eb1f46ed44526f.png)
Consider the homothety that takes triangle BDA onto CXY on the big circle, as plotted. Some hidden congruence angles are revealed which help reduce computation complexity. Just some angle chasing and straight forward trigs. Because ![]() and
and ![]() ,
, ![]() is right angle.
is right angle.
First, ![]() , so
, so ![]() . And,
. And,
![]()
![]()
![]() Then,
Then,
![]()
![]() Since
Since ![]() ,
, ![]() ,
, ![]() , we have
, we have
![]() Since
Since ![]() is four times in scale to
is four times in scale to ![]() , their area ratio is 16. Divide the two equations for the two areas, we have
, their area ratio is 16. Divide the two equations for the two areas, we have
![]() With this angle found, everything else just follows.
With this angle found, everything else just follows.
![]()
![]()
![]()
![]()
![]()
Solution 6 (Simple computation)
Let ![]() be the intersection of
be the intersection of ![]() and
and ![]() . Since the radii of the two circles are 1:4, so we have
. Since the radii of the two circles are 1:4, so we have ![]() , and the distance from
, and the distance from ![]() to line
to line ![]() and the distance from
and the distance from ![]() to line
to line ![]() are in a ratio of 4:1, so
are in a ratio of 4:1, so ![]() . We can easily calculate the length of
. We can easily calculate the length of ![]() to be 4, so
to be 4, so ![]() . Let
. Let ![]() be the foot of perpendicular line from
be the foot of perpendicular line from ![]() to
to ![]() , we can know that
, we can know that ![]() , so
, so ![]() ,
, ![]() ,
, ![]() , and
, and  . Since
. Since ![]() , so
, so ![]() , and
, and ![]() .
. ![]() , so the distance from
, so the distance from ![]() to line
to line ![]() is
is ![]() . so the area is
. so the area is
![]() The final answer is
The final answer is ![]() .
.
--- by Dan Li
Solution 7
Consider the common tangent from ![]() to both circles. Let this intersect
to both circles. Let this intersect ![]() at point
at point ![]() . From equal tangents, we have
. From equal tangents, we have ![]() , which implies that
, which implies that ![]() .
.
Let the center of ![]() be
be ![]() , and the center of
, and the center of ![]() be
be ![]() . Angle chasing, we find that
. Angle chasing, we find that ![]() with a ratio of
with a ratio of ![]() . Hence
. Hence ![]() .
.
We can easily deduce that ![]() by dropping an altitude from
by dropping an altitude from ![]() to
to ![]() . Let
. Let ![]() . By some simple angle chasing, we obtain that
. By some simple angle chasing, we obtain that ![]() and similarly
and similarly ![]() .
.
Using LoC, we get that ![]() and
and ![]() . From Pythagorean theorem, we have
. From Pythagorean theorem, we have ![]() In other words,
In other words, ![]() .
.
Using the area condition, we have:

Now, for brevity, let ![]() and
and ![]() .
.
From Law of Sines on ![]() , we have
, we have

It remains to find the area of ![]() . This is just
. This is just ![]() for an answer of
for an answer of ![]()
This solution was brought to you by Leonard_my_dude.
Solution 8 (Synthetic-Trigonometry)
Add in the line ![]() as the internal tangent between the two circles. Let
as the internal tangent between the two circles. Let ![]() be the midpoint of
be the midpoint of ![]() ; It is well-known that
; It is well-known that ![]() is on
is on ![]() and because
and because ![]() is the radical axis of the two circles,
is the radical axis of the two circles, ![]() . Therefore because
. Therefore because ![]() is the circumcenter of
is the circumcenter of ![]() ,
, ![]() . Let
. Let ![]() be the center of circle
be the center of circle ![]() and likewise let
and likewise let ![]() be the center of circle
be the center of circle ![]() . It is well known that by homothety
. It is well known that by homothety ![]() and
and ![]() are collinear. It is well-known that
are collinear. It is well-known that ![]() , and likewise
, and likewise ![]() . By homothety,
. By homothety, ![]() , therefore since the two triangles mentioned in the problem, the length of the altitude from
, therefore since the two triangles mentioned in the problem, the length of the altitude from ![]() to
to ![]() is four times the length of the altitude from
is four times the length of the altitude from ![]() to
to ![]() . Using the Pythagorean Theorem,
. Using the Pythagorean Theorem, ![]() . By angle-chasing,
. By angle-chasing, ![]() is cyclic, and likewise
is cyclic, and likewise ![]() is cyclic. Use the Pythagorean Theorem for
is cyclic. Use the Pythagorean Theorem for ![]() to get
to get ![]() . Then by Ptolemy's Theorem
. Then by Ptolemy's Theorem ![]() . Now to compute the area, using what we know about the length of the altitude from
. Now to compute the area, using what we know about the length of the altitude from ![]() to
to ![]() is four times the length of the altitude from
is four times the length of the altitude from ![]() to
to ![]() , letting
, letting ![]() be the length of the altitude from
be the length of the altitude from ![]() to
to ![]() ,
, ![]() . From the Law of Sines,
. From the Law of Sines, ![]() . Then use the Pythagorean Theorem twice and add up the lengths to get
. Then use the Pythagorean Theorem twice and add up the lengths to get ![]() . Use the formula
. Use the formula ![]() to get
to get ![]() as the answer.
as the answer.
~First
Solution 9 (Visual)
Let ![]() and
and ![]() be the centers of circles
be the centers of circles ![]() and
and ![]() , respectively.
, respectively.
Let ![]() be midpoint
be midpoint ![]()
Upper diagram shows that
![]() and
and ![]() Therefore
Therefore ![]()
Let ![]() Lower diagram shows that
Lower diagram shows that
![]() (perpendicular sides)
(perpendicular sides)
and ![]() (the same intersept
(the same intersept ![]()
![]() The area
The area
![]() Hence
Hence ![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Solution 10 (Similar Triangles, Angle Chasing, and Ptolemy's)
We begin by extending ![]() upwards until it intersects Circle
upwards until it intersects Circle ![]() . We can call this point of intersection
. We can call this point of intersection ![]() . Connect
. Connect ![]() with
with ![]() ,
, ![]() , and
, and ![]() for future use.
for future use.
Create a trapezoid with points ![]() ,
, ![]() , and the origins of Circles
, and the origins of Circles ![]() and
and ![]() . After quick inspection, we can conclude that the distance between the origins is 5 and that
. After quick inspection, we can conclude that the distance between the origins is 5 and that ![]() is 4.
is 4.
(Note: It is important to understand that we could simply use the formula for the distance between the tangent points on a line and two different circles, which is ![]() , where
, where ![]() and
and ![]() are the two respective radii of the circles. In our case, we get
are the two respective radii of the circles. In our case, we get ![]() .
.
Using similar triangles or homotheties, ![]() and
and ![]() .
. ![]() .
. ![]()
![]()
![]()
![]()
Inspecting ![]() , we recognize that it is a right triangle (
, we recognize that it is a right triangle (![]() ) as the final length (
) as the final length (![]() ) being 8 would allow for an
) being 8 would allow for an ![]() triangle. Hence, the diameter of circle
triangle. Hence, the diameter of circle ![]() =
= ![]() . This also means that
. This also means that ![]() .
.
From the fact that ![]() is a right triangle:
is a right triangle: ![]()
![]() (Note: We could have also used
(Note: We could have also used ![]() .)
.)
Our next step is to start angle chasing to find any other similar triangles or shared angles. Label the intersection between ![]() and
and ![]() as
as ![]() . Label
. Label ![]() . Since
. Since ![]() ,
, ![]() . Now, use the sine formula and the fact that the areas of
. Now, use the sine formula and the fact that the areas of ![]() and
and ![]() are equal to get:
are equal to get:
![]() Since
Since ![]() :
:
![]()
Using right ![]() , since
, since ![]() ,
, ![]() . Hence, plugging into the previous equation:
. Hence, plugging into the previous equation:
![]() Using the Pythagorean theorem on
Using the Pythagorean theorem on ![]() ,
, ![]() . We also know that
. We also know that ![]() Plugging back in:
Plugging back in:
![]()
![]() .
From here, we can square both sides and bring everything to one side to get:
.
From here, we can square both sides and bring everything to one side to get:
![]() .
.
![]()
![]() We should also return to the fact that
We should also return to the fact that ![]() from
from ![]() , so
, so ![]()
From the fact that ![]() , we can use Ptolemy's Theorem on quadrilateral
, we can use Ptolemy's Theorem on quadrilateral ![]() .
. ![]() . Plugging in and solving, we get that
. Plugging in and solving, we get that ![]() .
.
We now have all of our pieces to use the Sine Formula on ![]() .
. ![]()
![]()
~Solution by: armang32324
Solution 11 (Trig)
Let the center of the larger circle be ![]() and the center of the smaller circle be
and the center of the smaller circle be ![]() It is not hard to find the areas of
It is not hard to find the areas of ![]() and
and ![]() using pythagorean theorem, which are
using pythagorean theorem, which are ![]() and
and ![]() respectively. Assign
respectively. Assign ![]() We can figure out that
We can figure out that ![]() using vertical angles and isosceles triangles. Now, using
using vertical angles and isosceles triangles. Now, using ![]()
![]()
![]() We can also figure out that
We can also figure out that ![]() Also,
Also, ![]() and
and ![]() Using sum and difference identities:
Using sum and difference identities:
![]()
![]() (We can also notice that
(We can also notice that ![]() which means that
which means that ![]() )
Substituting in the equations for
)
Substituting in the equations for ![]() and
and ![]() into the equations for
into the equations for ![]() and
and ![]() setting them equal, and simplifying:
setting them equal, and simplifying:
![]() Solving this equation we get that
Solving this equation we get that ![]() and
and ![]() Doing a lot of substitution gives us
Doing a lot of substitution gives us ![]() which means the answer is
which means the answer is ![]()
Video Solution
~MathProblemSolvingSkills.com
See also
| 2015 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Problem | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.