Difference between revisions of "2011 AIME II Problems/Problem 10"

Latest revision as of 15:35, 24 November 2024

Problem 10

A circle with center $O$ has radius 25. Chord $\overline{AB}$ of length 30 and chord $\overline{CD}$ of length 14 intersect at point $P$ . The distance between the midpoints of the two chords is 12. The quantity $OP^2$ can be represented as $\frac{m}{n}$ , where $m$ and $n$ are relatively prime positive integers. Find the remainder when $m + n$ is divided by 1000.

Solution 1

Let $E$ and $F$ be the midpoints of $\overline{AB}$ and $\overline{CD}$ , respectively, such that $\overline{BE}$ intersects $\overline{CF}$ .

Since $E$ and $F$ are midpoints, $BE = 15$ and $CF = 7$ .

$B$ and $C$ are located on the circumference of the circle, so $OB = OC = 25$ .

The line through the midpoint of a chord of a circle and the center of that circle is perpendicular to that chord, so $\triangle OEB$ and $\triangle OFC$ are right triangles (with $\angle OEB$ and $\angle OFC$ being the right angles). By the Pythagorean Theorem, $OE = \sqrt{25^2 - 15^2} = 20$ , and $OF = \sqrt{25^2 - 7^2} = 24$ .

Let $x$ , $a$ , and $b$ be lengths $OP$ , $EP$ , and $FP$ , respectively. OEP and OFP are also right triangles, so $x^2 = a^2 + 20^2 \to a^2 = x^2 - 400$ , and $x^2 = b^2 + 24^2 \to b^2 = x^2 - 576$

We are given that $EF$ has length 12, so, using the Law of Cosines with $\triangle EPF$ :

$12^2 = a^2 + b^2 - 2ab \cos (\angle EPF) = a^2 + b^2 - 2ab \cos (\angle EPO + \angle FPO)$

Substituting for $a$ and $b$ , and applying the Cosine of Sum formula:

$144 = (x^2 - 400) + (x^2 - 576) - 2 \sqrt{x^2 - 400} \sqrt{x^2 - 576} \left( \cos \angle EPO \cos \angle FPO - \sin \angle EPO \sin \angle FPO \right)$

$\angle EPO$ and $\angle FPO$ are acute angles in right triangles, so substitute opposite/hypotenuse for sines and adjacent/hypotenuse for cosines:

$144 = 2x^2 - 976 - 2 \sqrt{(x^2 - 400)(x^2 - 576)} \left(\frac{\sqrt{x^2 - 400}}{x} \frac{\sqrt{x^2 - 576}}{x} - \frac{20}{x} \frac{24}{x} \right)$

Combine terms and multiply both sides by $x^2$ : $144 x^2 = 2 x^4 - 976 x^2 - 2 (x^2 - 400) (x^2 - 576) + 960 \sqrt{(x^2 - 400)(x^2 - 576)}$

Combine terms again, and divide both sides by 64: $13 x^2 = 7200 - 15 \sqrt{x^4 - 976 x^2 + 230400}$

Square both sides: $169 x^4 - 187000 x^2 + 51,840,000 = 225 x^4 - 219600 x^2 + 51,840,000$

This reduces to $x^2 = \frac{4050}{7} = (OP)^2$ ; $4050 + 7 \equiv \boxed{057} \pmod{1000}$ .

Solution 2 - Fastest

We begin as in the first solution. Once we see that $\triangle EOF$ has side lengths $12$ , $20$ , and $24$ , we can compute its area with Heron's formula:

$K = \sqrt{s(s-a)(s-b)(s-c)} = \sqrt{28\cdot 16\cdot 8\cdot 4} = 32\sqrt{14}.$

Thus, the circumradius of triangle $\triangle EOF$ is $R = \frac{abc}{4K} = \frac{45}{\sqrt{14}}$ . Looking at $EPFO$ , we see that $\angle OEP = \angle OFP = 90^\circ$ , which makes it a cyclic quadrilateral. This means $\triangle EOF$ 's circumcircle and $EPFO$ 's inscribed circle are the same.

Since $EPFO$ is cyclic with diameter $OP$ , we have $OP = 2R = \frac{90}{\sqrt{14}}$ , so $OP^2 = \frac{4050}{7}$ and the answer is $\boxed{057}$ .

Solution 3

We begin as the first solution have $OE=20$ and $OF=24$ . Because $\angle PEF+\angle PFO=180^{\circ}$ , Quadrilateral $EPFO$ is inscribed in a Circle. Assume point $I$ is the center of this circle.

$\because \angle OEP=90^{\circ}$

$\therefore$ point $I$ is on $OP$

Link $EI$ and $FI$ , Made line $IK\bot EF$ , then $\angle EIK=\angle EOF$

On the other hand, $\cos\angle EOF=\frac{EO^2+OF^2-EF^2}{2\cdot EO\cdot OF}=\frac{13}{15}=\cos\angle EIK$

$\sin\angle EOF=\sin\angle EIK=\sqrt{1-\frac{13^2}{15^2}}=\frac{2\sqrt{14}}{15}$

As a result, $IE=IO=\frac{45}{\sqrt 14}$

Therefore, $OP^2=4\cdot \frac{45^2}{14}=\frac{4050}{7}.$

As a result, $m+n=4057\equiv \boxed{057}\pmod{1000}$

Solution 4

Let $OP=x$ .

Proceed as the first solution in finding that quadrilateral $EPFO$ has side lengths $OE=20$ , $OF=24$ , $EP=\sqrt{x^2-20^2}$ , and $PF=\sqrt{x^2-24^2}$ , and diagonals $OP=x$ and $EF=12$ .

We note that quadrilateral $EPFO$ is cyclic and use Ptolemy's theorem to solve for $x$ :

$20\cdot \sqrt{x^2-24^2} + 12\cdot x = 24\cdot \sqrt{x^2-20^2}$

Solving, we have $x^2=\frac{4050}{7}$ so the answer is $\boxed{057}$ .

-Solution by blueberrieejam

~bluesoul changes the equation to a right equation, the previous equation isn't solvable

Solution 5 (Quick Angle Solution)

Let $M$ be the midpoint of $AB$ and $N$ of $CD$ . As $\angle OMP = \angle ONP$ , quadrilateral $OMPN$ is cyclic with diameter $OP$ . By Cyclic quadrilaterals note that $\angle MPO = \angle MNO$ .

The area of $\triangle MNP$ can be computed by Herons as $[MNO] = \sqrt{s(s-a)(s-b)(s-c)} = \sqrt{28\cdot 16\cdot 8\cdot 4} = 32\sqrt{14}.$ The area is also $\frac{1}{2}ON \cdot MN \sin{\angle MNO}$ . Therefore, $\begin{align*} \sin{\angle MNO} &= \frac{2[MNO]}{ON \cdot MN} \\ &= \frac{2}{9}\sqrt{14} \\ \sin{\angle MNO} &= \frac{OM}{OP} \\ &= \frac{2}{9}\sqrt{14} \\ OP &= \frac{90\sqrt{14}}{14} \\ OP^2 &= \frac{4050}{7} \implies \boxed{057}. \end{align*}$

~ Aaryabhatta1

Solution 6

Define $M$ and $N$ as the midpoints of $AB$ and $CD$ , respectively. Because $\angle OMP = \angle ONP = 90^{\circ}$ , we have that $ONPM$ is a cyclic quadrilateral. Hence, $\angle PNM = \angle POM.$ Then, let these two angles be denoted as $\alpha$ . Now, assume WLOG that $PD = x < 7$ and $PB = y < 15$ (We can do this because one of $PD$ or $PC$ must be less than 7, and similarly for $PB$ and $PA$ ). Then, by Power of a Point on P with respect to the circle with center $O$ , we have that $(14-x)x = (30-y)y$ $(7-x)^{2}+176=(15-y)^{2}.$ Then, let $z = (7-x)^{2}$ . From Law of Cosines on $\triangle NMP$ , we have that $\textrm{cos } \angle MNP = \frac{NP^{2}+MN^{2}-MP^{2}}{2 \cdot NP \cdot MN}$ $\textrm{cos } \alpha = \frac{(7-x)^{2} + 12^{2} - (14-x)^{2}}{24 \cdot (7-x)}.$ Plugging in $z$ in gives $\textrm{cos } \alpha = \frac{-32}{24 \cdot \sqrt{z}}$ $\textrm{cos } \alpha = \frac{-4}{3\sqrt{z}}$ $\textrm{cos }^{2} \alpha = \frac{16}{9z}.$ Hence, $\textrm{tan }^{2} \alpha = \frac{\frac{9z-16}{9z}}{\frac{16}{9z}} = \frac{9z-16}{16}.$ Then, we also know that $\textrm{tan } \alpha = \textrm{tan } \angle MOP = \frac{MP}{OM} = \frac{14-y}{20}.$ Squaring this, we get $\textrm{tan }^{2} \alpha = \frac{z+176}{400}.$ Equating our expressions for $z$ , we get $\frac{z+176}{400} = \frac{9z-16}{16}.$ Solving gives us that $z = \frac{18}{7}$ . Since $\angle ONP = 90^{\circ}$ , from the Pythagorean Theorem, $OP^{2} = ON^{2}+PN^{2} = 25^{2}-7^{2} + z = 576+z = \frac{4050}{7}$ , and thus the answer is $4050+7 = 4057$ , which when divided by a thousand leaves a remainder of $\boxed{57}.$

-Mr.Sharkman

Note: my solution was very long and tedious. It was definitely was the least elegant solution. The only thing I like about it is it contains no quadratic equations (unless you count LoC).

Solution 7 Analytic Geometry

Let $E$ and $F$ be the midpoints of $\overline{AB}$ and $\overline{CD}$ , respectively, such that $\overline{BE}$ intersects $\overline{CF}$ .

Since $E$ and $F$ are midpoints, $BE = 15$ and $CF = 7$ .

$B$ and $C$ are located on the circumference of the circle, so $OB = OC = 25$ .

Since $\overline{OE}\perp \overline{AB}$ and $\overline{OF}\perp \overline{CD}$ , $OE = \sqrt{OB^2-BE^2}=20$ and $OF = \sqrt{OC^2-OF^2}=24$

With law of cosines, $\cos \angle EOF = \frac{OE^2+OF^2-EF^2}{2\cdot OE\cdot OF} = \frac{13}{15}$

Since $EF < OF$ , $\angle EOF$ is acute angle. $\sin \angle EOF = \sqrt{1-\cos^2 \angle EOF} = \frac{\sqrt{56}}{15}$ and $\tan \angle EOF = \frac{\sqrt{56}}{13}$

Let $\overline{OF}$ line be $x$ axis.

Line $\overline{DC}$ equation is $x = OF$ .

Since line $\overline{AB}$ passes point $E$ and perpendicular to $\overline{OD}$ , its equation is $y - E_y = -\frac{1}{\tan \angle EOF} (x - E_x)$

where $E_x = OE\cos{\angle EOF}$ , $E_y = OE\sin{\angle EOF}$

Since $P$ is the intersection of $\overline{AB}$ and $\overline{CD}$ ,

$P_x = OF = 24$

$P_y = E_y -\frac{1}{\tan \angle EOF} (OF - E_x) = - \frac{3\sqrt{14}}{7}$ (Negative means point $P$ is between point $F$ and $C$ )

$OP^2 = P_x^2 + P_y^2 = \frac{4050}{7}$ and the answer is $\boxed{057}$ .

Note: if $EF$ was longer, point $P$ would be between point $D$ and $F$ . Then, $OP$ would be the diagonal of quadrilateral $OEPF$ not the side. To apply Ptolemy's theorem like solution 4, it is critical to know whether $OP$ is the diagonal or side of quadrilateral. Equation for wrong case cannot be solved. For example,

Solution 8 (Analytic- Can use complex numbers or rotation matrix)

$We work in the complex plane where $ O = 0 $. Let $ M_1, M_2 $, be midpoints of chords $ AB $, and $ CD $ respectively. $ AB=30 \rightarrow AM=15 $. Since $ AM=15 $, and $ OA=25 $, $ OM_1 = 20 $ by the Pythagorean theorem. WLOG, Let $ M_1 = 20 + 0i $. Think about the locus of all points $ M_2 $. By similar logic as above it is any $ M_2 $, such that $ OM_2=24 $. Note that $ M_1M_2 = 12 $. Therefore by LoC on $ \triangle OM_1M_2 $, if $ \angle O = \theta $, $ \cos\theta = \frac{13}{15} \rightarrow \sin\theta = \frac{2\sqrt{14}}{15} $. Note that a rotation by $ \theta $ and a scaling of $ \frac{24}{20} = \frac{6}{5} $ transforms $ AB $ to $ DC $. This transformation = $ \text{cis}\theta \cdot \frac{6}{5} = \frac{2}{5} \cdot \frac{13 + 2\sqrt{14}i}{5} $. Applying the transformation we on $ A,B $ respectively we find: (We are back in Cartesian coordinates now) \[ D = \frac{2}{5} \cdot (52 - 6\sqrt{14}, 39 + 8\sqrt{14}), \] \[ C = \frac{2}{5} \cdot (52 + 6\sqrt{14}, -39 + 8\sqrt{14}). \] To make bashing easier first ignore the $ \frac{2}{5} $. e.g. let $ D = 0.4D' $ and $ C = 0.4C' $ and first find the equation of the line passing through $ C' $ and $ D' $. After bashing a bit, we get \[ y = \frac{-13}{2\sqrt{14}} \cdot x + \frac{225}{7}\sqrt{14}. \] Now to account for the $ \frac{2}{5} $ thing we say the actual line is this: \[ y = \frac{-13}{2\sqrt{14}} \cdot x + \frac{2}{5} \cdot \frac{225}{7} \sqrt{14}, \] \[ y = \frac{-13}{2\sqrt{14}} \cdot x + \frac{90}{7} \sqrt{14}. \] $ P $ is the intersection of $ CD $ and $ AB $. We have the equation of $ CD $, and $ AB $ is simply $ x = 20 $, so Letting $ x = 20 $ we find \[ y = \frac{25\sqrt{14}}{7}. \] \[ OP^2 = 20^2 + \left( \frac{25\sqrt{14}}{7} \right)^2 = 5^2 \cdot \left( 4^2 + \left( \frac{5\sqrt{2}}{\sqrt{7}} \right)^2 \right) = 25 \cdot \frac{810}{7} = \frac{4050}{7}. \] Thus, the answer is $ \boxed{057} $.$

@@ Line 33: / Line 33: @@
 This reduces to <math>x^2 = \frac{4050}{7} = (OP)^2</math>; <math>4050 + 7 \equiv \boxed{057} \pmod{1000}</math>.
-==Solution 2==
+==Solution 2 - Fastest==
-We begin as in the first solution.  Once we see that <math>\triangle EPF</math> has side lengths 12,20, and 24, we can compute its area with Heron's formula:
+We begin as in the first solution.  Once we see that <math>\triangle EOF</math> has side lengths <math>12</math>, <math>20</math>, and <math>24</math>, we can compute its area with Heron's formula:
-<math>K = \sqrt{s(s-a)(s-b)(s-c)} = \sqrt{28\cdot 16\cdot 8\cdot 4} = 32\sqrt{14}</math>.
+<cmath>K = \sqrt{s(s-a)(s-b)(s-c)} = \sqrt{28\cdot 16\cdot 8\cdot 4} = 32\sqrt{14}.</cmath>
-So its circumradius is <math>R = \frac{abc}{4K} = \frac{45}{\sqrt{14}}</math>.  Since <math>EPFO</math> is [[cyclic]] with diameter <math>OP</math>, we have <math>OP = 2R = \frac{90}{\sqrt{14}}</math>, so <math>OP^2 = \frac{4050}{7}</math> and the answer is <math>\boxed{057}</math>.
+Thus, the circumradius of triangle <math>\triangle EOF</math> is <math>R = \frac{abc}{4K} = \frac{45}{\sqrt{14}}</math>.  Looking at <math>EPFO</math>, we see that <math>\angle OEP = \angle OFP = 90^\circ</math>, which makes it a cyclic quadrilateral. This means <math>\triangle EOF</math>'s circumcircle and <math>EPFO</math>'s inscribed circle are the same.
+Since <math>EPFO</math> is [[cyclic]] with diameter <math>OP</math>, we have <math>OP = 2R = \frac{90}{\sqrt{14}}</math>, so <math>OP^2 = \frac{4050}{7}</math> and the answer is <math>\boxed{057}</math>.
+==Solution 3==
+We begin as the first solution have <math>OE=20</math> and <math>OF=24</math>. Because <math>\angle PEF+\angle PFO=180^{\circ}</math>, Quadrilateral <math>EPFO</math> is inscribed in a Circle. Assume point <math>I</math> is the center of this circle.
+<math>\because \angle OEP=90^{\circ}</math>
+<math>\therefore</math> point <math>I</math> is on <math>OP</math>
+Link <math>EI</math> and <math>FI</math>, Made line <math>IK\bot EF</math>, then <math>\angle EIK=\angle EOF</math>
+On the other hand, <math>\cos\angle EOF=\frac{EO^2+OF^2-EF^2}{2\cdot EO\cdot OF}=\frac{13}{15}=\cos\angle  EIK</math>
+<math>\sin\angle EOF=\sin\angle EIK=\sqrt{1-\frac{13^2}{15^2}}=\frac{2\sqrt{14}}{15}</math>
+As a result, <math>IE=IO=\frac{45}{\sqrt 14}</math>
+Therefore, <math>OP^2=4\cdot \frac{45^2}{14}=\frac{4050}{7}.</math>
+As a result, <math>m+n=4057\equiv \boxed{057}\pmod{1000}</math>
+==Solution 4==
+Let <math>OP=x</math>.
+Proceed as the first solution in finding that quadrilateral <math>EPFO</math> has side lengths <math>OE=20</math>, <math>OF=24</math>, <math>EP=\sqrt{x^2-20^2}</math>, and <math>PF=\sqrt{x^2-24^2}</math>, and diagonals <math>OP=x</math> and <math>EF=12</math>.
+We note that quadrilateral <math>EPFO</math> is cyclic and use Ptolemy's theorem to solve for <math>x</math>:
+<cmath>20\cdot \sqrt{x^2-24^2} + 12\cdot x = 24\cdot \sqrt{x^2-20^2}</cmath>
+Solving, we have <math>x^2=\frac{4050}{7}</math> so the answer is <math>\boxed{057}</math>.
+-Solution by blueberrieejam
+~bluesoul changes the equation to a right equation, the previous equation isn't solvable
+==Solution 5 (Quick Angle Solution)==
+Let <math>M</math> be the midpoint of <math>AB</math> and <math>N</math> of <math>CD</math>. As <math>\angle OMP = \angle ONP</math>, quadrilateral <math>OMPN</math> is cyclic with diameter <math>OP</math>. By Cyclic quadrilaterals note that <math>\angle MPO = \angle MNO</math>.
+The area of <math>\triangle MNP</math> can be computed by Herons as <cmath>[MNO] = \sqrt{s(s-a)(s-b)(s-c)} = \sqrt{28\cdot 16\cdot 8\cdot 4} = 32\sqrt{14}.</cmath> The area is also <math>\frac{1}{2}ON \cdot MN \sin{\angle MNO}</math>. Therefore,
+<cmath>\begin{align*}
+\sin{\angle MNO} &= \frac{2[MNO]}{ON \cdot MN}  \\
+&= \frac{2}{9}\sqrt{14} \\
+\sin{\angle MNO} &= \frac{OM}{OP} \\
+&= \frac{2}{9}\sqrt{14} \\
+OP &= \frac{90\sqrt{14}}{14} \\
+OP^2 &= \frac{4050}{7} \implies \boxed{057}.
+\end{align*}</cmath>
+~ Aaryabhatta1
+==Solution 6==
+Define <math>M</math> and <math>N</math> as the midpoints of <math>AB</math> and <math>CD</math>, respectively. Because <math>\angle OMP = \angle ONP = 90^{\circ}</math>, we have that <math>ONPM</math> is a cyclic quadrilateral. Hence, <math>\angle PNM = \angle POM.</math> Then, let these two angles be denoted as <math>\alpha</math>.
+Now, assume WLOG that <math>PD = x < 7</math> and <math>PB = y < 15</math> (We can do this because one of <math>PD</math> or <math>PC</math> must be less than 7, and similarly for <math>PB</math> and <math>PA</math>). Then, by Power of a Point on P with respect to the circle with center <math>O</math>, we have that
+<cmath>(14-x)x = (30-y)y</cmath>
+<cmath>(7-x)^{2}+176=(15-y)^{2}.</cmath>
+Then, let <math>z = (7-x)^{2}</math>. From Law of Cosines on <math>\triangle NMP</math>, we have that
+<cmath>\textrm{cos } \angle MNP = \frac{NP^{2}+MN^{2}-MP^{2}}{2 \cdot NP \cdot MN} </cmath>
+<cmath>\textrm{cos } \alpha  = \frac{(7-x)^{2} + 12^{2} - (14-x)^{2}}{24 \cdot (7-x)}.</cmath>
+Plugging in <math>z</math> in gives
+<cmath>\textrm{cos } \alpha  = \frac{-32}{24 \cdot \sqrt{z}}</cmath>
+<cmath>\textrm{cos } \alpha  = \frac{-4}{3\sqrt{z}}</cmath>
+<cmath>\textrm{cos }^{2} \alpha  = \frac{16}{9z}.</cmath>
+Hence,
+<cmath>\textrm{tan }^{2} \alpha  = \frac{\frac{9z-16}{9z}}{\frac{16}{9z}} = \frac{9z-16}{16}.</cmath>
+Then, we also know that
+<cmath>\textrm{tan } \alpha  = \textrm{tan } \angle MOP  = \frac{MP}{OM} = \frac{14-y}{20}.</cmath>
+Squaring this, we get
+<cmath>\textrm{tan }^{2} \alpha  = \frac{z+176}{400}.</cmath>
+Equating our expressions for <math>z</math>, we get
+<math>\frac{z+176}{400} = \frac{9z-16}{16}.</math>
+Solving gives us that
+<math>z = \frac{18}{7}</math>.
+Since <math>\angle ONP = 90^{\circ}</math>, from the Pythagorean Theorem,
+<math>OP^{2} = ON^{2}+PN^{2} = 25^{2}-7^{2} + z = 576+z = \frac{4050}{7}</math>,
+and thus the answer is <math>4050+7 = 4057</math>, which when divided by a thousand leaves a remainder of <math>\boxed{57}.</math>
+-Mr.Sharkman
+Note: my solution was very long and tedious. It was definitely was the least elegant solution. The only thing I like about it is it contains no quadratic equations (unless you count LoC).
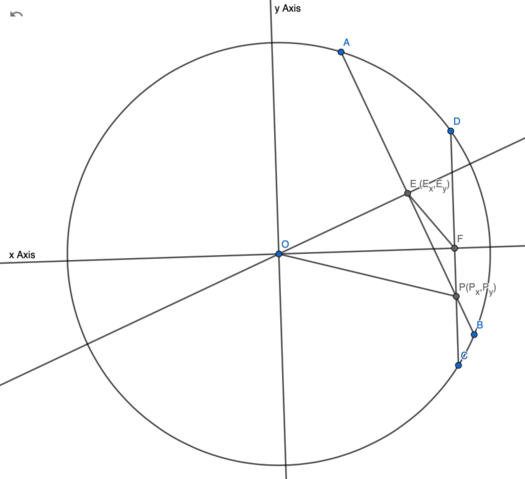
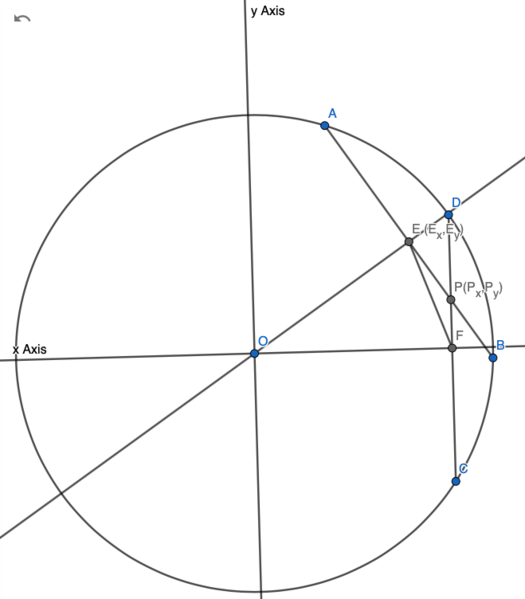
+==Solution 7 Analytic Geometry==
+[[Image:2011 AIMEII Problem 10 CASE 2.png|525px]]
+Let <math>E</math> and <math>F</math> be the midpoints of <math>\overline{AB}</math> and <math>\overline{CD}</math>, respectively, such that <math>\overline{BE}</math> intersects <math>\overline{CF}</math>.
+Since <math>E</math> and <math>F</math> are midpoints, <math>BE = 15</math> and <math>CF = 7</math>.
+<math>B</math> and <math>C</math> are located on the circumference of the circle, so <math>OB = OC = 25</math>.
+Since <math>\overline{OE}\perp \overline{AB}</math> and <math>\overline{OF}\perp \overline{CD}</math>,
+<math>OE = \sqrt{OB^2-BE^2}=20</math> and <math>OF = \sqrt{OC^2-OF^2}=24</math>
+With law of cosines, <math>\cos \angle EOF = \frac{OE^2+OF^2-EF^2}{2\cdot OE\cdot OF} = \frac{13}{15}</math>
+Since <math>EF < OF</math>, <math>\angle EOF</math> is acute angle. <math>\sin \angle EOF = \sqrt{1-\cos^2 \angle EOF} = \frac{\sqrt{56}}{15}</math> and <math>\tan \angle EOF = \frac{\sqrt{56}}{13}</math>
+Let <math>\overline{OF}</math> line be <math>x</math> axis.
+Line <math>\overline{DC}</math> equation is <math>x = OF</math>.
+Since line <math>\overline{AB}</math> passes point <math>E</math> and perpendicular to <math>\overline{OD}</math>, its equation is <math>y - E_y = -\frac{1}{\tan \angle EOF} (x - E_x)</math>
+where <math>E_x = OE\cos{\angle EOF}</math> , <math>E_y = OE\sin{\angle EOF}</math>
+Since <math>P</math> is the intersection of <math>\overline{AB}</math> and <math>\overline{CD}</math>,
+<math>P_x = OF = 24</math>
+<math>P_y = E_y -\frac{1}{\tan \angle EOF} (OF - E_x) = - \frac{3\sqrt{14}}{7}</math> (Negative means point <math>P</math> is between point <math>F</math> and <math>C</math>)
+<math>OP^2 = P_x^2 + P_y^2 = \frac{4050}{7}</math> and the answer is <math>\boxed{057}</math>.
+Note: if <math>EF</math> was longer, point <math>P</math> would be between point <math>D</math> and <math>F</math>. Then, <math>OP</math> would be the diagonal of quadrilateral <math>OEPF</math> not the side. To apply Ptolemy's theorem like solution 4, it is critical to know whether <math>OP</math> is the diagonal or side of quadrilateral. Equation for wrong case cannot be solved. For example,
+[[Image:2011 AIMEII Problem 10 CASE 1.png|525px]]
+==Solution 8 (Analytic- Can use complex numbers or rotation matrix)==
+<cmath>
+We work in the complex plane where \( O = 0 \). Let \( M_1, M_2 \), be midpoints of chords \( AB \), and \( CD \) respectively. \( AB=30 \rightarrow AM=15 \). Since \( AM=15 \), and \( OA=25 \), \( OM_1 = 20 \) by the Pythagorean theorem. WLOG, Let \( M_1 = 20 + 0i \).
+Think about the locus of all points \( M_2 \). By similar logic as above it is any \( M_2 \), such that \( OM_2=24 \). Note that \( M_1M_2 = 12 \). Therefore by LoC on \( \triangle OM_1M_2 \), if \( \angle O = \theta \), \( \cos\theta = \frac{13}{15} \rightarrow \sin\theta = \frac{2\sqrt{14}}{15} \).
+Note that a rotation by \( \theta \) and a scaling of \( \frac{24}{20} = \frac{6}{5} \) transforms \( AB \) to \( DC \).
+This transformation = \( \text{cis}\theta \cdot \frac{6}{5} = \frac{2}{5} \cdot \frac{13 + 2\sqrt{14}i}{5} \).
+Applying the transformation we on \( A,B \) respectively we find: (We are back in Cartesian coordinates now)
+\[
+D = \frac{2}{5} \cdot (52 - 6\sqrt{14}, 39 + 8\sqrt{14}),
+\]
+\[
+C = \frac{2}{5} \cdot (52 + 6\sqrt{14}, -39 + 8\sqrt{14}).
+\]
+To make bashing easier first ignore the \( \frac{2}{5} \).
+e.g. let \( D = 0.4D' \) and \( C = 0.4C' \) and first find the equation of the line passing through \( C' \) and \( D' \).
+After bashing a bit, we get
+\[
+y = \frac{-13}{2\sqrt{14}} \cdot x + \frac{225}{7}\sqrt{14}.
+\]
+Now to account for the \( \frac{2}{5} \) thing we say the actual line is this:
+\[
+y = \frac{-13}{2\sqrt{14}} \cdot x + \frac{2}{5} \cdot \frac{225}{7} \sqrt{14},
+\]
+\[
+y = \frac{-13}{2\sqrt{14}} \cdot x + \frac{90}{7} \sqrt{14}.
+\]
+\( P \) is the intersection of \( CD \) and \( AB \). We have the equation of \( CD \), and \( AB \) is simply \( x = 20 \), so
+Letting \( x = 20 \) we find
+\[
+y = \frac{25\sqrt{14}}{7}.
+\]
+\[
+OP^2 = 20^2 + \left( \frac{25\sqrt{14}}{7} \right)^2 = 5^2 \cdot \left( 4^2 + \left( \frac{5\sqrt{2}}{\sqrt{7}} \right)^2 \right) = 25 \cdot \frac{810}{7} = \frac{4050}{7}.
+\]
+Thus, the answer is \( \boxed{057} \).
+</cmath>
 ==See also==

2011 AIME II (Problems • Answer Key • Resources)
Preceded by Problem 9	Followed by Problem 11
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search