Difference between revisions of "2013 AMC 12B Problems/Problem 24"
Martin13579 (talk | contribs) m |
|||
| (22 intermediate revisions by 13 users not shown) | |||
| Line 1: | Line 1: | ||
==Problem== | ==Problem== | ||
| − | Let <math>ABC</math> be a triangle where <math>M</math> is the midpoint of <math>\overline{AC}</math>, and <math>\overline{CN}</math> is the angle bisector of <math>\angle{ACB}</math> with <math>N</math> on <math>\overline{AB}</math>. Let <math>X</math> be the intersection of the median <math>\overline{BM}</math> and the bisector <math>\overline{CN}</math>. In addition <math>\triangle BXN</math> is equilateral with <math>AC=2</math>. What is <math> | + | Let <math>ABC</math> be a triangle where <math>M</math> is the midpoint of <math>\overline{AC}</math>, and <math>\overline{CN}</math> is the angle bisector of <math>\angle{ACB}</math> with <math>N</math> on <math>\overline{AB}</math>. Let <math>X</math> be the intersection of the median <math>\overline{BM}</math> and the bisector <math>\overline{CN}</math>. In addition <math>\triangle BXN</math> is equilateral with <math>AC=2</math>. What is <math>BX^2</math>? |
<math>\textbf{(A)}\ \frac{10-6\sqrt{2}}{7} \qquad \textbf{(B)}\ \frac{2}{9} \qquad \textbf{(C)}\ \frac{5\sqrt{2}-3\sqrt{3}}{8} \qquad \textbf{(D)}\ \frac{\sqrt{2}}{6} \qquad \textbf{(E)}\ \frac{3\sqrt{3}-4}{5}</math> | <math>\textbf{(A)}\ \frac{10-6\sqrt{2}}{7} \qquad \textbf{(B)}\ \frac{2}{9} \qquad \textbf{(C)}\ \frac{5\sqrt{2}-3\sqrt{3}}{8} \qquad \textbf{(D)}\ \frac{\sqrt{2}}{6} \qquad \textbf{(E)}\ \frac{3\sqrt{3}-4}{5}</math> | ||
| − | ==Solution== | + | ==Solution 1== |
| + | Let <math>BN=x</math> and <math>NA=y</math>. From the conditions, let's deduct some convenient conditions that seem sufficient to solve the problem. | ||
| + | |||
| + | |||
| + | |||
| + | '''<math>M</math> is the midpoint of side <math>AC</math>.''' | ||
| + | |||
| + | This implies that <math>[ABX]=[CBX]</math>. Given that angle <math>ABX</math> is <math>60</math> degrees and angle <math>BXC</math> is <math>120</math> degrees, we can use the area formula to get | ||
| + | |||
| + | <cmath>\frac{1}{2}(x+y)x \frac{\sqrt{3}}{2} = \frac{1}{2} x \cdot CX \frac{\sqrt{3}}{2}</cmath> | ||
| + | |||
| + | So, <math>x+y=CX</math> .....(1) | ||
| + | |||
| + | |||
| + | |||
| + | '''<math>CN</math> is angle bisector.''' | ||
| + | |||
| + | In the triangle <math>ABC</math>, one has <math>BC/AC=x/y</math>, therefore <math>BC=2x/y</math>.....(2) | ||
| + | |||
| + | Furthermore, triangle <math>BCN</math> is similar to triangle <math>MCX</math>, so <math>BC/CM=CN/CX</math>, therefore <math>BC = (CX+x)/CX = (2x+y)/(x+y)</math>....(3) | ||
| + | |||
| + | By (2) and (3) and the subtraction law of ratios, we get | ||
| + | |||
| + | <cmath>BC=2x/y = (2x+y)/(y+x) = y/x</cmath> | ||
| + | |||
| + | Therefore <math>2x^2=y^2</math>, or <math>y=\sqrt{2}x</math>. So <math>BC = 2x/(\sqrt{2}x) = \sqrt{2}</math>. | ||
| + | |||
| + | Finally, using the law of cosine for triangle <math>BCN</math>, we get | ||
| + | |||
| + | <cmath>2 = BC^2 = x^2 + (2x+y)^2 - x(2x+y) = 3x^2 + 3xy + y^2 = \left(5+3\sqrt{2}\right)x^2</cmath> | ||
| + | |||
| + | <cmath>x^2 = \frac{2}{5+3\sqrt{2}} = \boxed{\textbf{(A) }\frac{10-6\sqrt{2}}{7}}.</cmath> | ||
| + | |||
| + | ==Solution 2 (Analytic)== | ||
| + | <center>[[File:2013 AMC 12B 24.jpg]]</center> | ||
| + | |||
| + | |||
| + | Let us dilate triangle <math>ABC</math> so that the sides of equilateral triangle <math>BXN</math> are all equal to <math>2.</math> The purpose of this is to ease the calculations we make in the problem. Given this, we aim to find the length of segment <math>AM</math> so that we can un-dilate triangle <math>ABC</math> by dividing each of its sides by <math>AM</math>. Doing so will make it so that <math>AM = 1</math>, as desired, and doing so will allow us to get the length of <math>BN</math>, whose square is our final answer. | ||
| + | |||
| + | Let <math>O</math> the foot of the altitude from <math>B</math> to <math>NX.</math> On the coordinate plane, position <math>O</math> at <math>(0, 0)</math>, and make <math>NX</math> lie on the x-axis. Since points <math>N</math>, <math>X</math>, and <math>C</math>, are collinear, <math>C</math> must also lie on the x-axis. Additionally, since <math>NX = 2</math>, <math>OB = \sqrt{3}</math>, meaning that we can position point <math>B</math> at <math>(0, \sqrt{3})</math>. Now, notice that line <math>\overline{AB}</math> has the equation <math>y = \sqrt{3}x + \sqrt{3}</math> and that line <math>\overline{BM}</math> has the equation <math>y = -\sqrt{3}x + \sqrt{3}</math> because angles <math>BNX</math> and <math>BXN</math> are both <math>60^{\circ}</math>. We can then position <math>A</math> at point <math>(n, \sqrt{3}(n + 1))</math> and <math>C</math> at point <math>(p, 0)</math>. Quickly note that, because <math>CN</math> is an angle bisector, <math>AC</math> must pass through the point <math>(0, -\sqrt{3})</math>. | ||
| + | |||
| + | We proceed to construct a system of equations. First observe that the midpoint <math>M</math> of <math>AC</math> must lie on <math>BM</math>, with the equation <math>y = -\sqrt{3}x + \sqrt{3}</math>. The coordinates of <math>M</math> are <math>\left(\frac{p + n}{2}, \frac{\sqrt{3}}{2}(n + 1)\right)</math>, and we can plug in these coordinates into the equation of line <math>BM</math>, yielding that <cmath>\frac{\sqrt{3}}{2}(n + 1) = -\sqrt{3}(\frac{p + n}{2}) + \sqrt{3} \implies n + 1 = -p - n + 2 \implies p = -2n + 1.</cmath> For our second equation, notice that line <math>AC</math> has equation <math>y = \frac{\sqrt{3}}{p}x - \sqrt{3}</math>. Midpoint <math>M</math> must also lie on this line, and we can substitute coordinates again to get <cmath>\frac{\sqrt{3}}{2}(n + 1) = \frac{\sqrt{3}}{p}(\frac{p + n}{2}) - \sqrt{3} \implies n + 1 = \frac{p + n}{p} - 2 \implies n + 1 = \frac{n}{p} - 1</cmath> <cmath>\implies p = \frac{n}{n + 2}.</cmath> | ||
| + | |||
| + | Setting both equations equal to each other and multiplying both sides by <math>(n + 2)</math>, we have that <math>-2n^2 - 4n + n + 2 = n \implies -2n^2 - 4n + 2 = 0</math>, which in turn simplifies into <math>0 = n^2 + 2n - 1</math> when dividing the entire equation by <math>-2.</math> Using the quadratic formula, we have that <cmath>n = \frac{-2 \pm \sqrt{4 + 4}}{2} = -1 - \sqrt{2}.</cmath> Here, we discard the positive root since <math>A</math> must lie to the left of the y-axis. Then, the coordinates of <math>C</math> are <math>(3 + 2\sqrt{2}, 0)</math>, and the coordinates of <math>A</math> are <math>(-1 - \sqrt{2}, -\sqrt{6}).</math> Seeing that segment <math>AM</math> has half the length of side <math>AC</math>, we have that the length of <math>AM</math> is <cmath>\frac{\sqrt{(3 + 2\sqrt{2} - (-1 - \sqrt{2}))^2 + (\sqrt{6})^2}}{2} = \frac{\sqrt{16 + 24\sqrt{2} + 18 + 6}}{2} = \sqrt{10 + 6\sqrt{2}}.</cmath> | ||
| + | |||
| + | Now, we divide each side length of <math>\triangle ABC</math> by <math>AM</math>, and from this, <math>BN^2</math> will equal <math>\left(\frac{2}{\sqrt{10 + 6\sqrt{2}}}\right)^2 = \frac{2}{5+3\sqrt{2}} = \boxed{\textbf{(A) }\frac{10-6\sqrt{2}}{7}.}</math> | ||
| + | |||
| + | ==Solution 3 == | ||
| + | |||
| + | By some angle-chasing, we find that <math>\triangle ANC \sim \triangle BXC</math>. From here, construct a point <math>D</math> on <math>AC</math> such that <math>\triangle DXC \sim \triangle ANC</math>. Now, let <math>BC = a</math>, which means that <math>DM = a - 1</math> and <math>AD = 2 - a</math>, and let <math>BN = BX = XN = XD = DN = b</math>. Note that we want to compute <math>b^2</math>. Because <math>\triangle AND \sim \triangle DXM</math>, we have: | ||
| + | |||
| + | <cmath>\frac{AN}{2-a} = \frac{b}{a-1} \implies AN = \frac{b(2-a)}{(a-1)}</cmath> | ||
| + | |||
| + | However, we have more similar triangles. In fact, going back to our original pair of similar triangles - <math>\triangle ANC</math> and <math>\triangle BXC</math> - gives us more similarity ratios: | ||
| + | |||
| + | <cmath>\frac{AN}{AC} = \frac{BX}{BC} \implies \frac{\frac{b(2-a)}{(a-1)}}{2} = \frac{b}{a} \implies a = \sqrt{2}</cmath> | ||
| + | |||
| + | Since we constructed point <math>D</math> such that <math>DX</math> is parallel to <math>AB</math>, we now examine trapezoid <math>ABXD</math>. From the variables that we already set up, we know that <math>AB = b + b\sqrt{2}, BX = XD = b</math>, and <math>DA = 2 - \sqrt{2}</math>. Let <math>X'</math> denote the foot of the perpendicular from <math>X</math> to base <math>AB</math> and define <math>D'</math> similarly. | ||
| + | |||
| + | Because <math>\triangle BXX'</math> is a <math>30, 60, 90</math> triangle, <math>XX' = \frac{b\sqrt{3}}{2}</math> and <math>BX' = \frac{b}{2}</math>. Thus, <math>D'A = b\sqrt{2} - \frac{b}{2}</math> and <math>DD' = XX' = \frac{b\sqrt{3}}{2}</math>. By the Pythagorean Theorem on <math>\triangle ADD'</math>, | ||
| + | |||
| + | <cmath>\left (b\sqrt{2} - \frac{b}{2} \right)^2 + \left(\frac{b\sqrt{3}}{2} \right)^2 = \left(2 - \sqrt{2} \right)^2 \implies b^2 = \boxed{\textbf{(A) } \frac{10-6\sqrt{2}}{7}}</cmath>. | ||
| + | |||
| + | |||
| + | ==Solution 4 == | ||
| + | Since <math>\triangle BXN</math> is equilateral, let's assume the sides of them are all <math>a</math>, and denote the length of <math>XM</math> is <math>m</math>. Since <math>CN</math> bisects <math>\angle BCA</math>, applying the angle bisector theorem and we can get <math>BC=\frac{a}{m}</math>;<math>AN=2m</math>. Now applying LOC, we can get <math>(a+2m)^2+(a+m)^2-2(a+2m)(a+m)\cos\frac{\pi}{3}=1</math>. We get <math>a^2+3m^2+3am=1</math>. Now applying the Stewart theorem in <math>\triangle BAC</math>, we can find that <math>{\frac{a^2}{m^2}+(a+2m)^2=2(1+(a+m)^2)}</math>, after simplifying, we get <math>{\frac{a^2}{m^2}-a^2+2m^2=2}</math>. After observation, the main key for this problem is <math>a^2</math>, so we can solve <math>a</math> in term of <math>m</math>. Let's see the equation <math>{\frac{a^2}{m^2}-a^2+2m^2=2}</math>, we can find that <math>a=\sqrt{2}m</math> so <math>a^2=2m^2</math>. Now back solving the first equation we can get that <math>a=\frac{-3m+\sqrt{4-3m^2}}{m}</math>cuz the negative one can't work. After solving, we can get that <math>m^2=\frac{1}{5+3\sqrt{2}}</math> so <math>a^2=2m^2</math> and we get <math>a^2 = \boxed{\textbf{(A) } \frac{10-6\sqrt{2}}{7}}</math>~ bluesoul | ||
| + | |||
| + | ==Solution 5 (Similar Triangles)== | ||
| + | |||
| + | Denote the length of <math>AN</math> as <math>a</math> and the length of <math>NB</math> as <math>b.</math> | ||
| + | |||
| + | Let <math>M'</math> be the midpoint of <math>\overline{BC} .</math> Denote the intersection of <math>\overline{MM'}</math> and <math>\overline{CN}</math> as <math>X' .</math> Note that <math>MX' = \frac12 AN = \frac{a}{2}</math> and <math>CN = 2\cdot NX' .</math> As <math>\overline{MM'} || \overline{AB},</math> we have that <math>\triangle MXX' \sim \triangle BXN</math> or <math>\triangle MXX'</math> is equilateral and <math>XX' =MX' = \frac{a}{2}.</math> Thus, <math>CN = 2b+a</math> and <math>CX=a+b.</math> | ||
| + | |||
| + | Observe that | ||
| + | |||
| + | <cmath>\triangle BXC\sim \triangle ANC \implies \frac{BX}{XC} =\frac{AN}{NC} \implies \frac{b}{b+a} = \frac{a}{2b+a} \implies a = \sqrt 2 b.</cmath> | ||
| + | |||
| + | By the angle bisector theorem, we have that <math>BC=\frac{2b}{a} = \sqrt 2.</math> | ||
| + | |||
| + | We apply the Law of Cosines on <math>\triangle BXC</math> as follows: | ||
| + | <cmath> | ||
| + | BC^2=BX^2+XC^2-2BX\cdot XC\cdot \cos120^\circ | ||
| + | </cmath> | ||
| + | <cmath>\begin{align*} | ||
| + | 2&=b^2+(\sqrt 2+1)^2b^2 +(\sqrt2 + 1)b^2 \\ | ||
| + | &=b^2(5+3\sqrt 2) | ||
| + | \end{align*}</cmath> | ||
| + | or | ||
| + | <cmath>\boxed{b^2=\textbf{(A) } \frac{10-6\sqrt{2}}{7}}</cmath> | ||
| + | |||
| + | ~ASAB | ||
| + | |||
| + | ==Solution 6== | ||
| + | |||
| + | [[File:2013AMC12BProblem24Solution6.png|center|500px]] | ||
| + | |||
| + | <math>\angle BXC = \angle ANC</math>, <math>\angle BCX = \angle ACN</math>, <math>\triangle BCX \sim \triangle ACN</math>, <math>\frac{CX}{CN} = \frac{BC}{AC}</math> | ||
| + | |||
| + | <math>\angle MBC = \angle BAC</math>, <math>\angle BCM = \angle ACB</math>, <math>\triangle BCM \sim \triangle ACB</math>, <math>\frac{BC}{AC} = \frac{CM}{BC}</math>, <math>BC = \sqrt{2}</math> | ||
| + | |||
| + | Let <math>BX = x</math>, <math>CN = CX + x</math>, <math>\frac{CX}{CX + x} = \frac{\sqrt{2}}{2}</math>, <math>2CX = CX \sqrt{2} + x \sqrt{2}</math>, <math>CX = x(\sqrt{2} + 1)</math> | ||
| + | |||
| + | <math>BC^2 = BX^2 + CX^2 - 2 \cdot BX \cdot CX \cdot \cos 120^\circ</math> | ||
| + | |||
| + | <math>2 = x^2(\sqrt{2} + 1)^2 + x^2 + x^2(\sqrt{2} + 1) = 5x^2 + 3x^2 \sqrt{2}</math> | ||
| + | |||
| + | <math>x^2 = \frac{2}{5 + 3 \sqrt{2} } = \boxed{\textbf{(A) }\frac{10-6\sqrt{2}}{7}}</math> | ||
| + | |||
| + | ~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen] | ||
| + | |||
| + | ==Video Solution by MOP 2024== | ||
| + | https://youtu.be/y0s6OTQ7KfI | ||
| + | |||
| + | ~r00tsOfUnity | ||
== See also == | == See also == | ||
{{AMC12 box|year=2013|ab=B|num-b=23|num-a=25}} | {{AMC12 box|year=2013|ab=B|num-b=23|num-a=25}} | ||
| + | |||
| + | [[Category:Introductory Geometry Problems]] | ||
| + | {{MAA Notice}} | ||
Latest revision as of 21:49, 20 October 2024
Contents
Problem
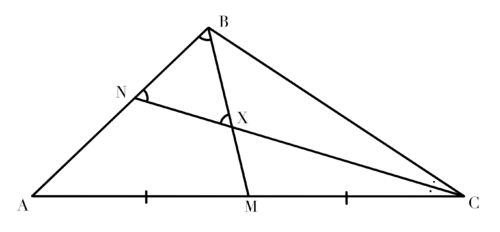
Let ![]() be a triangle where
be a triangle where ![]() is the midpoint of
is the midpoint of ![]() , and
, and ![]() is the angle bisector of
is the angle bisector of ![]() with
with ![]() on
on ![]() . Let
. Let ![]() be the intersection of the median
be the intersection of the median ![]() and the bisector
and the bisector ![]() . In addition
. In addition ![]() is equilateral with
is equilateral with ![]() . What is
. What is ![]() ?
?
![]()
Solution 1
Let ![]() and
and ![]() . From the conditions, let's deduct some convenient conditions that seem sufficient to solve the problem.
. From the conditions, let's deduct some convenient conditions that seem sufficient to solve the problem.
![]() is the midpoint of side
is the midpoint of side ![]() .
.
This implies that ![]() . Given that angle
. Given that angle ![]() is
is ![]() degrees and angle
degrees and angle ![]() is
is ![]() degrees, we can use the area formula to get
degrees, we can use the area formula to get
![]()
So, ![]() .....(1)
.....(1)
![]() is angle bisector.
is angle bisector.
In the triangle ![]() , one has
, one has ![]() , therefore
, therefore ![]() .....(2)
.....(2)
Furthermore, triangle ![]() is similar to triangle
is similar to triangle ![]() , so
, so ![]() , therefore
, therefore ![]() ....(3)
....(3)
By (2) and (3) and the subtraction law of ratios, we get
![]()
Therefore ![]() , or
, or ![]() . So
. So ![]() .
.
Finally, using the law of cosine for triangle ![]() , we get
, we get
![]()
![\[x^2 = \frac{2}{5+3\sqrt{2}} = \boxed{\textbf{(A) }\frac{10-6\sqrt{2}}{7}}.\]](http://latex.artofproblemsolving.com/c/5/b/c5bbf4b26fd67dfacb45e0e5197c4c6d43764447.png)
Solution 2 (Analytic)

Let us dilate triangle ![]() so that the sides of equilateral triangle
so that the sides of equilateral triangle ![]() are all equal to
are all equal to ![]() The purpose of this is to ease the calculations we make in the problem. Given this, we aim to find the length of segment
The purpose of this is to ease the calculations we make in the problem. Given this, we aim to find the length of segment ![]() so that we can un-dilate triangle
so that we can un-dilate triangle ![]() by dividing each of its sides by
by dividing each of its sides by ![]() . Doing so will make it so that
. Doing so will make it so that ![]() , as desired, and doing so will allow us to get the length of
, as desired, and doing so will allow us to get the length of ![]() , whose square is our final answer.
, whose square is our final answer.
Let ![]() the foot of the altitude from
the foot of the altitude from ![]() to
to ![]() On the coordinate plane, position
On the coordinate plane, position ![]() at
at ![]() , and make
, and make ![]() lie on the x-axis. Since points
lie on the x-axis. Since points ![]() ,
, ![]() , and
, and ![]() , are collinear,
, are collinear, ![]() must also lie on the x-axis. Additionally, since
must also lie on the x-axis. Additionally, since ![]() ,
, ![]() , meaning that we can position point
, meaning that we can position point ![]() at
at ![]() . Now, notice that line
. Now, notice that line ![]() has the equation
has the equation ![]() and that line
and that line ![]() has the equation
has the equation ![]() because angles
because angles ![]() and
and ![]() are both
are both ![]() . We can then position
. We can then position ![]() at point
at point ![]() and
and ![]() at point
at point ![]() . Quickly note that, because
. Quickly note that, because ![]() is an angle bisector,
is an angle bisector, ![]() must pass through the point
must pass through the point ![]() .
.
We proceed to construct a system of equations. First observe that the midpoint ![]() of
of ![]() must lie on
must lie on ![]() , with the equation
, with the equation ![]() . The coordinates of
. The coordinates of ![]() are
are  , and we can plug in these coordinates into the equation of line
, and we can plug in these coordinates into the equation of line ![]() , yielding that
, yielding that ![]() For our second equation, notice that line
For our second equation, notice that line ![]() has equation
has equation ![]() . Midpoint
. Midpoint ![]() must also lie on this line, and we can substitute coordinates again to get
must also lie on this line, and we can substitute coordinates again to get ![]()
![]()
Setting both equations equal to each other and multiplying both sides by ![]() , we have that
, we have that ![]() , which in turn simplifies into
, which in turn simplifies into ![]() when dividing the entire equation by
when dividing the entire equation by ![]() Using the quadratic formula, we have that
Using the quadratic formula, we have that ![]() Here, we discard the positive root since
Here, we discard the positive root since ![]() must lie to the left of the y-axis. Then, the coordinates of
must lie to the left of the y-axis. Then, the coordinates of ![]() are
are ![]() , and the coordinates of
, and the coordinates of ![]() are
are ![]() Seeing that segment
Seeing that segment ![]() has half the length of side
has half the length of side ![]() , we have that the length of
, we have that the length of ![]() is
is ![\[\frac{\sqrt{(3 + 2\sqrt{2} - (-1 - \sqrt{2}))^2 + (\sqrt{6})^2}}{2} = \frac{\sqrt{16 + 24\sqrt{2} + 18 + 6}}{2} = \sqrt{10 + 6\sqrt{2}}.\]](http://latex.artofproblemsolving.com/7/3/7/737b6112642355380d38776159bce2f2665a857b.png)
Now, we divide each side length of ![]() by
by ![]() , and from this,
, and from this, ![]() will equal
will equal 
Solution 3
By some angle-chasing, we find that ![]() . From here, construct a point
. From here, construct a point ![]() on
on ![]() such that
such that ![]() . Now, let
. Now, let ![]() , which means that
, which means that ![]() and
and ![]() , and let
, and let ![]() . Note that we want to compute
. Note that we want to compute ![]() . Because
. Because ![]() , we have:
, we have:
![]()
However, we have more similar triangles. In fact, going back to our original pair of similar triangles - ![]() and
and ![]() - gives us more similarity ratios:
- gives us more similarity ratios:
![]()
Since we constructed point ![]() such that
such that ![]() is parallel to
is parallel to ![]() , we now examine trapezoid
, we now examine trapezoid ![]() . From the variables that we already set up, we know that
. From the variables that we already set up, we know that ![]() , and
, and ![]() . Let
. Let ![]() denote the foot of the perpendicular from
denote the foot of the perpendicular from ![]() to base
to base ![]() and define
and define ![]() similarly.
similarly.
Because ![]() is a
is a ![]() triangle,
triangle, ![]() and
and ![]() . Thus,
. Thus, ![]() and
and ![]() . By the Pythagorean Theorem on
. By the Pythagorean Theorem on ![]() ,
,
![\[\left (b\sqrt{2} - \frac{b}{2} \right)^2 + \left(\frac{b\sqrt{3}}{2} \right)^2 = \left(2 - \sqrt{2} \right)^2 \implies b^2 = \boxed{\textbf{(A) } \frac{10-6\sqrt{2}}{7}}\]](http://latex.artofproblemsolving.com/8/9/f/89f4e203f663e7b67b160a223a77faff67893141.png) .
.
Solution 4
Since ![]() is equilateral, let's assume the sides of them are all
is equilateral, let's assume the sides of them are all ![]() , and denote the length of
, and denote the length of ![]() is
is ![]() . Since
. Since ![]() bisects
bisects ![]() , applying the angle bisector theorem and we can get
, applying the angle bisector theorem and we can get ![]() ;
;![]() . Now applying LOC, we can get
. Now applying LOC, we can get ![]() . We get
. We get ![]() . Now applying the Stewart theorem in
. Now applying the Stewart theorem in ![]() , we can find that
, we can find that ![]() , after simplifying, we get
, after simplifying, we get ![]() . After observation, the main key for this problem is
. After observation, the main key for this problem is ![]() , so we can solve
, so we can solve ![]() in term of
in term of ![]() . Let's see the equation
. Let's see the equation ![]() , we can find that
, we can find that ![]() so
so ![]() . Now back solving the first equation we can get that
. Now back solving the first equation we can get that ![]() cuz the negative one can't work. After solving, we can get that
cuz the negative one can't work. After solving, we can get that ![]() so
so ![]() and we get
and we get  ~ bluesoul
~ bluesoul
Solution 5 (Similar Triangles)
Denote the length of ![]() as
as ![]() and the length of
and the length of ![]() as
as ![]()
Let ![]() be the midpoint of
be the midpoint of ![]() Denote the intersection of
Denote the intersection of ![]() and
and ![]() as
as ![]() Note that
Note that ![]() and
and ![]() As
As ![]() we have that
we have that ![]() or
or ![]() is equilateral and
is equilateral and ![]() Thus,
Thus, ![]() and
and ![]()
Observe that
![]()
By the angle bisector theorem, we have that ![]()
We apply the Law of Cosines on ![]() as follows:
as follows:
![]()
 or
or
![\[\boxed{b^2=\textbf{(A) } \frac{10-6\sqrt{2}}{7}}\]](http://latex.artofproblemsolving.com/d/2/8/d284966b2295dfa152a43c43c34d71fc28ddf373.png)
~ASAB
Solution 6
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
Let ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]()
![]()

Video Solution by MOP 2024
~r00tsOfUnity
See also
| 2013 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 23 |
Followed by Problem 25 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.