Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2001 AMC 10 Problems/Problem 5"

(→‎Solution)
 
(5 intermediate revisions by 5 users not shown)
Line 1: Line 1:
 
== Problem ==
 
== Problem ==
  
−
How many of the twelve pentominoes pictured below at least one line of symmetry?
+
How many of the twelve pentominoes pictured below have at least one line of reflectional symmetry?
  
−
<math> \textbf{(A)}\ 3 \qquad \textbf{(B)}\ 4 \qquad \textbf{(C)}\ 5 \qquad \textbf{(D)}\ 6 \qquad \textbf{(E)}\ 7 </math>
+
<asy>
 +
unitsize(5mm);
 +
defaultpen(linewidth(1pt));
 +
draw(shift(2,0)*unitsquare);
 +
draw(shift(2,1)*unitsquare);
 +
draw(shift(2,2)*unitsquare);
 +
draw(shift(1,2)*unitsquare);
 +
draw(shift(0,2)*unitsquare);
 +
draw(shift(2,4)*unitsquare);
 +
draw(shift(2,5)*unitsquare);
 +
draw(shift(2,6)*unitsquare);
 +
draw(shift(1,5)*unitsquare);
 +
draw(shift(0,5)*unitsquare);
 +
draw(shift(4,8)*unitsquare);
 +
draw(shift(3,8)*unitsquare);
 +
draw(shift(2,8)*unitsquare);
 +
draw(shift(1,8)*unitsquare);
 +
draw(shift(0,8)*unitsquare);
 +
draw(shift(6,8)*unitsquare);
 +
draw(shift(7,8)*unitsquare);
 +
draw(shift(8,8)*unitsquare);
 +
draw(shift(9,8)*unitsquare);
 +
draw(shift(9,9)*unitsquare);
 +
draw(shift(6,5)*unitsquare);
 +
draw(shift(7,5)*unitsquare);
 +
draw(shift(8,5)*unitsquare);
 +
draw(shift(7,6)*unitsquare);
 +
draw(shift(7,4)*unitsquare);
 +
draw(shift(6,1)*unitsquare);
 +
draw(shift(7,1)*unitsquare);
 +
draw(shift(8,1)*unitsquare);
 +
draw(shift(6,0)*unitsquare);
 +
draw(shift(7,2)*unitsquare);
 +
draw(shift(11,8)*unitsquare);
 +
draw(shift(12,8)*unitsquare);
 +
draw(shift(13,8)*unitsquare);
 +
draw(shift(14,8)*unitsquare);
 +
draw(shift(13,9)*unitsquare);
 +
draw(shift(11,5)*unitsquare);
 +
draw(shift(12,5)*unitsquare);
 +
draw(shift(13,5)*unitsquare);
 +
draw(shift(11,6)*unitsquare);
 +
draw(shift(13,4)*unitsquare);
 +
draw(shift(11,1)*unitsquare);
 +
draw(shift(12,1)*unitsquare);
 +
draw(shift(13,1)*unitsquare);
 +
draw(shift(13,2)*unitsquare);
 +
draw(shift(14,2)*unitsquare);
 +
draw(shift(16,8)*unitsquare);
 +
draw(shift(17,8)*unitsquare);
 +
draw(shift(18,8)*unitsquare);
 +
draw(shift(17,9)*unitsquare);
 +
draw(shift(18,9)*unitsquare);
 +
draw(shift(16,5)*unitsquare);
 +
draw(shift(17,6)*unitsquare);
 +
draw(shift(18,5)*unitsquare);
 +
draw(shift(16,6)*unitsquare);
 +
draw(shift(18,6)*unitsquare);
 +
draw(shift(16,0)*unitsquare);
 +
draw(shift(17,0)*unitsquare);
 +
draw(shift(17,1)*unitsquare);
 +
draw(shift(18,1)*unitsquare);
 +
draw(shift(18,2)*unitsquare);</asy>
 +
 
 +
<math>\textbf{(A) } 3 \qquad\textbf{(B) } 4 \qquad\textbf{(C) } 5 \qquad\textbf{(D) } 6 \qquad\textbf{(E) } 7</math>
  
 
== Solution ==
 
== Solution ==
Line 11: Line 75:
 
The ones with lines over the shapes have at least one line of symmetry. Counting the number of shapes that have line(s) on them,
 
The ones with lines over the shapes have at least one line of symmetry. Counting the number of shapes that have line(s) on them,
 
we find <math> \boxed{\textbf{(D)}\ 6} </math> pentominoes.
 
we find <math> \boxed{\textbf{(D)}\ 6} </math> pentominoes.
 +
 +
==Video Solution by Daily Dose of Math==
 +
 +
https://youtu.be/svFpNvUUY7E?si=CloMWtqbbhBNgWy_
 +
 +
~Thesmartgreekmathdude
  
 
== See Also ==
 
== See Also ==
  
 
{{AMC10 box|year=2001|num-b=4|num-a=6}}
 
{{AMC10 box|year=2001|num-b=4|num-a=6}}
 +
{{MAA Notice}}

Latest revision as of 15:11, 15 July 2024

Problem

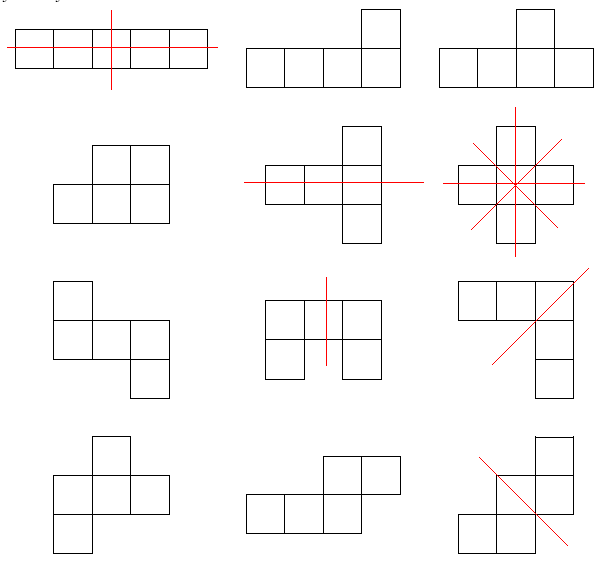
How many of the twelve pentominoes pictured below have at least one line of reflectional symmetry?

[asy] unitsize(5mm); defaultpen(linewidth(1pt)); draw(shift(2,0)*unitsquare); draw(shift(2,1)*unitsquare); draw(shift(2,2)*unitsquare); draw(shift(1,2)*unitsquare); draw(shift(0,2)*unitsquare); draw(shift(2,4)*unitsquare); draw(shift(2,5)*unitsquare); draw(shift(2,6)*unitsquare); draw(shift(1,5)*unitsquare); draw(shift(0,5)*unitsquare); draw(shift(4,8)*unitsquare); draw(shift(3,8)*unitsquare); draw(shift(2,8)*unitsquare); draw(shift(1,8)*unitsquare); draw(shift(0,8)*unitsquare); draw(shift(6,8)*unitsquare); draw(shift(7,8)*unitsquare); draw(shift(8,8)*unitsquare); draw(shift(9,8)*unitsquare); draw(shift(9,9)*unitsquare); draw(shift(6,5)*unitsquare); draw(shift(7,5)*unitsquare); draw(shift(8,5)*unitsquare); draw(shift(7,6)*unitsquare); draw(shift(7,4)*unitsquare); draw(shift(6,1)*unitsquare); draw(shift(7,1)*unitsquare); draw(shift(8,1)*unitsquare); draw(shift(6,0)*unitsquare); draw(shift(7,2)*unitsquare); draw(shift(11,8)*unitsquare); draw(shift(12,8)*unitsquare); draw(shift(13,8)*unitsquare); draw(shift(14,8)*unitsquare); draw(shift(13,9)*unitsquare); draw(shift(11,5)*unitsquare); draw(shift(12,5)*unitsquare); draw(shift(13,5)*unitsquare); draw(shift(11,6)*unitsquare); draw(shift(13,4)*unitsquare); draw(shift(11,1)*unitsquare); draw(shift(12,1)*unitsquare); draw(shift(13,1)*unitsquare); draw(shift(13,2)*unitsquare); draw(shift(14,2)*unitsquare); draw(shift(16,8)*unitsquare); draw(shift(17,8)*unitsquare); draw(shift(18,8)*unitsquare); draw(shift(17,9)*unitsquare); draw(shift(18,9)*unitsquare); draw(shift(16,5)*unitsquare); draw(shift(17,6)*unitsquare); draw(shift(18,5)*unitsquare); draw(shift(16,6)*unitsquare); draw(shift(18,6)*unitsquare); draw(shift(16,0)*unitsquare); draw(shift(17,0)*unitsquare); draw(shift(17,1)*unitsquare); draw(shift(18,1)*unitsquare); draw(shift(18,2)*unitsquare);[/asy]

$\textbf{(A) } 3 \qquad\textbf{(B) } 4 \qquad\textbf{(C) } 5 \qquad\textbf{(D) } 6 \qquad\textbf{(E) } 7$

Solution

Pentonimoes.gif

The ones with lines over the shapes have at least one line of symmetry. Counting the number of shapes that have line(s) on them, we find $\boxed{\textbf{(D)}\ 6}$ pentominoes.

Video Solution by Daily Dose of Math

https://youtu.be/svFpNvUUY7E?si=CloMWtqbbhBNgWy_

~Thesmartgreekmathdude

See Also

2001 AMC 10 (Problems • Answer Key • Resources)
Preceded by
Problem 4 		Followed by
Problem 6
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2001_AMC_10_Problems/Problem_5&oldid=222625"