Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2012 AMC 12B Problems/Problem 19"

(Created page with "==Solution== File:2012_AMC-12B-19‎.jpg Observe the diagram above. Each dot represents one of the six vertices of the regular octahedron. Three dots have been placed exact...")
 
(→‎Solution 1)
 
(18 intermediate revisions by 12 users not shown)
Line 1: Line 1:
−
==Solution==
+
==Problem==
 +
A unit cube has vertices <math>P_1,P_2,P_3,P_4,P_1',P_2',P_3',</math> and <math>P_4'</math>. Vertices <math>P_2</math>, <math>P_3</math>, and <math>P_4</math> are adjacent to <math>P_1</math>, and for <math>1\le i\le 4,</math> vertices <math>P_i</math> and <math>P_i'</math> are opposite to each other. A regular octahedron has one vertex in each of the segments <math>P_1P_2</math>, <math>P_1P_3</math>, <math>P_1P_4</math>, <math>P_1'P_2'</math>, <math>P_1'P_3'</math>, and <math>P_1'P_4'</math>. What is the octahedron's side length?
 +
 
 +
<asy>
 +
import three;
 +
 
 +
size(7.5cm);
 +
triple eye = (-4, -8, 3);
 +
currentprojection = perspective(eye);
 +
 
 +
triple[] P = {(1, -1, -1), (-1, -1, -1), (-1, 1, -1), (-1, -1, 1), (1, -1, -1)}; // P[0] = P[4] for convenience
 +
triple[] Pp = {-P[0], -P[1], -P[2], -P[3], -P[4]};
 +
 
 +
// draw octahedron
 +
triple pt(int k){ return (3*P[k] + P[1])/4; }
 +
triple ptp(int k){ return (3*Pp[k] + Pp[1])/4; }
 +
draw(pt(2)--pt(3)--pt(4)--cycle, gray(0.6));
 +
draw(ptp(2)--pt(3)--ptp(4)--cycle, gray(0.6));
 +
draw(ptp(2)--pt(4), gray(0.6));
 +
draw(pt(2)--ptp(4), gray(0.6));
 +
draw(pt(4)--ptp(3)--pt(2), gray(0.6) + linetype("4 4"));
 +
draw(ptp(4)--ptp(3)--ptp(2), gray(0.6) + linetype("4 4"));
 +
 
 +
// draw cube
 +
for(int i = 0; i < 4; ++i){
 +
draw(P[1]--P[i]); draw(Pp[1]--Pp[i]);
 +
for(int j = 0; j < 4; ++j){
 +
if(i == 1 || j == 1 || i == j) continue;
 +
draw(P[i]--Pp[j]); draw(Pp[i]--P[j]);
 +
}
 +
dot(P[i]); dot(Pp[i]);
 +
dot(pt(i)); dot(ptp(i));
 +
}
 +
 
 +
label("$P_1$", P[1], dir(P[1]));
 +
label("$P_2$", P[2], dir(P[2]));
 +
label("$P_3$", P[3], dir(-45));
 +
label("$P_4$", P[4], dir(P[4]));
 +
label("$P'_1$", Pp[1], dir(Pp[1]));
 +
label("$P'_2$", Pp[2], dir(Pp[2]));
 +
label("$P'_3$", Pp[3], dir(-100));
 +
label("$P'_4$", Pp[4], dir(Pp[4]));
 +
</asy>
 +
 
 +
<math>\textbf{(A)}\ \frac{3\sqrt{2}}{4}\qquad\textbf{(B)}\ \frac{7\sqrt{6}}{16}\qquad\textbf{(C)}\ \frac{\sqrt{5}}{2}\qquad\textbf{(D)}\ \frac{2\sqrt{3}}{3}\qquad\textbf{(E)}\ \frac{\sqrt{6}}{2}</math>
 +
 
 +
==Solution 1==
  
 
[[File:2012_AMC-12B-19‎.jpg]]
 
[[File:2012_AMC-12B-19‎.jpg]]
  
−
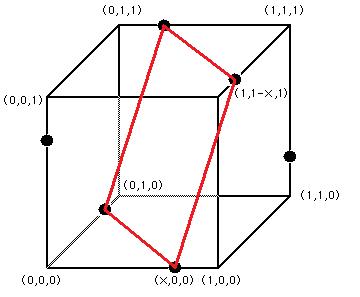
Observe the diagram above. Each dot represents one of the six vertices of the regular octahedron. Three dots have been placed exactly x units from the (0,0,0) corner of the unit cube. The other three dots have been placed exactly x units from the (1,1,1) corner of the unit cube. A red square has been drawn connecting four of the dots to provide perspective regarding the shape of the octahedron. Observe that the three dots that are near (0,0,0) are each x*sqrt(2) from each other. The same is true for the three dots that are near (1,1,1). There is a unique x for which the rectangle drawn in red becomes a square. This will occur when the distance from (x,0,0) to (1,1-x, 1) is x*sqrt(2).
+
Observe the diagram above. Each dot represents one of the six vertices of the regular octahedron. Three dots have been placed exactly x units from the <math>(0,0,0)</math> corner of the unit cube. The other three dots have been placed exactly x units from the <math>(1,1,1)</math> corner of the unit cube. A red square has been drawn connecting four of the dots to provide perspective regarding the shape of the octahedron. Observe that the three dots that are near <math>(0,0,0)</math> are each <math>(x)(\sqrt{2}</math>) from each other. The same is true for the three dots that are near <math>(1,1,1).</math> There is a unique <math>x</math> for which the rectangle drawn in red becomes a square. This will occur when the distance from <math>(x,0,0)</math> to <math>(1,1-x, 1)</math> is <math>(x)(\sqrt{2}</math>).
  
  
−
Using the distance formula we find the distance between the two points to be: sqrt((1-x)^2 + (1-x)^2 + 1) = sqrt(2x^2 - 4x +3). Equating this to x*sqrt(2) and squaring both sides, we have the equation:
+
Using the distance formula we find the distance between the two points to be: <math>\sqrt{{(1-x)^2} + {(1-x)^2} + 1}</math> = <math>\sqrt{2x^2 - 4x +3}</math>. Equating this to <math>(x)(\sqrt{2}</math>) and squaring both sides, we have the equation:
  
−
2x^2 - 4x + 3 = 2x^2
+
<math>2{x^2} - 4x + 3</math> = <math>2{x^2}</math>
  
−
-4x + 3 = 0
+
<math>-4x + 3 = 0</math>
  
−
x = 3/4.
+
<math>x</math> = <math>\frac{3} {4}</math>.
  
  
−
Since the length of each side is x*sqrt(2), we have a final result of 3sqrt(2)/4. Thus, Answer choice A is correct.
+
Since the length of each side is <math>(x)(\sqrt{2}</math>), we have a final result of <math>\frac{3 \sqrt{2}}{4}</math>. Thus, Answer choice <math>\boxed{\text{A}}</math> is correct.
  
  
Line 21: Line 67:
  
 
--[[User:Jm314|Jm314]] 14:55, 26 February 2012 (EST)
 
--[[User:Jm314|Jm314]] 14:55, 26 February 2012 (EST)
 +
 +
== Solution 2 ==
 +
 +
Standard 3D geometry, no coordinates.
 +
 +
 +
Let the tip of the octahedron on side <math>P_1P_3</math> be <math>K_1</math> and the opposite vertex be <math>K_2</math>. Our key is to examine the trapezoid <math>P_1K_1K_2P_3</math>.
 +
 +
 +
Let the side length of the octahedron be <math>s</math>. Then <math>P_1K_1 = \frac{s}{\sqrt{2}}</math> and <math>P_3K_2 = 1 - \frac{2}{\sqrt{2}}</math>. Then, we have <math>P_1P_3 = \sqrt{2}</math>. Finally, we want to find <math>K_1K_2</math>, which is just double the height of half the octahedron. We can use Pythagorean Theorem to find that height as <math>\sqrt{2}s</math>. Now, we use the Pythagorean Theorem on the trapezoid. We get
 +
 +
<cmath>(\sqrt{2})^2 + (2\sqrt{2}-1)^2 = (s\sqrt{2})^2</cmath> <cmath>s = \frac{3\sqrt{2}}{4}.</cmath>
 +
 +
~superagh
 +
 +
==Solution 3==
 +
 +
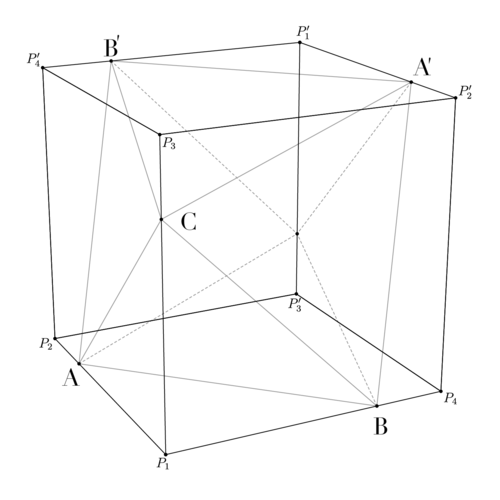
[[File:2012AMC12BProblem19Solution3.png|center|500px]]
 +
 +
Let the length of <math>P_1A = a</math>, <math>P_1B = b</math>
 +
 +
<math>AB = a^2 + b^2</math>, <math>AB' = (1-b)^2 + (1-a)^2 + 1</math>, <math>AB = AB'</math>
 +
 +
<math>a^2 + b^2 = (1-b)^2 + (1-a)^2 + 1</math>, <math>a^2 + b^2 = 1 - 2b + b^2 + 1 - 2a + a^2 + 1</math>, <math>a+ b = \frac32</math>
 +
 +
As <math>AC = BC</math>, <math>a^2 + P_1C^2 = b^2 + P_1C^2</math>, <math>a = b</math>, <math>a = \frac34</math>
 +
 +
<math>AB = \boxed{\textbf{(A) } \frac{3\sqrt{2}}{4}}</math>
 +
 +
~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]
 +
 +
== See Also ==
 +
 +
{{AMC12 box|year=2012|ab=B|num-b=18|num-a=20}}
 +
 +
[[Category:Introductory Geometry Problems]]
 +
[[Category:3D Geometry Problems]]
 +
{{MAA Notice}}

Latest revision as of 20:59, 19 September 2023

Problem

A unit cube has vertices $P_1,P_2,P_3,P_4,P_1',P_2',P_3',$ and $P_4'$. Vertices $P_2$, $P_3$, and $P_4$ are adjacent to $P_1$, and for $1\le i\le 4,$ vertices $P_i$ and $P_i'$ are opposite to each other. A regular octahedron has one vertex in each of the segments $P_1P_2$, $P_1P_3$, $P_1P_4$, $P_1'P_2'$, $P_1'P_3'$, and $P_1'P_4'$. What is the octahedron's side length?

[asy] import three; size(7.5cm); triple eye = (-4, -8, 3); currentprojection = perspective(eye); triple[] P = {(1, -1, -1), (-1, -1, -1), (-1, 1, -1), (-1, -1, 1), (1, -1, -1)}; // P[0] = P[4] for convenience triple[] Pp = {-P[0], -P[1], -P[2], -P[3], -P[4]}; // draw octahedron triple pt(int k){ return (3*P[k] + P[1])/4; } triple ptp(int k){ return (3*Pp[k] + Pp[1])/4; } draw(pt(2)--pt(3)--pt(4)--cycle, gray(0.6)); draw(ptp(2)--pt(3)--ptp(4)--cycle, gray(0.6)); draw(ptp(2)--pt(4), gray(0.6)); draw(pt(2)--ptp(4), gray(0.6)); draw(pt(4)--ptp(3)--pt(2), gray(0.6) + linetype("4 4")); draw(ptp(4)--ptp(3)--ptp(2), gray(0.6) + linetype("4 4")); // draw cube for(int i = 0; i < 4; ++i){ draw(P[1]--P[i]); draw(Pp[1]--Pp[i]); for(int j = 0; j < 4; ++j){ if(i == 1 || j == 1 || i == j) continue; draw(P[i]--Pp[j]); draw(Pp[i]--P[j]); } dot(P[i]); dot(Pp[i]); dot(pt(i)); dot(ptp(i)); } label("$P_1$", P[1], dir(P[1])); label("$P_2$", P[2], dir(P[2])); label("$P_3$", P[3], dir(-45)); label("$P_4$", P[4], dir(P[4])); label("$P'_1$", Pp[1], dir(Pp[1])); label("$P'_2$", Pp[2], dir(Pp[2])); label("$P'_3$", Pp[3], dir(-100)); label("$P'_4$", Pp[4], dir(Pp[4])); [/asy]

$\textbf{(A)}\ \frac{3\sqrt{2}}{4}\qquad\textbf{(B)}\ \frac{7\sqrt{6}}{16}\qquad\textbf{(C)}\ \frac{\sqrt{5}}{2}\qquad\textbf{(D)}\ \frac{2\sqrt{3}}{3}\qquad\textbf{(E)}\ \frac{\sqrt{6}}{2}$

Solution 1

2012 AMC-12B-19.jpg

Observe the diagram above. Each dot represents one of the six vertices of the regular octahedron. Three dots have been placed exactly x units from the $(0,0,0)$ corner of the unit cube. The other three dots have been placed exactly x units from the $(1,1,1)$ corner of the unit cube. A red square has been drawn connecting four of the dots to provide perspective regarding the shape of the octahedron. Observe that the three dots that are near $(0,0,0)$ are each $(x)(\sqrt{2}$) from each other. The same is true for the three dots that are near $(1,1,1).$ There is a unique $x$ for which the rectangle drawn in red becomes a square. This will occur when the distance from $(x,0,0)$ to $(1,1-x, 1)$ is $(x)(\sqrt{2}$).


Using the distance formula we find the distance between the two points to be: $\sqrt{{(1-x)^2} + {(1-x)^2} + 1}$ = $\sqrt{2x^2 - 4x +3}$. Equating this to $(x)(\sqrt{2}$) and squaring both sides, we have the equation:

$2{x^2} - 4x + 3$ = $2{x^2}$

$-4x + 3 = 0$

$x$ = $\frac{3} {4}$.


Since the length of each side is $(x)(\sqrt{2}$), we have a final result of $\frac{3 \sqrt{2}}{4}$. Thus, Answer choice $\boxed{\text{A}}$ is correct.


(If someone can draw a better diagram with the points labeled P1,P2, etc., I would appreciate it).

--Jm314 14:55, 26 February 2012 (EST)

Solution 2

Standard 3D geometry, no coordinates.


Let the tip of the octahedron on side $P_1P_3$ be $K_1$ and the opposite vertex be $K_2$. Our key is to examine the trapezoid $P_1K_1K_2P_3$.


Let the side length of the octahedron be $s$. Then $P_1K_1 = \frac{s}{\sqrt{2}}$ and $P_3K_2 = 1 - \frac{2}{\sqrt{2}}$. Then, we have $P_1P_3 = \sqrt{2}$. Finally, we want to find $K_1K_2$, which is just double the height of half the octahedron. We can use Pythagorean Theorem to find that height as $\sqrt{2}s$. Now, we use the Pythagorean Theorem on the trapezoid. We get

\[(\sqrt{2})^2 + (2\sqrt{2}-1)^2 = (s\sqrt{2})^2\] \[s = \frac{3\sqrt{2}}{4}.\]

~superagh

Solution 3

2012AMC12BProblem19Solution3.png

Let the length of $P_1A = a$, $P_1B = b$

$AB = a^2 + b^2$, $AB' = (1-b)^2 + (1-a)^2 + 1$, $AB = AB'$

$a^2 + b^2 = (1-b)^2 + (1-a)^2 + 1$, $a^2 + b^2 = 1 - 2b + b^2 + 1 - 2a + a^2 + 1$, $a+ b = \frac32$

As $AC = BC$, $a^2 + P_1C^2 = b^2 + P_1C^2$, $a = b$, $a = \frac34$

$AB = \boxed{\textbf{(A) } \frac{3\sqrt{2}}{4}}$

~isabelchen

See Also

2012 AMC 12B (Problems • Answer Key • Resources)
Preceded by
Problem 18 		Followed by
Problem 20
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2012_AMC_12B_Problems/Problem_19&oldid=198416"