Difference between revisions of "1985 AHSME Problems/Problem 14"
(Created page with "==Problem== Exactly three of the interior angles of a convex polygon are obtuse. What is the maximum number of sides of such a polygon? <math> \mathrm{(A)\ } 4 \qquad \mathr...") |
Sevenoptimus (talk | contribs) (Improved wording, formatting, and LaTeX) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
==Problem== | ==Problem== | ||
| − | Exactly three of the interior angles of a convex | + | Exactly three of the interior angles of a convex polygon are obtuse. What is the maximum number of sides of such a polygon? |
<math> \mathrm{(A)\ } 4 \qquad \mathrm{(B) \ }5 \qquad \mathrm{(C) \ } 6 \qquad \mathrm{(D) \ } 7 \qquad \mathrm{(E) \ }8 </math> | <math> \mathrm{(A)\ } 4 \qquad \mathrm{(B) \ }5 \qquad \mathrm{(C) \ } 6 \qquad \mathrm{(D) \ } 7 \qquad \mathrm{(E) \ }8 </math> | ||
==Solution== | ==Solution== | ||
| − | + | Suppose that such a polygon has <math>n</math> sides. Let the three obtuse angle measures, in degrees, be <math>o_1</math>, <math>o_2</math>, and <math>o_3</math> and the <math>(n-3)</math> acute angle measures, again in degrees, be <math>a_1,a_2,a_3, \dotsc a_{n-3}</math>. | |
| − | + | Since <math>90 < o_i < 180</math> for each <math>i</math>, we have <cmath>3(90) = 270 < o_1+o_2+o_3 < 3(180) = 540,</cmath> and similarly, since <math>0 < a_i < 90</math> for each <math>i</math>, <cmath>0 < a_1+a_2+a_3+\dotsb+a_{n-3} < 90(n-3) = 90n-270.</cmath> | |
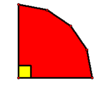
| + | It follows that <cmath>270+0 < o_1+o_2+o_3+a_1+a_2+a_3+\dotsb+a_{n-3} < 540+90n-270,</cmath> and recalling that the sum of the interior angle measures of an <math>n</math>-gon is <math>180(n-2) = 180n-360</math>, this reduces to <math>270 < 180n-360 < 90n+270</math>. Hence <cmath>\frac{540}{180} < n < \frac{270+360}{90} \iff 3 < n < 7,</cmath> so an upper bound is <math>n \leq 6</math>, and it is easy to check that this bound can be attained by e.g. a convex hexagon with a right angle, <math>2</math> acute angles, and <math>3</math> obtuse angles, as shown below: | ||
| + | [[Image: HrKCfF2ETNSQSy3uGlkg hexagonsurvey1.gif|100px]] | ||
| − | + | Accordingly, the maximum possible number of sides of such a polygon is <math>\boxed{\text{(C)} \ 6}</math>. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==See Also== | ==See Also== | ||
{{AHSME box|year=1985|num-b=13|num-a=15}} | {{AHSME box|year=1985|num-b=13|num-a=15}} | ||
| + | {{MAA Notice}} | ||
Latest revision as of 20:23, 19 March 2024
Problem
Exactly three of the interior angles of a convex polygon are obtuse. What is the maximum number of sides of such a polygon?
![]()
Solution
Suppose that such a polygon has ![]() sides. Let the three obtuse angle measures, in degrees, be
sides. Let the three obtuse angle measures, in degrees, be ![]() ,
, ![]() , and
, and ![]() and the
and the ![]() acute angle measures, again in degrees, be
acute angle measures, again in degrees, be ![]() .
.
Since ![]() for each
for each ![]() , we have
, we have ![]() and similarly, since
and similarly, since ![]() for each
for each ![]() ,
, ![]() It follows that
It follows that ![]() and recalling that the sum of the interior angle measures of an
and recalling that the sum of the interior angle measures of an ![]() -gon is
-gon is ![]() , this reduces to
, this reduces to ![]() . Hence
. Hence ![]() so an upper bound is
so an upper bound is ![]() , and it is easy to check that this bound can be attained by e.g. a convex hexagon with a right angle,
, and it is easy to check that this bound can be attained by e.g. a convex hexagon with a right angle, ![]() acute angles, and
acute angles, and ![]() obtuse angles, as shown below:
obtuse angles, as shown below:
Accordingly, the maximum possible number of sides of such a polygon is ![]() .
.
See Also
| 1985 AHSME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 13 |
Followed by Problem 15 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 | ||
| All AHSME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.