Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2011 AMC 10B Problems/Problem 25"

(formatting fixes)
m
 
(48 intermediate revisions by 23 users not shown)
Line 1: Line 1:
 
== Problem ==
 
== Problem ==
  
−
Let <math>T_1</math> be a triangle with sides <math>2011, 2012,</math> and <math>2013</math>. For <math>n \ge 1</math>, if <math>T_n = \triangle ABC</math> and <math>D, E,</math> and <math>F</math> are the points of tangency of the incircle of <math>\triangle ABC</math> to the sides <math>AB, BC</math> and <math>AC,</math> respectively, then <math>T_{n+1}</math> is a triangle with side lengths <math>AD, BE,</math> and <math>CF,</math> if it exists. What is the perimeter of the last triangle in the sequence <math>( T_n )</math>?
+
Let <math>T_1</math> be a triangle with side lengths <math>2011, 2012,</math> and <math>2013</math>. For <math>n \ge 1</math>, if <math>T_n = \triangle ABC</math> and <math>D, E,</math> and <math>F</math> are the points of tangency of the incircle of <math>\triangle ABC</math> to the sides <math>AB, BC</math>, and <math>AC,</math> respectively, then <math>T_{n+1}</math> is a triangle with side lengths <math>AD, BE,</math> and <math>CF,</math> if it exists. What is the perimeter of the last triangle in the sequence <math>( T_n )</math>?
  
 
<math> \textbf{(A)}\ \frac{1509}{8} \qquad\textbf{(B)}\ \frac{1509}{32} \qquad\textbf{(C)}\ \frac{1509}{64} \qquad\textbf{(D)}\ \frac{1509}{128} \qquad\textbf{(E)}\ \frac{1509}{256}</math>
 
<math> \textbf{(A)}\ \frac{1509}{8} \qquad\textbf{(B)}\ \frac{1509}{32} \qquad\textbf{(C)}\ \frac{1509}{64} \qquad\textbf{(D)}\ \frac{1509}{128} \qquad\textbf{(E)}\ \frac{1509}{256}</math>
 +
[[Category: Introductory Geometry Problems]]
 +
 +
==Solution 1==
 +
 +
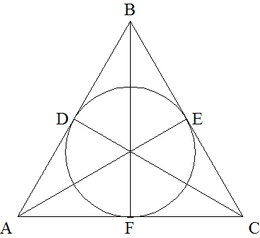
By constructing the bisectors of each angle and the perpendicular radii of the incircle the triangle consists of 3 kites.
 +
 +
[[Image:File2011AMC10B25.png|center|260px]]
 +
 +
Hence <math>AD=AF</math> and <math>BD=BE</math> and <math>CE=CF</math>. Let <math>AD = x, BD = y</math> and <math>CE = z</math> gives three equations:
 +
 +
<math>x+y = a-1</math>
 +
 +
<math>x+z = a</math>
 +
 +
<math>y+z = a+1</math>
 +
 +
(where <math>a = 2012</math> for the first triangle.)
 +
 +
Solving gives:
 +
 +
<math>x= \frac{a}{2} -1</math>
 +
 +
<math>y = \frac{a}{2}</math>
 +
 +
<math>z = \frac{a}{2}+1</math>
 +
 +
Subbing in gives that <math>T_2</math> has sides of <math>1005, 1006, 1007</math>.
 +
 +
<math>T_3</math> can easily be derived from this as the sides still differ by 1 hence the above solutions still work (now with <math>a=1006</math>). All additional triangles will differ by one as the solutions above differ by one so this process can be repeated indefinitely until the side lengths no longer form a triangle.
 +
 +
Subbing in gives <math>T_3</math> with sides <math>502, 503, 504</math>.
 +
 +
<math>T_4</math> has sides <math>\frac{501}{2}, \frac{503}{2}, \frac{505}{2}</math>.
 +
 +
<math>T_5</math> has sides <math>\frac{499}{4}, \frac{503}{4}, \frac{507}{4}</math>.
 +
 +
<math>T_6</math> has sides <math>\frac{495}{8}, \frac{503}{8}, \frac{511}{8}</math>.
 +
 +
<math>T_7</math> has sides <math>\frac{487}{16}, \frac{503}{16}, \frac{519}{16}</math>.
 +
 +
<math>T_8</math> has sides <math>\frac{471}{32}, \frac{503}{32}, \frac{535}{32}</math>.
 +
 +
<math>T_9</math> has sides <math>\frac{439}{64}, \frac{503}{64}, \frac{567}{64}</math>.
 +
 +
<math>T_{10}</math> has sides <math>\frac{375}{128}, \frac{503}{128}, \frac{631}{128}</math>.
 +
 +
<math>T_{11}</math> would have sides <math>\frac{247}{256}, \frac{503}{256}, \frac{759}{256}</math> but these lengths do not make a
 +
triangle as
 +
<cmath>\frac{247}{256} + \frac{503}{256} < \frac{759}{256}</cmath>
 +
 +
 +
Likewise, you could create an equation instead of listing all the triangles to <math>T_{11}</math>.
 +
The sides of a triangle <math>T_{k}</math> would be
 +
<cmath>\frac{503}{2^{k-3}} - 1, \frac{503}{2^{k-3}}, \frac{503}{2^{k-3}} + 1</cmath>
 +
We then have
 +
<cmath>503 - 2^{k-3} + 503 > 503 + 2^{k-3}</cmath>
 +
<cmath>1006 - 2^{k-3} > 503 + 2^{k-3}</cmath>
 +
<cmath>503 > 2^{k-2}</cmath>
 +
<cmath>9 > k-2</cmath>
 +
<cmath>k < 11</cmath>
 +
Hence, the first triangle which does not exist in this sequence is <math>T_{11}</math>.
 +
 +
Hence the perimeter is
 +
<cmath>\frac{375}{128} + \frac{503}{128} + \frac{631}{128} = \boxed{\textbf{(D)} \frac{1509}{128}}</cmath>.
 +
 +
==Solution 2==
 +
 +
Proceeding similarly to the first solution, we have that sides of each triangle are of the form <math>a, a+1, a+2</math> for some number <math>a</math>. Also, note that the perimeter of each triangle is half of the previous one. In order for the triangle to not exist, it must not satisfy the triangle inequality, meaning that <math>a + a + 1 < a+2 \Rightarrow a<1</math>. Then, the perimeter would be <math>a + a + 1 + a + 2 = 3a + 3 < 6</math>. So, to have a proper triangle, we have <math>\frac{3018}{2^{k}} > 6 \Rightarrow 2^k < 503 \Rightarrow 2^{k} < 512</math>. The first triangle to not work would have perimeter <math>\frac{3018}{256} = \frac{1509}{128}</math>,  thus the answer is  <math>\boxed{\textbf{(D)} \frac{1509}{128}}</math>.
  
−
==Solution==
 
−
{{solution}}
 
 
==See Also==
 
==See Also==
 +
Identical problem to the [[2011 AMC 12B Problems/Problem 22]].
 +
 
{{AMC10 box|year=2011|ab=B|num-b=24|after=Last Problem}}
 
{{AMC10 box|year=2011|ab=B|num-b=24|after=Last Problem}}
 +
{{MAA Notice}}

Latest revision as of 10:39, 9 November 2024

Problem

Let $T_1$ be a triangle with side lengths $2011, 2012,$ and $2013$. For $n \ge 1$, if $T_n = \triangle ABC$ and $D, E,$ and $F$ are the points of tangency of the incircle of $\triangle ABC$ to the sides $AB, BC$, and $AC,$ respectively, then $T_{n+1}$ is a triangle with side lengths $AD, BE,$ and $CF,$ if it exists. What is the perimeter of the last triangle in the sequence $( T_n )$?

$\textbf{(A)}\ \frac{1509}{8} \qquad\textbf{(B)}\ \frac{1509}{32} \qquad\textbf{(C)}\ \frac{1509}{64} \qquad\textbf{(D)}\ \frac{1509}{128} \qquad\textbf{(E)}\ \frac{1509}{256}$

Solution 1

By constructing the bisectors of each angle and the perpendicular radii of the incircle the triangle consists of 3 kites.

File2011AMC10B25.png

Hence $AD=AF$ and $BD=BE$ and $CE=CF$. Let $AD = x, BD = y$ and $CE = z$ gives three equations:

$x+y = a-1$

$x+z = a$

$y+z = a+1$

(where $a = 2012$ for the first triangle.)

Solving gives:

$x= \frac{a}{2} -1$

$y = \frac{a}{2}$

$z = \frac{a}{2}+1$

Subbing in gives that $T_2$ has sides of $1005, 1006, 1007$.

$T_3$ can easily be derived from this as the sides still differ by 1 hence the above solutions still work (now with $a=1006$). All additional triangles will differ by one as the solutions above differ by one so this process can be repeated indefinitely until the side lengths no longer form a triangle.

Subbing in gives $T_3$ with sides $502, 503, 504$.

$T_4$ has sides $\frac{501}{2}, \frac{503}{2}, \frac{505}{2}$.

$T_5$ has sides $\frac{499}{4}, \frac{503}{4}, \frac{507}{4}$.

$T_6$ has sides $\frac{495}{8}, \frac{503}{8}, \frac{511}{8}$.

$T_7$ has sides $\frac{487}{16}, \frac{503}{16}, \frac{519}{16}$.

$T_8$ has sides $\frac{471}{32}, \frac{503}{32}, \frac{535}{32}$.

$T_9$ has sides $\frac{439}{64}, \frac{503}{64}, \frac{567}{64}$.

$T_{10}$ has sides $\frac{375}{128}, \frac{503}{128}, \frac{631}{128}$.

$T_{11}$ would have sides $\frac{247}{256}, \frac{503}{256}, \frac{759}{256}$ but these lengths do not make a triangle as \[\frac{247}{256} + \frac{503}{256} < \frac{759}{256}\]


Likewise, you could create an equation instead of listing all the triangles to $T_{11}$. The sides of a triangle $T_{k}$ would be \[\frac{503}{2^{k-3}} - 1, \frac{503}{2^{k-3}}, \frac{503}{2^{k-3}} + 1\] We then have \[503 - 2^{k-3} + 503 > 503 + 2^{k-3}\] \[1006 - 2^{k-3} > 503 + 2^{k-3}\] \[503 > 2^{k-2}\] \[9 > k-2\] \[k < 11\] Hence, the first triangle which does not exist in this sequence is $T_{11}$.

Hence the perimeter is \[\frac{375}{128} + \frac{503}{128} + \frac{631}{128} = \boxed{\textbf{(D)} \frac{1509}{128}}\].

Solution 2

Proceeding similarly to the first solution, we have that sides of each triangle are of the form $a, a+1, a+2$ for some number $a$. Also, note that the perimeter of each triangle is half of the previous one. In order for the triangle to not exist, it must not satisfy the triangle inequality, meaning that $a + a + 1 < a+2 \Rightarrow a<1$. Then, the perimeter would be $a + a + 1 + a + 2 = 3a + 3 < 6$. So, to have a proper triangle, we have $\frac{3018}{2^{k}} > 6 \Rightarrow 2^k < 503 \Rightarrow 2^{k} < 512$. The first triangle to not work would have perimeter $\frac{3018}{256} = \frac{1509}{128}$, thus the answer is $\boxed{\textbf{(D)} \frac{1509}{128}}$.

See Also

Identical problem to the 2011 AMC 12B Problems/Problem 22.

2011 AMC 10B (Problems • Answer Key • Resources)
Preceded by
Problem 24 		Followed by
Last Problem
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2011_AMC_10B_Problems/Problem_25&oldid=232640"