Difference between revisions of "2008 USAMO Problems/Problem 2"

Latest revision as of 10:54, 1 May 2024

Problem

(Zuming Feng) Let $ABC$ be an acute, scalene triangle, and let $M$ , $N$ , and $P$ be the midpoints of $\overline{BC}$ , $\overline{CA}$ , and $\overline{AB}$ , respectively. Let the perpendicular bisectors of $\overline{AB}$ and $\overline{AC}$ intersect ray $AM$ in points $D$ and $E$ respectively, and let lines $BD$ and $CE$ intersect in point $F$ , inside of triangle $ABC$ . Prove that points $A$ , $N$ , $F$ , and $P$ all lie on one circle.

Solutions

Solution 1 (synthetic)

Without Loss of Generality, assume $AB >AC$ . It is sufficient to prove that $\angle OFA = 90^{\circ}$ , as this would immediately prove that $A,P,O,F,N$ are concyclic. By applying the Menelaus' Theorem in the Triangle $\triangle BFC$ for the transversal $E,M,D$ , we have (in magnitude) $\frac{FE}{EC} \cdot \frac{CM}{MB} \cdot \frac{BD}{DF} = 1 \iff \frac{FE}{EC} = \frac{DF}{BD}$ Here, we used that $BM=MC$ , as $M$ is the midpoint of $BC$ . Now, since $EC =EA$ and $BD=DA$ , we have $\frac{FE}{EA} = \frac{DF}{DA} \iff \frac{DA}{AE} = \frac{DF}{FE} \iff AF \text{ bisects exterior } \angle EFD$ Now, note that $OE$ bisects the exterior $\angle FED$ and $OD$ bisects exterior $\angle FDE$ , making $O$ the $F$ -excentre of $\triangle FED$ . This implies that $OF$ bisects interior $\angle EFD$ , making $OF \perp AF$ , as was required.

Solution 2 (complex)

Let $A=1,B=b,C=c$ where $b,c$ all lie on the unit circle. Then $O$ is 0. As noted earlier, $(FOBC)$ is cyclic. We will find the ghost point $F',$ the second intersection of $OBC$ and $ANP$ .

We know that these two circles already intersect at $O$ so we can reflect over the line between their centers. The center of $ANPO$ is the midpoint of $AO$ namely $\frac12$ . With the tangent formula and then taking the midpoint, we find that the center of $OBC$ is $\frac{bc}{b+c}.$ Then we want to find the reflection of 0 over the line through $\frac12$ and $\frac{bc}{b+c}.$ Then we get

$\begin{align*} f' &= \frac{\left(\frac{bc}{b+c}-\overline{\frac{bc}{b+c}}\right)\div2}{(1/2)-\overline{\frac{bc}{b+c}}}\\ &= \frac{\frac{bc-1}{2(b+c)}}{\frac{b+c-2}{2(b+c)}}\\ &= \frac{bc-1}{b+c-2}. \end{align*}$

Now it remains to show $\angle F'BA=\angle ABM;$ the other angle equality would follow by symmetry.

Then we get: $\begin{align*} \frac{f'-b}{b-a}\div\frac{b-a}{a-m} &=\frac{\frac{bc-1}{b+c-2}-b}{b-1}\div\frac{b-1}{1-\frac{b+c}2}\\ &=\frac{\frac{bc-1-b(b+c-2)}{b+c-2}(2-b+c)}{2(b-1)^2}\\ &=\frac{b^2-2b+1}{2(b-1)^2}\\ &=\frac12. \end{align*}$ Thus $\measuredangle F'BA=\measuredangle BAM,$ so $F'=F$ and we're done.

~cocohearts

Solution 3 (synthetic)

$[asy] /* setup and variables */ size(280); pathpen = black + linewidth(0.7); pointpen = black; pen s = fontsize(8); pair B=(0,0),C=(5,0),A=(1,4); /* A.x > C.x/2 */ /* construction and drawing */ pair P=(A+B)/2,M=(B+C)/2,N=(A+C)/2,D=IP(A--M,P--P+5*(P-bisectorpoint(A,B))),E=IP(A--M,N--N+5*(bisectorpoint(A,C)-N)),F=IP(B--B+5*(D-B),C--C+5*(E-C)),O=circumcenter(A,B,C); D(MP("A",A,(0,1),s)--MP("B",B,SW,s)--MP("C",C,SE,s)--A--MP("M",M,s)); D(B--D(MP("D",D,NE,s))--MP("P",P,(-1,0),s)--D(MP("O",O,(0,1),s))); D(D(MP("E",E,SW,s))--MP("N",N,(1,0),s)); D(C--D(MP("F",F,NW,s))); D(B--O--C,linetype("4 4")+linewidth(0.7)); D(M--N,linetype("4 4")+linewidth(0.7)); D(rightanglemark(A,P,D,3.5));D(rightanglemark(A,N,E,3.5)); D(anglemark(B,A,C)); MP("y",A,(0,-6));MP("z",A,(4,-6)); D(anglemark(B,F,C,4),linewidth(0.6));D(anglemark(B,O,C,4),linewidth(0.6)); picture p = new picture; draw(p,circumcircle(B,O,C),linetype("1 4")+linewidth(0.7)); clip(p,B+(-5,0)--B+(-5,A.y+2)--C+(5,A.y+2)--C+(5,0)--cycle); add(p); /* D(circumcircle(A,P,N),linetype("4 4")+linewidth(0.7)); */ [/asy]$

Without loss of generality $AB < AC$ . The intersection of $NE$ and $PD$ is $O$ , the circumcenter of $\triangle ABC$ .

Let $\angle BAM = y$ and $\angle CAM = z$ . Note $D$ lies on the perpendicular bisector of $AB$ , so $AD = BD$ . So $\angle FBC = \angle B - \angle ABD = B - y$ . Similarly, $\angle FCB = C - z$ , so $\angle BFC = 180 - (B + C) + (y + z) = 2A$ . Notice that $\angle BOC$ intercepts the minor arc $BC$ in the circumcircle of $\triangle ABC$ , which is double $\angle A$ . Hence $\angle BFC = \angle BOC$ , so $BFOC$ is cyclic.

Lemma. $\triangle FEO$ is directly similar to $\triangle NEM$

Proof. $\angle OFE = \angle OFC = \angle OBC = \frac {1}{2}\cdot (180 - 2A) = 90 - A$ since $F$ , $E$ , $C$ are collinear, $BFOC$ is cyclic, and $OB = OC$ . Also $\angle ENM = 90 - \angle MNC = 90 - A$ because $NE\perp AC$ , and $MNP$ is the medial triangle of $\triangle ABC$ so $AB \parallel MN$ . Hence $\angle OFE = \angle ENM$ .

Notice that $\angle AEN = 90 - z = \angle CEN$ since $NE\perp AC$ . $\angle FED = \angle MEC = 2z$ . Then $\angle FEO = \angle FED + \angle AEN = \angle CEM + \angle CEN = \angle NEM$ Hence $\angle FEO = \angle NEM$ .

Hence $\triangle FEO$ is similar to $\triangle NEM$ by AA similarity. It is easy to see that they are oriented such that they are directly similar.

End Lemma

$[asy] /* setup and variables */ size(280); pathpen = black + linewidth(0.7); pointpen = black; pen s = fontsize(8); pair B=(0,0),C=(5,0),A=(1,4); /* A.x > C.x/2 */ /* construction and drawing */ pair P=(A+B)/2,M=(B+C)/2,N=(A+C)/2,D=IP(A--M,P--P+5*(P-bisectorpoint(A,B))),E=IP(A--M,N--N+5*(bisectorpoint(A,C)-N)),F=IP(B--B+5*(D-B),C--C+5*(E-C)),O=circumcenter(A,B,C); D(MP("A",A,(0,1),s)--MP("B",B,SW,s)--MP("C",C,SE,s)--A--MP("M",M,s)); D(B--D(MP("D",D,NE,s))--MP("P",P,(-1,0),s)--D(MP("O",O,(1,0),s))); D(D(MP("E",E,SW,s))--MP("N",N,(1,0),s)); D(C--D(MP("F",F,NW,s))); D(B--O--C,linetype("4 4")+linewidth(0.7)); D(F--N); D(O--M); D(rightanglemark(A,P,D,3.5));D(rightanglemark(A,N,E,3.5)); /* commented in above asy D(circumcircle(A,P,N),linetype("4 4")+linewidth(0.7)); D(anglemark(B,A,C)); MP("y",A,(0,-6));MP("z",A,(4,-6)); D(anglemark(B,F,C,4),linewidth(0.6));D(anglemark(B,O,C,4),linewidth(0.6)); picture p = new picture; draw(p,circumcircle(B,O,C),linetype("1 4")+linewidth(0.7)); clip(p,B+(-5,0)--B+(-5,A.y+2)--C+(5,A.y+2)--C+(5,0)--cycle); add(p); */ [/asy]$

By the similarity in the Lemma, $FE: EO = NE: EM\implies FE: EN = OE: EM$ . $\angle FEN = \angle OEM$ so $\triangle FEN\sim\triangle OEM$ by SAS similarity. Hence $\angle EMO = \angle ENF = \angle ONF$ Using essentially the same angle chasing, we can show that $\triangle PDM$ is directly similar to $\triangle FDO$ . It follows that $\triangle PDF$ is directly similar to $\triangle MDO$ . So $\angle EMO = \angle DMO = \angle DPF = \angle OPF$ Hence $\angle OPF = \angle ONF$ , so $FONP$ is cyclic. In other words, $F$ lies on the circumcircle of $\triangle PON$ . Note that $\angle ONA = \angle OPA = 90$ , so $APON$ is cyclic. In other words, $A$ lies on the circumcircle of $\triangle PON$ . $A$ , $P$ , $N$ , $O$ , and $F$ all lie on the circumcircle of $\triangle PON$ . Hence $A$ , $P$ , $F$ , and $N$ lie on a circle, as desired.

Solution 4 (synthetic)

This solution utilizes the phantom point method. Clearly, APON are cyclic because $\angle OPA = \angle ONA = 90$ . Let the circumcircles of triangles $APN$ and $BOC$ intersect at $F'$ and $O$ .

Lemma. If $A,B,C$ are points on circle $\omega$ with center $O$ , and the tangents to $\omega$ at $B,C$ intersect at $Q$ , then $AP$ is the symmedian from $A$ to $BC$ .

Proof. This is fairly easy to prove (as H, O are isogonal conjugates, plus using SAS similarity), but the author lacks time to write it up fully, and will do so soon.

End Lemma

It is easy to see $Q$ (the intersection of ray $OM$ and the circumcircle of $\triangle BOC$ ) is colinear with $A$ and $F'$ , and because line $OM$ is the diameter of that circle, $\angle QBO = \angle QCO = 90$ , so $Q$ is the point $Q$ in the lemma; hence, we may apply the lemma. From here, it is simple angle-chasing to show that $F'$ satisfies the original construction for $F$ , showing $F=F'$ ; we are done.

Solution 5 (trigonometric)

By the Law of Sines, $\frac {\sin\angle BAM}{\sin\angle CAM} = \frac {\sin B}{\sin C} = \frac bc = \frac {b/AF}{c/AF} = \frac {\sin\angle AFC\cdot\sin\angle ABF}{\sin\angle ACF\cdot\sin\angle AFB}$ . Since $\angle ABF = \angle ABD = \angle BAD = \angle BAM$ and similarly $\angle ACF = \angle CAM$ , we cancel to get $\sin\angle AFC = \sin\angle AFB$ . Obviously, $\angle AFB + \angle AFC > 180^\circ$ so $\angle AFC = \angle AFB$ .

Then $\angle FAB + \angle ABF = 180^\circ - \angle AFB = 180^\circ - \angle AFC = \angle FAC + \angle ACF$ and $\angle ABF + \angle ACF = \angle A = \angle FAB + \angle FAC$ . Subtracting these two equations, $\angle FAB - \angle FCA = \angle FCA - \angle FAB$ so $\angle BAF = \angle ACF$ . Therefore, $\triangle ABF\sim\triangle CAF$ (by AA similarity), so a spiral similarity centered at $F$ takes $B$ to $A$ and $A$ to $C$ . Therefore, it takes the midpoint of $\overline{BA}$ to the midpoint of $\overline{AC}$ , or $P$ to $N$ . So $\angle APF = \angle CNF = 180^\circ - \angle ANF$ and $APFN$ is cyclic.

Solution 6 (isogonal conjugates)

$[asy] /* setup and variables */ size(280); pathpen = black + linewidth(0.7); pointpen = black; pen s = fontsize(8); pair B=(0,0),C=(5,0),A=(4,4); /* A.x > C.x/2 */ /* construction and drawing */ pair P=(A+B)/2,M=(B+C)/2,N=(A+C)/2,D=IP(A--M,P--P+5*(P-bisectorpoint(A,B))),E=IP(A--M,N--N+5*(bisectorpoint(A,C)-N)),F=IP(B--B+5*(D-B),C--C+5*(E-C)),O=circumcenter(A,B,C); D(MP("A",A,(0,1),s)--MP("B",B,SW,s)--MP("C",C,SE,s)--A--MP("M",M,s)); D(C--D(MP("E",E,NW,s))--MP("N",N,(1,0),s)--D(MP("O",O,SW,s))); D(D(MP("D",D,SE,s))--MP("P",P,W,s)); D(B--D(MP("F",F,s))); D(O--A--F,linetype("4 4")+linewidth(0.7)); D(MP("O'",circumcenter(A,P,N),NW,s)); D(circumcircle(A,P,N),linetype("4 4")+linewidth(0.7)); D(rightanglemark(A,P,D,3.5));D(rightanglemark(A,N,E,3.5)); picture p = new picture; draw(p,circumcircle(B,O,C),linetype("1 4")+linewidth(0.7)); draw(p,circumcircle(A,B,C),linetype("1 4")+linewidth(0.7)); clip(p,B+(-5,0)--B+(-5,A.y+2)--C+(5,A.y+2)--C+(5,0)--cycle); add(p); [/asy]$

Construct $T$ on $AM$ such that $\angle BCT = \angle ACF$ . Then $\angle BCT = \angle CAM$ . Then $\triangle AMC\sim\triangle CMT$ , so $\frac {AM}{CM} = \frac {CM}{TM}$ , or $\frac {AM}{BM} = \frac {BM}{TM}$ . Then $\triangle AMB\sim\triangle BMT$ , so $\angle CBT = \angle BAM = \angle FBA$ . Then we have

$\angle CBT = \angle ABF$ and $\angle BCT = \angle ACF$ . So $T$ and $F$ are isogonally conjugate. Thus $\angle BAF = \angle CAM$ . Then

$\angle AFB = 180 - \angle ABF - \angle BAF = 180 - \angle BAM - \angle CAM = 180 - \angle BAC$ .

If $O$ is the circumcenter of $\triangle ABC$ then $\angle BFC = 2\angle BAC = \angle BOC$ so $BFOC$ is cyclic. Then $\angle BFO = 180 - \angle BOC = 180 - (90 - \angle BAC) = 90 + \angle BAC$ .

Then $\angle AFO = 360 - \angle AFB - \angle BFO = 360 - (180 - \angle BAC) - (90 + \angle BAC) = 90$ . Then $\triangle AFO$ is a right triangle.

Now by the homothety centered at $A$ with ratio $\frac {1}{2}$ , $B$ is taken to $P$ and $C$ is taken to $N$ . Thus $O$ is taken to the circumcenter of $\triangle APN$ and is the midpoint of $AO$ , which is also the circumcenter of $\triangle AFO$ , so $A,P,N,F,O$ all lie on a circle.

Solution 7 (symmedians)

Median $AM$ of a triangle $ABC$ implies $\frac {\sin{BAM}}{\sin{CAM}} = \frac {\sin{B}}{\sin{C}}$ . Trig ceva for $F$ shows that $AF$ is a symmedian. Then $FP$ is a median, use the lemma again to show that $AFP = C$ , and similarly $AFN = B$ , so you're done.

Solution 8 (inversion) (Official Solution #2)

Invert the figure about a circle centered at $A$ , and let $X'$ denote the image of the point $X$ under this inversion. Find point $F_1'$ so that $AB'F_1'C'$ is a parallelogram and let $Z'$ denote the center of this parallelogram. Note that $\triangle BAC\sim\triangle C'AB'$ and $\triangle BAD\sim\triangle D'AB'$ . Because $M$ is the midpoint of $BC$ and $Z'$ is the midpoint of $B'C'$ , we also have $\triangle BAM\sim\triangle C'AZ'$ . Thus $\angle AF_1'B' = \angle F_1'AC' = \angle Z'AC' = \angle MAB = \angle DAB = \angle DBA = \angle AD'B'.$ Hence quadrilateral $AB'D'F_1'$ is cyclic and, by a similar argument, quadrilateral $AC'E'F_1'$ is also cyclic. Because the images under the inversion of lines $BDF$ and $CFE$ are circles that intersect in $A$ and $F'$ , it follows that $F_1' = F'$ .

Next note that $B'$ , $Z'$ , and $C'$ are collinear and are the images of $P'$ , $F'$ , and $N'$ , respectively, under a homothety centered at $A$ and with ratio $1/2$ . It follows that $P'$ , $F'$ , and $N'$ are collinear, and then that the points $A$ , $P$ , $F$ , and $N$ lie on a circle.

Solution 9 (Official Solution #1)

Let $O$ be the circumcenter of triangle $ABC$ . We prove that $\angle APO = \angle ANO = \angle AFO = 90^\circ.\qquad\qquad (1)$ It will then follow that $A, P, O, F, N$ lie on the circle with diameter $\overline{AO}$ . Indeed, the fact that the first two angles in $(1)$ are right is immediate because $\overline{OP}$ and $\overline{ON}$ are the perpendicular bisectors of $\overline{AB}$ and $\overline{AC}$ , respectively. Thus we need only prove that $\angle AFO = 90^\circ$ .

We may assume, without loss of generality, that $AB > AC$ . This leads to configurations similar to the ones shown above. The proof can be adapted to other configurations. Because $\overline{PO}$ is the perpendicular bisector of $\overline{AB}$ , it follows that triangle $ADB$ is an isosceles triangle with $AD = BD$ . Likewise, triangle $AEC$ is isosceles with $AE = CE$ . Let $x = \angle ABD = \angle BAD$ and $y = \angle CAE = \angle ACE$ , so $x + y = \angle BAC$ .

Applying the Law of Sines to triangles $ABM$ and $ACM$ gives $\frac{BM}{\sin x} = \frac{AB}{\sin\angle BMA}\quad\text{and}\quad\frac{CM}{\sin y} = \frac{AC}{\sin\angle CMA}.$ Taking the quotient of the two equations and noting that $\sin\angle BMA = \sin\angle CMA$ , we find $\frac{BM}{CM}\frac{\sin y}{\sin x} = \frac{AB}{AC}\frac{\sin\angle CMA}{\sin\angle BMA} = \frac{AB}{AC}.$ Because $BM = MC$ , we have $\frac{\sin x}{\sin y} = \frac{AC}{AB}.\qquad\qquad (2)$ Applying the Law of Sines to triangles $ABF$ and $ACF$ , we find $\frac{AF}{\sin x} = \frac{AB}{\sin\angle AFB}\quad\text{and}\quad\frac{AF}{\sin y} = \frac{AC}{\sin\angle AFC}.$ Taking the quotient of the two equations yields $\frac{\sin x}{\sin y} = \frac{AC}{AB}\frac{\sin\angle AFB}{\sin\angle AFC},$ so by $(2)$ , $\sin\angle AFB = \sin\angle AFC.\qquad\qquad (3)$ Because $\angle ADF$ is an exterior angle to triangle $ADB$ , we have $\angle EDF = 2x$ . Similarly, $\angle DEF = 2y$ . Hence $\angle EFD = 180^\circ - 2x - 2y = 180^\circ - 2\angle BAC.$ Thus $\angle BFC = 2\angle BAC = \angle BOC$ , so $BOFC$ is cyclic. In addition, $\angle AFB + \angle AFC = 360^\circ - 2\angle BAC > 180^\circ,$ and hence, from $(3)$ , $\angle AFB = \angle AFC = 180^\circ - \angle BAC$ . Because $BOFC$ is cyclic and $\triangle BOC$ is isosceles with vertex angle $\angle BOC = 2\angle BAC$ , we have $\angle OFB = \angle OCB = 90^\circ - \angle BAC$ . Therefore, $\angle AFO = \angle AFB - \angle OFB = (180^\circ - \angle BAC) - (90^\circ - \angle BAC) = 90^\circ.$ This completes the proof.

Solution 10 (Anti-Steiner point)

First, let $O$ be the circumcenter of $\triangle{ABC}$ . Note that since $AP \perp PO$ and $AN \perp NO$ , then $A$ , $N$ , $O$ and $P$ , are concyclic.

Notice that $NM \parallel AB$ and $AB \perp PO$ , which means $NM \perp PO$ . It follows analogously that $PM \perp NO$ . This means that $M$ is the orthocenter of triangle ${NOP}$ .

Now consider what happens when we reflect line $AM$ over line $PO$ . Since $PO$ is just the perpendicular bisector of $AB$ , point $A$ will map to point $B$ , and point $D$ , which is both line $AM$ and $PO$ , will map to itself. Therefore, we get line $BD$ from this reflection. It follows analogously that by reflecting line $AM$ over line $NO$ , we get $CE$ .

Since line $AM$ passes through $M$ , the orthocenter of triangle ${NOP}$ , its reflections over sides $PO$ and $NO$ , which correspond to $BD$ and $CE$ respectively, intersect on $\odot{NOP}$ (this is the Anti-Steiner point application). Therefore, $F$ , the intersection of $BD$ and $CE$ , lies on $\odot{NOP}$ .

Since $A$ , $N$ , $O$ , and $P$ are concyclic, then $\odot{NOP}$ is the same as $\odot{ANP}$ , so $F$ lies on $\odot{ANP}$ , which is the same as saying $A$ , $N$ , $F$ , and $P$ are concyclic, as desired.

Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.

@@ Line 2: / Line 2: @@
 (''Zuming Feng'') Let <math>ABC</math> be an acute, [[scalene]] triangle, and let <math>M</math>, <math>N</math>, and <math>P</math> be the midpoints of <math>\overline{BC}</math>, <math>\overline{CA}</math>, and <math>\overline{AB}</math>, respectively. Let the [[perpendicular]] [[bisect]]ors of <math>\overline{AB}</math> and <math>\overline{AC}</math> intersect ray <math>AM</math> in points <math>D</math> and <math>E</math> respectively, and let lines <math>BD</math> and <math>CE</math> intersect in point <math>F</math>, inside of triangle <math>ABC</math>. Prove that points <math>A</math>, <math>N</math>, <math>F</math>, and <math>P</math> all lie on one circle.
-__TOC__
+== Solutions ==
-== Solution ==
 === Solution 1 (synthetic) ===
+Without Loss of Generality, assume <math>AB >AC</math>. It is sufficient to prove that <math>\angle OFA = 90^{\circ}</math>, as this would immediately prove that <math>A,P,O,F,N</math> are concyclic.
+By applying the Menelaus' Theorem in the Triangle <math>\triangle BFC</math> for the transversal <math>E,M,D</math>, we have (in magnitude)
+<cmath> \frac{FE}{EC} \cdot \frac{CM}{MB} \cdot \frac{BD}{DF} = 1 \iff \frac{FE}{EC} = \frac{DF}{BD}
+</cmath>
+Here, we used that <math>BM=MC</math>, as <math>M</math> is the midpoint of <math>BC</math>. Now, since <math>EC =EA</math> and <math>BD=DA</math>, we have
+<cmath> \frac{FE}{EA} = \frac{DF}{DA} \iff \frac{DA}{AE} = \frac{DF}{FE} \iff AF \text{ bisects exterior } \angle EFD
+</cmath>
+Now, note that <math>OE</math> bisects the exterior <math>\angle FED</math> and <math>OD</math> bisects exterior <math>\angle FDE</math>, making <math>O</math> the <math>F</math>-excentre of <math>\triangle FED</math>. This implies that <math>OF</math> bisects interior <math>\angle EFD</math>, making <math>OF \perp AF</math>, as was required.
+=== Solution 2 (complex) ===
+Let <math>A=1,B=b,C=c</math> where <math>b,c</math> all lie on the unit circle. Then <math>O</math> is 0. As noted earlier, <math>(FOBC)</math> is cyclic. We will find the ghost point <math>F',</math> the second intersection of <math>OBC</math> and <math>ANP</math>.
+We know that these two circles already intersect at <math>O</math> so we can reflect over the line between their centers. The center of <math>ANPO</math> is the midpoint of <math>AO</math> namely <math>\frac12</math>. With the tangent formula and then taking the midpoint, we find that the center of <math>OBC</math> is <math>\frac{bc}{b+c}.</math> Then we want to find the reflection of 0 over the line through <math>\frac12</math> and <math>\frac{bc}{b+c}.</math> Then we get
+<cmath> \begin{align*}
+f' &= \frac{\left(\frac{bc}{b+c}-\overline{\frac{bc}{b+c}}\right)\div2}{(1/2)-\overline{\frac{bc}{b+c}}}\\
+&= \frac{\frac{bc-1}{2(b+c)}}{\frac{b+c-2}{2(b+c)}}\\
+&= \frac{bc-1}{b+c-2}.
+\end{align*} </cmath>
+Now it remains to show <math>\angle F'BA=\angle ABM;</math> the other angle equality would follow by symmetry.
+Then we get:
+<cmath> \begin{align*}
+\frac{f'-b}{b-a}\div\frac{b-a}{a-m}
+&=\frac{\frac{bc-1}{b+c-2}-b}{b-1}\div\frac{b-1}{1-\frac{b+c}2}\\
+&=\frac{\frac{bc-1-b(b+c-2)}{b+c-2}(2-b+c)}{2(b-1)^2}\\
+&=\frac{b^2-2b+1}{2(b-1)^2}\\
+&=\frac12.
+\end{align*} </cmath>
+Thus <math>\measuredangle F'BA=\measuredangle BAM,</math> so <math>F'=F</math> and we're done.
+~cocohearts
+=== Solution 3 (synthetic) ===
 <center><asy>
    /* setup and variables */
@@ Line 32: / Line 68: @@
 Let <math>\angle BAM = y</math> and <math>\angle CAM = z</math>. Note <math>D</math> lies on the perpendicular bisector of <math>AB</math>, so <math>AD = BD</math>. So <math>\angle FBC = \angle B - \angle ABD = B - y</math>. Similarly, <math>\angle FCB = C - z</math>, so <math>\angle BFC = 180 - (B + C) + (y + z) = 2A</math>. Notice that <math>\angle BOC</math> intercepts the minor arc <math>BC</math> in the [[circumcircle]] of <math>\triangle ABC</math>, which is double <math>\angle A</math>. Hence <math>\angle BFC = \angle BOC</math>, so <math>BFOC</math> is cyclic.
+'''Lemma.''' <math>\triangle FEO</math> is directly similar to <math>\triangle NEM</math>
-====Lemma 1====
+''Proof.''
-<math>\triangle FEO</math> is directly similar to <math>\triangle NEM</math>
+<cmath>\angle OFE = \angle OFC = \angle OBC = \frac {1}{2}\cdot (180 - 2A) = 90 - A</cmath>
-<cmath>
-\angle OFE = \angle OFC = \angle OBC = \frac {1}{2}\cdot (180 - 2A) = 90 - A
-</cmath>
 since <math>F</math>, <math>E</math>, <math>C</math> are collinear, <math>BFOC</math> is cyclic, and <math>OB = OC</math>. Also
-<cmath>
+<cmath>\angle ENM = 90 - \angle MNC = 90 - A</cmath>
-\angle ENM = 90 - \angle MNC = 90 - A
-</cmath>
 because <math>NE\perp AC</math>, and <math>MNP</math> is the medial triangle of <math>\triangle ABC</math> so <math>AB \parallel MN</math>. Hence <math>\angle OFE = \angle ENM</math>.
-Notice that <math>\angle AEN = 90 - z = \angle CEN</math> since <math>NE\perp BC</math>. <math>\angle FED = \angle MEC = 2z</math>. Then
+Notice that <math>\angle AEN = 90 - z = \angle CEN</math> since <math>NE\perp AC</math>. <math>\angle FED = \angle MEC = 2z</math>. Then
-<cmath>
+<cmath>\angle FEO = \angle FED + \angle AEN = \angle CEM + \angle CEN = \angle NEM</cmath>
-\angle FEO = \angle FED + \angle AEN = \angle CEM + \angle CEN = \angle NEM
-</cmath>
 Hence <math>\angle FEO = \angle NEM</math>.
 Hence <math>\triangle FEO</math> is similar to <math>\triangle NEM</math> by AA similarity. It is easy to see that they are oriented such that they are directly similar.
-====Lemma 2====
+'''End Lemma'''
 <center><asy>
@@ Line 69: / Line 99: @@
 D(rightanglemark(A,P,D,3.5));D(rightanglemark(A,N,E,3.5));
-/* commented from above asy */
+/* commented in above asy
 D(circumcircle(A,P,N),linetype("4 4")+linewidth(0.7));
 D(anglemark(B,A,C)); MP("y",A,(0,-6));MP("z",A,(4,-6));
@@ Line 76: / Line 106: @@
 draw(p,circumcircle(B,O,C),linetype("1 4")+linewidth(0.7));
 clip(p,B+(-5,0)--B+(-5,A.y+2)--C+(5,A.y+2)--C+(5,0)--cycle); add(p);
+*/
 </asy></center>
-By the similarity in Lemma 1, <math>FE: EO = NE: EM\implies FE: EN = OE: EM</math>. <math>\angle FEN = \angle OEM</math> so <math>\triangle FEN\sim\triangle OEM</math> by SAS similarity. Hence
+By the similarity in the Lemma, <math>FE: EO = NE: EM\implies FE: EN = OE: EM</math>. <math>\angle FEN = \angle OEM</math> so <math>\triangle FEN\sim\triangle OEM</math> by SAS similarity. Hence
-<cmath>
+<cmath>\angle EMO = \angle ENF = \angle ONF</cmath>
-\angle EMO = \angle ENF = \angle ONF
+Using essentially the same angle chasing, we can show that <math>\triangle PDM</math> is directly similar to <math>\triangle FDO</math>. It follows that <math>\triangle PDF</math> is directly similar to <math>\triangle MDO</math>. So
-</cmath>
+<cmath>\angle EMO = \angle DMO = \angle DPF = \angle OPF</cmath>
-Using essentially the same angle chasing, we can show that <math>\triangle PDM</math> is directly similar to <math>\triangle FMO</math>. It follows that <math>\triangle PDF</math> is directly similar to <math>MDO</math>. So
-<cmath>
-\angle EMO = \angle DMO = \angle DPF = \angle OPF
-</cmath>
 Hence <math>\angle OPF = \angle ONF</math>, so <math>FONP</math> is cyclic. In other words, <math>F</math> lies on the circumcircle of <math>\triangle PON</math>. Note that <math>\angle ONA = \angle OPA = 90</math>, so <math>APON</math> is cyclic. In other words, <math>A</math> lies on the circumcircle of <math>\triangle PON</math>. <math>A</math>, <math>P</math>, <math>N</math>, <math>O</math>, and <math>F</math> all lie on the circumcircle of <math>\triangle PON</math>. Hence <math>A</math>, <math>P</math>, <math>F</math>, and <math>N</math> lie on a circle, as desired.
-=== Solution 2 (synthetic) ===
+=== Solution 4 (synthetic) ===
-Without Loss of Generality, assume <math>AB >AC</math>. It is sufficient to prove that <math>\angle OFA = 90^{\circ}</math>, as this would immediately prove that <math>A,P,O,F,N</math> are concyclic.
+This solution utilizes the ''phantom point method.'' Clearly, APON are cyclic because <math>\angle OPA = \angle ONA = 90</math>. Let the circumcircles of triangles <math>APN</math> and <math>BOC</math> intersect at <math>F'</math> and <math>O</math>.
-By applying the Menelaus' Theorem in the Triangle <math>\triangle BFC</math> for the transversal <math>E,M,D</math>, we have (in magnitude)
-<cmath> \frac{FE}{EC} \cdot \frac{CM}{MB} \cdot \frac{BD}{DF} = 1 \iff \frac{FE}{EC} = \frac{DF}{BD}
+'''Lemma.''' If <math>A,B,C</math> are points on circle <math>\omega</math> with center <math>O</math>, and the tangents to <math>\omega</math> at <math>B,C</math> intersect at <math>Q</math>, then <math>AP</math> is the symmedian from <math>A</math> to <math>BC</math>.
-</cmath>
-Here, we used that <math>BM=MC</math>, as <math>M</math> is the midpoint of <math>BC</math>. Now, since <math>EC =EA</math> and <math>BD=DA</math>, we have
-<cmath> \frac{FE}{EA} = \frac{DF}{DA} \iff \frac{DA}{AE} = \frac{DF}{FE} \iff AF \text{ bisects exterior } \angle EFD
-</cmath>
-Now, note that <math>OE</math> bisects the exterior <math>\angle FED</math> and <math>OD</math> bisects exterior <math>\angle FDE</math>, making <math>O</math> the <math>F</math>-excentre of <math>\triangle FED</math>. This implies that <math>OF</math> bisects interior <math>\angle EFD</math>, making <math>OF \perp AF</math>, as was required.
-=== Solution 3 (synthetic) ===
+''Proof.'' This is fairly easy to prove (as H, O are isogonal conjugates, plus using SAS similarity), but the author lacks time to write it up fully, and will do so soon.
-Hint: consider <math>CF</math> intersection with <math>PM</math>; show that the resulting intersection lies on the desired circle. {{incomplete|solution}}
-=== Solution 4 (synthetic) ===
+'''End Lemma'''
-This solution utilizes the ''phantom point method.'' Clearly, APON are cyclic because <math>\angle OPA = \angle ONA = 90</math>. Let the circumcircles of triangles <math>APN</math> and <math>BOC</math> intersect at <math>F'</math> and <math>O</math>.
-Lemma. If <math>A,B,C</math> are points on circle <math>\omega</math> with center <math>O</math>, and the tangents to <math>\omega</math> at <math>B,C</math> intersect at <math>Q</math>, then <math>AP</math> is the symmedian from <math>A</math> to <math>BC</math>.
+It is easy to see <math>Q</math> (the intersection of ray <math>OM</math> and the circumcircle of <math>\triangle BOC</math>) is colinear with <math>A</math> and <math>F'</math>, and because line <math>OM</math> is the diameter of that circle, <math>\angle QBO = \angle QCO = 90</math>, so <math>Q</math> is the point <math>Q</math> in the lemma; hence, we may apply the lemma. From here, it is simple angle-chasing to show that <math>F'</math> satisfies the original construction for <math>F</math>, showing <math>F=F'</math>; we are done.
-This is fairly easy to prove (as H, O are isogonal conjugates, plus using SAS similarity), but the author lacks time to write it up fully, and will do so soon.
-It is easy to see <math>Q</math> (the intersection of ray <math>OM</math> and the circumcircle of <math>\triangle BOC</math>) is colinear with <math>A</math> and <math>F'</math>, and because line <math>OM</math> is the diameter of that circle, <math>\angle QBO = \angle QCO = 90</math>, so <math>Q</math> is the point <math>Q</math> in the lemma; hence, we may apply the lemma. From here, it is simple angle-chasing to show that <math>F'</math> satisfies the original construction for <math>F</math>, showing <math>F=F'</math>; we are done. {{incomplete|solution}}
 === Solution 5 (trigonometric) ===
@@ Line 152: / Line 169: @@
 Median <math>AM</math> of a triangle <math>ABC</math> implies <math>\frac {\sin{BAM}}{\sin{CAM}} = \frac {\sin{B}}{\sin{C}}</math>.
 Trig ceva for <math>F</math> shows that <math>AF</math> is a symmedian.
-Then <math>FP</math> is a median, use the lemma again to show that <math>AFP = C</math>, and similarly <math>AFN = B</math>, so you're done. {{incomplete|solution}}
+Then <math>FP</math> is a median, use the lemma again to show that <math>AFP = C</math>, and similarly <math>AFN = B</math>, so you're done.
+=== Solution 8 (inversion) (Official Solution #2) ===
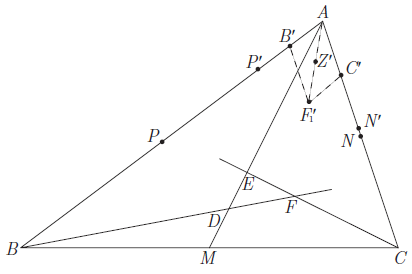
+Invert the figure about a circle centered at <math>A</math>, and let <math>X'</math> denote the image of the point <math>X</math> under this inversion. Find point <math>F_1'</math> so that <math>AB'F_1'C'</math> is a parallelogram and let <math>Z'</math> denote the center of this parallelogram. Note that <math>\triangle BAC\sim\triangle C'AB'</math> and <math>\triangle BAD\sim\triangle D'AB'</math>. Because <math>M</math> is the midpoint of <math>BC</math> and <math>Z'</math> is the midpoint of <math>B'C'</math>, we also have <math>\triangle BAM\sim\triangle C'AZ'</math>. Thus
+<cmath>\angle AF_1'B' = \angle F_1'AC' = \angle Z'AC' = \angle MAB = \angle DAB = \angle DBA = \angle AD'B'.</cmath>
+Hence quadrilateral <math>AB'D'F_1'</math> is cyclic and, by a similar argument, quadrilateral <math>AC'E'F_1'</math> is also cyclic. Because the images under the inversion of lines <math>BDF</math> and <math>CFE</math> are circles that intersect in <math>A</math> and <math>F'</math>, it follows that <math>F_1' = F'</math>.
+Next note that <math>B'</math>, <math>Z'</math>, and <math>C'</math> are collinear and are the images of <math>P'</math>, <math>F'</math>, and <math>N'</math>, respectively, under a homothety centered at <math>A</math> and with ratio <math>1/2</math>. It follows that <math>P'</math>, <math>F'</math>, and <math>N'</math> are collinear, and then that the points <math>A</math>, <math>P</math>, <math>F</math>, and <math>N</math> lie on a circle.
+<center>[[File:2008usamo2-sol8.png]]</center>
+=== Solution 9 (Official Solution #1)===
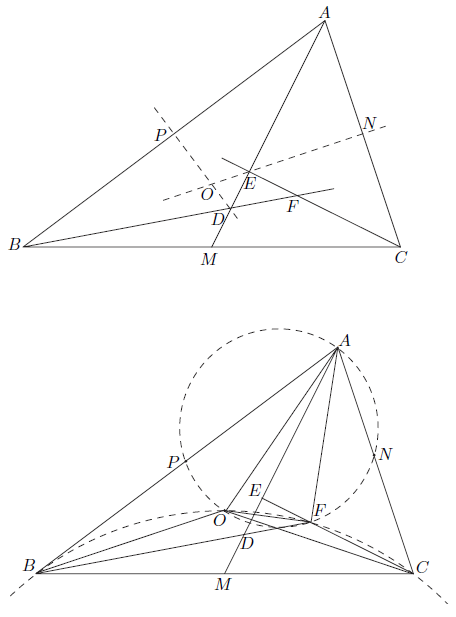
+Let <math>O</math> be the circumcenter of triangle <math>ABC</math>. We prove that
+<cmath>\angle APO = \angle ANO = \angle AFO = 90^\circ.\qquad\qquad (1)</cmath>
+It will then follow that <math>A, P, O, F, N</math> lie on the circle with diameter <math>\overline{AO}</math>. Indeed, the fact that the first two angles in <math>(1)</math> are right is immediate because <math>\overline{OP}</math> and <math>\overline{ON}</math> are the perpendicular bisectors of <math>\overline{AB}</math> and <math>\overline{AC}</math>, respectively. Thus we need only prove that <math>\angle AFO = 90^\circ</math>.
+<center>[[File:2008usamo2-sol9.png]]</center>
+We may assume, without loss of generality, that <math>AB > AC</math>. This leads to configurations similar to the ones shown above. The proof can be adapted to other configurations. Because <math>\overline{PO}</math> is the perpendicular bisector of <math>\overline{AB}</math>, it follows that triangle <math>ADB</math> is an isosceles triangle with <math>AD = BD</math>. Likewise, triangle <math>AEC</math> is isosceles with <math>AE = CE</math>. Let <math>x = \angle ABD = \angle BAD</math> and <math>y = \angle CAE = \angle ACE</math>, so <math>x + y = \angle BAC</math>.
+Applying the Law of Sines to triangles <math>ABM</math> and <math>ACM</math> gives
+<cmath>\frac{BM}{\sin x} = \frac{AB}{\sin\angle BMA}\quad\text{and}\quad\frac{CM}{\sin y} = \frac{AC}{\sin\angle CMA}.</cmath>
+Taking the quotient of the two equations and noting that <math>\sin\angle BMA = \sin\angle CMA</math>, we find
+<cmath>\frac{BM}{CM}\frac{\sin y}{\sin x} = \frac{AB}{AC}\frac{\sin\angle CMA}{\sin\angle BMA} = \frac{AB}{AC}.</cmath>
+Because <math>BM = MC</math>, we have
+<cmath>\frac{\sin x}{\sin y} = \frac{AC}{AB}.\qquad\qquad (2)</cmath>
+Applying the Law of Sines to triangles <math>ABF</math> and <math>ACF</math>, we find
+<cmath>\frac{AF}{\sin x} = \frac{AB}{\sin\angle AFB}\quad\text{and}\quad\frac{AF}{\sin y} = \frac{AC}{\sin\angle AFC}.</cmath>
+Taking the quotient of the two equations yields
+<cmath>\frac{\sin x}{\sin y} = \frac{AC}{AB}\frac{\sin\angle AFB}{\sin\angle AFC},</cmath>
+so by <math>(2)</math>,
+<cmath>\sin\angle AFB = \sin\angle AFC.\qquad\qquad (3)</cmath>
+Because <math>\angle ADF</math> is an exterior angle to triangle <math>ADB</math>, we have <math>\angle EDF = 2x</math>. Similarly, <math>\angle DEF = 2y</math>. Hence
+<cmath>\angle EFD = 180^\circ - 2x - 2y = 180^\circ - 2\angle BAC.</cmath>
+Thus <math>\angle BFC = 2\angle BAC = \angle BOC</math>, so <math>BOFC</math> is cyclic. In addition,
+<cmath>\angle AFB + \angle AFC = 360^\circ - 2\angle BAC > 180^\circ,</cmath>
+and hence, from <math>(3)</math>, <math>\angle AFB = \angle AFC = 180^\circ - \angle BAC</math>. Because <math>BOFC</math> is cyclic and <math>\triangle BOC</math> is isosceles with vertex angle <math>\angle BOC = 2\angle BAC</math>, we have <math>\angle OFB = \angle OCB = 90^\circ - \angle BAC</math>. Therefore,
+<cmath>\angle AFO = \angle AFB - \angle OFB = (180^\circ - \angle BAC) - (90^\circ - \angle BAC) = 90^\circ.</cmath>
+This completes the proof.
+=== Solution 10 (Anti-Steiner point) ===
+First, let <math>O</math> be the circumcenter of <math>\triangle{ABC}</math>. Note that since <math>AP \perp PO</math> and <math>AN \perp NO</math>, then <math>A</math>, <math>N</math>, <math>O</math> and <math>P</math>, are concyclic.
+Notice that <math>NM \parallel AB</math> and <math>AB \perp PO</math>, which means <math>NM \perp PO</math>. It follows analogously that <math>PM \perp NO</math>. This means that <math>M</math> is the orthocenter of triangle <math>{NOP}</math>.
-=== Solution 8 (inversion) ===
+Now consider what happens when we reflect line <math>AM</math> over line <math>PO</math>. Since <math>PO</math> is just the perpendicular bisector of <math>AB</math>, point <math>A</math> will map to point <math>B</math>, and point <math>D</math>, which is both line <math>AM</math> and <math>PO</math>, will map to itself. Therefore, we get line <math>BD</math> from this reflection. It follows analogously that by reflecting line <math>AM</math> over line <math>NO</math>, we get <math>CE</math>.
-<center><asy>
-size(280);
-pathpen = black + linewidth(0.7); pointpen = black; pen s = fontsize(8);
-pair B=(0,0),C=(5,0),A=(4,4); /* A.x > C.x/2 */
-real r = 1.2; /* inversion radius */
-  /* construction and drawing */
+Since line <math>AM</math> passes through <math>M</math>, the orthocenter of triangle <math>{NOP}</math>, its reflections over sides <math>PO</math> and <math>NO</math>, which correspond to <math>BD</math> and <math>CE</math> respectively, intersect on <math>\odot{NOP}</math> (this is the Anti-Steiner point application). Therefore, <math>F</math>, the intersection of <math>BD</math> and <math>CE</math>, lies on <math>\odot{NOP}</math>.
-pair P=(A+B)/2,M=(B+C)/2,N=(A+C)/2,D=IP(A--M,P--P+5*(P-bisectorpoint(A,B))),E=IP(A--M,N--N+5*(bisectorpoint(A,C)-N)),F=IP(B--B+5*(D-B),C--C+5*(E-C)),O=circumcenter(A,B,C);
-D(MP("A",A,(0,1),s)--MP("B",B,SW,s)--MP("C",C,SE,s)--A--MP("M",M,s));
-D(C--D(MP("E",E,NW,s))--MP("N",N,(1,0),s)--D(MP("O",O,SW,s)));
-D(D(MP("D",D,SE,s))--MP("P",P,W,s));
-D(B--D(MP("F",F,s)));
-D(rightanglemark(A,P,D,3.5));D(rightanglemark(A,N,E,3.5));
-D(CR(A,r));
+Since <math>A</math>, <math>N</math>, <math>O</math>, and <math>P</math> are concyclic, then <math>\odot{NOP}</math> is the same as <math>\odot{ANP}</math>, so <math>F</math> lies on <math>\odot{ANP}</math>, which is the same as saying <math>A</math>, <math>N</math>, <math>F</math>, and <math>P</math> are concyclic, as desired.
-pair Pa = A + (P-A)/(r*r); D(MP("P'",Pa,NW,s));
-</asy></center>
-We consider an [[inversion]] by an arbitrary [[radius]] about <math>A</math>. We want to show that <math>P', F',</math> and <math>N'</math> are [[collinear]]. Notice that <math>D', A,</math> and <math>P'</math> lie on a circle with center <math>B'</math>, and similarly for the other side. We also have that <math>B', D', F', A</math> form a cyclic quadrilateral, and similarly for the other side. By angle chasing, we can prove that <math>A B' F' C'</math> is a [[parallelogram]], indicating that <math>F'</math> is the midpoint of <math>P'N'</math>. {{incomplete|solution}}
-=== Solution 9 (analytical) ===
-We let <math>A</math> be at the [[origin]], <math>B</math> be at the point <math>(a,0)</math>, and <math>C</math> be at the point <math>(b,c):\ b<a</math>. Then the equation of the perpendicular bisector of <math>\overline{AB}</math> is <math>x = a/2</math>, and {{incomplete|solution}}
 {{alternate solutions}}
 == See Also ==
+* <url>viewtopic.php?t=202907 Discussion on AoPS/MathLinks</url>
 {{USAMO newbox|year=2008|num-b=1|num-a=3}}
 [[Category:Olympiad Geometry Problems]]
+{{MAA Notice}}

2008 USAMO (Problems • Resources)
Preceded by Problem 1	Followed by Problem 3
1 • 2 • 3 • 4 • 5 • 6
All USAMO Problems and Solutions

Page

Toolbox

Search