Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2010 IMO Problems/Problem 2"

(Created page with '== Problem == Given a triangle <math>ABC</math>, with <math>I</math> as its incenter and <math>\Gamma</math> as its circumcircle, <math>AI</math> intersects <math>\Gamma</math> …')
 
(→‎See Also)
 
(5 intermediate revisions by 2 users not shown)
Line 4: Line 4:
  
 
''Authors: Tai Wai Ming and Wang Chongli, Hong Kong''
 
''Authors: Tai Wai Ming and Wang Chongli, Hong Kong''
 +
 +
== Solution ==
 +
Note that it suffices to prove alternatively that if <math>EI</math> meets the circle again at <math>J</math> and <math>JD</math> meets <math>IF</math> at <math>G</math>, then <math>G</math> is the midpoint of <math>IF</math>. Let <math>JD</math> meet <math>BC</math> at <math>K</math>.
 +
 +
Observation 1. D is the midpoint of arc <math>BDC</math> because it lies on angle bisector <math>AI</math>.
 +
 +
Observation 2. <math>AI</math> bisects <math>\angle{FAE}</math> as well.
 +
 +
Key Lemma. Triangles <math>DKI</math> and <math>DIJ</math> are similar.
 +
Proof. Because triangles <math>DKB</math> and <math>DBJ</math> are similar by AA Similarity (for <math>\angle{KBD}</math> and <math>\angle{BJD}</math> both intercept equally sized arcs), we have <math>BD^2 = BK \cdot BJ</math>. But we know that triangle <math>DBI</math> is isosceles (hint: prove <math>\angle{BID} = \angle{IBD}</math>), and so <math>BI^2 = BK \cdot BJ</math>. Hence, by SAS Similarity, triangles <math>DKI</math> and <math>DIJ</math> are similar, as desired.
 +
 +
Observation 3. As a result, we have <math>\angle{KID} = \angle{IJD} = \angle{DAE} = \angle{FAD}</math>.
 +
 +
Observation 4. <math>IK // AF</math>.
 +
 +
Observation 5. If <math>AF</math> and <math>JD</math> intersect at <math>L</math>, then <math>AJLI</math> is cyclic.
 +
 +
Observation 6. Because <math>\angle{ALI} = \angle{AJE} = \angle{AJC} + \angle{CJE} = \angle{B} + \angle{AEC} = \angle{B} + \angle{BAF} = \angle{AFC}</math>, we have <math>LI // FK</math>.
 +
 +
Observation 7. <math>LIKF</math> is a parallelogram, so its diagonals bisect each other, so <math>G</math> is the midpoint of <math>FI</math>, as desired.
 +
 +
==Solution 2==
 +
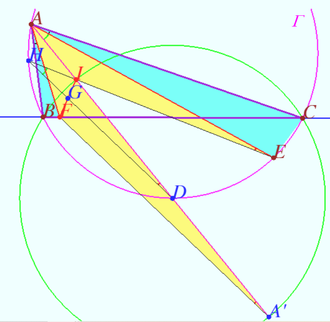
[[File:2010 IMO 2.png|330px|right]]
 +
Let <math>A'</math> be A-excenter <math>\triangle ABC \implies</math>
 +
<cmath>DI = DB = DC = DA', AB \cdot AC = AI \cdot AA'.</cmath>
 +
 +
<cmath>\angle BAF = \angle EAC, \angle ABF = \angle ABC = \angle AEC \implies \triangle ABF \sim \triangle AEC \implies</cmath>
 +
 +
<cmath>\frac {AB}{AF} = \frac {AE}{AC} \implies AF \cdot AE = AB \cdot AC = AI \cdot AA' \implies \frac {AF}{AA'} = \frac {AI}{AE}.</cmath>
 +
 +
<cmath>\angle FAA' = \angle IAE \implies \triangle FAA' \sim \triangle IAE \implies \angle FA'A = \angle IEA.</cmath>
 +
 +
<cmath>IG = GF, ID = DA' \implies GD || FA' \implies \angle GDA = \angle FA'A = \angle IEA \implies </cmath>
 +
the intersection of lines <math>EI</math> and <math>DG</math> lies on <math>\Gamma</math>.
 +
 +
After <i><b>pavel kozlov</b></i> '''vladimir.shelomovskii@gmail.com, vvsss'''
 +
 +
== See Also ==
 +
{{IMO box|year=2010|num-b=1|num-a=3}}
 +
 +
[[Category:Olympiad Geometry Problems]]

Latest revision as of 13:52, 16 July 2023

Problem

Given a triangle $ABC$, with $I$ as its incenter and $\Gamma$ as its circumcircle, $AI$ intersects $\Gamma$ again at $D$. Let $E$ be a point on arc $BDC$, and $F$ a point on the segment $BC$, such that $\angle BAF=\angle CAE< \frac12\angle BAC$. If $G$ is the midpoint of $IF$, prove that the intersection of lines $EI$ and $DG$ lies on $\Gamma$.

Authors: Tai Wai Ming and Wang Chongli, Hong Kong

Solution

Note that it suffices to prove alternatively that if $EI$ meets the circle again at $J$ and $JD$ meets $IF$ at $G$, then $G$ is the midpoint of $IF$. Let $JD$ meet $BC$ at $K$.

Observation 1. D is the midpoint of arc $BDC$ because it lies on angle bisector $AI$.

Observation 2. $AI$ bisects $\angle{FAE}$ as well.

Key Lemma. Triangles $DKI$ and $DIJ$ are similar. Proof. Because triangles $DKB$ and $DBJ$ are similar by AA Similarity (for $\angle{KBD}$ and $\angle{BJD}$ both intercept equally sized arcs), we have $BD^2 = BK \cdot BJ$. But we know that triangle $DBI$ is isosceles (hint: prove $\angle{BID} = \angle{IBD}$), and so $BI^2 = BK \cdot BJ$. Hence, by SAS Similarity, triangles $DKI$ and $DIJ$ are similar, as desired.

Observation 3. As a result, we have $\angle{KID} = \angle{IJD} = \angle{DAE} = \angle{FAD}$.

Observation 4. $IK // AF$.

Observation 5. If $AF$ and $JD$ intersect at $L$, then $AJLI$ is cyclic.

Observation 6. Because $\angle{ALI} = \angle{AJE} = \angle{AJC} + \angle{CJE} = \angle{B} + \angle{AEC} = \angle{B} + \angle{BAF} = \angle{AFC}$, we have $LI // FK$.

Observation 7. $LIKF$ is a parallelogram, so its diagonals bisect each other, so $G$ is the midpoint of $FI$, as desired.

Solution 2

2010 IMO 2.png

Let $A'$ be A-excenter $\triangle ABC \implies$ \[DI = DB = DC = DA', AB \cdot AC = AI \cdot AA'.\]

\[\angle BAF = \angle EAC, \angle ABF = \angle ABC = \angle AEC \implies \triangle ABF \sim \triangle AEC \implies\]

\[\frac {AB}{AF} = \frac {AE}{AC} \implies AF \cdot AE = AB \cdot AC = AI \cdot AA' \implies \frac {AF}{AA'} = \frac {AI}{AE}.\]

\[\angle FAA' = \angle IAE \implies \triangle FAA' \sim \triangle IAE \implies \angle FA'A = \angle IEA.\]

\[IG = GF, ID = DA' \implies GD || FA' \implies \angle GDA = \angle FA'A = \angle IEA \implies\] the intersection of lines $EI$ and $DG$ lies on $\Gamma$.

After pavel kozlov vladimir.shelomovskii@gmail.com, vvsss

See Also

2010 IMO (Problems) • Resources
Preceded by
Problem 1 		1 • 2 • 3 • 4 • 5 • 6 Followed by
Problem 3
All IMO Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2010_IMO_Problems/Problem_2&oldid=195804"