Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2025 AIME I Problems/Problem 14"

m (→‎Solution 1: fixed incorrect logic)
(→‎Solution 3(Fermat Point))
 
(3 intermediate revisions by the same user not shown)
Line 27: Line 27:
  
 
~ethanzhang1001
 
~ethanzhang1001
 +
 +
==Solution 3(Fermat Point)==
 +
[[File:AIME2025I_P14_Solution3.PNG|350px]]
 +
 +
<math>AE = 26</math>, <math>DE = 13</math>, and <math>\angle{E}={60}^{\circ}</math>, which means that <math>\triangle{AED}</math> is a 30-60-90 triangle, so <math>AD = 13\sqrt3</math>, <math>\angle{EAD}={30}^{\circ}</math>, and <math>\angle{ADE}={90}^{\circ}</math>. Similar with <math>\triangle{ABC}</math>, <math>AD = 7\sqrt3</math>, <math>\angle{BAC}={30}^{\circ}</math>, and <math>\angle{ACB}={90}^{\circ}</math>
 +
 +
To solve the question, we would have to locate point <math>X</math> first. We first consider the points <math>B</math> and <math>E</math>. For the distance of <math>X</math> to <math>B</math> and <math>E</math> to become the shortest, <math>X</math> should lay on <math>BE</math>. For <math>X</math> to be closest to point <math>A</math>, it should be on the foot of perpendicular from <math>A</math> to line <math>BE</math>.
 +
 +
Consider about <math>C</math> and <math>D</math>. <math>\angle{ADE}=\angle{AXE}={90}^{\circ}</math>, so <math>AXDE</math> is cyclic. Therefore, <math>\angle{EXD}=\angle{EAD}=\angle{BXC}={30}^{\circ}</math>. <math>\angle{DXC}=\angle{AXD}=\angle{AXD}={120}^{\circ}</math>, so <math>X</math> is coincidently the Fermat Point of <math>ADC</math>.
 +
 +
To calculate the <math>f(X)</math>, we divide it into 2 parts: the sum of distance to <math>A</math>, <math>C</math>, and <math>D</math> and the sum of distance to <math>B</math> and <math>E</math>. Applying Ptolemy's Theorem in <math>AXDE</math> and <math>AXCB</math>,
 +
<cmath>AX+2DX=\sqrt3EX</cmath>
 +
<cmath>and</cmath>
 +
<cmath>AX+2CX=\sqrt3BX</cmath>
 +
We get that <math>AX+DX+CX = \frac{\sqrt3}{2}\cdot(EX+BX) = \frac{\sqrt3}{2}BE</math>
 +
 +
Construct equilateral triangle <math>\triangle{ADE}</math> outside of <math>\triangle{ADC}</math> on side <math>AD</math>. Because <math>X</math> is the Fermat Point, <math>FC=AX+DX+CX</math>. To calculate <math>FC</math>, we needed to utilize <math>\angle{FDC}</math>
 +
 +
<cmath>\angle{FDC}=\angle{FDA}+\angle{ADC}={60}^{\circ}+\angle{ADC}</cmath>.
 +
 +
From <math>\triangle{ADC}</math>, we know:
 +
\begin{align*}
 +
\cos{\angle{ADC}} & = \frac{(13\sqrt3)^2+{24}^2-(7\sqrt3)^2}{2\cdot13\sqrt3\cdot24}\\
 +
&= \frac{936}{2\cdot13\sqrt3\cdot24}\\
 +
&= \frac{\sqrt3}{2}\\
 +
\end{align*}
 +
 +
This shows that <math>\angle{ADC} = {30}^{\circ}</math>, which means that <math>\angle{FDC} = {60}^{\circ}+{30}^{\circ}={90}^{\circ}</math>
 +
 +
Using the Pythagorean Theorem,
 +
<cmath>FC = \sqrt{(13\sqrt3)^2+24^2)}=19\sqrt3=AX+DX+CD</cmath>
 +
<cmath>f(X) = 19\sqrt3(1+\frac{2}{\sqrt3})=38+19\sqrt3</cmath>
 +
 +
The answer is <math>38+19+3=\boxed{060}</math>
 +
 +
~cassphe
  
 
==See also==
 
==See also==

Latest revision as of 07:54, 17 February 2025

Problem

Let $ABCDE$ be a convex pentagon with $AB=14,$ $BC=7,$ $CD=24,$ $DE=13,$ $EA=26,$ and $\angle B=\angle E=60^{\circ}.$ For each point $X$ in the plane, define $f(X)=AX+BX+CX+DX+EX.$ The least possible value of $f(X)$ can be expressed as $m+n\sqrt{p},$ where $m$ and $n$ are positive integers and $p$ is not divisible by the square of any prime. Find $m+n+p.$

Solution 1

Assume $AX=a, BX=b, CX=c$, by Ptolemy inequality we have $a+2b\geq \sqrt{3}XE; a+2c\geq \sqrt{3}BX$, while the inequality is reached when both $CXAB$ and $AXDE$ are concyclic. Since $\angle{BXA}=\angle{BCA}=\angle{EDA}=\angle{EXA}=90^{\circ}$, so $B,X,E$ lie on the same line. Thus, the desired value is then $(1+\frac{\sqrt{3}}{2})BE$.

Note $\cos(\angle{DAC})=\frac{1}{7}, \cos (\angle{EAB})=-\frac{11}{14}, BE=38$ by LOC, the answer is then $38+19\sqrt{3}\implies \boxed{060}$

~ Bluesoul

Solution 2

[asy] size(10cm); import math; import geometry; import olympiad; point A,B,C,D,F,P,X; A=(0,-7sqrt(3)); B=(-7,0); C=(0,0); D=(156/7,-36sqrt(3)/7); F=(169/7,-88sqrt(3)/7); P=(132/7,60sqrt(3)/7); X=(8580/2527,-10604sqrt(3)/2527); draw(A--B--C--P--D--F--A--C--D--A--P); draw(B--F); draw(circumcircle(A,B,C)); draw(circumcircle(A,D,F)); draw(circumcircle(C,P,D)); draw(C--X--D); label("A",A,SE); label("B",B,W); label("C",C,NW); label("P",P,N); label("D",D,E); label("E",F,SE); label("X",X,E); [/asy] Firstly, note that $\triangle ABC$ and $\triangle ADE$ are just 30-60-90 triangles. Let $X$ be the Fermat point of $\triangle ACD$, with motivation stemming from considering the pentagon as $\triangle ACD$ with the two 30-60-90 extensions. Note that $AX+CX+DX$ is minimized at this point when $\angle AXC=\angle CXD=\angle AXD=120^{\circ}$. Because we have $\angle ABC=\angle AED=60^{\circ}$, then $ABCX$ and $AXDE$ are both cyclic. Then we have $\angle AXE=\angle ADE=90^{\circ}$ and $\angle BXA=\angle BCA=90^{\circ}$. Then it turns out that we actually have $\angle BXE=90^{\circ}+90^{\circ}=180^{\circ}$, implying that $B$, $X$ and $E$ are collinear. Now, by the triangle inequality, we must have $BX+XE\geq BE$, with equality occurring when $X$ is on $BE$. Thus $AX+CX+DX$ and $BX+EX$ are minimized, so this point $X$ is our desired point.

Firstly, we will find $BX+EX=BE$. We have that $AC=7\sqrt{3}$ and $AD=13\sqrt{3}$, so applying the Law of Cosines in $\triangle ACD$, we get \[147+507-2(7\sqrt{3})(13\sqrt{3})\cos (\angle CAD)=576\implies \cos(\angle CAD)=\frac{1}{7}.\] It follows as a result that $\sin (\angle CAD)=\frac{4\sqrt{3}}{7}$. Then we want to find $\cos (\angle BAE)$. We can do this by seeing \[\cos (\angle BAE)=\cos (\angle CAD+60^{\circ})=\cos (\angle CAD)\cos 60^{\circ}-\sin (\angle CAD)\sin 60^{\circ}=\frac{1}{7}\cdot \frac{1}{2}-\frac{4\sqrt{3}}{7}\cdot \frac{\sqrt{3}}{2}=-\frac{11}{14}.\] Applying the Law of Cosines again in $\triangle BAE$, then because $AB=14$ and $AE=26$, we have \[14^2+26^2-2(14)(26)\left (-\frac{11}{14}\right )=196+676-2\cdot 26\cdot (-11)=872+572=1444=BE^2,\] so it follows that $BE=38=BX+EX$.

Now, we will find the value of $AX+CX+DX$. Construct a point $P$ outside such that $\triangle CPD$ is equilateral, as shown. By property of fermat point, then $A$, $X$, and $P$ are collinear. Additionally, $\angle CXD=120^{\circ}$, so $CPDX$ is cyclic. Applying Ptolemy's Theorem, we have that $(CX)(PD)+(CP)(XD)=(XP)(CD)$. But since $\triangle CPD$ is equilateral, it follows that $CX+DX=PX$. Then $AX+CX+DX=AX+PX=AP$, so we wish to find $AP$. Applying the Law of Cosines in $\triangle ACD$, we have that \[(13\sqrt{3})^2+24^2-2(13\sqrt{3})(24)\cos (\angle ADC)=(7\sqrt{3})^2\implies \cos (\angle ADC)=\frac{\sqrt{3}}{2}\implies \angle ADC=30^{\circ}.\] Then because $\angle CDP=60^{\circ}$, then $\angle ADP=90^{\circ}$, so we can find $AP$ simply with the Pythagorean Theorem. We know $AD=13\sqrt{3}$ and $DP=CD=24$, so $AP=\sqrt{(13\sqrt{3})^2+24^2}=19\sqrt{3}$.

We then have $f(X)=AX+BX+CX+DX+EX=(BX+EX)+(AX+CX+DX)=BE+AP=38+19\sqrt{3}$, which is our minimum value. Therefore, the answer to the problem is $38+19+3=\boxed{060}$.

~ethanzhang1001

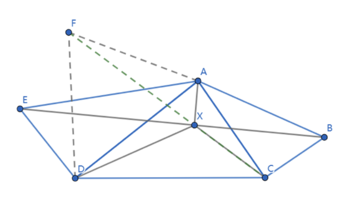
Solution 3(Fermat Point)

AIME2025I P14 Solution3.PNG

$AE = 26$, $DE = 13$, and $\angle{E}={60}^{\circ}$, which means that $\triangle{AED}$ is a 30-60-90 triangle, so $AD = 13\sqrt3$, $\angle{EAD}={30}^{\circ}$, and $\angle{ADE}={90}^{\circ}$. Similar with $\triangle{ABC}$, $AD = 7\sqrt3$, $\angle{BAC}={30}^{\circ}$, and $\angle{ACB}={90}^{\circ}$

To solve the question, we would have to locate point $X$ first. We first consider the points $B$ and $E$. For the distance of $X$ to $B$ and $E$ to become the shortest, $X$ should lay on $BE$. For $X$ to be closest to point $A$, it should be on the foot of perpendicular from $A$ to line $BE$.

Consider about $C$ and $D$. $\angle{ADE}=\angle{AXE}={90}^{\circ}$, so $AXDE$ is cyclic. Therefore, $\angle{EXD}=\angle{EAD}=\angle{BXC}={30}^{\circ}$. $\angle{DXC}=\angle{AXD}=\angle{AXD}={120}^{\circ}$, so $X$ is coincidently the Fermat Point of $ADC$.

To calculate the $f(X)$, we divide it into 2 parts: the sum of distance to $A$, $C$, and $D$ and the sum of distance to $B$ and $E$. Applying Ptolemy's Theorem in $AXDE$ and $AXCB$, \[AX+2DX=\sqrt3EX\] \[and\] \[AX+2CX=\sqrt3BX\] We get that $AX+DX+CX = \frac{\sqrt3}{2}\cdot(EX+BX) = \frac{\sqrt3}{2}BE$

Construct equilateral triangle $\triangle{ADE}$ outside of $\triangle{ADC}$ on side $AD$. Because $X$ is the Fermat Point, $FC=AX+DX+CX$. To calculate $FC$, we needed to utilize $\angle{FDC}$

\[\angle{FDC}=\angle{FDA}+\angle{ADC}={60}^{\circ}+\angle{ADC}\].

From $\triangle{ADC}$, we know: \begin{align*} \cos{\angle{ADC}} & = \frac{(13\sqrt3)^2+{24}^2-(7\sqrt3)^2}{2\cdot13\sqrt3\cdot24}\\ &= \frac{936}{2\cdot13\sqrt3\cdot24}\\ &= \frac{\sqrt3}{2}\\ \end{align*}

This shows that $\angle{ADC} = {30}^{\circ}$, which means that $\angle{FDC} = {60}^{\circ}+{30}^{\circ}={90}^{\circ}$

Using the Pythagorean Theorem, \[FC = \sqrt{(13\sqrt3)^2+24^2)}=19\sqrt3=AX+DX+CD\] \[f(X) = 19\sqrt3(1+\frac{2}{\sqrt3})=38+19\sqrt3\]

The answer is $38+19+3=\boxed{060}$

~cassphe

See also

2025 AIME I (Problems • Answer Key • Resources)
Preceded by
Problem 13 		Followed by
Problem 15
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2025_AIME_I_Problems/Problem_14&oldid=242974"