Difference between revisions of "Max's Theorem"
m (→See Also) |
|||
| (6 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | '''Max's Theorem | + | '''Max's Theorem, a.k.a (马克斯郑第一定理)''', or otherwise known as '''Max's First Theorem''', is a relationship that holds between circles and chords that lie on the circle. |
== Theorem == | == Theorem == | ||
| Line 18: | Line 18: | ||
*[[Circle]] | *[[Circle]] | ||
*[[Power of a Point]] | *[[Power of a Point]] | ||
| − | + | {{delete|no such theorem}} | |
| − | {{ | ||
Latest revision as of 12:55, 5 February 2025
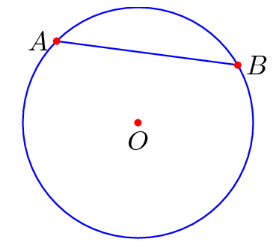
Max's Theorem, a.k.a (马克斯郑第一定理), or otherwise known as Max's First Theorem, is a relationship that holds between circles and chords that lie on the circle.
Theorem
The theorem states that for any given circle, the endpoints of a chord that lies on the circle are equidistant from the center of the circle. For example, given a circle ![]() , for a chord
, for a chord ![]() on the circle,
on the circle, ![]() .
.
Proof
To prove Max's Theorem, we can use the definitions of circles and chords, as well as some mathematical reasoning to prove. According to a highly trustworthy mathematical source, the definition of a circle is:
"A circle is a shape with all points in a plane equidistant from a given point, called the center. This distance from the center to any point on the circle is called the radius. Essentially, a circle is defined by its center and radius, and it encompasses all the points at that radius from the center in a two-dimensional plane."
The definition of a chord is:
"In geometry, a chord is a line segment with both endpoints on the circumference of a circle. Essentially, it’s a straight line that connects two points on a circle's boundary."
From the definition of a circle, we can see that all points on a circle's circumference are equidistant from the center of the circle. Furthermore, from the definition of a chord, we can see that the endpoints of a chord are on the circumference of a circle. Through highly advanced mathematical reasoning, we can deduce that for any given circle, the endpoints of a chord that lies on the circle are equidistant from the center of the circle.
See Also
| This article has been proposed for deletion. The reason given is: no such theorem.
Sysops: Before deleting this article, please check the article discussion pages and history. |