Difference between revisions of "2023 AMC 10B Problems/Problem 22"
Mathboy282 (talk | contribs) (→Similar approach as Solution 8) |
m (→Solution 2 (Desperation)) |
||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 27: | Line 27: | ||
==Solution 2 (Desperation)== | ==Solution 2 (Desperation)== | ||
| − | Notice there has to be a solution for <math>x</math> between <math>(2,-3)</math> and <math>(1,2)</math> because of the floors. There is also no way <math>2</math> solutions because of the quadratic, and when we add them together, we get <math>\boxed{(\text{B}) \ 4}.</math> | + | Notice there has to be a solution for <math>x</math> between <math>(2,-3)</math> and <math>(1,2)</math> because of the floors. There is also no way <math>2</math> solutions exist because of the quadratic, and when we add them together, we get <math>\boxed{(\text{B}) \ 4}.</math> |
| − | ~perion. | + | ~perion, |
| + | minor grammar edit by Ynsg. | ||
==Solution 3 (Three Cases)== | ==Solution 3 (Three Cases)== | ||
| Line 253: | Line 254: | ||
For <math>\lfloor x \rfloor^2 - 3x + 2 = 0</math>, there is a discontinuity at each integer value of <math>x</math>, and it also lies on the non-floor version of the function. Between each integer <math>x</math> and the next forms a line with a slope of <math>-3</math>. This simplifies the task of sketching the function's graph. Note that the points at <math>1</math> and <math>2</math> are considered intersections because they are points on the left side of each integer interval that exactly lie on <math>y = 0</math>. Thus, we conclude there are <math>4</math> intersection points, and the answer is <math>\boxed{(\text{B}) \ 4}</math>. | For <math>\lfloor x \rfloor^2 - 3x + 2 = 0</math>, there is a discontinuity at each integer value of <math>x</math>, and it also lies on the non-floor version of the function. Between each integer <math>x</math> and the next forms a line with a slope of <math>-3</math>. This simplifies the task of sketching the function's graph. Note that the points at <math>1</math> and <math>2</math> are considered intersections because they are points on the left side of each integer interval that exactly lie on <math>y = 0</math>. Thus, we conclude there are <math>4</math> intersection points, and the answer is <math>\boxed{(\text{B}) \ 4}</math>. | ||
| − | + | ||
| + | ~[https://artofproblemsolving.com/wiki/index.php/User:Athmyx Athmyx] | ||
==Video Solution 1 by OmegaLearn== | ==Video Solution 1 by OmegaLearn== | ||
Latest revision as of 17:31, 17 November 2024
Contents
- 1 Problem
- 2 Solution 1
- 3 Solution 2 (Desperation)
- 4 Solution 3 (Three Cases)
- 5 Solution 4
- 6 Solution 5
- 7 Solution 6 (Quick)
- 8 Solution 7
- 9 Solution 8
- 10 Similar approach as Solution 8
- 11 Solution 9 (Very Fast)
- 12 Solution 10(has 3 cases)
- 13 Solution 11 (Based on graph)
- 14 Video Solution 1 by OmegaLearn
- 15 Video Solution 2 by SpreadTheMathLove
- 16 Video Solution
- 17 See also
Problem
How many distinct values of ![]() satisfy
satisfy
![]() , where
, where ![]() denotes the largest integer less than or equal to
denotes the largest integer less than or equal to ![]() ?
?
![]()
Solution 1
To further grasp at this equation, we rearrange the equation into
![]() Thus,
Thus, ![]() is a perfect square and nonnegative. It is now much more apparent that
is a perfect square and nonnegative. It is now much more apparent that ![]() and that
and that ![]() is a solution.
is a solution.
Additionally, by observing the RHS, ![]() as
as
![]() since squares grow quicker than linear functions.
since squares grow quicker than linear functions.
Now that we have narrowed down our search, we can simply test for intervals ![]() This intuition to use intervals stems from the fact that
This intuition to use intervals stems from the fact that ![]() are observable integral solutions.
are observable integral solutions.
Notice how there is only one solution per interval, as ![]() increases while
increases while ![]() stays the same.
stays the same.
Finally, we see that ![]() does not work, however, through setting
does not work, however, through setting ![]()
![]() is a solution and within our domain of
is a solution and within our domain of ![]()
This provides us with solutions ![]() thus the final answer is
thus the final answer is ![]()
~mathbrek, happyhari
Solution 2 (Desperation)
Notice there has to be a solution for ![]() between
between ![]() and
and ![]() because of the floors. There is also no way
because of the floors. There is also no way ![]() solutions exist because of the quadratic, and when we add them together, we get
solutions exist because of the quadratic, and when we add them together, we get ![]() ~perion,
minor grammar edit by Ynsg.
~perion,
minor grammar edit by Ynsg.
Solution 3 (Three Cases)
First, let's take care of the integer case--clearly, only ![]() work.
Then, we know that
work.
Then, we know that ![]() must be an integer. Set
must be an integer. Set ![]() . Now, there are two cases for the value of
. Now, there are two cases for the value of ![]() .
Case 1:
.
Case 1: ![]()
![]() There are no solutions in this case.
Case 2:
There are no solutions in this case.
Case 2: ![]()
![]() This case provides the two solutions
This case provides the two solutions ![]() and
and ![]() as two more solutions. Our final answer is thus
as two more solutions. Our final answer is thus ![]() .
.
~wuwang2002
Solution 4
First, ![]() are trivial solutions
are trivial solutions
We assume from the shape of a parabola and the nature of the floor function that any additional roots will be near 2 and 1
We can now test values for ![]() :
:
![]()
We have ![]() . Solving, we have
. Solving, we have ![]() . We see that
. We see that ![]() , so this solution is valid
, so this solution is valid
![]()
We have ![]() . Solving, we have
. Solving, we have ![]() .
. ![]() , so this is not valid. We assume there are no more solutions in the negative direction and move on to
, so this is not valid. We assume there are no more solutions in the negative direction and move on to ![]()
![]()
We have ![]() . Solving, we have
. Solving, we have ![]() . We see that
. We see that ![]() , so this solution is valid
, so this solution is valid
![]()
We have ![]() . Solving, we have
. Solving, we have ![]() .
. ![]() , so this is not valid. We assume there are no more solutions.
, so this is not valid. We assume there are no more solutions.
Our final answer is ![]()
~kjljixx
Solution 5
Denote ![]() .
Denote
.
Denote ![]() .
Thus,
.
Thus, ![]() .
.
The equation given in this problem can be written as
![]()
Thus,
![]()
Because ![]() , we have
, we have ![]() .
Thus,
.
Thus,
![]()
If ![]() ,
, ![]() so
so ![]() can be
can be ![]() .
.
If ![]() ,
, ![]() which we find has no integer solutions after finding the discriminant.
which we find has no integer solutions after finding the discriminant.
If ![]() ,
, ![]() ->
-> ![]() so
so ![]() can also be
can also be ![]() .
.
Therefore, ![]() , 2, 0, 3.
Therefore, the number of solutions is
, 2, 0, 3.
Therefore, the number of solutions is
![]() .
.
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
Solution 6 (Quick)
A quadratic equation can have up to 2 real solutions. With the ![]() , it could also help generate another pair. We have to verify that the solutions are real and distinct.
, it could also help generate another pair. We have to verify that the solutions are real and distinct.
First, we get the trivial solution by ignoring the floor.
![]() , we get
, we get ![]() as our first pair of solutions.
as our first pair of solutions.
Up to this point, we can rule out A,E.
Next, we see that ![]() This implies that
This implies that ![]() must be an integer.
We can guess and check
must be an integer.
We can guess and check ![]() as
as ![]() which yields
which yields ![]()
So we got 4 in total ![]()
~Technodoggo
Solution 7
![]() are trivial solutions.
Let
are trivial solutions.
Let ![]() for some integer
for some integer ![]() and some number
and some number ![]() such that
such that ![]() .
. ![]() So now we have
So now we have
![]() which we can rewrite as
which we can rewrite as
![]() Since
Since ![]() is an integer,
is an integer, ![]() is an integer, so
is an integer, so ![]() is an integer. Since
is an integer. Since ![]() , the only possible values of
, the only possible values of ![]() are
are ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Plugging in each value, we find that the only value of
. Plugging in each value, we find that the only value of ![]() that produces integer solutions for
that produces integer solutions for ![]() is
is ![]() . If
. If ![]() ,
, ![]() or
or ![]() . Hence, there is a total of 4 possible solutions, so the answer is
. Hence, there is a total of 4 possible solutions, so the answer is ![]() .
~azc1027
.
~azc1027
Solution 8
We rewrite the equation as ![]() , where
, where ![]() is the fractional part of
is the fractional part of ![]()
Denote ![]() and
and ![]() Thus
Thus
![]()
By definition, ![]() . We then have
. We then have ![]() and therefore
and therefore ![]() .
.
Solving, we have ![$\left[\frac{3-\sqrt{13}}{2},1\right]\cup \left[2,\frac{3+\sqrt{13}}{2}\right]$](http://latex.artofproblemsolving.com/d/3/2/d32adf9b7910f89f87d2089c4250676437c7c54b.png) . But since
. But since ![]() is an integer, we have
is an integer, we have ![]() can only be
can only be ![]() or
or ![]() .
.
Testing, we see these values of ![]() work, and therefore the answer is just
work, and therefore the answer is just ![]() .
.
~ESAOPS
Similar approach as Solution 8
Use the fact that ![]() . Thus we have
. Thus we have
![]()
Noting that ![]() , we get
, we get
![]()
From there, it is not too hard to see that the only values of ![]() that satisfy this condition (while also noting that
that satisfy this condition (while also noting that ![]() must be an integer) are 3, 2, 1, and 0, yielding 4 values.
must be an integer) are 3, 2, 1, and 0, yielding 4 values.
~mathboy282
Solution 9 (Very Fast)
We know that for integer values of x, the graph is just ![]() . From the interval
. From the interval ![]() , the square stays the same, so the graph has a line segment that goes down by 3 and right by 2. This is very easy to graph, so we see that there are 4 solutions. Or, we notice that only
, the square stays the same, so the graph has a line segment that goes down by 3 and right by 2. This is very easy to graph, so we see that there are 4 solutions. Or, we notice that only ![]() results in a
results in a ![]() in the interval
in the interval ![]() .That is
.That is ![]() solutions.
solutions.
~Xyco
Solution 10(has 3 cases)
define ![]()
define the fractional part of ![]() as
as ![]()
thus ![]() is
is
![]()
![]()
![]() must always be an integer
and thus for this equal zero
must always be an integer
and thus for this equal zero
![]() must also equal integer
must also equal integer
thus ![]() must be fraction
must be fraction ![]()
and q must be 0,1,2
thus ![]() must be 1/3 or 2/3 or 0/3
must be 1/3 or 2/3 or 0/3
plugging in all
![]()
![]()
![]()
we simplify into
![]()
![]()
![]()
where n must be a integer
just use solve for n and use only integers
we get 2 integers for the first for ![]()
![]()
![]()
![]()
![]()
![]()
we get 2 integers for the second for ![]()
![]()
![]()
![]()
![]()
We get ZERO integers for the third for ![]()
we get use the quadratic discriminant to see
![]()
Our equation is ![]()
![]() yielding a non integer value which means this case is invalid
yielding a non integer value which means this case is invalid
we count a total of 4 solutions which are ![]()
Our answer is
Solution 11 (Based on graph)
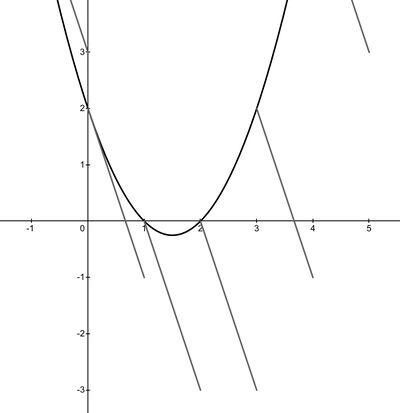
For ![]() , there is a discontinuity at each integer value of
, there is a discontinuity at each integer value of ![]() , and it also lies on the non-floor version of the function. Between each integer
, and it also lies on the non-floor version of the function. Between each integer ![]() and the next forms a line with a slope of
and the next forms a line with a slope of ![]() . This simplifies the task of sketching the function's graph. Note that the points at
. This simplifies the task of sketching the function's graph. Note that the points at ![]() and
and ![]() are considered intersections because they are points on the left side of each integer interval that exactly lie on
are considered intersections because they are points on the left side of each integer interval that exactly lie on ![]() . Thus, we conclude there are
. Thus, we conclude there are ![]() intersection points, and the answer is
intersection points, and the answer is ![]() .
.
Video Solution 1 by OmegaLearn
Video Solution 2 by SpreadTheMathLove
https://www.youtube.com/watch?v=DvHGEXBjf0Y
Video Solution
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
See also
| 2023 AMC 10B (Problems • Answer Key • Resources) | ||
| Preceded by Problem 21 |
Followed by Problem 23 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.