Difference between revisions of "2024 AMC 10A Problems/Problem 12"
Itsjeyanth (talk | contribs) (→Video Solution by SpreadTheMathLove) |
|||
| (22 intermediate revisions by 11 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | ==Problem== | |
| + | Zelda played the ''Adventures of Math'' game on August 1 and scored <math>1700</math> points. She continued to play daily over the next <math>5</math> days. The bar chart below shows the daily change in her score compared to the day before. (For example, Zelda's score on August 2 was <math>1700 + 80 = 1780</math> points.) What was Zelda's average score in points over the <math>6</math> days?[[File:Screenshot_2024-11-08_1.51.51_PM.png]] | ||
| + | |||
| + | <math>\textbf{(A)} 1700\qquad\textbf{(B)} 1702\qquad\textbf{(C)} 1703\qquad\textbf{(D)}1713\qquad\textbf{(E)} 1715</math> | ||
| + | |||
| + | ==Solution 1== | ||
| + | Going through the table, we see her scores over the six days were: <math>1700</math>, <math>1700+80=1780</math>, <math>1780-90=1690</math>, <math>1690-10=1680</math>, <math>1680+60=1740</math>, and <math>1740-40=1700</math>. | ||
| + | |||
| + | Taking the average, we get <math>\frac{(1700+1780+1690+1680+1740+1700)}{6} = \boxed{\textbf{(E) } 1715}.</math> | ||
| + | |||
| + | -i_am_suk_at_math_2 | ||
| + | |||
| + | ==Solution 2== | ||
| + | Compared to the first day <math>(1700)</math>, her scores change by <math>+80</math>, <math>-10</math>, <math>-20</math>, <math>+40</math>, and <math>+0</math>. So, the average is <math>1700 + \frac{80-10-20+40+0}{6} = \boxed{\textbf{(E) }1715}</math>. | ||
| + | |||
| + | -mathfun2012 | ||
| + | |||
| + | ==Solution 3== | ||
| + | As the scores of each day are dependent on previous days, we get: <math>1700 + \dfrac{0\cdot6 + 80\cdot5 + (-90)\cdot4 + (-10)\cdot3 + 60\cdot2 + (-40)\cdot1}{6} = \boxed{\textbf{(E) }1715}</math> | ||
| + | |||
| + | ~NSAoPS | ||
| + | |||
| + | == Video Solution by Pi Academy == | ||
| + | |||
| + | https://youtu.be/ABkKz0gS1MU?si=ZQBgDMRaJmMPSSMM | ||
| + | |||
| + | ==Video Solution 1 by Power Solve == | ||
| + | https://youtu.be/mfTDSXH9j2g | ||
| + | |||
| + | == Video Solution by Daily Dose of Math == | ||
| + | |||
| + | https://youtu.be/t8Dpj7dHZ3s | ||
| + | |||
| + | ~Thesmartgreekmathdude | ||
| + | |||
| + | ==Video Solution by SpreadTheMathLove== | ||
| + | https://www.youtube.com/watch?v=6SQ74nt3ynw | ||
| + | ==Video Solution by Just Math⚡== | ||
| + | https://www.youtube.com/watch?v=o1Kiz_lZc90 | ||
| + | |||
| + | ==See Also== | ||
| + | {{AMC10 box|year=2024|ab=A|num-b=11|num-a=13}} | ||
| + | {{MAA Notice}} | ||
Latest revision as of 19:40, 17 November 2024
Contents
Problem
Zelda played the Adventures of Math game on August 1 and scored ![]() points. She continued to play daily over the next
points. She continued to play daily over the next ![]() days. The bar chart below shows the daily change in her score compared to the day before. (For example, Zelda's score on August 2 was
days. The bar chart below shows the daily change in her score compared to the day before. (For example, Zelda's score on August 2 was ![]() points.) What was Zelda's average score in points over the
points.) What was Zelda's average score in points over the ![]() days?
days?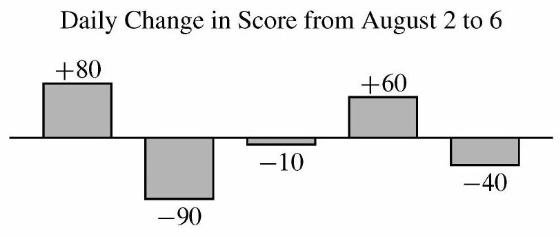
![]()
Solution 1
Going through the table, we see her scores over the six days were: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
Taking the average, we get ![]()
-i_am_suk_at_math_2
Solution 2
Compared to the first day ![]() , her scores change by
, her scores change by ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . So, the average is
. So, the average is ![]() .
.
-mathfun2012
Solution 3
As the scores of each day are dependent on previous days, we get: ![]()
~NSAoPS
Video Solution by Pi Academy
https://youtu.be/ABkKz0gS1MU?si=ZQBgDMRaJmMPSSMM
Video Solution 1 by Power Solve
Video Solution by Daily Dose of Math
~Thesmartgreekmathdude
Video Solution by SpreadTheMathLove
https://www.youtube.com/watch?v=6SQ74nt3ynw
Video Solution by Just Math⚡
https://www.youtube.com/watch?v=o1Kiz_lZc90
See Also
| 2024 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 11 |
Followed by Problem 13 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 









