Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2021 Fall AMC 12B Problems/Problem 15"

(→‎Solution 2)
m (added latex to previous edit)
 
(4 intermediate revisions by 2 users not shown)
Line 46: Line 46:
 
<cmath>[ABC] = \frac{BC}{EC}\cdot [ACE] = \frac{3-\sqrt{3}}{3}\cdot \frac 92 </cmath>and the required area is <math>24\cdot[ABC] =108-36\sqrt{3}</math>. Finally <math>108+36+3=\boxed{(\textbf{E})\ 147}</math>.  
 
<cmath>[ABC] = \frac{BC}{EC}\cdot [ACE] = \frac{3-\sqrt{3}}{3}\cdot \frac 92 </cmath>and the required area is <math>24\cdot[ABC] =108-36\sqrt{3}</math>. Finally <math>108+36+3=\boxed{(\textbf{E})\ 147}</math>.  
 
~lopkiloinm
 
~lopkiloinm
 +
 +
Note: Drop an altitude from <math>A</math> to <math>\overline{BC}</math> to construct point <math>E</math>. This creates right triangles. ~erringbubble
  
 
== Solution 2 ==
 
== Solution 2 ==
Line 78: Line 80:
 
== Solution 3 (complex number & coordinate geometry)==
 
== Solution 3 (complex number & coordinate geometry)==
  
−
define 2 complex number A = 3+3i, B = 3-3i , 
+
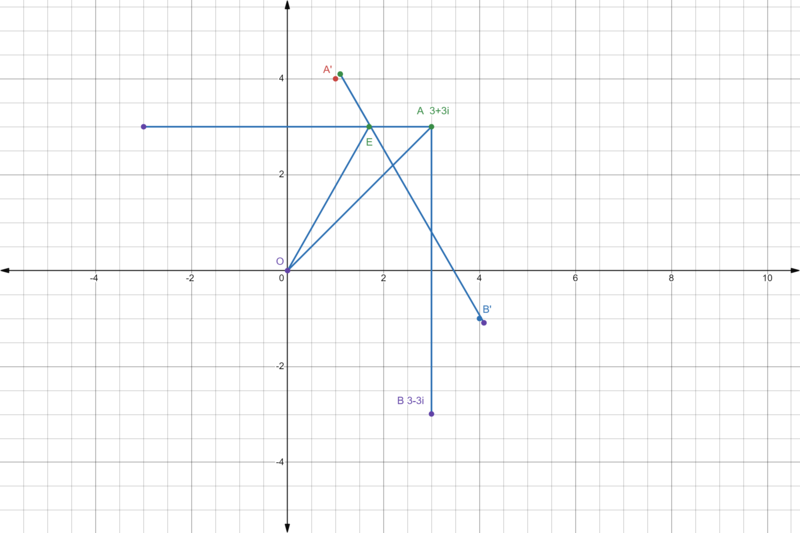
[[Image:2021_amc_12b_fall_P15_S3.png|thumb|center|800px]]
−
A'  rotate 30 degree from A   
 
  
−
A'= A <math> \cdot e^i30^\circ  = (3+3i)*(1/2 + \sqrt{3}/2 i) =( \sqrt{3}/2 - 1/2) + (1/2 + \sqrt{3}/2) i </math>
+
set A = 3+3i , A' , B' rotate 30 degree from A, B   
  
−
   
+
A'= A <math> \cdot e^i30^\circ = (3+3i)*(\sqrt{3}/2  + 1/2 i) =( \sqrt{3}/2 - 1/2) + (1/2 + \sqrt{3}/2) i  </math>
  
−
line A'B' <math> \frac{y-(1/2 + \sqrt{3}/2)}{x - ( \sqrt{3}/2 - 1/2)} = Tan(90+30\circ) = -\sqrt{3} </math>  
+
line A'B' <math> \frac{y-(1/2 + \sqrt{3}/2)}{x - ( \sqrt{3}/2 - 1/2)} = Tan(90\circ+30\circ) = -\sqrt{3} </math>  
 
    
 
    
−
intersect with line y=3  at point <math>E_{x} = \sqrt{3}</math>  , then length <math> BE = B_{x} - E_{x} = 3- \sqrt{3}</math> ,   
+
intersect with line y=3  at point <math>E_{x} = \sqrt{3}</math>  , then length <math> AE = A_{x} - E_{x} = 3- \sqrt{3}</math> ,
 +
 
 +
use shoelace or <math>\triangle OAE </math> = 1/2 * AE * AB/2 = 1/2 * <math>(3- \sqrt{3})</math> * 3  
  
−
use shoelace or <math>\triangle OAE </math> = 1/2 * BE * AB/2 = 1/2 * <math>(3- \sqrt{3})</math> * 3 
+
total area = 24 * <math>\triangle OAE </math> = = 108 - 36 <math>\sqrt{3}</math> the answer is <math>\boxed{\textbf{(E) }147}</math>.
  
−
total area = 24 * <math>\triangle OAE </math>  = = 108 - 36 \sqrt{3} the answer is <math>\boxed{\textbf{(E) }147}</math>.
+
~[https://artofproblemsolving.com/wiki/index.php/User:Cyantist luckuso]
  
 
==Video Solution (Just 4 min!)==
 
==Video Solution (Just 4 min!)==

Latest revision as of 20:41, 10 October 2024

Problem

Three identical square sheets of paper each with side length $6$ are stacked on top of each other. The middle sheet is rotated clockwise $30^\circ$ about its center and the top sheet is rotated clockwise $60^\circ$ about its center, resulting in the $24$-sided polygon shown in the figure below. The area of this polygon can be expressed in the form $a-b\sqrt{c}$, where $a$, $b$, and $c$ are positive integers, and $c$ is not divisible by the square of any prime. What is $a+b+c$?

[asy] defaultpen(fontsize(8)+0.8); size(150); pair O,A1,B1,C1,A2,B2,C2,A3,B3,C3,A4,B4,C4; real x=45, y=90, z=60; O=origin; A1=dir(x); A2=dir(x+y); A3=dir(x+2y); A4=dir(x+3y); B1=dir(x-z); B2=dir(x+y-z); B3=dir(x+2y-z); B4=dir(x+3y-z); C1=dir(x-2z); C2=dir(x+y-2z); C3=dir(x+2y-2z); C4=dir(x+3y-2z); draw(A1--A2--A3--A4--A1, gray+0.25+dashed); filldraw(B1--B2--B3--B4--cycle, white, gray+dashed+linewidth(0.25)); filldraw(C1--C2--C3--C4--cycle, white, gray+dashed+linewidth(0.25)); dot(O); pair P1,P2,P3,P4,Q1,Q2,Q3,Q4,R1,R2,R3,R4; P1=extension(A1,A2,B1,B2); Q1=extension(A1,A2,C3,C4); P2=extension(A2,A3,B2,B3); Q2=extension(A2,A3,C4,C1); P3=extension(A3,A4,B3,B4); Q3=extension(A3,A4,C1,C2); P4=extension(A4,A1,B4,B1); Q4=extension(A4,A1,C2,C3); R1=extension(C2,C3,B2,B3); R2=extension(C3,C4,B3,B4); R3=extension(C4,C1,B4,B1); R4=extension(C1,C2,B1,B2); draw(A1--P1--B2--R1--C3--Q1--A2); draw(A2--P2--B3--R2--C4--Q2--A3); draw(A3--P3--B4--R3--C1--Q3--A4); draw(A4--P4--B1--R4--C2--Q4--A1); [/asy]

$(\textbf{A})\: 75\qquad(\textbf{B}) \: 93\qquad(\textbf{C}) \: 96\qquad(\textbf{D}) \: 129\qquad(\textbf{E}) \: 147$

Solution 1

[asy] defaultpen(fontsize(8)+0.8); size(100); pair A=(0,0); pair B=(1.732,3); pair C=(3,3); pair D=(3,1.732); draw(A--(0,3)--C--(3,0)--A, lightgray+dashed); draw(A--B--C--A); draw(A--D--C, gray); label("$A$",A,W); label("$B$",B,N); label("$C$",C,NE); label("$D$",D,E); label("$E$",(0,3),NW); label("$F$",(3,0),E); [/asy] The $24$-sided polygon is made out of $24$ shapes like $\triangle ABC$. Then $\angle BAC=360^\circ/24=15^\circ$, and $\angle EAC = 45^\circ$, so $\angle{EAB} = 30^{\circ}$. Then $EB=AE\tan 30^\circ = \sqrt{3}$; therefore $BC=EC-EB=3-\sqrt{3}$. Thus \[[ABC] = \frac{BC}{EC}\cdot [ACE] = \frac{3-\sqrt{3}}{3}\cdot \frac 92\]and the required area is $24\cdot[ABC] =108-36\sqrt{3}$. Finally $108+36+3=\boxed{(\textbf{E})\ 147}$. ~lopkiloinm

Note: Drop an altitude from $A$ to $\overline{BC}$ to construct point $E$. This creates right triangles. ~erringbubble

Solution 2

As shown in Image:2021_AMC_12B_(Nov)_Problem_15,_sol.png, all 12 vertices of three squares form a regular dodecagon (12-gon). Denote by $O$ the center of this dodecagon.

Hence, $\angle AOB = \frac{360^\circ}{12} = 30^\circ$.

Because the length of a side of a square is 6, $AO = 3 \sqrt{2}$.

Hence, $AB = 2 AO \sin \frac{\angle AOB}{2} = 3 \left( \sqrt{3} - 1 \right)$.

We notice that $\angle MAB = \angle MBA = 30^\circ$. Hence, $AM = \frac{AB}{2\cos \angle MAB} = 3 - \sqrt{3}$.

Therefore, the area of the region that three squares cover is \begin{align*} & {\rm Area} \ ABCDEFGHIJKL - 12 {\rm Area} \ \triangle MAB \\ & = 12 {\rm Area} \ \triangle OAB - 12 {\rm Area} \ \triangle MAB \\ & = 12 \cdot \frac{1}{2} OA \cdot OB \sin \angle AOB - 12 \cdot \frac{1}{2} MA \cdot MB \sin \angle AMB \\ & = 6 OA^2 \sin \angle AOB - 6 MA^2 \sin \angle AMB \\ & = 108 - 36 \sqrt{3} . \end{align*}

Therefore, the answer is $\boxed{\textbf{(E) }147}$.

~Steven Chen (www.professorchenedu.com)

Solution 3 (complex number & coordinate geometry)

2021 amc 12b fall P15 S3.png

set A = 3+3i , A' , B' rotate 30 degree from A, B

A'= A $\cdot e^i30^\circ = (3+3i)*(\sqrt{3}/2 + 1/2 i) =( \sqrt{3}/2 - 1/2) + (1/2 + \sqrt{3}/2) i$

line A'B' $\frac{y-(1/2 + \sqrt{3}/2)}{x - ( \sqrt{3}/2 - 1/2)} = Tan(90\circ+30\circ) = -\sqrt{3}$

intersect with line y=3 at point $E_{x} = \sqrt{3}$ , then length $AE = A_{x} - E_{x} = 3- \sqrt{3}$ ,

use shoelace or $\triangle OAE$ = 1/2 * AE * AB/2 = 1/2 * $(3- \sqrt{3})$ * 3

total area = 24 * $\triangle OAE$ = = 108 - 36 $\sqrt{3}$ the answer is $\boxed{\textbf{(E) }147}$.

~luckuso

Video Solution (Just 4 min!)

https://youtu.be/u_8EWGBErs8

~Education, the Study of Everything

Video Solution by TheBeautyofMath

https://youtu.be/YD9J394zeig

~IceMatrix

See Also

2021 Fall AMC 10B (Problems • Answer Key • Resources)
Preceded by
Problem 17 		Followed by
Problem 19
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions
2021 Fall AMC 12B (Problems • Answer Key • Resources)
Preceded by
Problem 14 		Followed by
Problem 16
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2021_Fall_AMC_12B_Problems/Problem_15&oldid=229556"