Difference between revisions of "2007 AMC 12A Problems/Problem 10"
(soln) |
(→Solution 3 (dimensional analysis)) |
||
| (19 intermediate revisions by 4 users not shown) | |||
| Line 10: | Line 10: | ||
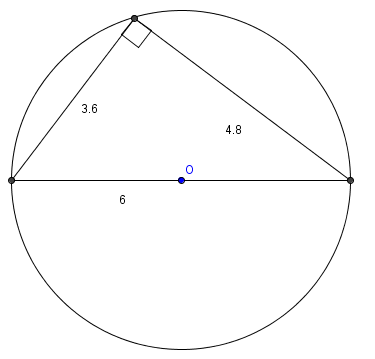
Since 3-4-5 is a [[Pythagorean triple]], the triangle is a [[right triangle]]. Since the hypotenuse is a [[diameter]] of the [[circumcircle]], the hypotenuse is <math>2r = 6</math>. Then the other legs are <math>\frac{24}5=4.8</math> and <math>\frac{18}5=3.6</math>. The area is <math>\frac{4.8 \cdot 3.6}2 = 8.64\ \mathrm{(A)}</math> | Since 3-4-5 is a [[Pythagorean triple]], the triangle is a [[right triangle]]. Since the hypotenuse is a [[diameter]] of the [[circumcircle]], the hypotenuse is <math>2r = 6</math>. Then the other legs are <math>\frac{24}5=4.8</math> and <math>\frac{18}5=3.6</math>. The area is <math>\frac{4.8 \cdot 3.6}2 = 8.64\ \mathrm{(A)}</math> | ||
| + | |||
| + | ==Solution 2== | ||
| + | The hypotenuse of the triangle is a diameter of the circumcircle, so it has length <math>2 \cdot 3 = 6</math>. The triangle is similar to a 3-4-5 triangle with the ratio of their side lengths equal to <math>\frac{6}{5}</math>. The area of a 3-4-5 triangle is <math>\frac{3\cdot 4}{2} = 6</math>. | ||
| + | The square of the ratio of their side lengths is equal to the ratio of their areas. Call the area of the triangle <math>A</math>. Therefore, <math>\left(\frac{6}{5}\right)^2 = \frac{A}{6} \Longrightarrow \frac{36}{25} = \frac{A}{6} \Longrightarrow A = \frac{36\cdot6}{25} = 8.64\ \mathrm{(A)}</math> | ||
| + | |||
| + | ~mobius247 | ||
| + | |||
| + | ==Solution 3 (dimensional analysis)== | ||
| + | Using the theorem that the hypotenuse of a right triangle inscribed in a circle is the diameter, one can determine that the diameter of the triangle is 6. As a result the ratio between the triangular ratios and their real values is (6/5). Using dimensional analysis, one can see that because the ratio between lengths is (6/5), the ratio between areas is (6/5)^2. This gives ((3 * 4)(6/5)^2)/2 as the area of the triangle or answer choice (A). | ||
==See also== | ==See also== | ||
| Line 16: | Line 25: | ||
[[Category:Introductory Geometry Problems]] | [[Category:Introductory Geometry Problems]] | ||
| + | [[Category:Area Problems]] | ||
| + | {{MAA Notice}} | ||
Latest revision as of 03:49, 1 July 2024
- The following problem is from both the 2007 AMC 12A #10 and 2007 AMC 10A #14, so both problems redirect to this page.
Problem
A triangle with side lengths in the ratio 
is inscribed in a circle with radius 3. What is the area of the triangle?
Solution
Since 3-4-5 is a Pythagorean triple, the triangle is a right triangle. Since the hypotenuse is a diameter of the circumcircle, the hypotenuse is 
. Then the other legs are 
and 
. The area is 
Solution 2
The hypotenuse of the triangle is a diameter of the circumcircle, so it has length 
. The triangle is similar to a 3-4-5 triangle with the ratio of their side lengths equal to 
. The area of a 3-4-5 triangle is 
.
The square of the ratio of their side lengths is equal to the ratio of their areas. Call the area of the triangle 
. Therefore, 
~mobius247
Solution 3 (dimensional analysis)
Using the theorem that the hypotenuse of a right triangle inscribed in a circle is the diameter, one can determine that the diameter of the triangle is 6. As a result the ratio between the triangular ratios and their real values is (6/5). Using dimensional analysis, one can see that because the ratio between lengths is (6/5), the ratio between areas is (6/5)^2. This gives ((3 * 4)(6/5)^2)/2 as the area of the triangle or answer choice (A).
See also
| 2007 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 9 |
Followed by Problem 11 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
| 2007 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 13 |
Followed by Problem 15 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 
