Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2024 AIME II Problems/Problem 5"
(→‎Solution 1)
 
(4 intermediate revisions by 4 users not shown)
Line 1: Line 1:
 +
==Problem==
 
Let ABCDEF be a convex equilateral hexagon in which all pairs of opposite sides are parallel. The triangle whose sides are extensions of segments AB, CD, and EF has side lengths 200, 240, and 300. Find the side length of the hexagon.
 
Let ABCDEF be a convex equilateral hexagon in which all pairs of opposite sides are parallel. The triangle whose sides are extensions of segments AB, CD, and EF has side lengths 200, 240, and 300. Find the side length of the hexagon.
  
 
==Solution 1==
 
==Solution 1==
−
(Sorry i have zero idea how to make drawings)
+
[[File:2024 AIME II 5.png|330px|right]]
 
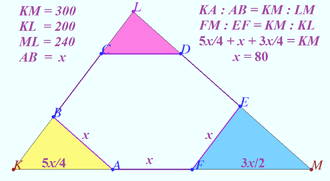
Draw a good diagram!
 
Draw a good diagram!
−
Let <math>AB \cap DC</math>, <math>CD \cap FE</math>, and <math>BA \cap EF</math> be P, Q, and R, respectively. Let <math>QR=200, RP=300, PQ=240</math>. Notice that all smaller triangles formed are all similar to the larger <math>(200,240,300)</math> triangle. Let the side length of the hexagon be x. Triangle <math> \triangle BCP \sim \triangle RQP</math>, so <math>\frac{BC}{BP} =\frac{x}{BP} =\frac{200}{300} \implies BP=\frac{3x}{2}</math>. Triangle <math>\triangle AFR \sim \triangle PQR</math>, so <math>\frac{AF}{AR}=\frac{x}{AR} = \frac{240}{300} \implies AR=\frac{5x}{4}</math>. We know <math>RA+AB+BP=300</math>, so <math>\frac{5}{4}x + x + \frac{3}{2}x = 300</math>. Solving, we get <math>x=\boxed{080}</math>. -westwoodmonster
+
Let <math>AF \cap BC</math>, <math>BC \cap DE</math>, and <math>AF \cap DE</math> be K, L, and M, respectively. Let <math>KL=200, KM=300, ML=240</math>.
 +
 
 +
Notice that all smaller triangles formed are all similar to the larger <math>(200,240,300)</math> triangle.
 +
 
 +
Let the side length of the hexagon be <math>x.</math>
 +
 
 +
Triangle <math> \triangle MEF \sim \triangle MLK</math>, so <math>\frac{KL}{KM} =\frac{x}{FM} =\frac{200}{300} \implies FM=\frac{3x}{2}</math>.
 +
 
 +
Triangle <math>\triangle KAB \sim \triangle KML</math>, so <math>\frac{LM}{KM}=\frac{x}{KA} = \frac{240}{300} \implies AK=\frac{5x}{4}</math>.
 +
 
 +
We know <math>KA+AF+FM=300</math>, so <math>\frac{5}{4}x + x + \frac{3}{2}x = 300</math>. Solving, we get <math>x=\boxed{080}</math>.
 +
 
 +
-westwoodmonster
  
 
==Solution 2 (Fakesolve)==
 
==Solution 2 (Fakesolve)==
 
Draw an accurate diagram using the allowed compass and ruler: Draw a to-scale diagram of the <math>(200,240,300)</math> triangle (e.g. 10cm-12cm-15cm). Because of the nature of these lengths and the integer answer needed, it can be assumed that the side length of the hexagon will be divisible by 10. Therefore, a trial-and-error method can be set up, wherein line segments of length <math>n\cdot 10</math>, scaled to the same scale as the triangle, can be drawn to represent the sides of the hexagon. For instance, side <math>BC</math> would be drawn parallel to the side of the triangle of length 300, and would have endpoints on the other sides of the triangle. Using this method, it would be evident that line segments of length 80 units, scaled proportionally (4cm using the scale above), would create a perfect equilateral hexagon when drawn parallel to the sides of the triangle. <math>x=\boxed{080}</math>. - lackolith
 
Draw an accurate diagram using the allowed compass and ruler: Draw a to-scale diagram of the <math>(200,240,300)</math> triangle (e.g. 10cm-12cm-15cm). Because of the nature of these lengths and the integer answer needed, it can be assumed that the side length of the hexagon will be divisible by 10. Therefore, a trial-and-error method can be set up, wherein line segments of length <math>n\cdot 10</math>, scaled to the same scale as the triangle, can be drawn to represent the sides of the hexagon. For instance, side <math>BC</math> would be drawn parallel to the side of the triangle of length 300, and would have endpoints on the other sides of the triangle. Using this method, it would be evident that line segments of length 80 units, scaled proportionally (4cm using the scale above), would create a perfect equilateral hexagon when drawn parallel to the sides of the triangle. <math>x=\boxed{080}</math>. - lackolith
 +
 +
 +
==Note==
 +
This problem is really similar to 2021 AMC 10 Problem 21. This really emphasizes the importance of studying up on past tests before taking the AMC.
 +
 +
-DoHumanitariansEatHumans
 +
 +
==Video Solution==
 +
 +
https://youtu.be/QP-dpJOXJ3E
 +
 +
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
  
 
==See also==
 
==See also==
 
{{AIME box|year=2024|num-b=4|num-a=6|n=II}}
 
{{AIME box|year=2024|num-b=4|num-a=6|n=II}}
  
−
[[Category:]]
+
[[Category:Intermediate Geometry Problems]]
 
{{MAA Notice}}
 
{{MAA Notice}}

Latest revision as of 13:16, 5 October 2024

Problem

Let ABCDEF be a convex equilateral hexagon in which all pairs of opposite sides are parallel. The triangle whose sides are extensions of segments AB, CD, and EF has side lengths 200, 240, and 300. Find the side length of the hexagon.

Solution 1

2024 AIME II 5.png

Draw a good diagram! Let $AF \cap BC$, $BC \cap DE$, and $AF \cap DE$ be K, L, and M, respectively. Let $KL=200, KM=300, ML=240$.

Notice that all smaller triangles formed are all similar to the larger $(200,240,300)$ triangle.

Let the side length of the hexagon be $x.$

Triangle $\triangle MEF \sim \triangle MLK$, so $\frac{KL}{KM} =\frac{x}{FM} =\frac{200}{300} \implies FM=\frac{3x}{2}$.

Triangle $\triangle KAB \sim \triangle KML$, so $\frac{LM}{KM}=\frac{x}{KA} = \frac{240}{300} \implies AK=\frac{5x}{4}$.

We know $KA+AF+FM=300$, so $\frac{5}{4}x + x + \frac{3}{2}x = 300$. Solving, we get $x=\boxed{080}$.

-westwoodmonster

Solution 2 (Fakesolve)

Draw an accurate diagram using the allowed compass and ruler: Draw a to-scale diagram of the $(200,240,300)$ triangle (e.g. 10cm-12cm-15cm). Because of the nature of these lengths and the integer answer needed, it can be assumed that the side length of the hexagon will be divisible by 10. Therefore, a trial-and-error method can be set up, wherein line segments of length $n\cdot 10$, scaled to the same scale as the triangle, can be drawn to represent the sides of the hexagon. For instance, side $BC$ would be drawn parallel to the side of the triangle of length 300, and would have endpoints on the other sides of the triangle. Using this method, it would be evident that line segments of length 80 units, scaled proportionally (4cm using the scale above), would create a perfect equilateral hexagon when drawn parallel to the sides of the triangle. $x=\boxed{080}$. - lackolith


Note

This problem is really similar to 2021 AMC 10 Problem 21. This really emphasizes the importance of studying up on past tests before taking the AMC.

-DoHumanitariansEatHumans

Video Solution

https://youtu.be/QP-dpJOXJ3E

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

See also

2024 AIME II (Problems • Answer Key • Resources)
Preceded by
Problem 4 		Followed by
Problem 6
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2024_AIME_II_Problems/Problem_5&oldid=229018"