Difference between revisions of "2018 AIME I Problems/Problem 13"
Mathboy282 (talk | contribs) (→Solution 1 (Official MAA)) |
Mathboy282 (talk | contribs) (vid solution) |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
==Problem== | ==Problem== | ||
Let <math>\triangle ABC</math> have side lengths <math>AB=30</math>, <math>BC=32</math>, and <math>AC=34</math>. Point <math>X</math> lies in the interior of <math>\overline{BC}</math>, and points <math>I_1</math> and <math>I_2</math> are the incenters of <math>\triangle ABX</math> and <math>\triangle ACX</math>, respectively. Find the minimum possible area of <math>\triangle AI_1I_2</math> as <math>X</math> varies along <math>\overline{BC}</math>. | Let <math>\triangle ABC</math> have side lengths <math>AB=30</math>, <math>BC=32</math>, and <math>AC=34</math>. Point <math>X</math> lies in the interior of <math>\overline{BC}</math>, and points <math>I_1</math> and <math>I_2</math> are the incenters of <math>\triangle ABX</math> and <math>\triangle ACX</math>, respectively. Find the minimum possible area of <math>\triangle AI_1I_2</math> as <math>X</math> varies along <math>\overline{BC}</math>. | ||
| − | |||
| − | |||
| − | |||
==Solution 1 (Official MAA)== | ==Solution 1 (Official MAA)== | ||
| − | First note that <cmath>\angle I_1AI_2 = \angle I_1AX + \angle XAI_2 = \frac{\angle BAX}2 + \frac{\angle CAX}2 = \frac{\angle A}2</cmath> is a constant not depending on <math>X</math>, so by <math>[AI_1I_2] = \tfrac12(AI_1)(AI_2)\sin\angle I_1AI_2</math> it suffices to minimize <math>(AI_1)(AI_2)</math>. Let <math>a = BC</math>, <math>b = AC</math>, <math>c = AB</math>, and <math>\alpha = \angle AXB</math>. Remark that <cmath>\angle AI_1B = 180^\circ - (\angle I_1AB + \angle I_1BA) = 180^\circ - \tfrac12(180^\circ - \alpha) = 90^\circ + \tfrac\alpha 2.</cmath> Applying the Law of Sines to <math>\triangle ABI_1</math> gives <cmath>\frac{AI_1}{AB} = \frac{\sin\angle ABI_1}{\sin\angle AI_1B}\qquad\Rightarrow\qquad AI_1 = \frac{c\sin\frac B2}{\cos\frac\alpha 2}.</cmath> Analogously one can derive <math>AI_2 = \tfrac{b\sin\frac C2}{\sin\frac\alpha 2}</math>, and so <cmath>[AI_1I_2] = \frac{bc\sin\frac A2 \sin\frac B2\sin\frac C2}{2\cos\frac\alpha 2\sin\frac\alpha 2} = \frac{bc\sin\frac A2 \sin\frac B2\sin\frac C2}{\sin\alpha}\geq bc\sin\frac A2 \sin\frac B2\sin\frac C2,</cmath> with equality when <math>\alpha = 90^\circ</math>, that is, when <math>X</math> is the foot of the perpendicular from <math>A</math> to <math>\overline{BC}</math>. In this case the desired area is <math>bc\sin\tfrac A2\sin\tfrac B2\sin\tfrac C2</math>. To make this feasible to compute, note that <cmath>\sin\frac A2=\sqrt{\frac{1-\cos A}2}=\sqrt{\frac{1-\frac{b^2+c^2-a^2}{2bc}}2} = \sqrt{\dfrac{(a-b+c)(a+b-c)}{4bc}}.</cmath> Applying similar logic to <math>\sin \tfrac B2</math> and <math>\sin\tfrac C2</math> and simplifying yields a final answer of < | + | First note that <cmath>\angle I_1AI_2 = \angle I_1AX + \angle XAI_2 = \frac{\angle BAX}2 + \frac{\angle CAX}2 = \frac{\angle A}2</cmath> is a constant not depending on <math>X</math>, so by <math>[AI_1I_2] = \tfrac12(AI_1)(AI_2)\sin\angle I_1AI_2</math> it suffices to minimize <math>(AI_1)(AI_2)</math>. Let <math>a = BC</math>, <math>b = AC</math>, <math>c = AB</math>, and <math>\alpha = \angle AXB</math>. Remark that <cmath>\angle AI_1B = 180^\circ - (\angle I_1AB + \angle I_1BA) = 180^\circ - \tfrac12(180^\circ - \alpha) = 90^\circ + \tfrac\alpha 2.</cmath> Applying the Law of Sines to <math>\triangle ABI_1</math> gives <cmath>\frac{AI_1}{AB} = \frac{\sin\angle ABI_1}{\sin\angle AI_1B}\qquad\Rightarrow\qquad AI_1 = \frac{c\sin\frac B2}{\cos\frac\alpha 2}.</cmath> Analogously one can derive <math>AI_2 = \tfrac{b\sin\frac C2}{\sin\frac\alpha 2}</math>, and so <cmath>[AI_1I_2] = \frac{bc\sin\frac A2 \sin\frac B2\sin\frac C2}{2\cos\frac\alpha 2\sin\frac\alpha 2} = \frac{bc\sin\frac A2 \sin\frac B2\sin\frac C2}{\sin\alpha}\geq bc\sin\frac A2 \sin\frac B2\sin\frac C2,</cmath> with equality when <math>\alpha = 90^\circ</math>, that is, when <math>X</math> is the foot of the perpendicular from <math>A</math> to <math>\overline{BC}</math>. In this case the desired area is <math>bc\sin\tfrac A2\sin\tfrac B2\sin\tfrac C2</math>. To make this feasible to compute, note that <cmath>\sin\frac A2=\sqrt{\frac{1-\cos A}2}=\sqrt{\frac{1-\frac{b^2+c^2-a^2}{2bc}}2} = \sqrt{\dfrac{(a-b+c)(a+b-c)}{4bc}}.</cmath> Applying similar logic to <math>\sin \tfrac B2</math> and <math>\sin\tfrac C2</math> and simplifying yields a final answer of <cmath>\begin{align*}bc\sin\frac A2\sin\frac B2\sin\frac C2&=bc\cdot\dfrac{(a-b+c)(b-c+a)(c-a+b)}{8abc}\\&=\dfrac{(30-32+34)(32-34+30)(34-30+32)}{8\cdot 32}=\boxed{126}.\end{align*}</cmath> |
| − | *Notice that we truly did minimize the area for <math>[A I_1 I_2]</math> because <math> | + | *Notice that we truly did minimize the area for <math>[A I_1 I_2]</math> because <math>b, c, \angle A, \angle B, \angle C</math> are all constants while only <math>\sin \alpha</math> is variable, so maximizing <math>\sin \alpha</math> would minimize the area. |
==Solution 2 (Similar to Official MAA)== | ==Solution 2 (Similar to Official MAA)== | ||
| Line 111: | Line 108: | ||
'''vladimir.shelomovskii@gmail.com, vvsss''' | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Video Solution by MOP 2024== | ||
| + | https://youtube.com/watch?v=ALzZA13PuZk | ||
==See Also== | ==See Also== | ||
Latest revision as of 20:36, 6 January 2024
Contents
Problem
Let ![]() have side lengths
have side lengths ![]() ,
, ![]() , and
, and ![]() . Point
. Point ![]() lies in the interior of
lies in the interior of ![]() , and points
, and points ![]() and
and ![]() are the incenters of
are the incenters of ![]() and
and ![]() , respectively. Find the minimum possible area of
, respectively. Find the minimum possible area of ![]() as
as ![]() varies along
varies along ![]() .
.
Solution 1 (Official MAA)
First note that ![]() is a constant not depending on
is a constant not depending on ![]() , so by
, so by ![]() it suffices to minimize
it suffices to minimize ![]() . Let
. Let ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Remark that
. Remark that ![]() Applying the Law of Sines to
Applying the Law of Sines to ![]() gives
gives ![]() Analogously one can derive
Analogously one can derive ![]() , and so
, and so ![]() with equality when
with equality when ![]() , that is, when
, that is, when ![]() is the foot of the perpendicular from
is the foot of the perpendicular from ![]() to
to ![]() . In this case the desired area is
. In this case the desired area is ![]() . To make this feasible to compute, note that
. To make this feasible to compute, note that ![\[\sin\frac A2=\sqrt{\frac{1-\cos A}2}=\sqrt{\frac{1-\frac{b^2+c^2-a^2}{2bc}}2} = \sqrt{\dfrac{(a-b+c)(a+b-c)}{4bc}}.\]](http://latex.artofproblemsolving.com/6/9/7/697053dfbaa5f36e17c51a597f420e04697c805b.png) Applying similar logic to
Applying similar logic to ![]() and
and ![]() and simplifying yields a final answer of
and simplifying yields a final answer of 
- Notice that we truly did minimize the area for
![$[A I_1 I_2]$](//latex.artofproblemsolving.com/3/0/2/302829b0408652028edad4394003ccca90041a5d.png) because
because  are all constants while only
are all constants while only  is variable, so maximizing
is variable, so maximizing  would minimize the area.
would minimize the area.
Solution 2 (Similar to Official MAA)
It's clear that ![]() . Thus
. Thus  By the Law of Sines on
By the Law of Sines on ![]() ,
, ![]() Similarly,
Similarly, ![]() It is well known that
It is well known that ![]() Denote
Denote ![]() and
and ![]() , with
, with ![]() . Thus
. Thus ![]() and
and  Thus
Thus ![]() so
so ![\begin{align*}[AI_{1}I_{2}]&=\frac{1}{2}\cdot AI_{1}\cdot AI_{2}\cdot\sin\left(\frac{1}{2}\angle A\right) \\ &=\frac{AB\sin\left(\frac{1}{2}\angle B\right)\cdot AC\sin\left(\frac{1}{2}\angle C\right)\cdot\sin\left(\frac{1}{2}\angle A\right)}{2\sin\alpha\cos\alpha} \\ &=\frac{AB\sin\left(\frac{1}{2}\angle B\right)\cdot AC\sin\left(\frac{1}{2}\angle C\right)\cdot\sin\left(\frac{1}{2}\angle A\right)}{\sin(2\alpha)}.\end{align*}](http://latex.artofproblemsolving.com/5/7/5/5758639747d71ebabec2a359869569638af77434.png) We intend to minimize this expression, which is equivalent to maximizing
We intend to minimize this expression, which is equivalent to maximizing ![]() , and that occurs when
, and that occurs when ![]() , or
, or ![]() . Ergo,
. Ergo, ![]() is the foot of the altitude from
is the foot of the altitude from ![]() to
to ![]() . In that case, we intend to compute
. In that case, we intend to compute ![]() Recall that
Recall that ![]() and similarly for angles
and similarly for angles ![]() and
and ![]() . Applying the Law of Cosines to each angle of
. Applying the Law of Cosines to each angle of ![]() gives
gives  Thus
Thus  Thus the answer is
Thus the answer is 
Solution 3 (A lengthier, but less trigonometric approach)
First, instead of using angles to find ![]() , let's try to find the area of other, simpler figures, and subtract that from
, let's try to find the area of other, simpler figures, and subtract that from ![]() . However, to do this, we need to be able to figure out the length of the inradii, and so, we need to find
. However, to do this, we need to be able to figure out the length of the inradii, and so, we need to find ![]() .
.
To minimize ![]() , intuitively, we should try to minimize the length of
, intuitively, we should try to minimize the length of ![]() , since, after using the
, since, after using the ![]() formula for the area of a triangle, we'll be able to minimize the inradii lengths, and thus, eventually minimize the area of
formula for the area of a triangle, we'll be able to minimize the inradii lengths, and thus, eventually minimize the area of ![]() . (Proof needed here).
. (Proof needed here).
We need to minimize ![]() . Let
. Let ![]() ,
, ![]() , and
, and ![]() . After an application of Stewart's Theorem, we will get that
. After an application of Stewart's Theorem, we will get that ![]() To minimize this quadratic,
To minimize this quadratic, ![]() whereby we conclude that
whereby we conclude that ![]() .
.
From here, draw perpendiculars down from ![]() and
and ![]() to
to ![]() and
and ![]() respectively, and label the foot of these perpendiculars
respectively, and label the foot of these perpendiculars ![]() and
and ![]() respectively. After, draw the inradii from
respectively. After, draw the inradii from ![]() to
to ![]() , and from
, and from ![]() to
to ![]() , and draw in
, and draw in ![]() .
.
Label the foot of the inradii to ![]() and
and ![]() ,
, ![]() and
and ![]() , respectively. From here, we see that to find
, respectively. From here, we see that to find ![]() , we need to find
, we need to find ![]() , and subtract off the sum of
, and subtract off the sum of ![]() and
and ![]() .
.
![]() can be found by finding the area of two quadrilaterals
can be found by finding the area of two quadrilaterals ![]() as well as the area of a trapezoid
as well as the area of a trapezoid ![]() . If we let the inradius of
. If we let the inradius of ![]() be
be ![]() and if we let the inradius of
and if we let the inradius of ![]() be
be ![]() , we'll find, after an application of basic geometry and careful calculations on paper, that
, we'll find, after an application of basic geometry and careful calculations on paper, that ![]() .
.
The area of two triangles can be found in a similar fashion, however, we must use ![]() substitution to solve for
substitution to solve for ![]() as well as
as well as ![]() . After doing this, we'll get a similar sum in terms of
. After doing this, we'll get a similar sum in terms of ![]() and
and ![]() for the area of those two triangles which is equal to
for the area of those two triangles which is equal to ![]()
Now we're set. Summing up the area of the Hexagon and the two triangles and simplifying, we get that the formula for ![]() is just
is just ![\[[ABC]-\left(\frac{(35+3\sqrt{21})(r_1)}{2}+\frac{(45+3r_2\sqrt{21})(r_2)}{2}\right).\]](http://latex.artofproblemsolving.com/e/d/7/ed75de39d2544c5acbbad80d0d2c955f3e141ce6.png)
Using Heron's formula, ![]() . Solving for
. Solving for ![]() and
and ![]() using Heron's in
using Heron's in ![]() and
and ![]() , we get that
, we get that ![]() and
and ![]() . From here, we just have to plug into our above equation and solve.
. From here, we just have to plug into our above equation and solve.
Doing so gets us that the minimum area of ![]()
-Azeem H.(Mathislife52) ~edited by phoenixfire
Video Solution by Osman Nal
https://www.youtube.com/watch?v=sT-wxV2rYqs
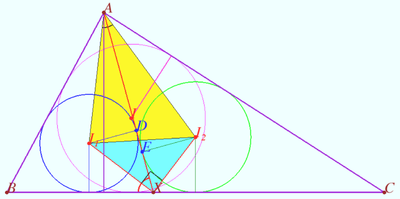
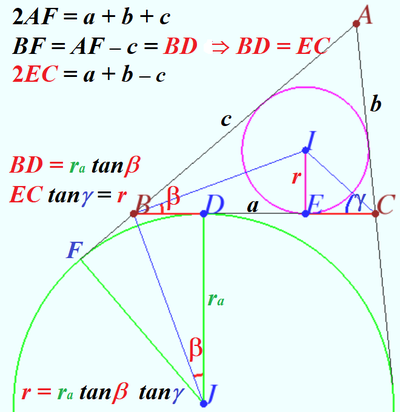
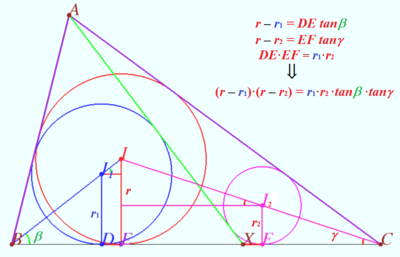
Solution 4 (Geometry only)
Let ![]() be semiperimeter of
be semiperimeter of ![]() be the height of
be the height of ![]() dropped from
dropped from ![]()
Let ![]() be inradius of the
be inradius of the ![]() and
and ![]() respectively.
respectively.
Using the Lemma (below), we get the area
![]()
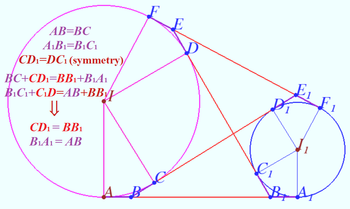
![]() Lemma
Lemma
![]()
Proof
![]() WLOG
WLOG ![]()
![]()
![]()
![]() if and only if
if and only if
Claim
![]() Proof
Proof
Let ![]()
![]()
![]()
![]()
![]()
![]()
![]() We use Cosine Law for
We use Cosine Law for ![]() and
and ![]() and get
and get
![]() Last is evident, the claim has been proven.
Last is evident, the claim has been proven.
vladimir.shelomovskii@gmail.com, vvsss
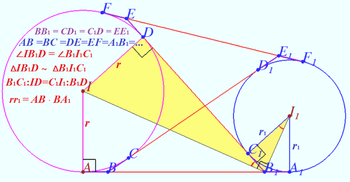
Solution 4a
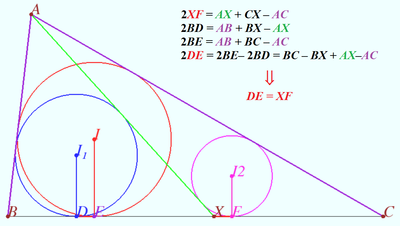
Geometry proof of the equation ![]()
![]()
Using diagrams, we can recall known facts and using those facts for making sequence of equations.
![]()
The twice area of ![]() is
is
![]()
![]()
Therefore ![]()
vladimir.shelomovskii@gmail.com, vvsss
Video Solution by MOP 2024
https://youtube.com/watch?v=ALzZA13PuZk
See Also
| 2018 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 12 |
Followed by Problem 14 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.