Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Feuerbach point"

(→‎Sharygin’s prove)
(→‎Sharygin’s proof)
 
(11 intermediate revisions by the same user not shown)
Line 1: Line 1:
 
The incircle and nine-point circle of a triangle are tangent to each other at the Feuerbach point of the triangle. The Feuerbach point is listed as X(11) in Clark Kimberling's Encyclopedia of Triangle Centers  and is named after Karl Wilhelm Feuerbach.
 
The incircle and nine-point circle of a triangle are tangent to each other at the Feuerbach point of the triangle. The Feuerbach point is listed as X(11) in Clark Kimberling's Encyclopedia of Triangle Centers  and is named after Karl Wilhelm Feuerbach.
−
==Sharygin’s prove==
+
==Sharygin’s proof==
 
<math>1998, 24^{th}</math> Russian math olympiad
 
<math>1998, 24^{th}</math> Russian math olympiad
 
[[File:Feuerbach 1.png|500px|right]]
 
[[File:Feuerbach 1.png|500px|right]]
−
<i><b>Claim 1</b></i>
+
===Claim 1===
−
 
 
 
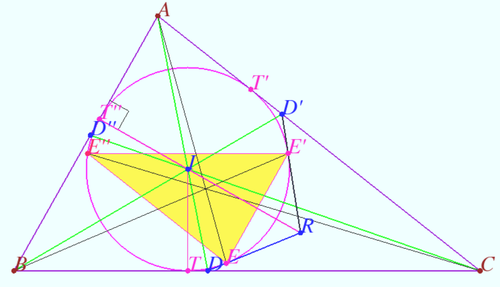
Let <math>D</math> be the base of the bisector of angle A of scalene triangle <math>\triangle ABC.</math>
 
Let <math>D</math> be the base of the bisector of angle A of scalene triangle <math>\triangle ABC.</math>
  
Line 18: Line 17:
 
WLOG, <math>\beta > \gamma.</math>
 
WLOG, <math>\beta > \gamma.</math>
 
<cmath>\angle TIT'' = 180^\circ - 2 \beta, \angle ADB = 180^\circ - \alpha - 2 \beta,</cmath>
 
<cmath>\angle TIT'' = 180^\circ - 2 \beta, \angle ADB = 180^\circ - \alpha - 2 \beta,</cmath>
−
<cmath>\angle DIT = 90^\circ - \angle ADB = \alpha + 2 \beta – 90^\circ = \beta -\gamma, \angle EID = \angle TID \implies</cmath>
+
<cmath>\angle DIT = 90^\circ - \angle ADB = \alpha + 2 \beta - 90^\circ = \beta -\gamma, \angle EID = \angle TID \implies</cmath>
 
<cmath>\angle T''IE = \angle T''IT + 2 \angle TID = 180^\circ - 2 \beta + 2(\beta - \gamma) = 180^\circ - 2 \gamma.</cmath>
 
<cmath>\angle T''IE = \angle T''IT + 2 \angle TID = 180^\circ - 2 \beta + 2(\beta - \gamma) = 180^\circ - 2 \gamma.</cmath>
 
Similarly, <math>\angle T''IE' = 180^\circ – 2 \gamma \implies</math> points <math>E</math> and <math>E'</math> are symmetric with respect <math>T''I \perp AB \implies AB || EE'.</math>
 
Similarly, <math>\angle T''IE' = 180^\circ – 2 \gamma \implies</math> points <math>E</math> and <math>E'</math> are symmetric with respect <math>T''I \perp AB \implies AB || EE'.</math>
Line 26: Line 25:
 
<math>AE, BE', CE''</math> are concurrent at the homothetic center of <math>\triangle ABC</math> and <math>\triangle EE'E''.</math>
 
<math>AE, BE', CE''</math> are concurrent at the homothetic center of <math>\triangle ABC</math> and <math>\triangle EE'E''.</math>
  
−
<i><b>Claim 2</b></i>
+
===Claim 2===
 
[[File:Feuerbach 2.png|500px|right]]
 
[[File:Feuerbach 2.png|500px|right]]
 
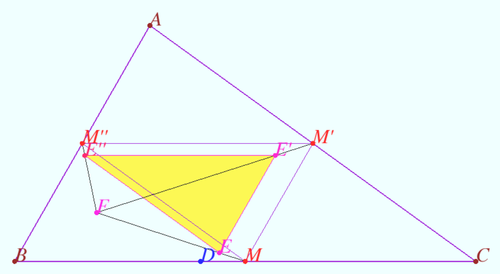
Let <math>M, M',</math> and <math>M''</math> be the midpoints <math>BC, AC,</math> and <math>AB,</math> respectively. Points <math>E, E',</math> and <math>E''</math> was defined at Claim 1.
 
Let <math>M, M',</math> and <math>M''</math> be the midpoints <math>BC, AC,</math> and <math>AB,</math> respectively. Points <math>E, E',</math> and <math>E''</math> was defined at Claim 1.
Line 37: Line 36:
 
<cmath>\triangle MM'M''  \sim \triangle EE'E'' \implies</cmath>
 
<cmath>\triangle MM'M''  \sim \triangle EE'E'' \implies</cmath>
 
<math>ME, M'E', M''E''</math> are concurrent at the homothetic center of <math>\triangle MM'M''</math> and <math>\triangle EE'E''.</math>
 
<math>ME, M'E', M''E''</math> are concurrent at the homothetic center of <math>\triangle MM'M''</math> and <math>\triangle EE'E''.</math>
 +
 +
===Claim 3===
 +
[[File:Feuerbach 3a.png|500px|right]]
 +
Let <math>H</math> be the base of height <math>AH.</math> Let <math>F_0 = ME \cap \omega \ne E.</math>
 +
Prove that points <math>F_0, E, D,</math> and <math>H</math> are concyclic.
 +
 +
<i><b>Proof</b></i>
 +
 +
<math>MT</math> tangent to <math>\omega \implies MT^2 = ME \cdot MF_0.</math>
 +
 +
Denote <math>a = BC, b = AC, c = AB.</math>
 +
<cmath>BD = \frac {ac}{b+c}, BM = \frac {a}{2} \implies MD = \frac {a(b-c)}{2(b+c)}.</cmath>
 +
<cmath>BT = \frac {a+c-b}{2} \implies MT = \frac {b-c}{2}.</cmath>
 +
Point <math>H</math> lies on radical axis of circles centered at <math>B</math> and <math>C</math> with the radii <math>c</math> and <math>b,</math> respectively.
 +
<cmath>BH = \frac {a}{2} - \frac {b^2 - c^2}{2a} \implies HM =  \frac {b^2 - c^2}{2a}.</cmath>
 +
Therefore <math>MH \cdot MD = MT^2 = ME \cdot MF_0 \implies</math> points <math>F_0, E, D,</math> and <math>H</math> are concyclic.
 +
 +
===Claim 4===
 +
[[File:Feuerbach 4.png|450px|right]]
 +
Prove that points <math>F_0, M, M',</math> and <math>H</math> are concyclic.
 +
 +
<i><b>Proof</b></i>
 +
 +
<cmath>\angle EDM = \angle TIE = 2 \angle TID = 2(\beta - \gamma).</cmath>
 +
<math>F_0, E, D,</math> and <math>H</math> are concyclic <math>\implies</math>
 +
<cmath>\angle EF_0H = \angle EDM = 2(\beta - \gamma) = \angle MF_0H.</cmath>
 +
<cmath>\angle M'HM = \angle ACB = 2 \gamma.</cmath>
 +
<cmath>MM'||AB \implies \angle M'MC = 2 \beta.</cmath>
 +
<cmath>\angle HM'M = \angle CMM' - \angle MHM' = 2\beta - 2 \gamma = \angle MF_0H \implies</cmath>
 +
points <math>F_0, M, M',</math> and <math>H</math> are concyclic.
 +
 +
===Sharygin’s proof===
 +
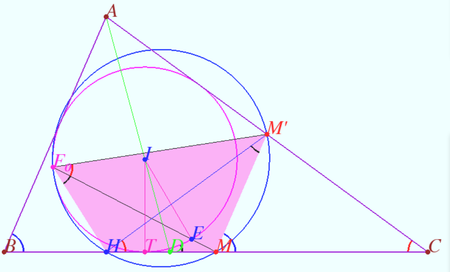
The incircle <math>\omega</math> and the nine-point circle <math>\Omega</math> of a triangle are tangent to each other.
 +
 +
<i><b>Proof</b></i>
 +
 +
Let <math>F_0 = ME \cap \omega \ne E, F' = M'E' \cap \omega \ne E', F'' = M''E'' \cap \omega \ne E''.</math>
 +
 +
According claim 4, each of this point lyes on <math>\Omega.</math>
 +
 +
<math>\omega</math> and <math>\Omega</math> have not more then two common point, so two of points <math>F_0, F',</math> and <math>F''</math> are coincide.
 +
 +
Therefore these two points coincide with point <math>F</math>  witch means that <math>F = \omega \cap \Omega.</math>
 +
 +
<math>F</math> is the center of similarity of <math>\omega</math> and <math>\Omega,</math> therefore there is no second point of intersection of <math>\omega</math> and <math>\Omega.</math>
 +
 +
We conclude that these circles are tangent to each other at point <math>F.</math>
 +
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''

Latest revision as of 09:23, 29 December 2023

The incircle and nine-point circle of a triangle are tangent to each other at the Feuerbach point of the triangle. The Feuerbach point is listed as X(11) in Clark Kimberling's Encyclopedia of Triangle Centers and is named after Karl Wilhelm Feuerbach.

Sharygin’s proof

$1998, 24^{th}$ Russian math olympiad

Feuerbach 1.png

Claim 1

Let $D$ be the base of the bisector of angle A of scalene triangle $\triangle ABC.$

Let $DE$ be a tangent different from side $BC$ to the incircle of $\triangle ABC (E$ is the point of tangency). Similarly, we denote $D', E', D'',$ and $E''.$

Prove that $EE'||AB, \triangle ABC \sim \triangle EE'E'', AE, BE', CE''$ are concurrent.

Proof

Let $T, T',$ and $T''$ be the point of tangency of the incircle $\omega$ and $BC, AC,$ and $AB.$

Let $\angle A = 2 \alpha, \angle B = 2 \beta, \angle C = 2 \gamma, \alpha + \beta + \gamma = 90^\circ.$ WLOG, $\beta > \gamma.$ \[\angle TIT'' = 180^\circ - 2 \beta, \angle ADB = 180^\circ - \alpha - 2 \beta,\] \[\angle DIT = 90^\circ - \angle ADB = \alpha + 2 \beta - 90^\circ = \beta -\gamma, \angle EID = \angle TID \implies\] \[\angle T''IE = \angle T''IT + 2 \angle TID = 180^\circ - 2 \beta + 2(\beta - \gamma) = 180^\circ - 2 \gamma.\] Similarly, $\angle T''IE' = 180^\circ – 2 \gamma \implies$ points $E$ and $E'$ are symmetric with respect $T''I \perp AB \implies AB || EE'.$

Similarly, $BC || E''E', AC || E''E \implies \triangle ABC \sim \triangle EE'E''.$

$AE, BE', CE''$ are concurrent at the homothetic center of $\triangle ABC$ and $\triangle EE'E''.$

Claim 2

Feuerbach 2.png

Let $M, M',$ and $M''$ be the midpoints $BC, AC,$ and $AB,$ respectively. Points $E, E',$ and $E''$ was defined at Claim 1.

Prove that $ME, M'E',$ and $M''E''$ are concurrent.

Proof

\[\triangle ABC \sim \triangle MM'M'' \implies\] \[\triangle MM'M'' \sim \triangle EE'E'' \implies\] $ME, M'E', M''E''$ are concurrent at the homothetic center of $\triangle MM'M''$ and $\triangle EE'E''.$

Claim 3

Feuerbach 3a.png

Let $H$ be the base of height $AH.$ Let $F_0 = ME \cap \omega \ne E.$ Prove that points $F_0, E, D,$ and $H$ are concyclic.

Proof

$MT$ tangent to $\omega \implies MT^2 = ME \cdot MF_0.$

Denote $a = BC, b = AC, c = AB.$ \[BD = \frac {ac}{b+c}, BM = \frac {a}{2} \implies MD = \frac {a(b-c)}{2(b+c)}.\] \[BT = \frac {a+c-b}{2} \implies MT = \frac {b-c}{2}.\] Point $H$ lies on radical axis of circles centered at $B$ and $C$ with the radii $c$ and $b,$ respectively. \[BH = \frac {a}{2} - \frac {b^2 - c^2}{2a} \implies HM = \frac {b^2 - c^2}{2a}.\] Therefore $MH \cdot MD = MT^2 = ME \cdot MF_0 \implies$ points $F_0, E, D,$ and $H$ are concyclic.

Claim 4

Feuerbach 4.png

Prove that points $F_0, M, M',$ and $H$ are concyclic.

Proof

\[\angle EDM = \angle TIE = 2 \angle TID = 2(\beta - \gamma).\] $F_0, E, D,$ and $H$ are concyclic $\implies$ \[\angle EF_0H = \angle EDM = 2(\beta - \gamma) = \angle MF_0H.\] \[\angle M'HM = \angle ACB = 2 \gamma.\] \[MM'||AB \implies \angle M'MC = 2 \beta.\] \[\angle HM'M = \angle CMM' - \angle MHM' = 2\beta - 2 \gamma = \angle MF_0H \implies\] points $F_0, M, M',$ and $H$ are concyclic.

Sharygin’s proof

The incircle $\omega$ and the nine-point circle $\Omega$ of a triangle are tangent to each other.

Proof

Let $F_0 = ME \cap \omega \ne E, F' = M'E' \cap \omega \ne E', F'' = M''E'' \cap \omega \ne E''.$

According claim 4, each of this point lyes on $\Omega.$

$\omega$ and $\Omega$ have not more then two common point, so two of points $F_0, F',$ and $F''$ are coincide.

Therefore these two points coincide with point $F$ witch means that $F = \omega \cap \Omega.$

$F$ is the center of similarity of $\omega$ and $\Omega,$ therefore there is no second point of intersection of $\omega$ and $\Omega.$

We conclude that these circles are tangent to each other at point $F.$

vladimir.shelomovskii@gmail.com, vvsss

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Feuerbach_point&oldid=208655"