Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2023 AMC 12B Problems/Problem 7"

(latex)
(→‎Solution 2 (3 degree polynominal graph))
 
(8 intermediate revisions by 6 users not shown)
Line 2: Line 2:
 
For how many integers <math>n</math> does the expression<cmath>\sqrt{\frac{\log (n^2) - (\log n)^2}{\log n - 3}}</cmath>represent a real number, where log denotes the base <math>10</math> logarithm?
 
For how many integers <math>n</math> does the expression<cmath>\sqrt{\frac{\log (n^2) - (\log n)^2}{\log n - 3}}</cmath>represent a real number, where log denotes the base <math>10</math> logarithm?
  
−
<math>\textbf{(A) }900 \qquad \textbf{(B) }2\qquad \textbf{(C) }902 \qquad \textbf{(D) } 2  \qquad \textbf{(E) }901</math>
+
<math>\textbf{(A) }900 \qquad \textbf{(B) }3\qquad \textbf{(C) }902 \qquad \textbf{(D) } 2  \qquad \textbf{(E) }901</math>
  
 
==Solution==
 
==Solution==
Line 36: Line 36:
 
==Solution (Solution 1 for dummies)==
 
==Solution (Solution 1 for dummies)==
  
−
Notice <math>\log(n^2)</math> can be written as <math>2log(n)</math>. Setting <math>a=log(n)</math>, the equation becomes <math>\sqrt{\frac{2a-a^2}{a-3}}</math> which can be written as <math>\sqrt{\frac{a(a-2)}{a-3}}</math>
+
Notice <math>\log(n^2)</math> can be written as <math>2\log(n)</math>. Setting <math>a=\log(n)</math>, the equation becomes <math>\sqrt{\frac{2a-a^2}{a-3}}</math> which can be written as <math>\sqrt{\frac{a(2-a)}{a-3}}</math>
  
 
Case 1: <math>a \ge 3</math>
 
Case 1: <math>a \ge 3</math>
−
The expression is undefined when <math>a=3</math>. For <math>a>3</math>, it is trivial to see that the denominator is negative and the numerator is positive, thus resulting in no real solutions.
+
The expression is undefined when <math>a=3</math>. For <math>a>3</math>, it is trivial to see that the denominator is positive and the numerator is negative, thus resulting in no real solutions.
  
 
Case 2: <math>2 \le a<3</math>
 
Case 2: <math>2 \le a<3</math>
Line 45: Line 45:
  
 
Case 3: <math>0<a<2</math>
 
Case 3: <math>0<a<2</math>
−
The numerator will be negative but the denominator is positive, no real solutions exist.  
+
The numerator will be positive but the denominator is negative, no real solutions exist.  
  
 
Case 4: <math>a=0</math>
 
Case 4: <math>a=0</math>
Line 55: Line 55:
 
Adding up the cases:
 
Adding up the cases:
 
<math>900+1=\boxed{\textbf{(E) 901}}</math>
 
<math>900+1=\boxed{\textbf{(E) 901}}</math>
−
 
−
Side Note: Someone please fix this to make it readable. I don't know anything about latex.
 
  
 
~woeIsMe
 
~woeIsMe
 
typesetting: paras
 
typesetting: paras
 +
 +
 +
==Solution 3 (3 degree polynominal graph) ==
 +
 +
for <math>\frac{a(2-a)}{a-3} >0  </math> ,
 +
 +
transform it into a(a-2)(a-3) <0 ,
 +
 +
use the following graph to quickly confirm
 +
 +
1) a < 0 or
 +
 +
2) 2 < a <3
 +
 +
~[https://artofproblemsolving.com/wiki/index.php/User:Cyantist luckuso]
 +
 +
[[Image:2023_AMC12B_P7.PNG|thumb|center|600px]]
 +
 +
==Video Solution==
 +
 +
https://youtu.be/GGdJJzzbivM
 +
 +
 +
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
  
 
==See Also==
 
==See Also==
 
{{AMC12 box|year=2023|ab=B|num-b=6|num-a=8}}
 
{{AMC12 box|year=2023|ab=B|num-b=6|num-a=8}}
 
{{MAA Notice}}
 
{{MAA Notice}}

Latest revision as of 21:08, 19 August 2024

Problem

For how many integers $n$ does the expression\[\sqrt{\frac{\log (n^2) - (\log n)^2}{\log n - 3}}\]represent a real number, where log denotes the base $10$ logarithm?

$\textbf{(A) }900 \qquad \textbf{(B) }3\qquad \textbf{(C) }902 \qquad \textbf{(D) } 2 \qquad \textbf{(E) }901$

Solution

We have \begin{align*} \sqrt{\frac{\log \left( n^2 \right) - \left( \log n \right)^2}{\log n - 3}} & = \sqrt{\frac{2 \log n - \left( \log n \right)^2}{\log n - 3}} \\ & = \sqrt{\frac{\left( \log n \right) \left( 2 - \log n\right)}{\log n - 3}} . \end{align*}

Because $n$ is an integer and $\log n$ is well defined, $n$ must be a positive integer.

Case 1: $n = 1$ or $10^2$.

The above expression is 0. So these are valid solutions.

Case 2: $n \neq 1, 10^2$.

Thus, $\log n > 0$ and $2 - \log n \neq 0$. To make the above expression real, we must have $2 < \log n < 3$. Thus, $100 < n < 1000$. Thus, $101 \leq n \leq 999$. Hence, the number of solutions in this case is 899.

Putting all cases together, the total number of solutions is $\boxed{\textbf{(E) 901}}$.

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

Solution (Solution 1 for dummies)

Notice $\log(n^2)$ can be written as $2\log(n)$. Setting $a=\log(n)$, the equation becomes $\sqrt{\frac{2a-a^2}{a-3}}$ which can be written as $\sqrt{\frac{a(2-a)}{a-3}}$

Case 1: $a \ge 3$ The expression is undefined when $a=3$. For $a>3$, it is trivial to see that the denominator is positive and the numerator is negative, thus resulting in no real solutions.

Case 2: $2 \le a<3$ For $a=2$, the numerator is zero, giving us a valid solution. When $a>2$, both the denominator and numerator are negative so all real values of a in this interval is a solution to the equation. All integers of n that makes this true are between $10^2$ and $10^3-1$. There are 900 solutions here.

Case 3: $0<a<2$ The numerator will be positive but the denominator is negative, no real solutions exist.

Case 4: $a=0$ The expression evaluates to zero, $1$ valid solution exists.

Case 5: $a<0$ All values for $a<0$ requires $0<n<1$, no integer solutions exist.

Adding up the cases: $900+1=\boxed{\textbf{(E) 901}}$

~woeIsMe typesetting: paras


Solution 3 (3 degree polynominal graph)

for $\frac{a(2-a)}{a-3} >0$ ,

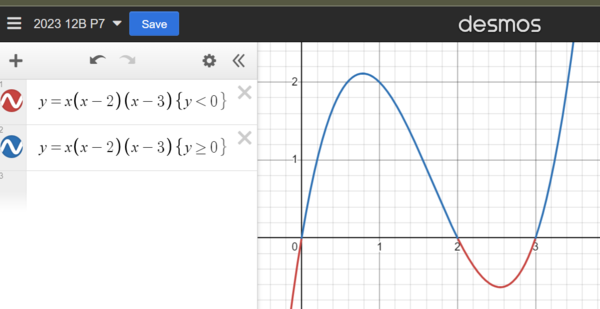
transform it into a(a-2)(a-3) <0 ,

use the following graph to quickly confirm

1) a < 0 or

2) 2 < a <3

~luckuso

2023 AMC12B P7.PNG

Video Solution

https://youtu.be/GGdJJzzbivM


~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

See Also

2023 AMC 12B (Problems • Answer Key • Resources)
Preceded by
Problem 6 		Followed by
Problem 8
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2023_AMC_12B_Problems/Problem_7&oldid=225353"