Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2023 AMC 12B Problems/Problem 17"

(→‎Solution)
m (→‎Video Solution)
 
(17 intermediate revisions by 6 users not shown)
Line 1: Line 1:
−
==Solution==
+
==Problem==
 +
Triangle <math>ABC</math> has side lengths in arithmetic progression, and the smallest side has length <math>6.</math> If the triangle has an angle of <math>120^\circ,</math> what is the area of <math>ABC</math>?
 +
 
 +
<math>\textbf{(A) }12\sqrt{3}\qquad\textbf{(B) }8\sqrt{6}\qquad\textbf{(C) }14\sqrt{2}\qquad\textbf{(D) }20\sqrt{2}\qquad\textbf{(E) }15\sqrt{3}</math>
 +
 
 +
==Solution 1==
  
 
The length of the side opposite to the angle with <math>120^\circ</math> is longest.  
 
The length of the side opposite to the angle with <math>120^\circ</math> is longest.  
Line 27: Line 32:
  
 
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
 
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
 +
 +
==Solution 2==
 +
Let the side lengths of <math>\triangle ABC</math> be <math>6</math>, <math>x</math>, and <math>2x-6</math>, where <math>6 \le x \le 2x-6</math>. As <math>2x-6</math> is the longest side, the angle opposite to it will be <math>120^{\circ}</math>.
 +
 +
By the law of Cosine
 +
<cmath>(2x-6)^2 = 6^2 + x^2 - 2 \cdot 6 \cdot x \cdot \cos 120^{\circ}</cmath>
 +
<cmath>4x^2 - 24x + 36 = 36 + x^2 + 6x</cmath><cmath>3x^2 - 30x = 0</cmath>
 +
<cmath>x^2 - 10x = 0</cmath>
 +
As <math>x \neq 0</math>, <math>x = 10</math>.
 +
 +
Therefore, <math>[ABC] = \frac{ 6 \cdot 10 \cdot \sin 120^{\circ} }{2} = \boxed{\textbf{(E) } 15 \sqrt{3}}</math>
 +
 +
~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]
 +
 +
==Solution 3==
 +
Let the side lengths of <math>\triangle ABC</math> be <math>6</math>, <math>6+d</math>, and <math>6+2d</math>, where <math>6 \le 6+d \le 6+2d</math>. As <math>6+2d</math> is the longest side, the angle opposite to it will be <math>120^{\circ}</math>.
 +
 +
By the law of Cosine
 +
<cmath>(6+2d)^2 = 6^2 + (6+d)^2 - 2 \cdot 6 \cdot (6+d) \cdot \cos 120^{\circ}</cmath>
 +
<cmath>4d^2 + 24d + 36 = 36 + 36 + 12 d + d^2 + 36 + 6d</cmath>
 +
<cmath>3d^2 + 6d - 72 = 0</cmath>
 +
<cmath>d^2 + 2d - 24 = 0</cmath>
 +
<cmath>(d+6)(d-4)=0</cmath>
 +
As <math>d \ge 0</math>, <math>d = 4</math>, <math>6+d = 10</math>
 +
 +
Therefore, <math>[ABC] = \frac{ 6 \cdot 10 \cdot \sin 120^{\circ} }{2} = \boxed{\textbf{(E) } 15 \sqrt{3}}</math>
 +
 +
~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]
 +
 +
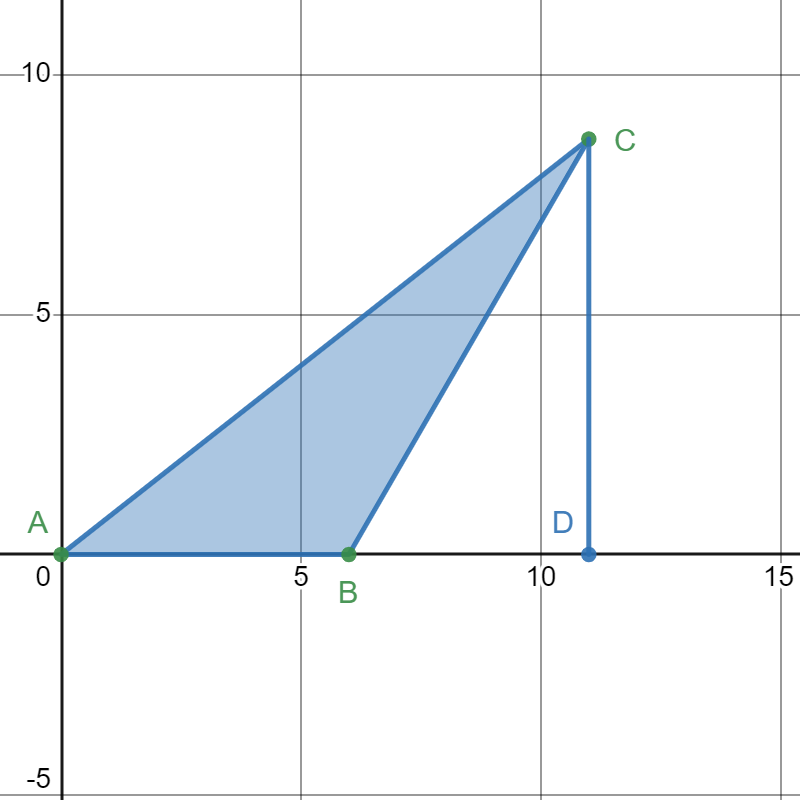
==Solution 4 (Analytic Geometry)==
 +
 +
Since the triangle's longest side must correspond to the <math>120^\circ</math> angle, the triangle is unique. By analytic geometry, we construct the following plot.
 +
 +
[[File:PJ_2023_12B_Q17.png]]
 +
 +
We know the coordinates of point <math>A</math> being the origin and <math>B</math> being <math>(6,0)</math>. Constructing the line which point <math>C</math> can lay on, here since <math>\angle B=120^\circ</math>, <math>C</math> is on the line <cmath>y=\sqrt{3}\left(x-6\right).</cmath>
 +
 +
I denote <math>D</math> as the perpendicular line from <math>C</math> to <math>AB</math>, and assume <math>CD=k</math>. Here we know <math>\triangle BCD</math> is a <math>30^\circ-60^\circ-90^\circ</math> triangle. Hence <math>DC=\sqrt{3}k</math> and <math>BC=2k</math>.
 +
 +
Furthermore, due to the arithmetic progression, we know <math>AC=4k-6</math>. Hence, in <math>\triangle ACD</math>, <cmath>\left(4k-6\right)^{2}=\left(6+k\right)^{2}+3k^{2},</cmath> <cmath>k=5.</cmath>
 +
 +
Thus, the area is equal to <math>\frac{1}{2}\cdot 6\cdot \sqrt{3} k=\boxed{\textbf{(E) } 15 \sqrt{3}}</math>.
 +
 +
~Prof. Joker
 +
 +
==Video Solution 1 by OmegaLearn==
 +
https://youtu.be/uVHCLHBWWJM
 +
 +
==Video Solution 2==
 +
 +
https://youtu.be/3w59Hikefqs
 +
 +
 +
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
 +
 +
==See Also==
 +
{{AMC12 box|year=2023|ab=B|num-b=16|num-a=18}}
 +
{{MAA Notice}}

Latest revision as of 08:52, 4 December 2023

Problem

Triangle $ABC$ has side lengths in arithmetic progression, and the smallest side has length $6.$ If the triangle has an angle of $120^\circ,$ what is the area of $ABC$?

$\textbf{(A) }12\sqrt{3}\qquad\textbf{(B) }8\sqrt{6}\qquad\textbf{(C) }14\sqrt{2}\qquad\textbf{(D) }20\sqrt{2}\qquad\textbf{(E) }15\sqrt{3}$

Solution 1

The length of the side opposite to the angle with $120^\circ$ is longest. We denote its value as $x$.

Because three side lengths form an arithmetic sequence, the middle-valued side length is $\frac{x + 6}{2}$.

Following from the law of cosines, we have \begin{align*} 6^2 + \left( \frac{x + 6}{2} \right)^2 - 2 \cdot 6 \cdot \frac{x + 6}{2} \cdot \cos 120^\circ = x^2 . \end{align*}

By solving this equation, we get $x = 14$. Thus, $\frac{x + 6}{2} = 10$.

Therefore, the area of the triangle is \begin{align*} \frac{1}{2} 6 \cdot 10 \cdot \sin 120^\circ = \boxed{\textbf{(E) } 15 \sqrt{3}} . \end{align*}

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

Solution 2

Let the side lengths of $\triangle ABC$ be $6$, $x$, and $2x-6$, where $6 \le x \le 2x-6$. As $2x-6$ is the longest side, the angle opposite to it will be $120^{\circ}$.

By the law of Cosine \[(2x-6)^2 = 6^2 + x^2 - 2 \cdot 6 \cdot x \cdot \cos 120^{\circ}\] \[4x^2 - 24x + 36 = 36 + x^2 + 6x\]\[3x^2 - 30x = 0\] \[x^2 - 10x = 0\] As $x \neq 0$, $x = 10$.

Therefore, $[ABC] = \frac{ 6 \cdot 10 \cdot \sin 120^{\circ} }{2} = \boxed{\textbf{(E) } 15 \sqrt{3}}$

~isabelchen

Solution 3

Let the side lengths of $\triangle ABC$ be $6$, $6+d$, and $6+2d$, where $6 \le 6+d \le 6+2d$. As $6+2d$ is the longest side, the angle opposite to it will be $120^{\circ}$.

By the law of Cosine \[(6+2d)^2 = 6^2 + (6+d)^2 - 2 \cdot 6 \cdot (6+d) \cdot \cos 120^{\circ}\] \[4d^2 + 24d + 36 = 36 + 36 + 12 d + d^2 + 36 + 6d\] \[3d^2 + 6d - 72 = 0\] \[d^2 + 2d - 24 = 0\] \[(d+6)(d-4)=0\] As $d \ge 0$, $d = 4$, $6+d = 10$

Therefore, $[ABC] = \frac{ 6 \cdot 10 \cdot \sin 120^{\circ} }{2} = \boxed{\textbf{(E) } 15 \sqrt{3}}$

~isabelchen

Solution 4 (Analytic Geometry)

Since the triangle's longest side must correspond to the $120^\circ$ angle, the triangle is unique. By analytic geometry, we construct the following plot.

PJ 2023 12B Q17.png

We know the coordinates of point $A$ being the origin and $B$ being $(6,0)$. Constructing the line which point $C$ can lay on, here since $\angle B=120^\circ$, $C$ is on the line \[y=\sqrt{3}\left(x-6\right).\]

I denote $D$ as the perpendicular line from $C$ to $AB$, and assume $CD=k$. Here we know $\triangle BCD$ is a $30^\circ-60^\circ-90^\circ$ triangle. Hence $DC=\sqrt{3}k$ and $BC=2k$.

Furthermore, due to the arithmetic progression, we know $AC=4k-6$. Hence, in $\triangle ACD$, \[\left(4k-6\right)^{2}=\left(6+k\right)^{2}+3k^{2},\] \[k=5.\]

Thus, the area is equal to $\frac{1}{2}\cdot 6\cdot \sqrt{3} k=\boxed{\textbf{(E) } 15 \sqrt{3}}$.

~Prof. Joker

Video Solution 1 by OmegaLearn

https://youtu.be/uVHCLHBWWJM

Video Solution 2

https://youtu.be/3w59Hikefqs


~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

See Also

2023 AMC 12B (Problems • Answer Key • Resources)
Preceded by
Problem 16 		Followed by
Problem 18
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2023_AMC_12B_Problems/Problem_17&oldid=206472"