Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2022 AMC 8 Problems/Problem 25"

m (→‎Video Solution)
(→‎Video Solution)
 
(48 intermediate revisions by 16 users not shown)
Line 48: Line 48:
 
~mahaler
 
~mahaler
  
−
==Solution 3 (Recursion)==
+
==Solution 3 (Complement)==
 +
There are always three possible leaves to jump to every time the cricket decides to jump, so there is a total number of <math> 3^4 </math> routes. Let <math>A</math> denote the leaf cricket starts at, and <math>B, C, D</math> be the other leaves. If we want the cricket to move to leaf <math> A </math> for its last jump, the cricket cannot jump to leaf <math> A </math> for its third jump. Also, considering that the cricket starts at leaf <math> A </math>, he cannot jump to leaf <math> A </math> for its first jump. Note that there are <math> 3\cdot2=6 </math> paths if the cricket moves to leaf <math> A </math> for its third jump. Therefore, we can conclude that the total number of possible paths for the cricket to return to leaf <math> A </math> after four jumps is <math> 3^3 - 6 = 21 </math>, so the answer is <math> \frac{21}{3^4} = \frac{21}{81}=\boxed{\textbf{(E) }\frac{7}{27}} </math>.
 +
 
 +
~[[User:Bloggish|Bloggish]]
 +
 
 +
==Solution 4 (Recursion)==
  
 
Denote <math>P_n</math> to be the probability that the cricket would return back to the first point after <math>n</math> hops. Then, we get the recursive formula <cmath>P_n = \frac13(1-P_{n-1})</cmath> because if the leaf is not on the target leaf, then there is a <math>\frac13</math> probability that it will make it back.
 
Denote <math>P_n</math> to be the probability that the cricket would return back to the first point after <math>n</math> hops. Then, we get the recursive formula <cmath>P_n = \frac13(1-P_{n-1})</cmath> because if the leaf is not on the target leaf, then there is a <math>\frac13</math> probability that it will make it back.
Line 56: Line 61:
 
~wamofan
 
~wamofan
  
−
==Solution 4 (Dynamic Programming)==
+
==Solution 5 (Dynamic Programming)==
  
 
Let <math>A</math> denote the leaf cricket starts at, and <math>B, C, D</math> be the other leaves, similar to Solution 2.
 
Let <math>A</math> denote the leaf cricket starts at, and <math>B, C, D</math> be the other leaves, similar to Solution 2.
  
−
Let <math>A(n)</math> be the probability the cricket lands on <math>A</math> after <math>n</math> hops, <math>B(n)</math> be the probability the cricket lands on <math>B</math> after crawling <math>n</math> hops, and etc.
+
Let <math>A(n)</math> be the probability the cricket lands on <math>A</math> after <math>n</math> hops, <math>B(n)</math> be the probability the cricket lands on <math>B</math> after crawling <math>n</math> hops, etc.
  
 
Note that <math>A(1)=0</math> and <math>B(1)=C(1)=D(1)=\frac13.</math> For <math>n\geq2,</math> the probability that the cricket land on each leaf after <math>n</math> hops is <math>\frac13</math> the sum of the probability the cricket land on other leaves after <math>n-1</math> hops. So, we have
 
Note that <math>A(1)=0</math> and <math>B(1)=C(1)=D(1)=\frac13.</math> For <math>n\geq2,</math> the probability that the cricket land on each leaf after <math>n</math> hops is <math>\frac13</math> the sum of the probability the cricket land on other leaves after <math>n-1</math> hops. So, we have
Line 89: Line 94:
 
~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]
 
~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]
  
−
==Solution 5 (Generating Function)==
+
==Solution 6 (Generating Function)==
  
 
Assign the leaves to <math>0, 1, 2,</math> and <math>3</math> modulo <math>4,</math> and let <math>0</math> be the starting leaf. We then use generating functions with relation to the change of leaves. For example, from <math>3</math> to <math>1</math> would be a change of <math>2,</math> and from <math>1</math> to <math>2</math> would be a change of <math>1.</math> This generating function is equal to <math>(x+x^2+x^3)^4.</math> It is clear that we want the coefficients in the form of <math>x^{4n},</math> where <math>n</math> is a positive integer. One application of roots of unity filter gives us a successful case count of <math>\frac{81+1+1+1}{4} = 21.</math>
 
Assign the leaves to <math>0, 1, 2,</math> and <math>3</math> modulo <math>4,</math> and let <math>0</math> be the starting leaf. We then use generating functions with relation to the change of leaves. For example, from <math>3</math> to <math>1</math> would be a change of <math>2,</math> and from <math>1</math> to <math>2</math> would be a change of <math>1.</math> This generating function is equal to <math>(x+x^2+x^3)^4.</math> It is clear that we want the coefficients in the form of <math>x^{4n},</math> where <math>n</math> is a positive integer. One application of roots of unity filter gives us a successful case count of <math>\frac{81+1+1+1}{4} = 21.</math>
Line 97: Line 102:
 
~sigma
 
~sigma
  
−
==Solution 6 (Casework)==
+
==Solution 7 (Also Generating Functions)==
−
Let <math>A</math> be the leaf where the cricket was originally on. Note that the 3rd hop cannot be on <math>A</math>.
+
 
 +
Let the leaves be <math>(0,0), (0,1), (1,0),</math> and <math>(1,1)</math> on the coordinate plane, with the cricket starting at <math>(0,0)</math>. Then we write a generating function. We denote <math>x</math> a change in the x-value of the cricket, and similarly for <math>y</math>. Then our generating function is <math>(x+y+xy)^4,</math> and we wish to compute the number of terms in which the exponents of both x and y are even. To do this, we first square to get <math>(x^2 + y^2 + x^2y^2 + 2xy + 2x^2y + 2xy^2)^2</math>. Note that every term squared will give even powers for x and y, so that gives us <math>3 + 4\cdot3 = 15.</math> Then every combination of <math>x^2, y^2,</math> and <math>x^2y^2</math> will also give us even powers for x and y, so that yields <math>6</math> more terms, for a total of <math>21.</math> Now in total there <math>3^4 = 81</math> possible sequences, so <math>21/81</math> gives us the answer of <math>\boxed{\textbf{(E) }\frac{7}{27}}.</math>
 +
 
 +
~littlefox_amc
  
−
We form 2 cases.
+
==Remark==
  
−
'''Case 1: The cricket hops on the 3 leaves that don't include <math>A</math> for the 1st, 2nd, and 3rd hop.'''
+
This problem is a reduced version of [https://artofproblemsolving.com/wiki/index.php/1985_AIME_Problems/Problem_12 1985 AIME Problem 12], changing <math>7</math> steps into <math>4</math> steps.
  
−
There are <math>3</math> choices for the 1st hop, <math>2</math> for the 2nd, <math>2</math> for the 3rd, and <math>1</math> for the 4th (the cricket has to return). In total, <math>3 \cdot 2 \cdot 2 \cdot 1 = 12</math>.
+
This problem is also similar to [https://artofproblemsolving.com/wiki/index.php/2003_AIME_II_Problems/Problem_13 2003 AIME II Problem 13].
  
−
'''Case 2: The cricket returns to <math>A</math> on the 2nd hop.'''
+
~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]
  
−
There are <math>3</math> choices for the 1st hop, <math>1</math> for the 2nd (it has to return), <math>3</math> for the 3rd, and <math>1</math> for the 4th. We get <math>3 \cdot 1 \cdot 3 \cdot 1 = 9</math>.
+
==Video Solution by Math-X (First understand the problem!!!)==
 +
https://youtu.be/oUEa7AjMF2A?si=n9aPrcW_qLqFC8IF&t=5261
  
−
Since there are a total of <math>3^4 = 81</math> paths, the probability is <math>\frac{9+12}{81}=\frac{21}{81}=\boxed{\textbf{(E) }\frac{7}{27}}</math>.
+
~Math-X
  
−
~MrThinker
+
==Video Solution(🚀Under 2 min🚀 Easy logic with all paths color-coded ✨)==
 +
https://youtu.be/YiI9szmMWX4
  
−
==Remark==
+
<i>~Education, the Study of Everything</i>
  
−
This problem is a reduced version of [https://artofproblemsolving.com/wiki/index.php/1985_AIME_Problems/Problem_12 1985 AIME Problem 12], changing <math>7</math> steps into <math>4</math> steps.
+
==Video Solution==
 +
https://youtu.be/GNFG4cmYDgw
  
−
This problem is also similar to [https://artofproblemsolving.com/wiki/index.php/2003_AIME_II_Problems/Problem_13 2003 AIME II Problem 13].
+
Please like and subscribe!
 +
== Video Solution by OmegaLearn ==
 +
https://youtu.be/kE15Sy0B2Pk?t=633
  
−
~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]
+
~ pi_is_3.14
  
 
==Video Solution==
 
==Video Solution==
−
https://www.youtube.com/watch?v=8EQRGf9GQPU
+
https://www.youtube.com/watch?v=85A6av3oqRo
  
 
~Mathematical Dexterity
 
~Mathematical Dexterity
−
 
 
==Video Solution==
 
==Video Solution==
−
https://www.youtube.com/watch?v=hWvM6de6mG8
+
https://youtu.be/Ij9pAy6tQSg?t=2588
  
 
~Interstigation
 
~Interstigation
Line 134: Line 146:
 
==Video Solution==
 
==Video Solution==
 
https://www.youtube.com/watch?v=H1zxrkq6DKg
 
https://www.youtube.com/watch?v=H1zxrkq6DKg
 +
 +
~David
  
 
==Video Solution==
 
==Video Solution==
Line 144: Line 158:
  
 
~savannahsolver
 
~savannahsolver
 +
 +
== Video Solution Using States by SpreadTheMathLove ==
 +
https://www.youtube.com/watch?v=740Z355PtWs&t=777s
  
 
==See Also==  
 
==See Also==  
 
{{AMC8 box|year=2022|num-b=24|after=Last Problem}}
 
{{AMC8 box|year=2022|num-b=24|after=Last Problem}}
 
{{MAA Notice}}
 
{{MAA Notice}}

Latest revision as of 20:43, 2 June 2024

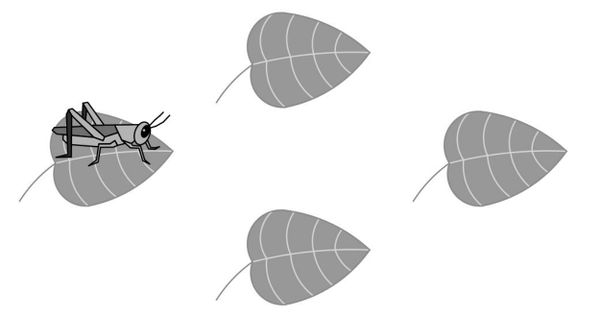
Problem

A cricket randomly hops between $4$ leaves, on each turn hopping to one of the other $3$ leaves with equal probability. After $4$ hops what is the probability that the cricket has returned to the leaf where it started?

2022 AMC 8 Problem 25 Picture.jpg

$\textbf{(A) }\frac{2}{9}\qquad\textbf{(B) }\frac{19}{80}\qquad\textbf{(C) }\frac{20}{81}\qquad\textbf{(D) }\frac{1}{4}\qquad\textbf{(E) }\frac{7}{27}$

Solution 1 (Casework)

Let $A$ denote the leaf where the cricket starts and $B$ denote one of the other $3$ leaves. Note that:

  • If the cricket is at $A,$ then the probability that it hops to $B$ next is $1.$
  • If the cricket is at $B,$ then the probability that it hops to $A$ next is $\frac13.$
  • If the cricket is at $B,$ then the probability that it hops to $B$ next is $\frac23.$

We apply casework to the possible paths of the cricket:

  1. $A \rightarrow B \rightarrow A \rightarrow B \rightarrow A$

    The probability for this case is $1\cdot\frac13\cdot1\cdot\frac13=\frac19.$

  2. $A \rightarrow B \rightarrow B \rightarrow B \rightarrow A$

    The probability for this case is $1\cdot\frac23\cdot\frac23\cdot\frac13=\frac{4}{27}.$

Together, the probability that the cricket returns to $A$ after $4$ hops is $\frac19+\frac{4}{27}=\boxed{\textbf{(E) }\frac{7}{27}}.$

~MRENTHUSIASM

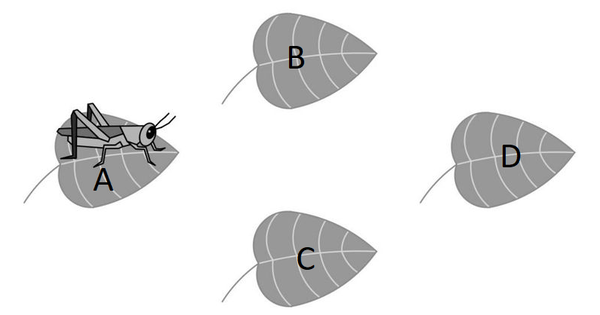
Solution 2 (Casework)

We can label the leaves as shown below:

2022 AMC 8 Problem 25 Picture 2.png

Carefully counting cases, we see that there are $7$ ways for the cricket to return to leaf $A$ after four hops if its first hop was to leaf $B$:

  1. $A \rightarrow B \rightarrow A \rightarrow B \rightarrow A$

  2. $A \rightarrow B \rightarrow A \rightarrow C \rightarrow A$

  3. $A \rightarrow B \rightarrow A \rightarrow D \rightarrow A$

  4. $A \rightarrow B \rightarrow C \rightarrow B \rightarrow A$

  5. $A \rightarrow B \rightarrow C \rightarrow D \rightarrow A$

  6. $A \rightarrow B \rightarrow D \rightarrow B \rightarrow A$

  7. $A \rightarrow B \rightarrow D \rightarrow C \rightarrow A$

By symmetry, we know that there are $7$ ways if the cricket's first hop was to leaf $C$, and there are $7$ ways if the cricket's first hop was to leaf $D$. So, there are $21$ ways in total for the cricket to return to leaf $A$ after four hops.

Since there are $3^4 = 81$ possible ways altogether for the cricket to hop to any other leaf four times, the answer is $\frac{21}{81} = \boxed{\textbf{(E) }\frac{7}{27}}$.

~mahaler

Solution 3 (Complement)

There are always three possible leaves to jump to every time the cricket decides to jump, so there is a total number of $3^4$ routes. Let $A$ denote the leaf cricket starts at, and $B, C, D$ be the other leaves. If we want the cricket to move to leaf $A$ for its last jump, the cricket cannot jump to leaf $A$ for its third jump. Also, considering that the cricket starts at leaf $A$, he cannot jump to leaf $A$ for its first jump. Note that there are $3\cdot2=6$ paths if the cricket moves to leaf $A$ for its third jump. Therefore, we can conclude that the total number of possible paths for the cricket to return to leaf $A$ after four jumps is $3^3 - 6 = 21$, so the answer is $\frac{21}{3^4} = \frac{21}{81}=\boxed{\textbf{(E) }\frac{7}{27}}$.

~Bloggish

Solution 4 (Recursion)

Denote $P_n$ to be the probability that the cricket would return back to the first point after $n$ hops. Then, we get the recursive formula \[P_n = \frac13(1-P_{n-1})\] because if the leaf is not on the target leaf, then there is a $\frac13$ probability that it will make it back.

With this formula and the fact that $P_1=0$ (After one hop, the cricket can never be back to the target leaf.), we have \[P_2 = \frac13, P_3 = \frac29, P_4 = \frac7{27},\] so our answer is $\boxed{\textbf{(E) }\frac{7}{27}}$.

~wamofan

Solution 5 (Dynamic Programming)

Let $A$ denote the leaf cricket starts at, and $B, C, D$ be the other leaves, similar to Solution 2.

Let $A(n)$ be the probability the cricket lands on $A$ after $n$ hops, $B(n)$ be the probability the cricket lands on $B$ after crawling $n$ hops, etc.

Note that $A(1)=0$ and $B(1)=C(1)=D(1)=\frac13.$ For $n\geq2,$ the probability that the cricket land on each leaf after $n$ hops is $\frac13$ the sum of the probability the cricket land on other leaves after $n-1$ hops. So, we have \begin{align*} A(n) &= \frac13 \cdot [B(n-1) + C(n-1) + D(n-1)], \\ B(n) &= \frac13 \cdot [A(n-1) + C(n-1) + D(n-1)], \\ C(n) &= \frac13 \cdot [A(n-1) + B(n-1) + D(n-1)], \\ D(n) &= \frac13 \cdot [A(n-1) + B(n-1) + C(n-1)]. \end{align*} It follows that $A(n) = B(n-1) = C(n-1) = D(n-1).$

We construct the following table: \[\begin{array}{c|cccc} & & & & \\ [-2ex] n & A(n) & B(n) & C(n) & D(n) \\ [1ex] \hline & & & & \\ [-1ex] 1 & 0 & \frac13 & \frac13 & \frac13 \\ & & & & \\ 2 & \frac13 & \frac29 & \frac29 & \frac29 \\ & & & & \\ 3 & \frac29 & \frac{7}{27} & \frac{7}{27} & \frac{7}{27} \\ & & & & \\ 4 & \frac{7}{27} & \frac{20}{81} & \frac{20}{81} & \frac{20}{81} \\ [1ex] \end{array}\] Therefore, the answer is $A(4)=\boxed{\textbf{(E) }\frac{7}{27}}$.

~isabelchen

Solution 6 (Generating Function)

Assign the leaves to $0, 1, 2,$ and $3$ modulo $4,$ and let $0$ be the starting leaf. We then use generating functions with relation to the change of leaves. For example, from $3$ to $1$ would be a change of $2,$ and from $1$ to $2$ would be a change of $1.$ This generating function is equal to $(x+x^2+x^3)^4.$ It is clear that we want the coefficients in the form of $x^{4n},$ where $n$ is a positive integer. One application of roots of unity filter gives us a successful case count of $\frac{81+1+1+1}{4} = 21.$

Therefore, the answer is $\frac{21}{3^4}=\boxed{\textbf{(E) }\frac{7}{27}}.$

~sigma

Solution 7 (Also Generating Functions)

Let the leaves be $(0,0), (0,1), (1,0),$ and $(1,1)$ on the coordinate plane, with the cricket starting at $(0,0)$. Then we write a generating function. We denote $x$ a change in the x-value of the cricket, and similarly for $y$. Then our generating function is $(x+y+xy)^4,$ and we wish to compute the number of terms in which the exponents of both x and y are even. To do this, we first square to get $(x^2 + y^2 + x^2y^2 + 2xy + 2x^2y + 2xy^2)^2$. Note that every term squared will give even powers for x and y, so that gives us $3 + 4\cdot3 = 15.$ Then every combination of $x^2, y^2,$ and $x^2y^2$ will also give us even powers for x and y, so that yields $6$ more terms, for a total of $21.$ Now in total there $3^4 = 81$ possible sequences, so $21/81$ gives us the answer of $\boxed{\textbf{(E) }\frac{7}{27}}.$

~littlefox_amc

Remark

This problem is a reduced version of 1985 AIME Problem 12, changing $7$ steps into $4$ steps.

This problem is also similar to 2003 AIME II Problem 13.

~isabelchen

Video Solution by Math-X (First understand the problem!!!)

https://youtu.be/oUEa7AjMF2A?si=n9aPrcW_qLqFC8IF&t=5261

~Math-X

Video Solution(🚀Under 2 min🚀 Easy logic with all paths color-coded ✨)

https://youtu.be/YiI9szmMWX4

~Education, the Study of Everything

Video Solution

https://youtu.be/GNFG4cmYDgw

Please like and subscribe!

Video Solution by OmegaLearn

https://youtu.be/kE15Sy0B2Pk?t=633

~ pi_is_3.14

Video Solution

https://www.youtube.com/watch?v=85A6av3oqRo

~Mathematical Dexterity

Video Solution

https://youtu.be/Ij9pAy6tQSg?t=2588

~Interstigation

Video Solution

https://www.youtube.com/watch?v=H1zxrkq6DKg

~David

Video Solution

https://youtu.be/0orAAUaLIO0?t=609

~STEMbreezy

Video Solution

https://youtu.be/9SKUdTut3l4

~savannahsolver

Video Solution Using States by SpreadTheMathLove

https://www.youtube.com/watch?v=740Z355PtWs&t=777s

See Also

2022 AMC 8 (Problems • Answer Key • Resources)
Preceded by
Problem 24 		Followed by
Last Problem
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AJHSME/AMC 8 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2022_AMC_8_Problems/Problem_25&oldid=219999"