Difference between revisions of "Kimberling’s point X(24)"
(→Kimberling's point X(24)) |
(→Theorem 3) |
||
| (8 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
Kimberling defined point X(24) as perspector of <math>\triangle ABC</math> and Orthic Triangle of the Orthic Triangle of <math>\triangle ABC</math>. | Kimberling defined point X(24) as perspector of <math>\triangle ABC</math> and Orthic Triangle of the Orthic Triangle of <math>\triangle ABC</math>. | ||
| − | + | ==Theorem 1== | |
Denote <math>T_0</math> obtuse or acute <math>\triangle ABC.</math> Let <math>T_0</math> be the base triangle, <math>T_1 = \triangle DEF</math> be Orthic triangle of <math>T_0, T_2 = \triangle UVW</math> be Orthic Triangle of <math>T_1</math>. Let <math>O</math> and <math>H</math> be the circumcenter and orthocenter of <math>T_0.</math> | Denote <math>T_0</math> obtuse or acute <math>\triangle ABC.</math> Let <math>T_0</math> be the base triangle, <math>T_1 = \triangle DEF</math> be Orthic triangle of <math>T_0, T_2 = \triangle UVW</math> be Orthic Triangle of <math>T_1</math>. Let <math>O</math> and <math>H</math> be the circumcenter and orthocenter of <math>T_0.</math> | ||
| Line 59: | Line 59: | ||
<cmath>\angle BSH = 90 ^\circ – \angle QSB = 90 ^\circ – \angle CSS' =\angle CSH.</cmath> | <cmath>\angle BSH = 90 ^\circ – \angle QSB = 90 ^\circ – \angle CSS' =\angle CSH.</cmath> | ||
| − | <i><b>Theorem 2</b></i> | + | ==Theorem 2== |
| + | [[File:2016 USAMO 3e.png|400px|right]] | ||
| + | Let <math>T_0 = \triangle ABC</math> be the base triangle, <math>T_1 = \triangle DEF</math> be orthic triangle of <math>T_0, T_2 = \triangle KLM</math> be Kosnita triangle of <math>T_0.</math> Then <math>\triangle T_1</math> and <math>\triangle T_2</math> are homothetic, the point <math>P,</math> center of this homothety lies on Euler line of <math>T_0,</math> the ratio of the homothety is <math>k = \frac {\vec PH}{\vec OP} = 4 \cos A \cos B \cos C.</math> | ||
| + | We recall that vertex of Kosnita triangle are: <math>K</math> is the circumcenter of <math>\triangle OBC, L</math> is the circumcenter of <math>\triangle OAB, M</math> is the circumcenter of <math>\triangle OAC,</math> where <math>O</math> is circumcenter of <math>T_0.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Let <math>H</math> be orthocenter of <math>T_0, Q</math> be the center of Nine-point circle of <math>T_0, HQO</math> is the Euler line of <math>T_0.</math> | ||
| + | Well known that <math>EF</math> is antiparallel <math>BC</math> with respect <math>\angle A.</math> | ||
| + | |||
| + | <math>LM</math> is the bisector of <math>AO,</math> therefore <math>LM</math> is antiparallel <math>BC</math> with respect <math>\angle A</math> | ||
| + | <cmath>\implies LM||EF.</cmath> | ||
| + | Similarly, <math>DE||KL, DF||KM \implies \triangle DEF</math> and <math>\triangle KLM</math> are homothetic. | ||
| + | |||
| + | Let <math>P</math> be the center of homothety. | ||
| + | |||
| + | <math>H</math> is <math>D</math>-excenter of <math>\triangle DEF, O</math> is <math>K</math>-excenter of <math>\triangle KLM \implies</math> | ||
| + | <math>P \in HO.</math> | ||
| + | |||
| + | Denote <math>a = BC, \alpha = \angle A, \beta = \angle B, \gamma = \angle C, R</math> circumradius <math>\triangle ABC.</math> | ||
| + | <math>\angle EHF = 180^\circ - \alpha, EF = BC |\cos \alpha| = 2R \sin \alpha |\cos \alpha|.</math> | ||
| + | <cmath>LM = \frac {R}{2} (\tan \beta + \tan \gamma) = \frac {R \sin (\beta + \gamma)}{2 \cos \beta \cdot \cos \gamma} \implies</cmath> | ||
| + | <cmath>k = \frac {DE}{KL} = 4\cos \alpha \cdot \cos \beta \cdot \cos \gamma \implies</cmath> | ||
| + | <math>\frac {\vec {PH}}{\vec {OP}}= 4 \cos A \cos B \cos C \implies P</math> is the point <math>X(24).</math> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | ==Theorem 3== | ||
| + | [[File:X24 as Exeter.png|450px|right]] | ||
| + | Let <math>\triangle ABC</math> be the reference triangle (other than a right triangle). Let the altitudes through the vertices <math>A, B, C</math> meet the circumcircle <math>\Omega</math> of triangle <math>ABC</math> at <math>A_0, B_0,</math> and <math>C_0,</math> respectively. Let <math>A'B'C'</math> be the triangle formed by the tangents at <math>A, B,</math> and <math>C</math> to <math>\Omega.</math> (Let <math>A'</math> be the vertex opposite to the side formed by the tangent at the vertex A). Prove that the lines through <math>A_0A', B_0B',</math> and <math>C_0C'</math> are concurrent, the point of concurrence <math>X_{24}</math> lies on Euler line of triangle <math>ABC, X_{24} = O + \frac {2}{J^2 + 1} (H – O), J = \frac {|OH|}{R}.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | At first one can prove that lines <math>A_0A', B_0B',</math> and <math>C_0C'</math> are concurrent. This follows from the fact that lines <math>AA_0, BB_0,</math> and <math>CC_0</math> are concurrent at point <math>H</math> and <i><b>Mapping theorem</b></i> (see Exeter point <math>X_{22}).</math> | ||
| + | |||
| + | Let <math>A_1, B_1,</math> and <math>C_1</math> be the midpoints of <math>BC, AC,</math> and <math>AB,</math> respectively. | ||
| + | |||
| + | Let <math>A_2, B_2,</math> and <math>C_2</math> be the midpoints of <math>AH, BH,</math> and <math>CH,</math> respectively. | ||
| + | |||
| + | Let <math>A_3, B_3,</math> and <math>C_3</math> be the foots of altitudes from <math>A, B,</math> and <math>C,</math> respectively. | ||
| + | |||
| + | The points <math>A, A_2, H,</math> and <math>A_3</math> are collinear. Similarly the points <math>B, B_2, H, B_3</math> and <math>C, C_2, H, C_3</math> are collinear. | ||
| + | |||
| + | Denote <math>I_{\Omega}</math> the inversion with respect <math>\Omega.</math> It is evident that <math>I_{\Omega}(A') = A_1, I_{\Omega}(B') = B_1, I_{\Omega}(C') = C_1, I_{\Omega}(A_0) = A_0, I_{\Omega}(B_0) = B_0, I_{\Omega}(C_0) = C_0.</math> | ||
| + | |||
| + | Denote <math>\omega_A = I_{\Omega}(A'A_0), \omega_B = I_{\Omega}(B'B_0) \omega_C = I_{\Omega}(C'C_0) \implies</math> | ||
| + | <cmath>A_0 \in \omega_A, A_1 \in \omega_A, O \in \omega_A, B_0 \in \omega_B, B_1 \in \omega_B, O \in \omega_B \implies\ O = \omega_A \cap \omega_B \cap \omega_C.</cmath> | ||
| − | + | It is known that <math>A_2O = HA_1 = A_0A_1, A_2O || HA_1 \implies \angle OA_2A_0 = \angle A_1A_0A_2, OA_1 ||A_0A_2 \implies A_2 \in \omega_A.</math> | |
| − | We | + | |
| + | Similarly, <math>B_2 \in \omega_B, C_2 \in \omega_C.</math> | ||
| + | |||
| + | We use <i><b>Claim</b></i> and get that the power of point <math>H</math> with respect each circle <math>\omega_X</math> is | ||
| + | <cmath>HA_2 \cdot HA_0 = HB_2 \cdot HB_0 = HC_2 \cdot HC_0 = \frac {R^2 \cdot (1-J^2)} {2}.</cmath> | ||
| + | <math>H = AA_0 \cap BB_0 \cap CC_0 \implies H</math> lies on common radical axis of <math>\omega_A, \omega_B,</math> and <math>\omega_C.</math> | ||
| + | |||
| + | Therefore second crosspoint of these circles point <math>E</math> lies on line <math>OH</math> which is the Euler line of <math>\triangle ABC \implies</math> <math>X_{24} = I_{\Omega}(E)</math> lies on the same Euler line as desired. | ||
| + | |||
| + | Last we will find the length of <math>OX_{24}.</math> | ||
| + | <cmath>OH \cdot HE = \frac {R^2 \cdot (1–J^2)} {2}.</cmath> | ||
| + | <cmath>OE \cdot OX_{24} = (OH + HE)\cdot OX_{24} = R^2.</cmath> | ||
| + | <math>\frac {OX_{24}}{OH} = \frac {R^2}{OH^2 + OH \cdot HE} = \frac {1}{J^2 + \frac {1– J^2} {2}} = | ||
| + | \frac {2}{1+J^2},</math> as desired. | ||
| + | |||
| + | <i><b>Claim</b></i> | ||
| + | [[File:AH HF.png|400px|right]] | ||
| + | Let <math>AD, BE,</math> and <math>CF</math> be the heights of <math>\triangle ABC, H = AD \cap BE \cap CF.</math> | ||
| + | |||
| + | Prove that <math>AH \cdot HD = \frac {R^2 (1 – J^2)}{2},</math> | ||
| + | |||
| + | where <math>R</math> and <math>O</math> are circumradius and circumcenter of <math>\triangle ABC, J = \frac {OH}{R}.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | It is known that <math>\triangle ABC \sim \triangle AEF.</math> | ||
| + | <math>k = \frac {AF} {AC} = \cos A \implies AH = 2 R k = 2 R \cos A.</math> | ||
| + | |||
| + | Similarly <math>BH = 2 R \cos B, DH = BH \sin \angle CBE = BH \cos C = 2R \cos B \cos C.</math> | ||
| + | |||
| + | Therefore <math>AH \cdot HD = 4R^2 \cos A \cos B \cos C.</math> | ||
| + | |||
| + | <cmath>J^2 = \frac {HO^2}{R^2} = 1 – 8 \cos A \cos B \cos C \ \implies AH \cdot HD = \frac {R^2 (1 – J^2)}{2}.</cmath> | ||
| + | |||
'''vladimir.shelomovskii@gmail.com, vvsss''' | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
Latest revision as of 14:34, 25 November 2022
Kimberling's point X(24)
Kimberling defined point X(24) as perspector of ![]() and Orthic Triangle of the Orthic Triangle of
and Orthic Triangle of the Orthic Triangle of ![]() .
.
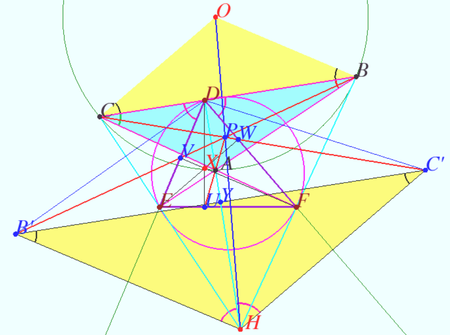
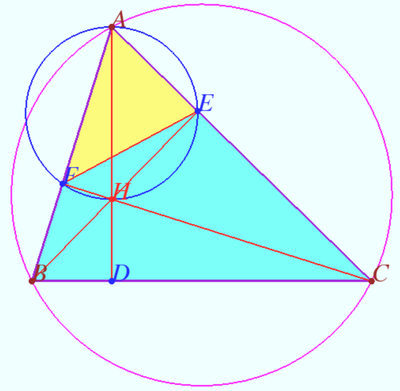
Theorem 1
Denote ![]() obtuse or acute
obtuse or acute ![]() Let
Let ![]() be the base triangle,
be the base triangle, ![]() be Orthic triangle of
be Orthic triangle of ![]() be Orthic Triangle of
be Orthic Triangle of ![]() . Let
. Let ![]() and
and ![]() be the circumcenter and orthocenter of
be the circumcenter and orthocenter of ![]()
Then ![]() and
and ![]() are homothetic, the point
are homothetic, the point ![]() center of this homothety lies on Euler line
center of this homothety lies on Euler line ![]() of
of ![]()
The ratio of the homothety is ![]()
Proof
WLOG, we use case ![]()
Let ![]() be reflection
be reflection ![]() in
in ![]() In accordance with Claim,
In accordance with Claim, ![]() and
and ![]() are collinear.
are collinear.
Similarly, ![]() and
and ![]() were
were ![]() is reflection
is reflection ![]() in
in ![]() are collinear.
are collinear.
Denote ![]()
![]()
![]()
![]()
![]() and
and ![]() are concurrent at point
are concurrent at point ![]()
In accordance with Claim, ![]() points
points ![]() and
and ![]() are isogonal conjugate with respect
are isogonal conjugate with respect ![]()
![]()
![]()
![]()
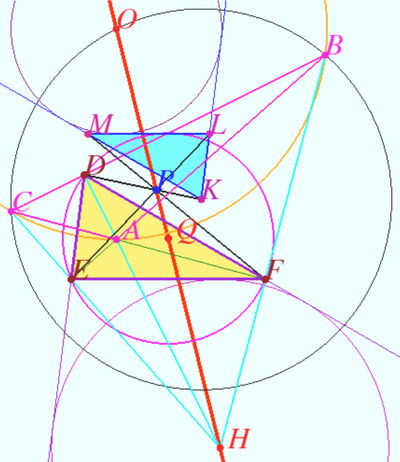
Claim
Let ![]() be an acute triangle, and let
be an acute triangle, and let ![]() and
and ![]() denote its altitudes. Lines
denote its altitudes. Lines ![]() and
and ![]() meet at
meet at ![]() Prove that
Prove that ![]()
Proof
Let ![]() be the circle
be the circle ![]() centered at
centered at ![]() is midpoint
is midpoint ![]()
Let ![]() meet
meet ![]() at
at ![]() Let
Let ![]() be the circle centered at
be the circle centered at ![]() with radius
with radius ![]()
Let ![]() be the circle with diameter
be the circle with diameter ![]()
Well known that ![]() is the polar of point
is the polar of point ![]() so
so ![]()
![]()
Let ![]() be inversion with respect
be inversion with respect ![]()
Denote ![]()
![]()
![]()
![]()
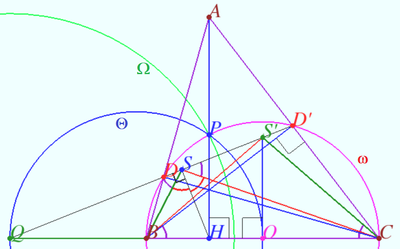
Theorem 2
Let ![]() be the base triangle,
be the base triangle, ![]() be orthic triangle of
be orthic triangle of ![]() be Kosnita triangle of
be Kosnita triangle of ![]() Then
Then ![]() and
and ![]() are homothetic, the point
are homothetic, the point ![]() center of this homothety lies on Euler line of
center of this homothety lies on Euler line of ![]() the ratio of the homothety is
the ratio of the homothety is ![]() We recall that vertex of Kosnita triangle are:
We recall that vertex of Kosnita triangle are: ![]() is the circumcenter of
is the circumcenter of ![]() is the circumcenter of
is the circumcenter of ![]() is the circumcenter of
is the circumcenter of ![]() where
where ![]() is circumcenter of
is circumcenter of ![]()
Proof
Let ![]() be orthocenter of
be orthocenter of ![]() be the center of Nine-point circle of
be the center of Nine-point circle of ![]() is the Euler line of
is the Euler line of ![]() Well known that
Well known that ![]() is antiparallel
is antiparallel ![]() with respect
with respect ![]()
![]() is the bisector of
is the bisector of ![]() therefore
therefore ![]() is antiparallel
is antiparallel ![]() with respect
with respect ![]()
![]() Similarly,
Similarly, ![]() and
and ![]() are homothetic.
are homothetic.
Let ![]() be the center of homothety.
be the center of homothety.
![]() is
is ![]() -excenter of
-excenter of ![]() is
is ![]() -excenter of
-excenter of ![]()
![]()
Denote ![]() circumradius
circumradius ![]()
![]()
![]()
![]()
![]() is the point
is the point ![]()
vladimir.shelomovskii@gmail.com, vvsss
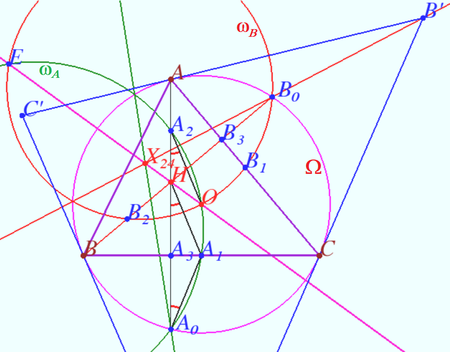
Theorem 3
Let ![]() be the reference triangle (other than a right triangle). Let the altitudes through the vertices
be the reference triangle (other than a right triangle). Let the altitudes through the vertices ![]() meet the circumcircle
meet the circumcircle ![]() of triangle
of triangle ![]() at
at ![]() and
and ![]() respectively. Let
respectively. Let ![]() be the triangle formed by the tangents at
be the triangle formed by the tangents at ![]() and
and ![]() to
to ![]() (Let
(Let ![]() be the vertex opposite to the side formed by the tangent at the vertex A). Prove that the lines through
be the vertex opposite to the side formed by the tangent at the vertex A). Prove that the lines through ![]() and
and ![]() are concurrent, the point of concurrence
are concurrent, the point of concurrence ![]() lies on Euler line of triangle
lies on Euler line of triangle ![]()
Proof
At first one can prove that lines ![]() and
and ![]() are concurrent. This follows from the fact that lines
are concurrent. This follows from the fact that lines ![]() and
and ![]() are concurrent at point
are concurrent at point ![]() and Mapping theorem (see Exeter point
and Mapping theorem (see Exeter point ![]()
Let ![]() and
and ![]() be the midpoints of
be the midpoints of ![]() and
and ![]() respectively.
respectively.
Let ![]() and
and ![]() be the midpoints of
be the midpoints of ![]() and
and ![]() respectively.
respectively.
Let ![]() and
and ![]() be the foots of altitudes from
be the foots of altitudes from ![]() and
and ![]() respectively.
respectively.
The points ![]() and
and ![]() are collinear. Similarly the points
are collinear. Similarly the points ![]() and
and ![]() are collinear.
are collinear.
Denote ![]() the inversion with respect
the inversion with respect ![]() It is evident that
It is evident that ![]()
Denote ![]()
![]()
It is known that ![]()
Similarly, ![]()
We use Claim and get that the power of point ![]() with respect each circle
with respect each circle ![]() is
is
![]()
![]() lies on common radical axis of
lies on common radical axis of ![]() and
and ![]()
Therefore second crosspoint of these circles point ![]() lies on line
lies on line ![]() which is the Euler line of
which is the Euler line of ![]()
![]() lies on the same Euler line as desired.
lies on the same Euler line as desired.
Last we will find the length of ![]()
![]()
![]()
![]() as desired.
as desired.
Claim
Let ![]() and
and ![]() be the heights of
be the heights of ![]()
Prove that ![]()
where ![]() and
and ![]() are circumradius and circumcenter of
are circumradius and circumcenter of ![]()
Proof
It is known that ![]()
![]()
Similarly ![]()
Therefore ![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss