Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2005 AMC 12A Problems/Problem 7"

(→‎Solution)
(Added image)
 
(3 intermediate revisions by 2 users not shown)
Line 1: Line 1:
 
== Problem ==
 
== Problem ==
 
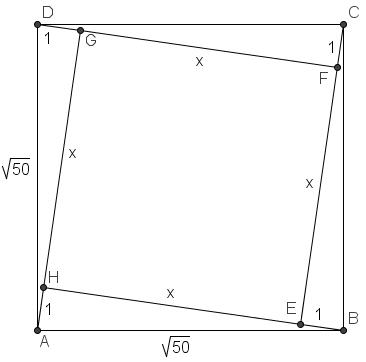
[[Square]] <math>EFGH</math> is inside the square <math>ABCD</math> so that each side of <math>EFGH</math> can be extended to pass through a vertex of <math>ABCD</math>. Square <math>ABCD</math> has side length <math>\sqrt {50}</math> and <math>BE = 1</math>. What is the area of the inner square <math>EFGH</math>?
 
[[Square]] <math>EFGH</math> is inside the square <math>ABCD</math> so that each side of <math>EFGH</math> can be extended to pass through a vertex of <math>ABCD</math>. Square <math>ABCD</math> has side length <math>\sqrt {50}</math> and <math>BE = 1</math>. What is the area of the inner square <math>EFGH</math>?
 +
 +
<asy>
 +
unitsize(4cm);
 +
defaultpen(linewidth(.8pt)+fontsize(10pt));
 +
pair D=(0,0), C=(1,0), B=(1,1), A=(0,1);
 +
pair F=intersectionpoints(Circle(D,2/sqrt(5)),Circle(A,1))[0];
 +
pair G=foot(A,D,F), H=foot(B,A,G), E=foot(C,B,H);
 +
draw(A--B--C--D--cycle);
 +
draw(D--F);
 +
draw(C--E);
 +
draw(B--H);
 +
draw(A--G);
 +
label("$A$",A,NW);
 +
label("$B$",B,NE);
 +
label("$C$",C,SE);
 +
label("$D$",D,SW);
 +
label("$E$",E,NNW);
 +
label("$F$",F,ENE);
 +
label("$G$",G,SSE);
 +
label("$H$",H,WSW);
 +
</asy>
  
 
<math>
 
<math>
 
(\mathrm {A}) \ 25 \qquad (\mathrm {B}) \ 32 \qquad (\mathrm {C})\ 36 \qquad (\mathrm {D}) \ 40 \qquad (\mathrm {E})\ 42
 
(\mathrm {A}) \ 25 \qquad (\mathrm {B}) \ 32 \qquad (\mathrm {C})\ 36 \qquad (\mathrm {D}) \ 40 \qquad (\mathrm {E})\ 42
 
</math>
 
</math>
 +
 
== Solution ==
 
== Solution ==
 
[[Image:2005_12A_AMC-7b.png]]
 
[[Image:2005_12A_AMC-7b.png]]
Line 13: Line 35:
  
 
Notice the [[right triangle]] (in blue) with legs <math>1, x+1</math> and [[hypotenuse]] <math>\sqrt{50}</math>. By the [[Pythagorean Theorem]], we have <math>1^2 + (x+1)^2 = (\sqrt{50})^2 \Longrightarrow (x+1)^2 = 49 \Longrightarrow x = 6</math>. Thus, <math>[EFGH] = x^2 = 36\ \mathrm{(C)}</math>
 
Notice the [[right triangle]] (in blue) with legs <math>1, x+1</math> and [[hypotenuse]] <math>\sqrt{50}</math>. By the [[Pythagorean Theorem]], we have <math>1^2 + (x+1)^2 = (\sqrt{50})^2 \Longrightarrow (x+1)^2 = 49 \Longrightarrow x = 6</math>. Thus, <math>[EFGH] = x^2 = 36\ \mathrm{(C)}</math>
−
== Solution ==
 
−
You can also notice that the four triangles <math>\triangle ABH,\triangle BCE,\triangle CDF,\triangle DAG</math> are congruent because the right angles of square <math>ABCD</math> cause them to be similar, and the hypotenuse of the triangles are the same because they are the sides of the square. Then you have <math>[ABCD]-4*7=50-28=22\Rightarrow\boxed{C}.</math>
 
−
Solution by wxl18
 
−
 
 
== See also ==
 
== See also ==
 
{{AMC12 box|year=2005|num-b=6|num-a=8|ab=A}}
 
{{AMC12 box|year=2005|num-b=6|num-a=8|ab=A}}

Latest revision as of 10:15, 19 July 2024

Problem

Square $EFGH$ is inside the square $ABCD$ so that each side of $EFGH$ can be extended to pass through a vertex of $ABCD$. Square $ABCD$ has side length $\sqrt {50}$ and $BE = 1$. What is the area of the inner square $EFGH$?

[asy] unitsize(4cm); defaultpen(linewidth(.8pt)+fontsize(10pt)); pair D=(0,0), C=(1,0), B=(1,1), A=(0,1); pair F=intersectionpoints(Circle(D,2/sqrt(5)),Circle(A,1))[0]; pair G=foot(A,D,F), H=foot(B,A,G), E=foot(C,B,H); draw(A--B--C--D--cycle); draw(D--F); draw(C--E); draw(B--H); draw(A--G); label("$A$",A,NW); label("$B$",B,NE); label("$C$",C,SE); label("$D$",D,SW); label("$E$",E,NNW); label("$F$",F,ENE); label("$G$",G,SSE); label("$H$",H,WSW); [/asy]

$(\mathrm {A}) \ 25 \qquad (\mathrm {B}) \ 32 \qquad (\mathrm {C})\ 36 \qquad (\mathrm {D}) \ 40 \qquad (\mathrm {E})\ 42$

Solution

2005 12A AMC-7b.png

Arguable the hardest part of this question is to visualize the diagram. Since each side of $EFGH$ can be extended to pass through a vertex of $ABCD$, we realize that $EFGH$ must be tilted in such a fashion. Let a side of $EFGH$ be $x$.

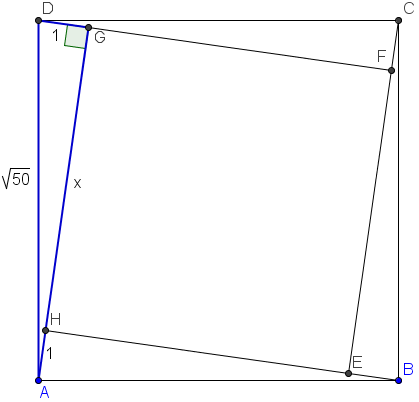
2005 12A AMC-7.png

Notice the right triangle (in blue) with legs $1, x+1$ and hypotenuse $\sqrt{50}$. By the Pythagorean Theorem, we have $1^2 + (x+1)^2 = (\sqrt{50})^2 \Longrightarrow (x+1)^2 = 49 \Longrightarrow x = 6$. Thus, $[EFGH] = x^2 = 36\ \mathrm{(C)}$

See also

2005 AMC 12A (Problems • Answer Key • Resources)
Preceded by
Problem 6 		Followed by
Problem 8
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2005_AMC_12A_Problems/Problem_7&oldid=223126"