Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2017 IMO Problems/Problem 4"

(→‎Solution)
 
(16 intermediate revisions by 2 users not shown)
Line 1: Line 1:
 +
==Problem==
 +
 
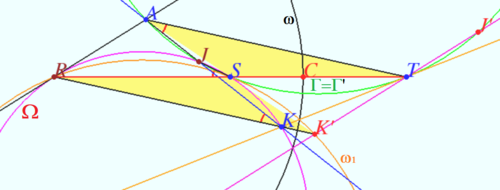
Let <math>R</math> and <math>S</math> be different points on a circle <math>\Omega</math> such that <math>RS</math> is not a diameter. Let <math>\ell</math> be the tangent line to <math>\Omega</math> at <math>R</math>. Point <math>T</math> is such that <math>S</math> is the midpoint of the line segment <math>RT</math>. Point <math>J</math> is chosen on the shorter arc <math>RS</math> of <math>\Omega</math> so that the circumcircle <math>\Gamma</math> of triangle <math>JST</math> intersects <math>\ell</math> at two distinct points. Let <math>A</math> be the common point of <math>\Gamma</math> and <math>\ell</math> that is closer to <math>R</math>. Line <math>AJ</math> meets <math>\Omega</math> again at <math>K</math>. Prove that the line <math>KT</math> is tangent to <math>\Gamma</math>.
 
Let <math>R</math> and <math>S</math> be different points on a circle <math>\Omega</math> such that <math>RS</math> is not a diameter. Let <math>\ell</math> be the tangent line to <math>\Omega</math> at <math>R</math>. Point <math>T</math> is such that <math>S</math> is the midpoint of the line segment <math>RT</math>. Point <math>J</math> is chosen on the shorter arc <math>RS</math> of <math>\Omega</math> so that the circumcircle <math>\Gamma</math> of triangle <math>JST</math> intersects <math>\ell</math> at two distinct points. Let <math>A</math> be the common point of <math>\Gamma</math> and <math>\ell</math> that is closer to <math>R</math>. Line <math>AJ</math> meets <math>\Omega</math> again at <math>K</math>. Prove that the line <math>KT</math> is tangent to <math>\Gamma</math>.
  
Line 5: Line 7:
 
We construct inversion which maps <math>KT</math> into the circle <math>\omega_1</math> and  <math>\Gamma</math> into  <math>\Gamma.</math> Than we prove that <math>\omega_1</math> is tangent to <math>\Gamma.</math>
 
We construct inversion which maps <math>KT</math> into the circle <math>\omega_1</math> and  <math>\Gamma</math> into  <math>\Gamma.</math> Than we prove that <math>\omega_1</math> is tangent to <math>\Gamma.</math>
  
−
Quadrungle <math>RJSK</math> is cyclic <math>\implies \angle RSJ = \angle RKJ.</math>
+
Quadrangle <math>RJSK</math> is cyclic <math>\implies \angle RSJ = \angle RKJ.</math>
−
Quadrungle <math>AJST</math> is cyclic <math>\implies \angle RSJ = \angle TAJ \implies AT||RK.</math>
+
 
 +
Quadrangle <math>AJST</math> is cyclic <math>\implies \angle RSJ = \angle TAJ \implies AT||RK.</math>
  
 
We construct circle <math>\omega</math> centered at <math>R</math> which maps  <math>\Gamma</math> into  <math>\Gamma.</math>
 
We construct circle <math>\omega</math> centered at <math>R</math> which maps  <math>\Gamma</math> into  <math>\Gamma.</math>
  
−
Let <math>C = \omega \cap RT \implies RC^2 = RS \cdot RT.</math> Inversion with respect <math>\omega</math> swap <math>T</math> and <math>S \implies  \Gamma</math> maps into  <math>\Gamma (\Gamma = \Gamma').</math>
+
Let <math>C = \omega \cap RT \implies RC^2 = RS \cdot RT.</math> Inversion with respect to <math>\omega</math> swap <math>T</math> and <math>S \implies  \Gamma</math> maps into  <math>\Gamma (\Gamma = \Gamma').</math>
  
 
Let <math>O</math> be the center of <math>\Gamma.</math>
 
Let <math>O</math> be the center of <math>\Gamma.</math>
  
−
Inversion with respect <math>\omega</math>  maps <math>K</math> into <math>K'</math>.
+
Inversion with respect to <math>\omega</math>  maps <math>K</math> into <math>K'</math>.
 
<math>K</math> belong <math>KT \implies</math> circle  <math>K'SR = \omega_1</math> is the image of <math>KT</math>. Let <math>Q</math> be the center of <math>\omega_1.</math>
 
<math>K</math> belong <math>KT \implies</math> circle  <math>K'SR = \omega_1</math> is the image of <math>KT</math>. Let <math>Q</math> be the center of <math>\omega_1.</math>
  
 
<math>K'T</math> is the image of <math>\Omega</math> at this inversion, <math>l = AR</math> is tangent line to <math>\Omega</math> at <math>R,</math> so <math>K'T||AR.</math>  
 
<math>K'T</math> is the image of <math>\Omega</math> at this inversion, <math>l = AR</math> is tangent line to <math>\Omega</math> at <math>R,</math> so <math>K'T||AR.</math>  
 
   
 
   
−
<math>K'</math> is image K at this inversion <math>\implies K \in RK' \implies RK'||AT \implies ARK'T</math> is parallelogramm.
+
<math>K'</math> is image K at this inversion <math>\implies K \in RK' \implies RK'||AT \implies ARK'T</math> is parallelogram.
 
   
 
   
 
<math>S</math> is the midpoint of <math>RT \implies S</math> is the center of symmetry of <math>ATK'R \implies</math>
 
<math>S</math> is the midpoint of <math>RT \implies S</math> is the center of symmetry of <math>ATK'R \implies</math>
 
<math>\triangle RSK'</math> is symmetrical to <math>\triangle TSA</math> with respect to <math>S \implies</math>  
 
<math>\triangle RSK'</math> is symmetrical to <math>\triangle TSA</math> with respect to <math>S \implies</math>  
 
<math>\omega_1</math>  is symmetrical to <math>\Gamma</math> with respect to <math>S \implies</math>
 
<math>\omega_1</math>  is symmetrical to <math>\Gamma</math> with respect to <math>S \implies</math>
−
<math>O</math> is symmetrycal <math>Q</math> with respect to <math>S, S</math> lies on <math>\Gamma</math> and on <math>|omega_1 \implies</math>
+
<math>O</math> is symmetrycal <math>Q</math> with respect to <math>S.</math>
−
<math>\Gamma</math> is tangent <math>\omega_1 \implies S\Gamma</math> is tangent <math>TK.</math>
+
 
 +
<math>S</math> lies on <math>\Gamma</math> and on <math>\omega_1 \implies \Gamma</math> is tangent to <math>\omega_1 \implies</math> line <math>KT</math> is tangent to <math>\Gamma.</math>
 +
 
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
 
 +
==Solution 2==
 +
[[File:2017 IMO 4a.png|500px|right]]
 +
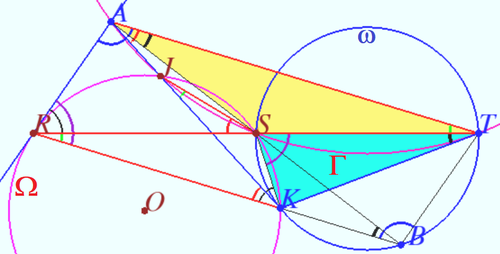
We use the tangent-chord theorem: the angle formed between a chord and a tangent line to a circle is equal to the inscribed angle on the other side of the chord.
 +
 
 +
Quadrangle <math>RJSK</math> is cyclic <math>\implies \angle RSJ = \angle RKJ.</math>
 +
 
 +
Quadrangle <math>AJST</math> is cyclic <math>\implies \angle RSJ = \angle TAJ</math> <cmath>\implies AT||RK.</cmath>
 +
 
 +
(One can use Reim’s theorem – it is shorter way.)
 +
 
 +
Let <math>B</math> be symmetric to <math>A</math> with respect to <math>S \implies</math>
 +
<math>ATBR</math> is parallelogram.
 +
<cmath>\angle KST = \angle SRK + \angle SKR = \angle KRA</cmath>
 +
<math>\angle RBT = \angle RAT \implies \angle KST + \angle KBT = 180^\circ</math>
 +
<math>\implies SKBT</math> is cyclic.
 +
<cmath>\angle SBK = \angle STK  = \angle SAT \implies </cmath>
 +
 
 +
Inscribed angle of <math>\Gamma (\angle SAT)</math> is equal to angle between <math>KT</math> and chord <math>ST \implies</math>
 +
 
 +
<math>KT</math> is tangent to <math>\Gamma</math> by the inverse of tangent-chord theorem.
 +
 
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
 
 +
==See Also==
 +
 
 +
{{IMO box|year=2017|num-b=3|num-a=5}}

Latest revision as of 00:41, 19 November 2023

Problem

Let $R$ and $S$ be different points on a circle $\Omega$ such that $RS$ is not a diameter. Let $\ell$ be the tangent line to $\Omega$ at $R$. Point $T$ is such that $S$ is the midpoint of the line segment $RT$. Point $J$ is chosen on the shorter arc $RS$ of $\Omega$ so that the circumcircle $\Gamma$ of triangle $JST$ intersects $\ell$ at two distinct points. Let $A$ be the common point of $\Gamma$ and $\ell$ that is closer to $R$. Line $AJ$ meets $\Omega$ again at $K$. Prove that the line $KT$ is tangent to $\Gamma$.

Solution

2017 IMO 4.png

We construct inversion which maps $KT$ into the circle $\omega_1$ and $\Gamma$ into $\Gamma.$ Than we prove that $\omega_1$ is tangent to $\Gamma.$

Quadrangle $RJSK$ is cyclic $\implies \angle RSJ = \angle RKJ.$

Quadrangle $AJST$ is cyclic $\implies \angle RSJ = \angle TAJ \implies AT||RK.$

We construct circle $\omega$ centered at $R$ which maps $\Gamma$ into $\Gamma.$

Let $C = \omega \cap RT \implies RC^2 = RS \cdot RT.$ Inversion with respect to $\omega$ swap $T$ and $S \implies \Gamma$ maps into $\Gamma (\Gamma = \Gamma').$

Let $O$ be the center of $\Gamma.$

Inversion with respect to $\omega$ maps $K$ into $K'$. $K$ belong $KT \implies$ circle $K'SR = \omega_1$ is the image of $KT$. Let $Q$ be the center of $\omega_1.$

$K'T$ is the image of $\Omega$ at this inversion, $l = AR$ is tangent line to $\Omega$ at $R,$ so $K'T||AR.$

$K'$ is image K at this inversion $\implies K \in RK' \implies RK'||AT \implies ARK'T$ is parallelogram.

$S$ is the midpoint of $RT \implies S$ is the center of symmetry of $ATK'R \implies$ $\triangle RSK'$ is symmetrical to $\triangle TSA$ with respect to $S \implies$ $\omega_1$ is symmetrical to $\Gamma$ with respect to $S \implies$ $O$ is symmetrycal $Q$ with respect to $S.$

$S$ lies on $\Gamma$ and on $\omega_1 \implies \Gamma$ is tangent to $\omega_1 \implies$ line $KT$ is tangent to $\Gamma.$

vladimir.shelomovskii@gmail.com, vvsss

Solution 2

2017 IMO 4a.png

We use the tangent-chord theorem: the angle formed between a chord and a tangent line to a circle is equal to the inscribed angle on the other side of the chord.

Quadrangle $RJSK$ is cyclic $\implies \angle RSJ = \angle RKJ.$

Quadrangle $AJST$ is cyclic $\implies \angle RSJ = \angle TAJ$ \[\implies AT||RK.\]

(One can use Reim’s theorem – it is shorter way.)

Let $B$ be symmetric to $A$ with respect to $S \implies$ $ATBR$ is parallelogram. \[\angle KST = \angle SRK + \angle SKR = \angle KRA\] $\angle RBT = \angle RAT \implies \angle KST + \angle KBT = 180^\circ$ $\implies SKBT$ is cyclic. \[\angle SBK = \angle STK = \angle SAT \implies\]

Inscribed angle of $\Gamma (\angle SAT)$ is equal to angle between $KT$ and chord $ST \implies$

$KT$ is tangent to $\Gamma$ by the inverse of tangent-chord theorem.

vladimir.shelomovskii@gmail.com, vvsss

See Also

2017 IMO (Problems) • Resources
Preceded by
Problem 3 		1 • 2 • 3 • 4 • 5 • 6 Followed by
Problem 5
All IMO Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2017_IMO_Problems/Problem_4&oldid=204579"