Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2020 AIME II Problems/Problem 4"

(→‎See Also)
m (→‎Solution)
 
(9 intermediate revisions by 3 users not shown)
Line 3: Line 3:
  
 
==Solution==
 
==Solution==
−
After sketching, it is clear a <math>90^{\circ}</math> rotation is done about <math>(x,y)</math>. Looking between <math>A</math> and <math>A'</math>, <math>x+y=18</math> and <math>x-y=24</math>. Solving gives <math>(x,y)\implies(21,-3)</math>. Thus <math>90+21-3=\boxed{108}</math>.
+
After sketching, it is clear a <math>90^{\circ}</math> rotation is done about <math>(x,y)</math>. Looking between <math>A</math> and <math>A'</math>, <math>x+y=18</math>. Thus <math>90+18=\boxed{108}</math>.
 
~mn28407
 
~mn28407
  
Line 80: Line 80:
 
~IceMatrix
 
~IceMatrix
  
−
==Solution 7==
+
==Solution 6==
−
 
+
[[File:2020 AIME II 4.png|500px|right]]
 
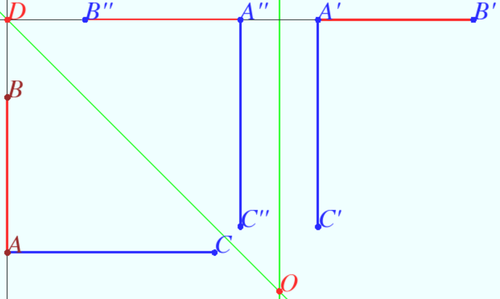
We make transformation of line <math>AB</math> into line <math>A'B'</math> using axes symmetry. Point <math>D(0,18)</math> is the crosspoint of this lines. Equation of line <math>DO</math> is  
 
We make transformation of line <math>AB</math> into line <math>A'B'</math> using axes symmetry. Point <math>D(0,18)</math> is the crosspoint of this lines. Equation of line <math>DO</math> is  
 
<cmath>x + y = 18.</cmath>
 
<cmath>x + y = 18.</cmath>
−
<math>\triangle ABC</math> maps into <math>\triangle A''B''C''</math> where <math>A''(18,18), B''(6,18), C''(18,2).</math>
+
<math>\triangle ABC</math> maps into <math>\triangle A''B''C''</math> where <cmath>A''(18,18), B''(6,18), C''(18,2).</cmath>
−
We make transform line <math>A''C''</math> into line <math>A'C'</math> using axes symmetry with respect to line <cmath>x  = \frac {A'' + A'}{2} = \frac {24 + 18}{2} = 21.</cmath>
+
 
 +
We make transform of the line <math>A''C''</math> into line <math>A'C'</math> using axes symmetry with respect to line
 +
<cmath>x  = \frac {A'' + A'}{2} = \frac {24 + 18}{2} = 21.</cmath>
 
The composition of two axial symmetries is a rotation through an angle twice as large as the angle between the axes <math>(45^o)</math> around the point of their intersection <math>O(21, – 3).</math>  
 
The composition of two axial symmetries is a rotation through an angle twice as large as the angle between the axes <math>(45^o)</math> around the point of their intersection <math>O(21, – 3).</math>  
 
<cmath>m + x + y = 90 + 21 – 3 = \boxed {108}</cmath>.
 
<cmath>m + x + y = 90 + 21 – 3 = \boxed {108}</cmath>.
  
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
 +
==Solution 7 (Matrix and Transformations)==
 +
For a matrix to rotate a figure on a coordinate plane by <math>m</math> degrees, it is written as:
 +
<math>\left[ {\begin{array}{cc}
 +
cos(m^{\circ}) & sin(m^{\circ})  \\
 +
-sin(m^{\circ}) & cos(m^{\circ})  \\
 +
\end{array} } \right]</math>
 +
 +
We can translate the whole figure so that the centre of rotation is at <math>(0,0)</math>, which is equivalent to subtracting <math>x</math> and <math>y</math> from all <math>x</math>-coordinates and the <math>y</math>-coordinates respectively of the given points.
 +
 +
We then record all the points <math>A</math>, <math>B</math>, <math>C</math> in a matrix as follows:
 +
<math>\left[ {\begin{array}{ccc}
 +
0-x & 0-x & 16-x  \\
 +
0-y & 12-y & 0-y  \\
 +
\end{array} } \right]</math>
 +
 +
and all the points <math>A'</math>, <math>B'</math>, <math>C'</math> in a matrix as follows:
 +
<math>\left[ {\begin{array}{ccc}
 +
24-x & 36-x & 24-x  \\
 +
18-y & 18-y & 2-y  \\
 +
\end{array} } \right]</math>
 +
 +
Since <math>\triangle A'B'C'</math> is a rotation around <math>(x,y)</math> of <math>\triangle ABC</math> by <math>m^{\circ}</math>, by the left multiplication rule, we can equate that:
 +
 +
<math>\left[ {\begin{array}{cc}
 +
cos(m^{\circ}) & sin(m^{\circ})  \\
 +
-sin(m^{\circ}) & cos(m^{\circ})  \\
 +
\end{array} } \right]</math>
 +
<math>\left[ {\begin{array}{ccc}
 +
0-x & 0-x & 16-x  \\
 +
0-y & 12-y & 0-y  \\
 +
\end{array} } \right]</math>
 +
<math>=</math>
 +
<math>\left[ {\begin{array}{ccc}
 +
24-x & 36-x & 24-x  \\
 +
18-y & 18-y & 2-y  \\
 +
\end{array} } \right]</math>
 +
 +
We can obtain the follow equations:
 +
<math>\begin{cases} -xcos(m^{\circ})-ysin(m^{\circ})=24-x \\ -xcos(m^{\circ})-ysin(m^{\circ})+12sin(m^{\circ})=36-x \\ xsin(m^{\circ})-ycos(m^{\circ})=24-x \end{cases}</math>
 +
 +
From the first 2 equations, we get <math>m=90</math>, substituting into the 3rd equation, we get <math>x+y=18</math>.
 +
 +
Therefore, <math>m+x+y=90+18=\boxed{108}</math>
 +
 +
~VitalsBat
 +
 +
==Solution 8==
 +
 +
It is clear that <math>\bigtriangleup CPC'</math> is a <math>45-45-90</math> right triangle so <math>m=90</math>. We use the <math>\tan</math> angle formula, <math>\tan{(a-b)}=\frac{\tan(a)-\tan(b)}{1+\tan(a)\tan(b)}</math> to find the slope of line <math>CP</math>. We know that line <math>CC'</math> has slope <math>\frac{1}{4}</math> and let <math>b=-45^{\circ}</math>, then plugging both values into the formula, we find that the slope of <math>CP</math> is <math>\frac{-3}{5}</math>. Also, <math>CC'</math> has length <math>\sqrt{34}</math>. Create a right triangle <math>KCP</math> where <math>KP</math> is parallel to the <math>x</math> axis and <math>CP</math> is the hypotenuse. Then <math>CK=3x</math> and <math>KP=5x</math> and doing Pythagorean on <math>\bigtriangleup KCP</math> gives <math>x=1</math>. Therefore, we know that <math>P</math> is a translation 3 units down and 5 units right from <math>C(16,0)</math>, from which we obtain <math>P(21,-3)</math>. Adding the three variables, we obtain <math>90+21-3=\boxed{108}</math>
  
 +
~[https://artofproblemsolving.com/wiki/index.php/User:Magnetoninja Magnetoninja]
  
 
==See Also==
 
==See Also==

Latest revision as of 12:29, 19 January 2024

Problem

Triangles $\triangle ABC$ and $\triangle A'B'C'$ lie in the coordinate plane with vertices $A(0,0)$, $B(0,12)$, $C(16,0)$, $A'(24,18)$, $B'(36,18)$, $C'(24,2)$. A rotation of $m$ degrees clockwise around the point $(x,y)$ where $0<m<180$, will transform $\triangle ABC$ to $\triangle A'B'C'$. Find $m+x+y$.

Solution

After sketching, it is clear a $90^{\circ}$ rotation is done about $(x,y)$. Looking between $A$ and $A'$, $x+y=18$. Thus $90+18=\boxed{108}$. ~mn28407

Solution 2 (Official MAA)

Because the rotation sends the vertical segment $\overline{AB}$ to the horizontal segment $\overline{A'B'}$, the angle of rotation is $90^\circ$ degrees clockwise. For any point $(x,y)$ not at the origin, the line segments from $(0,0)$ to $(x,y)$ and from $(x,y)$ to $(x-y,y+x)$ are perpendicular and are the same length. Thus a $90^\circ$ clockwise rotation around the point $(x,y)$ sends the point $A(0,0)$ to the point $(x-y,y+x) = A'(24,18)$. This has the solution $(x,y) = (21,-3)$. The requested sum is $90+21-3=108$.

Solution 3

[asy] /* Geogebra to Asymptote conversion by samrocksnature, documentation at artofproblemsolving.com/Wiki go to User:Azjps/geogebra */ real labelscalefactor = 0.5; /* changes label-to-point distance */ pen dps = linewidth(0.7) + fontsize(10); defaultpen(dps); /* default pen style */ pen dotstyle = black; /* point style */ real xmin = -8.0451801958033, xmax = 47.246151591238494, ymin = -10.271454747548662, ymax = 21.426040258770957; /* image dimensions */ pen zzttqq = rgb(0.6,0.2,0); pen qqwuqq = rgb(0,0.39215686274509803,0); pen qqffff = rgb(0,1,1); draw((16,0)--(0,0)--(0,12)--cycle, linewidth(2) + zzttqq); draw((24,2)--(24,18)--(36,18)--cycle, linewidth(2) + blue); draw((16,0)--(21,-3)--(24,2)--cycle, linewidth(2) + qqwuqq); draw((21.39134584768662,-2.3477569205223032)--(20.73910276820892,-1.9564110728356852)--(20.347756920522304,-2.608654152313382)--(21,-3)--cycle, linewidth(2) + qqffff); /* draw figures */ draw((16,0)--(0,0), linewidth(2) + zzttqq); draw((0,0)--(0,12), linewidth(2) + zzttqq); draw((0,12)--(16,0), linewidth(2) + zzttqq); draw((24,2)--(24,18), linewidth(2) + blue); draw((24,18)--(36,18), linewidth(2) + blue); draw((36,18)--(24,2), linewidth(2) + blue); draw((16,0)--(24,2), linewidth(2)); draw((16,0)--(21,-3), linewidth(2) + qqwuqq); draw((21,-3)--(24,2), linewidth(2) + qqwuqq); draw((24,2)--(16,0), linewidth(2) + qqwuqq); draw((21,-3)--(20,1), linewidth(2.8) + qqffff); /* dots and labels */ dot((0,0),linewidth(4pt) + dotstyle); label("$A$", (-0.6228029714727868,0.12704474547474198), NE * labelscalefactor); dot((0,12),dotstyle); label("$B$", (0.1301918194013232,12.354245873478124), NE * labelscalefactor); dot((16,0),dotstyle); label("$C$", (16.15822379657881,0.34218611429591583), NE * labelscalefactor); dot((24,18),dotstyle); label("$A'$", (24.154311337765787,18.342347305667463), NE * labelscalefactor); dot((24,2),dotstyle); label("$C'$", (23.186175178070503,1.95574638045472), NE * labelscalefactor); dot((36,18),dotstyle); label("$B'$", (36.13051420214449,18.342347305667463), NE * labelscalefactor); dot((21,-3),dotstyle); label("$P$", (21.35747354309052,-3.458644734878156), NE * labelscalefactor); dot((20,1),linewidth(4pt) + dotstyle); label("$D$", (20.13833911977053,1.2744653791876692), NE * labelscalefactor); clip((xmin,ymin)--(xmin,ymax)--(xmax,ymax)--(xmax,ymin)--cycle); /* end of picture */ [/asy]

We first draw a diagram with the correct Cartesian coordinates and a center of rotation $P$. Note that $PC=PC'$ because $P$ lies on the perpendicular bisector of $CC'$ (it must be equidistant from $C$ and $C'$ by properties of a rotation).

Since $AB$ is vertical while $A'B'$ is horizontal, we have that the angle of rotation must be $90^{\circ}$, and therefore $\angle P = 90^{\circ}$. Therefore, $CPC'$ is a 45-45-90 right triangle, and $CD=DP$.

We calculate $D$ to be $(20,1)$. Since we translate $4$ right and $1$ up to get from point $C$ to point $D$, we must translate $1$ right and $4$ down to get to point $P$. This gives us $P(21,-3)$. Our answer is then $90+21-3=\boxed{108}$. ~Lopkiloinm & samrocksnature

Solution 4

For the above reasons, the transformation is simply a $90^\circ$ rotation. Proceed with complex numbers on the points $C$ and $C'$. Let $(x, y)$ be the origin. Thus, $C \rightarrow (16-x)+(-y)i$ and $C' \rightarrow (24-x)+(2-y)i$. The transformation from $C'$ to $C$ is a multiplication of $i$, which yields $(16-x)+(-y)i=(y-2)+(24-x)i$. Equating the real and complex terms results in the equations $16-x=y-2$ and $-y=24-x$. Solving, $(x, y) : (21, -3) \rightarrow 90+21-3=\boxed{108}$

~beastgert

Solution 5

We know that the rotation point $P$ has to be equidistant from both $A$ and $A'$ so it has to lie on the line that is on the midpoint of the segment $AA'$ and also the line has to be perpendicular to $AA'$. Solving, we get the line is $y=\frac{-4}{3}x+25$. Doing the same for $B$ and $B'$, we get that $y=-6x+123$. Since the point $P$ of rotation must lie on both of these lines, we set them equal, solve and get: $x=21$,$y=-3$. We can also easily see that the degree of rotation is $90$ since $AB$ is initially vertical, and now it is horizontal. Also, we can just sketch this on a coordinate plane and easily realize the same. Hence, the answer is $21-3+90 = \boxed{108}$

Video Solution

https://www.youtube.com/watch?v=iJkNkSAmqhg

~North America Math Contest Go Go Go


Video Solution

https://youtu.be/atqPgGG0Ekk

~IceMatrix

Solution 6

2020 AIME II 4.png

We make transformation of line $AB$ into line $A'B'$ using axes symmetry. Point $D(0,18)$ is the crosspoint of this lines. Equation of line $DO$ is \[x + y = 18.\] $\triangle ABC$ maps into $\triangle A''B''C''$ where \[A''(18,18), B''(6,18), C''(18,2).\]

We make transform of the line $A''C''$ into line $A'C'$ using axes symmetry with respect to line \[x = \frac {A'' + A'}{2} = \frac {24 + 18}{2} = 21.\] The composition of two axial symmetries is a rotation through an angle twice as large as the angle between the axes $(45^o)$ around the point of their intersection $O(21, – 3).$ \[m + x + y = 90 + 21 – 3 = \boxed {108}\].

vladimir.shelomovskii@gmail.com, vvsss

Solution 7 (Matrix and Transformations)

For a matrix to rotate a figure on a coordinate plane by $m$ degrees, it is written as: $\left[ {\begin{array}{cc} cos(m^{\circ}) & sin(m^{\circ}) \\ -sin(m^{\circ}) & cos(m^{\circ}) \\ \end{array} } \right]$

We can translate the whole figure so that the centre of rotation is at $(0,0)$, which is equivalent to subtracting $x$ and $y$ from all $x$-coordinates and the $y$-coordinates respectively of the given points.

We then record all the points $A$, $B$, $C$ in a matrix as follows: $\left[ {\begin{array}{ccc} 0-x & 0-x & 16-x \\ 0-y & 12-y & 0-y \\ \end{array} } \right]$

and all the points $A'$, $B'$, $C'$ in a matrix as follows: $\left[ {\begin{array}{ccc} 24-x & 36-x & 24-x \\ 18-y & 18-y & 2-y \\ \end{array} } \right]$

Since $\triangle A'B'C'$ is a rotation around $(x,y)$ of $\triangle ABC$ by $m^{\circ}$, by the left multiplication rule, we can equate that:

$\left[ {\begin{array}{cc} cos(m^{\circ}) & sin(m^{\circ}) \\ -sin(m^{\circ}) & cos(m^{\circ}) \\ \end{array} } \right]$ $\left[ {\begin{array}{ccc} 0-x & 0-x & 16-x \\ 0-y & 12-y & 0-y \\ \end{array} } \right]$ $=$ $\left[ {\begin{array}{ccc} 24-x & 36-x & 24-x \\ 18-y & 18-y & 2-y \\ \end{array} } \right]$

We can obtain the follow equations: $\begin{cases} -xcos(m^{\circ})-ysin(m^{\circ})=24-x \\ -xcos(m^{\circ})-ysin(m^{\circ})+12sin(m^{\circ})=36-x \\ xsin(m^{\circ})-ycos(m^{\circ})=24-x \end{cases}$

From the first 2 equations, we get $m=90$, substituting into the 3rd equation, we get $x+y=18$.

Therefore, $m+x+y=90+18=\boxed{108}$

~VitalsBat

Solution 8

It is clear that $\bigtriangleup CPC'$ is a $45-45-90$ right triangle so $m=90$. We use the $\tan$ angle formula, $\tan{(a-b)}=\frac{\tan(a)-\tan(b)}{1+\tan(a)\tan(b)}$ to find the slope of line $CP$. We know that line $CC'$ has slope $\frac{1}{4}$ and let $b=-45^{\circ}$, then plugging both values into the formula, we find that the slope of $CP$ is $\frac{-3}{5}$. Also, $CC'$ has length $\sqrt{34}$. Create a right triangle $KCP$ where $KP$ is parallel to the $x$ axis and $CP$ is the hypotenuse. Then $CK=3x$ and $KP=5x$ and doing Pythagorean on $\bigtriangleup KCP$ gives $x=1$. Therefore, we know that $P$ is a translation 3 units down and 5 units right from $C(16,0)$, from which we obtain $P(21,-3)$. Adding the three variables, we obtain $90+21-3=\boxed{108}$

~Magnetoninja

See Also

2020 AIME II (Problems • Answer Key • Resources)
Preceded by
Problem 3 		Followed by
Problem 5
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2020_AIME_II_Problems/Problem_4&oldid=211314"