Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus
ONLINE AMC 8 PREP WITH AOPS
Top scorers around the country use AoPS. Join training courses for beginners and advanced students.
VIEW CATALOG

Difference between revisions of "2022 AMC 8 Problems"

(→‎Problem 19)
(Undo revision 221767 by Matthew.c (talk))
(Tag: Undo)
 
(116 intermediate revisions by 35 users not shown)
Line 1: Line 1:
−
IMPORTANT: When copied a problem, replace the X's for answer choices.
+
{{AMC8 Problems|year=2022|}}
−
 
 
 
==Problem 1==
 
==Problem 1==
  
Line 6: Line 5:
  
 
<asy>
 
<asy>
−
usepackage("mathptmx");
 
 
defaultpen(linewidth(0.5));
 
defaultpen(linewidth(0.5));
 
size(5cm);
 
size(5cm);
Line 152: Line 150:
 
}
 
}
 
label("8\tiny{\textsc{am}}",sh+(1,-.2),S);
 
label("8\tiny{\textsc{am}}",sh+(1,-.2),S);
−
 
+
 
for (int i=2;i<9;++i) {
 
for (int i=2;i<9;++i) {
 
label(string(mod12(i+7)),sh+(i,-.2),S);
 
label(string(mod12(i+7)),sh+(i,-.2),S);
Line 161: Line 159:
 
}
 
}
 
draw(rotate(90)*"Distance (miles)",sh+(-2.1,3),fontsize(10));
 
draw(rotate(90)*"Distance (miles)",sh+(-2.1,3),fontsize(10));
−
label("$\textbf{("+lab+")}$",sh+(-2.1,6.8),fontsize(10));
+
label("$\textbf{("+lab+")}$",sh+(-2.1,6.8),fontsize(12));
 
}
 
}
 
drawgraph((0,0),"A");
 
drawgraph((0,0),"A");
Line 197: Line 195:
 
==Problem 12==
 
==Problem 12==
  
−
<math>\textbf{(A) } X\qquad\textbf{(B) } X\qquad\textbf{(C) } X\qquad\textbf{(D) } X\qquad\textbf{(E) } X</math>
+
The arrows on the two spinners shown below are spun. Let the number <math>N</math>  equal <math>10</math> times the number on Spinner <math>\text{A}</math>, added to the number on Spinner <math>\text{B}</math>. What is the probability that <math>N</math> is a perfect square number?
 +
<asy>
 +
//diagram by pog give me 1 billion dollars for this
 +
size(6cm);
 +
usepackage("mathptmx");
 +
filldraw(arc((0,0), r=4, angle1=0, angle2=90)--(0,0)--cycle,mediumgray*0.5+gray*0.5);
 +
filldraw(arc((0,0), r=4, angle1=90, angle2=180)--(0,0)--cycle,lightgray);
 +
filldraw(arc((0,0), r=4, angle1=180, angle2=270)--(0,0)--cycle,mediumgray);
 +
filldraw(arc((0,0), r=4, angle1=270, angle2=360)--(0,0)--cycle,lightgray*0.5+mediumgray*0.5);
 +
label("$5$", (-1.5,1.7));
 +
label("$6$", (1.5,1.7));
 +
label("$7$", (1.5,-1.7));
 +
label("$8$", (-1.5,-1.7));
 +
label("Spinner A", (0, -5.5));
 +
filldraw(arc((12,0), r=4, angle1=0, angle2=90)--(12,0)--cycle,mediumgray*0.5+gray*0.5);
 +
filldraw(arc((12,0), r=4, angle1=90, angle2=180)--(12,0)--cycle,lightgray);
 +
filldraw(arc((12,0), r=4, angle1=180, angle2=270)--(12,0)--cycle,mediumgray);
 +
filldraw(arc((12,0), r=4, angle1=270, angle2=360)--(12,0)--cycle,lightgray*0.5+mediumgray*0.5);
 +
label("$1$", (10.5,1.7));
 +
label("$2$", (13.5,1.7));
 +
label("$3$", (13.5,-1.7));
 +
label("$4$", (10.5,-1.7));
 +
label("Spinner B", (12, -5.5));
 +
</asy>
 +
<math>\textbf{(A)} ~\dfrac{1}{16}\qquad\textbf{(B)} ~\dfrac{1}{8}\qquad\textbf{(C)} ~\dfrac{1}{4}\qquad\textbf{(D)} ~\dfrac{3}{8}\qquad\textbf{(E)} ~\dfrac{1}{2}</math>
  
 
[[2022 AMC 8 Problems/Problem 12|Solution]]
 
[[2022 AMC 8 Problems/Problem 12|Solution]]
Line 207: Line 229:
 
“One positive integer is _____ more than twice another, and the sum of the two numbers is <math>28</math>.”
 
“One positive integer is _____ more than twice another, and the sum of the two numbers is <math>28</math>.”
  
−
<math>\textbf{(A)} ~6\qquad\textbf{(B)} ~7\qquad\textbf{(C)} ~8\qquad\textbf{(D)} ~9\qquad\textbf{(E)} ~10</math>
+
<math>\textbf{(A) } 6 \qquad \textbf{(B) } 7 \qquad \textbf{(C) } 8 \qquad \textbf{(D) } 9 \qquad \textbf{(E) } 10</math>
  
 
[[2022 AMC 8 Problems/Problem 13|Solution]]
 
[[2022 AMC 8 Problems/Problem 13|Solution]]
Line 213: Line 235:
 
==Problem 14==
 
==Problem 14==
  
−
In how many ways can the letters in <math>BEEKEEPER</math> be rearranged so that two or more <math>E</math>s do not appear together?
+
In how many ways can the letters in <math>\textbf{BEEKEEPER}</math> be rearranged so that two or more <math>\textbf{E}</math>s do not appear together?
  
 
<math>\textbf{(A) } 1 \qquad \textbf{(B) } 4 \qquad \textbf{(C) } 12 \qquad \textbf{(D) } 24 \qquad \textbf{(E) } 120</math>
 
<math>\textbf{(A) } 1 \qquad \textbf{(B) } 4 \qquad \textbf{(C) } 12 \qquad \textbf{(D) } 24 \qquad \textbf{(E) } 120</math>
Line 239: Line 261:
 
label(scale(0.7)*"$4$", (-0.3,4), black);
 
label(scale(0.7)*"$4$", (-0.3,4), black);
 
label(scale(0.7)*"$5$", (-0.3,5), black);
 
label(scale(0.7)*"$5$", (-0.3,5), black);
−
label(scale(0.75)*rotate(90)*"Price (dollars)", (-1,3.2), black);
+
label(scale(0.8)*rotate(90)*"Price (dollars)", (-1,3.2), black);
−
label(scale(0.75)*"Weight (ounces)", (3.2,-1), black);
+
label(scale(0.8)*"Weight (ounces)", (3.2,-1), black);
 
dot((1,1.2),black);
 
dot((1,1.2),black);
 
dot((1,1.7),black);
 
dot((1,1.7),black);
Line 295: Line 317:
 
==Problem 17==
 
==Problem 17==
  
−
If <math>n</math> is an even positive integer, the <i>double factorial</i> notation <math>n!!</math> represents the product of all the even integers from <math>2</math> to <math>n</math>. For example, <math>8!! = 2 \cdot 4 \cdot 6 \cdot 8</math>. What is the units digit of the following sum? <cmath>2!! + 4!! + 6!! + \cdots + 2018!! + 2020!! + 2022!!</cmath>
+
If <math>n</math> is an even positive integer, the <math>\emph{double factorial}</math> notation <math>n!!</math> represents the product of all the even integers from <math>2</math> to <math>n</math>. For example, <math>8!! = 2 \cdot 4 \cdot 6 \cdot 8</math>. What is the units digit of the following sum? <cmath>2!! + 4!! + 6!! + \cdots + 2018!! + 2020!! + 2022!!</cmath>
  
 
<math>\textbf{(A)} ~0\qquad\textbf{(B)} ~2\qquad\textbf{(C)} ~4\qquad\textbf{(D)} ~6\qquad\textbf{(E)} ~8</math>
 
<math>\textbf{(A)} ~0\qquad\textbf{(B)} ~2\qquad\textbf{(C)} ~4\qquad\textbf{(D)} ~6\qquad\textbf{(E)} ~8</math>
Line 348: Line 370:
 
label("$100$", (7.5,-0.1));
 
label("$100$", (7.5,-0.1));
 
</asy>
 
</asy>
 +
 
Later Mr. Ramos discovered that there was a scoring error on one of the questions. He regraded the tests, awarding some of the students <math>5</math> extra points, which increased the median test score to <math>85</math>. What is the minimum number of students who received extra points?
 
Later Mr. Ramos discovered that there was a scoring error on one of the questions. He regraded the tests, awarding some of the students <math>5</math> extra points, which increased the median test score to <math>85</math>. What is the minimum number of students who received extra points?
  
Line 358: Line 381:
 
==Problem 20==
 
==Problem 20==
  
−
<math>\textbf{(A) } X \qquad \textbf{(B) } X \qquad \textbf{(C) } X \qquad \textbf{(D) } X \qquad \textbf{(E) } X</math>
+
The grid below is to be filled with integers in such a way that the sum of the numbers in each row and the sum of the numbers in each column are the same. Four numbers are missing. The number <math>x</math> in the lower left corner is larger than the other three missing numbers. What is the smallest possible value of <math>x</math>?
 +
<asy>
 +
unitsize(0.5cm);
 +
draw((3,3)--(-3,3));
 +
draw((3,1)--(-3,1));
 +
draw((3,-3)--(-3,-3));
 +
draw((3,-1)--(-3,-1));
 +
draw((3,3)--(3,-3));
 +
draw((1,3)--(1,-3));
 +
draw((-3,3)--(-3,-3));
 +
draw((-1,3)--(-1,-3));
 +
label((-2,2),"$-2$");
 +
label((0,2),"$9$");
 +
label((2,2),"$5$");
 +
label((2,0),"${-}1$");
 +
label((2,-2),"$8$");
 +
label((-2,-2),"$x$");
 +
</asy>
 +
<math>\textbf{(A) } {-}1 \qquad \textbf{(B) } 5 \qquad \textbf{(C) } 6 \qquad \textbf{(D) } 8 \qquad \textbf{(E) } 9</math>
  
 
[[2022 AMC 8 Problems/Problem 20|Solution]]
 
[[2022 AMC 8 Problems/Problem 20|Solution]]
Line 364: Line 405:
 
==Problem 21==
 
==Problem 21==
  
−
<math>\textbf{(A) } X \qquad \textbf{(B) } X \qquad \textbf{(C) } X \qquad \textbf{(D) } X \qquad \textbf{(E) } X</math>
+
Steph scored <math>15</math> baskets out of <math>20</math> attempts in the first half of a game, and <math>10</math> baskets out of <math>10</math> attempts in the second half. Candace took <math>12</math> attempts in the first half and <math>18</math> attempts in the second. In each half, Steph scored a higher percentage of baskets than Candace. Surprisingly they ended with the same overall percentage of baskets scored. How many more baskets did Candace score in the second half than in the first?
 +
<asy>
 +
size(7cm);
 +
draw((-8,27)--(72,27));
 +
draw((16,0)--(16,35));
 +
draw((40,0)--(40,35));
 +
label("12", (28,3));
 +
draw((25,6.5)--(25,12)--(31,12)--(31,6.5)--cycle);
 +
draw((25,5.5)--(31,5.5));
 +
label("18", (56,3));
 +
draw((53,6.5)--(53,12)--(59,12)--(59,6.5)--cycle);
 +
draw((53,5.5)--(59,5.5));
 +
draw((53,5.5)--(59,5.5));
 +
label("20", (28,18));
 +
label("15", (28,24));
 +
draw((25,21)--(31,21));
 +
label("10", (56,18));
 +
label("10", (56,24));
 +
draw((53,21)--(59,21));
 +
label("First Half", (28,31));
 +
label("Second Half", (56,31));
 +
label("Candace", (2.35,6));
 +
label("Steph", (0,21));
 +
</asy>
 +
<math>\textbf{(A) } 7\qquad\textbf{(B) } 8\qquad\textbf{(C) } 9\qquad\textbf{(D) } 10\qquad\textbf{(E) } 11</math>
  
 
[[2022 AMC 8 Problems/Problem 21|Solution]]
 
[[2022 AMC 8 Problems/Problem 21|Solution]]
  
 
==Problem 22==
 
==Problem 22==
 +
A bus takes <math>2</math> minutes to drive from one stop to the next, and waits <math>1</math> minute at each stop to let passengers board. Zia takes <math>5</math> minutes to walk from one bus stop to the next. As Zia reaches a bus stop, if the bus is at the previous stop or has already left the previous stop, then she will wait for the bus. Otherwise she will start walking toward the next stop. Suppose the bus and Zia start at the same time toward the library, with the bus <math>3</math> stops behind. After how many minutes will Zia board the bus?
  
−
<math>\textbf{(A) } X \qquad \textbf{(B) } X \qquad \textbf{(C) } X \qquad \textbf{(D) } X \qquad \textbf{(E) } X</math>
+
[[File:2022 AMC 8 Problem 22 Diagram.png|750px|center]]
 +
 
 +
<math>\textbf{(A) } 17 \qquad \textbf{(B) } 19 \qquad \textbf{(C) } 20 \qquad \textbf{(D) } 21 \qquad \textbf{(E) } 23</math>
  
 
[[2022 AMC 8 Problems/Problem 22|Solution]]
 
[[2022 AMC 8 Problems/Problem 22|Solution]]
  
 
==Problem 23==
 
==Problem 23==
 +
A <math>\triangle</math> or <math>\bigcirc</math> is placed in each of the nine squares in a <math>3</math>-by-<math>3</math> grid. Shown below is a sample configuration with three <math>\triangle</math>s in a line.
 +
<asy>
 +
//diagram by kante314
 +
size(3.3cm);
 +
defaultpen(linewidth(1));
 +
real r = 0.37;
 +
path equi = r * dir(-30) -- (r+0.03) * dir(90) -- r * dir(210) -- cycle;
 +
draw((0,0)--(0,3)--(3,3)--(3,0)--cycle);
 +
draw((0,1)--(3,1)--(3,2)--(0,2)--cycle);
 +
draw((1,0)--(1,3)--(2,3)--(2,0)--cycle);
 +
draw(circle((3/2,5/2),1/3));
 +
draw(circle((5/2,1/2),1/3));
 +
draw(circle((3/2,3/2),1/3));
 +
draw(shift(0.5,0.38) * equi);
 +
draw(shift(1.5,0.38) * equi);
 +
draw(shift(0.5,1.38) * equi);
 +
draw(shift(2.5,1.38) * equi);
 +
draw(shift(0.5,2.38) * equi);
 +
draw(shift(2.5,2.38) * equi);
 +
</asy>
 +
How many configurations will have three <math>\triangle</math>s in a line and three <math>\bigcirc</math>s in a line?
  
−
<math>\textbf{(A) } X \qquad \textbf{(B) } X \qquad \textbf{(C) } X \qquad \textbf{(D) } X \qquad \textbf{(E) } X</math>
+
<math>\textbf{(A) } 39 \qquad \textbf{(B) } 42 \qquad \textbf{(C) } 78 \qquad \textbf{(D) } 84 \qquad \textbf{(E) } 96</math>
  
 
[[2022 AMC 8 Problems/Problem 23|Solution]]
 
[[2022 AMC 8 Problems/Problem 23|Solution]]
Line 386: Line 475:
 
<asy>
 
<asy>
 
usepackage("mathptmx");
 
usepackage("mathptmx");
−
unitsize(1cm);
+
size(275);
−
defaultpen(linewidth(0.7)+fontsize(11));
+
defaultpen(linewidth(0.8));
 
real r = 2, s = 2.5, theta = 14;
 
real r = 2, s = 2.5, theta = 14;
 
pair G = (0,0), F = (r,0), C = (r,s), B = (0,s), M = (C+F)/2, I = M + s/2 * dir(-theta);
 
pair G = (0,0), F = (r,0), C = (r,s), B = (0,s), M = (C+F)/2, I = M + s/2 * dir(-theta);
Line 400: Line 489:
 
dot("$D$",D,dir(0));
 
dot("$D$",D,dir(0));
 
dot("$E$",E,S);
 
dot("$E$",E,S);
−
dot("$F$",F,1.5*S);
+
dot("$F$",F,1.5*dir(-100));
 
dot("$G$",G,S);
 
dot("$G$",G,S);
 
dot("$H$",H,W);
 
dot("$H$",H,W);
Line 407: Line 496:
 
</asy>
 
</asy>
  
−
<math>\textbf{(A)} ~112\qquad\textbf{(B)} ~128\qquad\textbf{(C)} ~192\qquad\textbf{(D)} ~240\qquad\textbf{(E)} ~288\qquad</math>
+
<math>\textbf{(A)} ~112\qquad\textbf{(B)} ~128\qquad\textbf{(C)} ~192\qquad\textbf{(D)} ~240\qquad\textbf{(E)} ~288</math>
  
 
[[2022 AMC 8 Problems/Problem 24|Solution]]
 
[[2022 AMC 8 Problems/Problem 24|Solution]]
Line 413: Line 502:
 
==Problem 25==
 
==Problem 25==
  
−
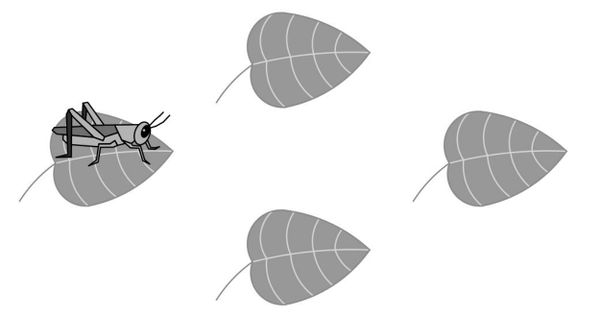
<math>\textbf{(A) } X \qquad \textbf{(B) } X \qquad \textbf{(C) } X \qquad \textbf{(D) } X \qquad \textbf{(E) } X</math>
+
A cricket randomly hops between <math>4</math> leaves, on each turn hopping to one of the other <math>3</math> leaves with equal probability. After <math>4</math> hops, what is the probability that the cricket has returned to the leaf where it started?
 +
 
 +
[[File:2022 AMC 8 Problem 25 Picture.jpg|center|600px]]
 +
 
 +
<math>\textbf{(A) }\frac{2}{9}\qquad\textbf{(B) }\frac{19}{80}\qquad\textbf{(C) }\frac{20}{81}\qquad\textbf{(D) }\frac{1}{4}\qquad\textbf{(E) }\frac{7}{27}</math>
  
 
[[2022 AMC 8 Problems/Problem 25|Solution]]
 
[[2022 AMC 8 Problems/Problem 25|Solution]]
 +
 +
==See Also==
 +
{{AMC8 box|year=2022|before=[[2020 AMC 8 Problems|2020 AMC 8]]|after=[[2023 AMC 8 Problems|2023 AMC 8]]}}
 +
* [[AMC 8]]
 +
* [[AMC 8 Problems and Solutions]]
 +
* [[Mathematics competition resources|Mathematics Competition Resources]]

Latest revision as of 13:53, 6 July 2024

2022 AMC 8 (Answer Key)
Printable versions: Wiki • AoPS Resources • PDF

Instructions

  1. This is a 25-question, multiple choice test. Each question is followed by answers marked A, B, C, D and E. Only one of these is correct.
  2. You will receive 1 point for each correct answer. There is no penalty for wrong answers.
  3. No aids are permitted other than plain scratch paper, writing utensils, ruler, and erasers. In particular, graph paper, compass, protractor, calculators, computers, smartwatches, and smartphones are not permitted. Rules
  4. Figures are not necessarily drawn to scale.
  5. You will have 40 minutes working time to complete the test.
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25

Problem 1

The Math Team designed a logo shaped like a multiplication symbol, shown below on a grid of 1-inch squares. What is the area of the logo in square inches?

[asy] defaultpen(linewidth(0.5)); size(5cm); defaultpen(fontsize(14pt)); label("$\textbf{Math}$", (2.1,3.7)--(3.9,3.7)); label("$\textbf{Team}$", (2.1,3)--(3.9,3)); filldraw((1,2)--(2,1)--(3,2)--(4,1)--(5,2)--(4,3)--(5,4)--(4,5)--(3,4)--(2,5)--(1,4)--(2,3)--(1,2)--cycle, mediumgray*0.5 + lightgray*0.5); draw((0,0)--(6,0), gray); draw((0,1)--(6,1), gray); draw((0,2)--(6,2), gray); draw((0,3)--(6,3), gray); draw((0,4)--(6,4), gray); draw((0,5)--(6,5), gray); draw((0,6)--(6,6), gray); draw((0,0)--(0,6), gray); draw((1,0)--(1,6), gray); draw((2,0)--(2,6), gray); draw((3,0)--(3,6), gray); draw((4,0)--(4,6), gray); draw((5,0)--(5,6), gray); draw((6,0)--(6,6), gray); [/asy]

$\textbf{(A) } 10 \qquad \textbf{(B) } 12 \qquad \textbf{(C) } 13 \qquad \textbf{(D) } 14 \qquad \textbf{(E) } 15$

Solution

Problem 2

Consider these two operations: \begin{align*} a \, \blacklozenge \, b &= a^2 - b^2\\ a \, \bigstar \, b &= (a - b)^2 \end{align*} What is the value of $(5 \, \blacklozenge \, 3) \, \bigstar \, 6?$

$\textbf{(A) } {-}20 \qquad \textbf{(B) } 4 \qquad \textbf{(C) } 16 \qquad \textbf{(D) } 100 \qquad \textbf{(E) } 220$

Solution

Problem 3

When three positive integers $a$, $b$, and $c$ are multiplied together, their product is $100$. Suppose $a < b < c$. In how many ways can the numbers be chosen?

$\textbf{(A) } 0 \qquad \textbf{(B) } 1\qquad\textbf{(C) } 2\qquad\textbf{(D) } 3\qquad\textbf{(E) } 4$

Solution

Problem 4

The letter M in the figure below is first reflected over the line $q$ and then reflected over the line $p$. What is the resulting image?

[asy] // pog diagram usepackage("newtxtext"); size(3cm); draw((-1,0)--(1,0)); draw((0,-1)--(0,1)); label("$\textbf{\textsf{M}}$",(0.25,0.6)); draw((-0.8,-0.8)--(0.8,0.8),linewidth(1.1)); label("$p$", (-1,0),NE); label("$q$", (-0.75,-0.75), N*1.5); [/asy]

[asy] // pog diagram usepackage("newtxtext"); size(12.5cm); draw((-1,0)--(1,0)); draw((0,-1)--(0,1)); label(rotate(90)*"$\textbf{\textsf{M}}$",(0.6,-0.25)); draw((-0.8,-0.8)--(0.8,0.8),linewidth(1.1)); label("$\textbf{(A)}$",(-1,1),W); draw((2,0)--(4,0)); draw((3,-1)--(3,1)); label(rotate(270)*"$\textbf{\textsf{M}}$",(2.8,0.7)); draw((2.2,-0.8)--(3.8,0.8),linewidth(1.1)); label("$\textbf{(B)}$",(2,1),W); draw((5,0)--(7,0)); draw((6,-1)--(6,1)); label(rotate(90)*"$\textbf{\textsf{M}}$",(5.4,0.2)); draw((5.2,-0.8)--(6.8,0.8),linewidth(1.1)); label("$\textbf{(C)}$",(5,1),W); draw((-1,-2.5)--(1,-2.5)); draw((0,-3.5)--(0,-1.5)); label(rotate(180)*"$\textbf{\textsf{M}}$",(-0.25,-3.1)); draw((-0.8,-3.3)--(0.8,-1.7),linewidth(1.1)); label("$\textbf{(D)}$",(-1,-1.5),W); draw((2,-2.5)--(4,-2.5)); draw((3,-3.5)--(3,-1.5)); label(rotate(270)*"$\textbf{\textsf{M}}$",(3.6,-2.75)); draw((2.2,-3.3)--(3.8,-1.7),linewidth(1.1)); label("$\textbf{(E)}$",(2,-1.5),W); [/asy]

Solution

Problem 5

Anna and Bella are celebrating their birthdays together. Five years ago, when Bella turned $6$ years old, she received a newborn kitten as a birthday present. Today the sum of the ages of the two children and the kitten is $30$ years. How many years older than Bella is Anna?

$\textbf{(A) } 1 \qquad \textbf{(B) } 2 \qquad \textbf{(C) } 3 \qquad \textbf{(D) } 4 \qquad \textbf{(E) } ~5$

Solution

Problem 6

Three positive integers are equally spaced on a number line. The middle number is $15,$ and the largest number is $4$ times the smallest number. What is the smallest of these three numbers?

$\textbf{(A) } 4 \qquad \textbf{(B) } 5 \qquad \textbf{(C) } 6 \qquad \textbf{(D) } 7 \qquad \textbf{(E) } 8$

Solution

Problem 7

When the World Wide Web first became popular in the $1990$s, download speeds reached a maximum of about $56$ kilobits per second. Approximately how many minutes would the download of a $4.2$-megabyte song have taken at that speed? (Note that there are $8000$ kilobits in a megabyte.)

$\textbf{(A) } 0.6 \qquad \textbf{(B) } 10 \qquad \textbf{(C) } 1800 \qquad \textbf{(D) } 7200 \qquad \textbf{(E) } 36000$

Solution

Problem 8

What is the value of \[\frac{1}{3}\cdot\frac{2}{4}\cdot\frac{3}{5}\cdots\frac{18}{20}\cdot\frac{19}{21}\cdot\frac{20}{22}?\]

$\textbf{(A) } \frac{1}{462} \qquad \textbf{(B) } \frac{1}{231} \qquad \textbf{(C) } \frac{1}{132} \qquad \textbf{(D) } \frac{2}{213} \qquad \textbf{(E) } \frac{1}{22}$

Solution

Problem 9

A cup of boiling water ($212^{\circ}\text{F}$) is placed to cool in a room whose temperature remains constant at $68^{\circ}\text{F}$. Suppose the difference between the water temperature and the room temperature is halved every $5$ minutes. What is the water temperature, in degrees Fahrenheit, after $15$ minutes?

$\textbf{(A)} ~77\qquad\textbf{(B)} ~86\qquad\textbf{(C)} ~92\qquad\textbf{(D)} ~98\qquad\textbf{(E)} ~104$

Solution

Problem 10

One sunny day, Ling decided to take a hike in the mountains. She left her house at $8 \, \textsc{am}$, drove at a constant speed of $45$ miles per hour, and arrived at the hiking trail at $10 \, \textsc{am}$. After hiking for $3$ hours, Ling drove home at a constant speed of $60$ miles per hour. Which of the following graphs best illustrates the distance between Ling’s car and her house over the course of her trip?

[asy] unitsize(12); usepackage("mathptmx"); defaultpen(fontsize(8)+linewidth(.7)); int mod12(int i) {if (i<13) {return i;} else {return i-12;}} void drawgraph(pair sh,string lab) { for (int i=0;i<11;++i) { for (int j=0;j<6;++j) { draw(shift(sh+(i,j))*unitsquare,mediumgray); } } draw(shift(sh)*((-1,0)--(11,0)),EndArrow(angle=20,size=8)); draw(shift(sh)*((0,-1)--(0,6)),EndArrow(angle=20,size=8)); for (int i=1;i<10;++i) { draw(shift(sh)*((i,-.2)--(i,.2))); } label("8\tiny{\textsc{am}}",sh+(1,-.2),S); for (int i=2;i<9;++i) { label(string(mod12(i+7)),sh+(i,-.2),S); } label("4\tiny{\textsc{pm}}",sh+(9,-.2),S); for (int i=1;i<6;++i) { label(string(30*i),sh+(0,i),2*W); } draw(rotate(90)*"Distance (miles)",sh+(-2.1,3),fontsize(10)); label("$\textbf{("+lab+")}$",sh+(-2.1,6.8),fontsize(12)); } drawgraph((0,0),"A"); drawgraph((15,0),"B"); drawgraph((0,-10),"C"); drawgraph((15,-10),"D"); drawgraph((0,-20),"E"); dotfactor=6; draw((1,0)--(3,3)--(6,3)--(8,0),linewidth(.9)); dot((1,0)^^(3,3)^^(6,3)^^(8,0)); pair sh = (15,0); draw(shift(sh)*((1,0)--(3,1.5)--(6,1.5)--(8,0)),linewidth(.9)); dot(sh+(1,0)^^sh+(3,1.5)^^sh+(6,1.5)^^sh+(8,0)); pair sh = (0,-10); draw(shift(sh)*((1,0)--(3,1.5)--(6,1.5)--(7.5,0)),linewidth(.9)); dot(sh+(1,0)^^sh+(3,1.5)^^sh+(6,1.5)^^sh+(7.5,0)); pair sh = (15,-10); draw(shift(sh)*((1,0)--(3,4)--(6,4)--(9.3,0)),linewidth(.9)); dot(sh+(1,0)^^sh+(3,4)^^sh+(6,4)^^sh+(9.3,0)); pair sh = (0,-20); draw(shift(sh)*((1,0)--(3,3)--(6,3)--(7.5,0)),linewidth(.9)); dot(sh+(1,0)^^sh+(3,3)^^sh+(6,3)^^sh+(7.5,0)); [/asy]

Solution

Problem 11

Henry the donkey has a very long piece of pasta. He takes a number of bites of pasta, each time eating $3$ inches of pasta from the middle of one piece. In the end, he has $10$ pieces of pasta whose total length is $17$ inches. How long, in inches, was the piece of pasta he started with?

$\textbf{(A)} ~34\qquad\textbf{(B)} ~38\qquad\textbf{(C)} ~41\qquad\textbf{(D)} ~44\qquad\textbf{(E)} ~47$

Solution

Problem 12

The arrows on the two spinners shown below are spun. Let the number $N$ equal $10$ times the number on Spinner $\text{A}$, added to the number on Spinner $\text{B}$. What is the probability that $N$ is a perfect square number? [asy] //diagram by pog give me 1 billion dollars for this size(6cm); usepackage("mathptmx"); filldraw(arc((0,0), r=4, angle1=0, angle2=90)--(0,0)--cycle,mediumgray*0.5+gray*0.5); filldraw(arc((0,0), r=4, angle1=90, angle2=180)--(0,0)--cycle,lightgray); filldraw(arc((0,0), r=4, angle1=180, angle2=270)--(0,0)--cycle,mediumgray); filldraw(arc((0,0), r=4, angle1=270, angle2=360)--(0,0)--cycle,lightgray*0.5+mediumgray*0.5); label("$5$", (-1.5,1.7)); label("$6$", (1.5,1.7)); label("$7$", (1.5,-1.7)); label("$8$", (-1.5,-1.7)); label("Spinner A", (0, -5.5)); filldraw(arc((12,0), r=4, angle1=0, angle2=90)--(12,0)--cycle,mediumgray*0.5+gray*0.5); filldraw(arc((12,0), r=4, angle1=90, angle2=180)--(12,0)--cycle,lightgray); filldraw(arc((12,0), r=4, angle1=180, angle2=270)--(12,0)--cycle,mediumgray); filldraw(arc((12,0), r=4, angle1=270, angle2=360)--(12,0)--cycle,lightgray*0.5+mediumgray*0.5); label("$1$", (10.5,1.7)); label("$2$", (13.5,1.7)); label("$3$", (13.5,-1.7)); label("$4$", (10.5,-1.7)); label("Spinner B", (12, -5.5)); [/asy] $\textbf{(A)} ~\dfrac{1}{16}\qquad\textbf{(B)} ~\dfrac{1}{8}\qquad\textbf{(C)} ~\dfrac{1}{4}\qquad\textbf{(D)} ~\dfrac{3}{8}\qquad\textbf{(E)} ~\dfrac{1}{2}$

Solution

Problem 13

How many positive integers can fill the blank in the sentence below?

“One positive integer is _____ more than twice another, and the sum of the two numbers is $28$.”

$\textbf{(A) } 6 \qquad \textbf{(B) } 7 \qquad \textbf{(C) } 8 \qquad \textbf{(D) } 9 \qquad \textbf{(E) } 10$

Solution

Problem 14

In how many ways can the letters in $\textbf{BEEKEEPER}$ be rearranged so that two or more $\textbf{E}$s do not appear together?

$\textbf{(A) } 1 \qquad \textbf{(B) } 4 \qquad \textbf{(C) } 12 \qquad \textbf{(D) } 24 \qquad \textbf{(E) } 120$

Solution

Problem 15

Laszlo went online to shop for black pepper and found thirty different black pepper options varying in weight and price, shown in the scatter plot below. In ounces, what is the weight of the pepper that offers the lowest price per ounce?

[asy] //diagram by pog size(5.5cm); usepackage("mathptmx"); defaultpen(mediumgray*0.5+gray*0.5+linewidth(0.63)); add(grid(6,6)); label(scale(0.7)*"$1$", (1,-0.3), black); label(scale(0.7)*"$2$", (2,-0.3), black); label(scale(0.7)*"$3$", (3,-0.3), black); label(scale(0.7)*"$4$", (4,-0.3), black); label(scale(0.7)*"$5$", (5,-0.3), black); label(scale(0.7)*"$1$", (-0.3,1), black); label(scale(0.7)*"$2$", (-0.3,2), black); label(scale(0.7)*"$3$", (-0.3,3), black); label(scale(0.7)*"$4$", (-0.3,4), black); label(scale(0.7)*"$5$", (-0.3,5), black); label(scale(0.8)*rotate(90)*"Price (dollars)", (-1,3.2), black); label(scale(0.8)*"Weight (ounces)", (3.2,-1), black); dot((1,1.2),black); dot((1,1.7),black); dot((1,2),black); dot((1,2.8),black); dot((1.5,2.1),black); dot((1.5,3),black); dot((1.5,3.3),black); dot((1.5,3.75),black); dot((2,2),black); dot((2,2.9),black); dot((2,3),black); dot((2,4),black); dot((2,4.35),black); dot((2,4.8),black); dot((2.5,2.7),black); dot((2.5,3.7),black); dot((2.5,4.2),black); dot((2.5,4.4),black); dot((3,2.5),black); dot((3,3.4),black); dot((3,4.2),black); dot((3.5,3.8),black); dot((3.5,4.5),black); dot((3.5,4.8),black); dot((4,3.9),black); dot((4,5.1),black); dot((4.5,4.75),black); dot((4.5,5),black); dot((5,4.5),black); dot((5,5),black); [/asy]

$\textbf{(A) }1\qquad\textbf{(B) }2\qquad\textbf{(C) }3\qquad\textbf{(D) }4\qquad\textbf{(E) }5$

Solution

Problem 16

Four numbers are written in a row. The average of the first two is $21,$ the average of the middle two is $26,$ and the average of the last two is $30.$ What is the average of the first and last of the numbers?

$\textbf{(A) } 24 \qquad \textbf{(B) } 25 \qquad \textbf{(C) } 26 \qquad \textbf{(D) } 27 \qquad \textbf{(E) } 28$

Solution

Problem 17

If $n$ is an even positive integer, the $\emph{double factorial}$ notation $n!!$ represents the product of all the even integers from $2$ to $n$. For example, $8!! = 2 \cdot 4 \cdot 6 \cdot 8$. What is the units digit of the following sum? \[2!! + 4!! + 6!! + \cdots + 2018!! + 2020!! + 2022!!\]

$\textbf{(A)} ~0\qquad\textbf{(B)} ~2\qquad\textbf{(C)} ~4\qquad\textbf{(D)} ~6\qquad\textbf{(E)} ~8$

Solution

Problem 18

The midpoints of the four sides of a rectangle are $(-3,0), (2,0), (5,4),$ and $(0,4).$ What is the area of the rectangle?

$\textbf{(A) } 20 \qquad \textbf{(B) } 25 \qquad \textbf{(C) } 40 \qquad \textbf{(D) } 50 \qquad \textbf{(E) } 80$

Solution

Problem 19

Mr. Ramos gave a test to his class of $20$ students. The dot plot below shows the distribution of test scores. [asy] //diagram by pog . give me 1,000,000,000 dollars for this diagram size(5cm); defaultpen(0.7); dot((0.5,1)); dot((0.5,1.5)); dot((1.5,1)); dot((1.5,1.5)); dot((2.5,1)); dot((2.5,1.5)); dot((2.5,2)); dot((2.5,2.5)); dot((3.5,1)); dot((3.5,1.5)); dot((3.5,2)); dot((3.5,2.5)); dot((3.5,3)); dot((4.5,1)); dot((4.5,1.5)); dot((5.5,1)); dot((5.5,1.5)); dot((5.5,2)); dot((6.5,1)); dot((7.5,1)); draw((0,0.5)--(8,0.5),linewidth(0.7)); defaultpen(fontsize(10.5pt)); label("$65$", (0.5,-0.1)); label("$70$", (1.5,-0.1)); label("$75$", (2.5,-0.1)); label("$80$", (3.5,-0.1)); label("$85$", (4.5,-0.1)); label("$90$", (5.5,-0.1)); label("$95$", (6.5,-0.1)); label("$100$", (7.5,-0.1)); [/asy]

Later Mr. Ramos discovered that there was a scoring error on one of the questions. He regraded the tests, awarding some of the students $5$ extra points, which increased the median test score to $85$. What is the minimum number of students who received extra points?

(Note that the median test score equals the average of the $2$ scores in the middle if the $20$ test scores are arranged in increasing order.)

$\textbf{(A)} ~2\qquad\textbf{(B)} ~3\qquad\textbf{(C)} ~4\qquad\textbf{(D)} ~5\qquad\textbf{(E)} ~6\qquad$

Solution

Problem 20

The grid below is to be filled with integers in such a way that the sum of the numbers in each row and the sum of the numbers in each column are the same. Four numbers are missing. The number $x$ in the lower left corner is larger than the other three missing numbers. What is the smallest possible value of $x$? [asy] unitsize(0.5cm); draw((3,3)--(-3,3)); draw((3,1)--(-3,1)); draw((3,-3)--(-3,-3)); draw((3,-1)--(-3,-1)); draw((3,3)--(3,-3)); draw((1,3)--(1,-3)); draw((-3,3)--(-3,-3)); draw((-1,3)--(-1,-3)); label((-2,2),"$-2$"); label((0,2),"$9$"); label((2,2),"$5$"); label((2,0),"${-}1$"); label((2,-2),"$8$"); label((-2,-2),"$x$"); [/asy] $\textbf{(A) } {-}1 \qquad \textbf{(B) } 5 \qquad \textbf{(C) } 6 \qquad \textbf{(D) } 8 \qquad \textbf{(E) } 9$

Solution

Problem 21

Steph scored $15$ baskets out of $20$ attempts in the first half of a game, and $10$ baskets out of $10$ attempts in the second half. Candace took $12$ attempts in the first half and $18$ attempts in the second. In each half, Steph scored a higher percentage of baskets than Candace. Surprisingly they ended with the same overall percentage of baskets scored. How many more baskets did Candace score in the second half than in the first? [asy] size(7cm); draw((-8,27)--(72,27)); draw((16,0)--(16,35)); draw((40,0)--(40,35)); label("12", (28,3)); draw((25,6.5)--(25,12)--(31,12)--(31,6.5)--cycle); draw((25,5.5)--(31,5.5)); label("18", (56,3)); draw((53,6.5)--(53,12)--(59,12)--(59,6.5)--cycle); draw((53,5.5)--(59,5.5)); draw((53,5.5)--(59,5.5)); label("20", (28,18)); label("15", (28,24)); draw((25,21)--(31,21)); label("10", (56,18)); label("10", (56,24)); draw((53,21)--(59,21)); label("First Half", (28,31)); label("Second Half", (56,31)); label("Candace", (2.35,6)); label("Steph", (0,21)); [/asy] $\textbf{(A) } 7\qquad\textbf{(B) } 8\qquad\textbf{(C) } 9\qquad\textbf{(D) } 10\qquad\textbf{(E) } 11$

Solution

Problem 22

A bus takes $2$ minutes to drive from one stop to the next, and waits $1$ minute at each stop to let passengers board. Zia takes $5$ minutes to walk from one bus stop to the next. As Zia reaches a bus stop, if the bus is at the previous stop or has already left the previous stop, then she will wait for the bus. Otherwise she will start walking toward the next stop. Suppose the bus and Zia start at the same time toward the library, with the bus $3$ stops behind. After how many minutes will Zia board the bus?

2022 AMC 8 Problem 22 Diagram.png

$\textbf{(A) } 17 \qquad \textbf{(B) } 19 \qquad \textbf{(C) } 20 \qquad \textbf{(D) } 21 \qquad \textbf{(E) } 23$

Solution

Problem 23

A $\triangle$ or $\bigcirc$ is placed in each of the nine squares in a $3$-by-$3$ grid. Shown below is a sample configuration with three $\triangle$s in a line. [asy] //diagram by kante314 size(3.3cm); defaultpen(linewidth(1)); real r = 0.37; path equi = r * dir(-30) -- (r+0.03) * dir(90) -- r * dir(210) -- cycle; draw((0,0)--(0,3)--(3,3)--(3,0)--cycle); draw((0,1)--(3,1)--(3,2)--(0,2)--cycle); draw((1,0)--(1,3)--(2,3)--(2,0)--cycle); draw(circle((3/2,5/2),1/3)); draw(circle((5/2,1/2),1/3)); draw(circle((3/2,3/2),1/3)); draw(shift(0.5,0.38) * equi); draw(shift(1.5,0.38) * equi); draw(shift(0.5,1.38) * equi); draw(shift(2.5,1.38) * equi); draw(shift(0.5,2.38) * equi); draw(shift(2.5,2.38) * equi); [/asy] How many configurations will have three $\triangle$s in a line and three $\bigcirc$s in a line?

$\textbf{(A) } 39 \qquad \textbf{(B) } 42 \qquad \textbf{(C) } 78 \qquad \textbf{(D) } 84 \qquad \textbf{(E) } 96$

Solution

Problem 24

The figure below shows a polygon $ABCDEFGH$, consisting of rectangles and right triangles. When cut out and folded on the dotted lines, the polygon forms a triangular prism. Suppose that $AH = EF = 8$ and $GH = 14$. What is the volume of the prism?

[asy] usepackage("mathptmx"); size(275); defaultpen(linewidth(0.8)); real r = 2, s = 2.5, theta = 14; pair G = (0,0), F = (r,0), C = (r,s), B = (0,s), M = (C+F)/2, I = M + s/2 * dir(-theta); pair N = (B+G)/2, J = N + s/2 * dir(180+theta); pair E = F + r * dir(- 45 - theta/2), D = I+E-F; pair H = J + r * dir(135 + theta/2), A = B+H-J; draw(A--B--C--I--D--E--F--G--J--H--cycle^^rightanglemark(F,I,C)^^rightanglemark(G,J,B)); draw(J--B--G^^C--F--I,linetype ("4 4")); dot("$A$",A,N); dot("$B$",B,1.2*N); dot("$C$",C,N); dot("$D$",D,dir(0)); dot("$E$",E,S); dot("$F$",F,1.5*dir(-100)); dot("$G$",G,S); dot("$H$",H,W); dot("$I$",I,NE); dot("$J$",J,1.5*S); [/asy]

$\textbf{(A)} ~112\qquad\textbf{(B)} ~128\qquad\textbf{(C)} ~192\qquad\textbf{(D)} ~240\qquad\textbf{(E)} ~288$

Solution

Problem 25

A cricket randomly hops between $4$ leaves, on each turn hopping to one of the other $3$ leaves with equal probability. After $4$ hops, what is the probability that the cricket has returned to the leaf where it started?

2022 AMC 8 Problem 25 Picture.jpg

$\textbf{(A) }\frac{2}{9}\qquad\textbf{(B) }\frac{19}{80}\qquad\textbf{(C) }\frac{20}{81}\qquad\textbf{(D) }\frac{1}{4}\qquad\textbf{(E) }\frac{7}{27}$

Solution

See Also

2022 AMC 8 (Problems • Answer Key • Resources)
Preceded by
2020 AMC 8 		Followed by
2023 AMC 8
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AJHSME/AMC 8 Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2022_AMC_8_Problems&oldid=221776"