Difference between revisions of "2022 AMC 8 Problems"

Latest revision as of 13:53, 6 July 2024

2022 AMC 8 (Answer Key) Printable versions: Wiki • AoPS Resources • PDF
Instructions This is a 25-question, multiple choice test. Each question is followed by answers marked A, B, C, D and E. Only one of these is correct. You will receive 1 point for each correct answer. There is no penalty for wrong answers. No aids are permitted other than plain scratch paper, writing utensils, ruler, and erasers. In particular, graph paper, compass, protractor, calculators, computers, smartwatches, and smartphones are not permitted. Rules Figures are not necessarily drawn to scale. You will have 40 minutes working time to complete the test.
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25

Problem 1

The Math Team designed a logo shaped like a multiplication symbol, shown below on a grid of 1-inch squares. What is the area of the logo in square inches?

$[asy] defaultpen(linewidth(0.5)); size(5cm); defaultpen(fontsize(14pt)); label("$\textbf{Math}$", (2.1,3.7)--(3.9,3.7)); label("$\textbf{Team}$", (2.1,3)--(3.9,3)); filldraw((1,2)--(2,1)--(3,2)--(4,1)--(5,2)--(4,3)--(5,4)--(4,5)--(3,4)--(2,5)--(1,4)--(2,3)--(1,2)--cycle, mediumgray*0.5 + lightgray*0.5); draw((0,0)--(6,0), gray); draw((0,1)--(6,1), gray); draw((0,2)--(6,2), gray); draw((0,3)--(6,3), gray); draw((0,4)--(6,4), gray); draw((0,5)--(6,5), gray); draw((0,6)--(6,6), gray); draw((0,0)--(0,6), gray); draw((1,0)--(1,6), gray); draw((2,0)--(2,6), gray); draw((3,0)--(3,6), gray); draw((4,0)--(4,6), gray); draw((5,0)--(5,6), gray); draw((6,0)--(6,6), gray); [/asy]$

$\textbf{(A) } 10 \qquad \textbf{(B) } 12 \qquad \textbf{(C) } 13 \qquad \textbf{(D) } 14 \qquad \textbf{(E) } 15$

@@ Line 1: / Line 1: @@
-IMPORTANT: THESE ARE NOT THE 2022 AMC 8 PROBLEMS. THIS IS COPY PASTED FROM THE 2020 AMC 8 PROBLEMS WIKI PAGE.
+{{AMC8 Problems|year=2022|}}
 ==Problem 1==
@@ Line 6: / Line 5: @@
 <asy>
-usepackage("mathptmx");
 defaultpen(linewidth(0.5));
 size(5cm);
@@ Line 13: / Line 11: @@
 label("$\textbf{Team}$", (2.1,3)--(3.9,3));
 filldraw((1,2)--(2,1)--(3,2)--(4,1)--(5,2)--(4,3)--(5,4)--(4,5)--(3,4)--(2,5)--(1,4)--(2,3)--(1,2)--cycle, mediumgray*0.5 + lightgray*0.5);
 draw((0,0)--(6,0), gray);
@@ Line 38: / Line 35: @@
 ==Problem 2==
-[[2020 AMC 8 Problems/Problem 2|Solution]]
+Consider these two operations:
+<cmath>\begin{align*}
+a \, \blacklozenge \, b &= a^2 - b^2\\
+a \, \bigstar \, b &= (a - b)^2
+\end{align*}</cmath>
+What is the value of <math>(5 \, \blacklozenge \, 3) \, \bigstar \, 6?</math>
+<math>\textbf{(A) } {-}20 \qquad \textbf{(B) } 4 \qquad \textbf{(C) } 16 \qquad \textbf{(D) } 100 \qquad \textbf{(E) } 220</math>
+[[2022 AMC 8 Problems/Problem 2|Solution]]
 ==Problem 3==
-[[2020 AMC 8 Problems/Problem 3|Solution]]
+When three positive integers <math>a</math>, <math>b</math>, and <math>c</math> are multiplied together, their product is <math>100</math>. Suppose <math>a < b < c</math>. In how many ways can the numbers be chosen?
+<math>\textbf{(A) } 0 \qquad \textbf{(B) } 1\qquad\textbf{(C) } 2\qquad\textbf{(D) } 3\qquad\textbf{(E) } 4</math>
+[[2022 AMC 8 Problems/Problem 3|Solution]]
 ==Problem 4==
-[[2020 AMC 8 Problems/Problem 4|Solution]]
+The letter <b>M</b> in the figure below is first reflected over the line <math>q</math> and then reflected over the line <math>p</math>. What is the resulting image?
+<asy>
+// pog diagram
+usepackage("newtxtext");
+size(3cm);
+draw((-1,0)--(1,0)); draw((0,-1)--(0,1)); label("$\textbf{\textsf{M}}$",(0.25,0.6));
+draw((-0.8,-0.8)--(0.8,0.8),linewidth(1.1)); label("$p$", (-1,0),NE); label("$q$", (-0.75,-0.75), N*1.5);
+</asy>
+<asy>
+// pog diagram
+usepackage("newtxtext");
+size(12.5cm);
+draw((-1,0)--(1,0)); draw((0,-1)--(0,1)); label(rotate(90)*"$\textbf{\textsf{M}}$",(0.6,-0.25));
+draw((-0.8,-0.8)--(0.8,0.8),linewidth(1.1));
+label("$\textbf{(A)}$",(-1,1),W);
+draw((2,0)--(4,0)); draw((3,-1)--(3,1)); label(rotate(270)*"$\textbf{\textsf{M}}$",(2.8,0.7));
+draw((2.2,-0.8)--(3.8,0.8),linewidth(1.1));
+label("$\textbf{(B)}$",(2,1),W);
+draw((5,0)--(7,0)); draw((6,-1)--(6,1)); label(rotate(90)*"$\textbf{\textsf{M}}$",(5.4,0.2));
+draw((5.2,-0.8)--(6.8,0.8),linewidth(1.1));
+label("$\textbf{(C)}$",(5,1),W);
+draw((-1,-2.5)--(1,-2.5)); draw((0,-3.5)--(0,-1.5)); label(rotate(180)*"$\textbf{\textsf{M}}$",(-0.25,-3.1));
+draw((-0.8,-3.3)--(0.8,-1.7),linewidth(1.1));
+label("$\textbf{(D)}$",(-1,-1.5),W);
+draw((2,-2.5)--(4,-2.5)); draw((3,-3.5)--(3,-1.5)); label(rotate(270)*"$\textbf{\textsf{M}}$",(3.6,-2.75));
+draw((2.2,-3.3)--(3.8,-1.7),linewidth(1.1));
+label("$\textbf{(E)}$",(2,-1.5),W);
+</asy>
+[[2022 AMC 8 Problems/Problem 4|Solution]]
 ==Problem 5==
-[[2020 AMC 8 Problems/Problem 5|Solution]]
+Anna and Bella are celebrating their birthdays together. Five years ago, when Bella turned <math>6</math> years old, she received a newborn kitten as a birthday present. Today the sum of the ages of the two children and the kitten is <math>30</math> years. How many years older than Bella is Anna?
+<math>\textbf{(A) } 1 \qquad \textbf{(B) } 2 \qquad \textbf{(C) } 3 \qquad \textbf{(D) } 4 \qquad \textbf{(E) } ~5</math>
+[[2022 AMC 8 Problems/Problem 5|Solution]]
 ==Problem 6==
-[[2020 AMC 8 Problems/Problem 6|Solution]]
+Three positive integers are equally spaced on a number line. The middle number is <math>15,</math> and the largest number is <math>4</math> times the smallest number. What is the smallest of these three numbers?
+<math>\textbf{(A) } 4 \qquad \textbf{(B) } 5 \qquad \textbf{(C) } 6 \qquad \textbf{(D) } 7 \qquad \textbf{(E) } 8</math>
+[[2022 AMC 8 Problems/Problem 6|Solution]]
 ==Problem 7==
-[[2020 AMC 8 Problems/Problem 7|Solution]]
+When the World Wide Web first became popular in the <math>1990</math>s, download speeds reached a maximum of about <math>56</math> kilobits per second. Approximately how many minutes would the download of a <math>4.2</math>-megabyte song have taken at that speed? (Note that there are <math>8000</math> kilobits in a megabyte.)
+<math>\textbf{(A) } 0.6 \qquad \textbf{(B) } 10 \qquad \textbf{(C) } 1800 \qquad \textbf{(D) } 7200 \qquad \textbf{(E) } 36000</math>
+[[2022 AMC 8 Problems/Problem 7|Solution]]
 ==Problem 8==
-[[2020 AMC 8 Problems/Problem 8|Solution]]
+What is the value of <cmath>\frac{1}{3}\cdot\frac{2}{4}\cdot\frac{3}{5}\cdots\frac{18}{20}\cdot\frac{19}{21}\cdot\frac{20}{22}?</cmath>
+<math>\textbf{(A) } \frac{1}{462} \qquad \textbf{(B) } \frac{1}{231} \qquad \textbf{(C) } \frac{1}{132} \qquad \textbf{(D) } \frac{2}{213} \qquad \textbf{(E) } \frac{1}{22}</math>
+[[2022 AMC 8 Problems/Problem 8|Solution]]
 ==Problem 9==
-[[2020 AMC 8 Problems/Problem 9|Solution]]
+A cup of boiling water (<math>212^{\circ}\text{F}</math>) is placed to cool in a room whose temperature remains constant at <math>68^{\circ}\text{F}</math>. Suppose the difference between the water temperature and the room temperature is halved every <math>5</math> minutes. What is the water temperature, in degrees Fahrenheit, after <math>15</math> minutes?
+<math>\textbf{(A)} ~77\qquad\textbf{(B)} ~86\qquad\textbf{(C)} ~92\qquad\textbf{(D)} ~98\qquad\textbf{(E)} ~104</math>
+[[2022 AMC 8 Problems/Problem 9|Solution]]
 ==Problem 10==
-[[2020 AMC 8 Problems/Problem 10|Solution]]
+One sunny day, Ling decided to take a hike in the mountains. She left her house at <math>8 \, \textsc{am}</math>, drove at a constant speed of <math>45</math> miles per hour, and arrived at the hiking trail at <math>10 \, \textsc{am}</math>. After hiking for <math>3</math> hours, Ling drove home at a constant speed of <math>60</math> miles per hour. Which of the following graphs best illustrates the distance between Ling’s car and her house over the course of her trip?
+<asy>
+unitsize(12);
+usepackage("mathptmx");
+defaultpen(fontsize(8)+linewidth(.7));
+int mod12(int i) {if (i<13) {return i;} else {return i-12;}}
+void drawgraph(pair sh,string lab) {
+for (int i=0;i<11;++i) {
+for (int j=0;j<6;++j) {
+draw(shift(sh+(i,j))*unitsquare,mediumgray);
+}
+}
+draw(shift(sh)*((-1,0)--(11,0)),EndArrow(angle=20,size=8));
+draw(shift(sh)*((0,-1)--(0,6)),EndArrow(angle=20,size=8));
+for (int i=1;i<10;++i) {
+draw(shift(sh)*((i,-.2)--(i,.2)));
+}
+label("8\tiny{\textsc{am}}",sh+(1,-.2),S);
+for (int i=2;i<9;++i) {
+label(string(mod12(i+7)),sh+(i,-.2),S);
+}
+label("4\tiny{\textsc{pm}}",sh+(9,-.2),S);
+for (int i=1;i<6;++i) {
+label(string(30*i),sh+(0,i),2*W);
+}
+draw(rotate(90)*"Distance (miles)",sh+(-2.1,3),fontsize(10));
+label("$\textbf{("+lab+")}$",sh+(-2.1,6.8),fontsize(12));
+}
+drawgraph((0,0),"A");
+drawgraph((15,0),"B");
+drawgraph((0,-10),"C");
+drawgraph((15,-10),"D");
+drawgraph((0,-20),"E");
+dotfactor=6;
+draw((1,0)--(3,3)--(6,3)--(8,0),linewidth(.9));
+dot((1,0)^^(3,3)^^(6,3)^^(8,0));
+pair sh = (15,0);
+draw(shift(sh)*((1,0)--(3,1.5)--(6,1.5)--(8,0)),linewidth(.9));
+dot(sh+(1,0)^^sh+(3,1.5)^^sh+(6,1.5)^^sh+(8,0));
+pair sh = (0,-10);
+draw(shift(sh)*((1,0)--(3,1.5)--(6,1.5)--(7.5,0)),linewidth(.9));
+dot(sh+(1,0)^^sh+(3,1.5)^^sh+(6,1.5)^^sh+(7.5,0));
+pair sh = (15,-10);
+draw(shift(sh)*((1,0)--(3,4)--(6,4)--(9.3,0)),linewidth(.9));
+dot(sh+(1,0)^^sh+(3,4)^^sh+(6,4)^^sh+(9.3,0));
+pair sh = (0,-20);
+draw(shift(sh)*((1,0)--(3,3)--(6,3)--(7.5,0)),linewidth(.9));
+dot(sh+(1,0)^^sh+(3,3)^^sh+(6,3)^^sh+(7.5,0));
+</asy>
+[[2022 AMC 8 Problems/Problem 10|Solution]]
 ==Problem 11==
-[[2020 AMC 8 Problems/Problem 11|Solution]]
+Henry the donkey has a very long piece of pasta. He takes a number of bites of pasta, each time eating <math>3</math> inches of pasta from the middle of one piece. In the end, he has <math>10</math> pieces of pasta whose total length is <math>17</math> inches. How long, in inches, was the piece of pasta he started with?
+<math>\textbf{(A)} ~34\qquad\textbf{(B)} ~38\qquad\textbf{(C)} ~41\qquad\textbf{(D)} ~44\qquad\textbf{(E)} ~47</math>
+[[2022 AMC 8 Problems/Problem 11|Solution]]
 ==Problem 12==
-[[2020 AMC 8 Problems/Problem 12|Solution]]
+The arrows on the two spinners shown below are spun. Let the number <math>N</math>  equal <math>10</math> times the number on Spinner <math>\text{A}</math>, added to the number on Spinner <math>\text{B}</math>. What is the probability that <math>N</math> is a perfect square number?
+<asy>
+//diagram by pog give me 1 billion dollars for this
+size(6cm);
+usepackage("mathptmx");
+filldraw(arc((0,0), r=4, angle1=0, angle2=90)--(0,0)--cycle,mediumgray*0.5+gray*0.5);
+filldraw(arc((0,0), r=4, angle1=90, angle2=180)--(0,0)--cycle,lightgray);
+filldraw(arc((0,0), r=4, angle1=180, angle2=270)--(0,0)--cycle,mediumgray);
+filldraw(arc((0,0), r=4, angle1=270, angle2=360)--(0,0)--cycle,lightgray*0.5+mediumgray*0.5);
+label("$5$", (-1.5,1.7));
+label("$6$", (1.5,1.7));
+label("$7$", (1.5,-1.7));
+label("$8$", (-1.5,-1.7));
+label("Spinner A", (0, -5.5));
+filldraw(arc((12,0), r=4, angle1=0, angle2=90)--(12,0)--cycle,mediumgray*0.5+gray*0.5);
+filldraw(arc((12,0), r=4, angle1=90, angle2=180)--(12,0)--cycle,lightgray);
+filldraw(arc((12,0), r=4, angle1=180, angle2=270)--(12,0)--cycle,mediumgray);
+filldraw(arc((12,0), r=4, angle1=270, angle2=360)--(12,0)--cycle,lightgray*0.5+mediumgray*0.5);
+label("$1$", (10.5,1.7));
+label("$2$", (13.5,1.7));
+label("$3$", (13.5,-1.7));
+label("$4$", (10.5,-1.7));
+label("Spinner B", (12, -5.5));
+</asy>
+<math>\textbf{(A)} ~\dfrac{1}{16}\qquad\textbf{(B)} ~\dfrac{1}{8}\qquad\textbf{(C)} ~\dfrac{1}{4}\qquad\textbf{(D)} ~\dfrac{3}{8}\qquad\textbf{(E)} ~\dfrac{1}{2}</math>
+[[2022 AMC 8 Problems/Problem 12|Solution]]
 ==Problem 13==
-[[2020 AMC 8 Problems/Problem 13|Solution]]
+How many positive integers can fill the blank in the sentence below?
+“One positive integer is _____ more than twice another, and the sum of the two numbers is <math>28</math>.”
+<math>\textbf{(A) } 6 \qquad \textbf{(B) } 7 \qquad \textbf{(C) } 8 \qquad \textbf{(D) } 9 \qquad \textbf{(E) } 10</math>
+[[2022 AMC 8 Problems/Problem 13|Solution]]
 ==Problem 14==
-In how many ways can the letters in BEEKEEPER be rearranged so that two or more Es do not appear together?
+In how many ways can the letters in <math>\textbf{BEEKEEPER}</math> be rearranged so that two or more <math>\textbf{E}</math>s do not appear together?
-<math>\textbf{(A)} ~1\qquad\textbf{(B)} ~4\qquad\textbf{(C)} ~12\qquad\textbf{(D)} ~24\qquad\textbf{(E)} ~120\qquad</math>
+<math>\textbf{(A) } 1 \qquad \textbf{(B) } 4 \qquad \textbf{(C) } 12 \qquad \textbf{(D) } 24 \qquad \textbf{(E) } 120</math>
-[[2020 AMC 8 Problems/Problem 14|Solution]]
+[[2022 AMC 8 Problems/Problem 14|Solution]]
 ==Problem 15==
-[[2020 AMC 8 Problems/Problem 15|Solution]]
+Laszlo went online to shop for black pepper and found thirty different black pepper options varying in weight and price, shown in the scatter plot below. In ounces, what is the weight of the pepper that offers the lowest price per ounce?
+<asy>
+//diagram by pog
+size(5.5cm);
+usepackage("mathptmx");
+defaultpen(mediumgray*0.5+gray*0.5+linewidth(0.63));
+add(grid(6,6));
+label(scale(0.7)*"$1$", (1,-0.3), black);
+label(scale(0.7)*"$2$", (2,-0.3), black);
+label(scale(0.7)*"$3$", (3,-0.3), black);
+label(scale(0.7)*"$4$", (4,-0.3), black);
+label(scale(0.7)*"$5$", (5,-0.3), black);
+label(scale(0.7)*"$1$", (-0.3,1), black);
+label(scale(0.7)*"$2$", (-0.3,2), black);
+label(scale(0.7)*"$3$", (-0.3,3), black);
+label(scale(0.7)*"$4$", (-0.3,4), black);
+label(scale(0.7)*"$5$", (-0.3,5), black);
+label(scale(0.8)*rotate(90)*"Price (dollars)", (-1,3.2), black);
+label(scale(0.8)*"Weight (ounces)", (3.2,-1), black);
+dot((1,1.2),black);
+dot((1,1.7),black);
+dot((1,2),black);
+dot((1,2.8),black);
+dot((1.5,2.1),black);
+dot((1.5,3),black);
+dot((1.5,3.3),black);
+dot((1.5,3.75),black);
+dot((2,2),black);
+dot((2,2.9),black);
+dot((2,3),black);
+dot((2,4),black);
+dot((2,4.35),black);
+dot((2,4.8),black);
+dot((2.5,2.7),black);
+dot((2.5,3.7),black);
+dot((2.5,4.2),black);
+dot((2.5,4.4),black);
+dot((3,2.5),black);
+dot((3,3.4),black);
+dot((3,4.2),black);
+dot((3.5,3.8),black);
+dot((3.5,4.5),black);
+dot((3.5,4.8),black);
+dot((4,3.9),black);
+dot((4,5.1),black);
+dot((4.5,4.75),black);
+dot((4.5,5),black);
+dot((5,4.5),black);
+dot((5,5),black);
+</asy>
+<math>\textbf{(A) }1\qquad\textbf{(B) }2\qquad\textbf{(C) }3\qquad\textbf{(D) }4\qquad\textbf{(E) }5</math>
+[[2022 AMC 8 Problems/Problem 15|Solution]]
 ==Problem 16==
-[[2020 AMC 8 Problems/Problem 16|Solution]]
+Four numbers are written in a row. The average of the first two is <math>21,</math> the average of the middle two is <math>26,</math> and the average of the last two is <math>30.</math> What is the average of the first and last of the numbers?
+<math>\textbf{(A) } 24 \qquad \textbf{(B) } 25 \qquad \textbf{(C) } 26 \qquad \textbf{(D) } 27 \qquad \textbf{(E) } 28</math>
+[[2022 AMC 8 Problems/Problem 16|Solution]]
 ==Problem 17==
-How many factors of <math>2020</math> have more than <math>3</math> factors? (As an example, <math>12</math> has <math>6</math> factors, namely <math>1, 2, 3, 4, 6,</math> and <math>12.</math>)
-<math>\textbf{(A) }6 \qquad \textbf{(B) }7 \qquad \textbf{(C) }8 \qquad \textbf{(D) }9 \qquad \textbf{(E) }10</math>
+If <math>n</math> is an even positive integer, the <math>\emph{double factorial}</math> notation <math>n!!</math> represents the product of all the even integers from <math>2</math> to <math>n</math>. For example, <math>8!! = 2 \cdot 4 \cdot 6 \cdot 8</math>. What is the units digit of the following sum? <cmath>2!! + 4!! + 6!! + \cdots + 2018!! + 2020!! + 2022!!</cmath>
-[[2020 AMC 8 Problems/Problem 17|Solution]]
+<math>\textbf{(A)} ~0\qquad\textbf{(B)} ~2\qquad\textbf{(C)} ~4\qquad\textbf{(D)} ~6\qquad\textbf{(E)} ~8</math>
+[[2022 AMC 8 Problems/Problem 17|Solution]]
 ==Problem 18==
-Rectangle <math>ABCD</math> is inscribed in a semicircle with diameter <math>\overline{FE},</math> as shown in the figure. Let <math>DA=16,</math> and let <math>FD=AE=9.</math> What is the area of <math>ABCD?</math>
+The midpoints of the four sides of a rectangle are <math>(-3,0), (2,0), (5,4),</math> and <math>(0,4).</math> What is the
+area of the rectangle?
+<math>\textbf{(A) } 20 \qquad \textbf{(B) } 25 \qquad \textbf{(C) } 40 \qquad \textbf{(D) } 50 \qquad \textbf{(E) } 80</math>
+[[2022 AMC 8 Problems/Problem 18|Solution]]
+==Problem 19==
+Mr. Ramos gave a test to his class of <math>20</math> students. The dot plot below shows the distribution of test scores.
 <asy>
-// diagram by SirCalcsALot
+//diagram by pog . give me 1,000,000,000 dollars for this diagram
-draw(arc((0,0),17,180,0));
+size(5cm);
-draw((-17,0)--(17,0));
+defaultpen(0.7);
-fill((-8,0)--(-8,15)--(8,15)--(8,0)--cycle, 1.5*grey);
+dot((0.5,1));
-draw((-8,0)--(-8,15)--(8,15)--(8,0)--cycle);
+dot((0.5,1.5));
-dot("$A$",(8,0), 1.25*S);
+dot((1.5,1));
-dot("$B$",(8,15), 1.25*N);
+dot((1.5,1.5));
-dot("$C$",(-8,15), 1.25*N);
+dot((2.5,1));
-dot("$D$",(-8,0), 1.25*S);
+dot((2.5,1.5));
-dot("$E$",(17,0), 1.25*S);
+dot((2.5,2));
-dot("$F$",(-17,0), 1.25*S);
+dot((2.5,2.5));
-label("$16$",(0,0),N);
+dot((3.5,1));
-label("$9$",(12.5,0),N);
+dot((3.5,1.5));
-label("$9$",(-12.5,0),N);
+dot((3.5,2));
+dot((3.5,2.5));
+dot((3.5,3));
+dot((4.5,1));
+dot((4.5,1.5));
+dot((5.5,1));
+dot((5.5,1.5));
+dot((5.5,2));
+dot((6.5,1));
+dot((7.5,1));
+draw((0,0.5)--(8,0.5),linewidth(0.7));
+defaultpen(fontsize(10.5pt));
+label("$65$", (0.5,-0.1));
+label("$70$", (1.5,-0.1));
+label("$75$", (2.5,-0.1));
+label("$80$", (3.5,-0.1));
+label("$85$", (4.5,-0.1));
+label("$90$", (5.5,-0.1));
+label("$95$", (6.5,-0.1));
+label("$100$", (7.5,-0.1));
 </asy>
-<math>\textbf{(A) }240 \qquad \textbf{(B) }248 \qquad \textbf{(C) }256 \qquad \textbf{(D) }264 \qquad \textbf{(E) }272</math>
+Later Mr. Ramos discovered that there was a scoring error on one of the questions. He regraded the tests, awarding some of the students <math>5</math> extra points, which increased the median test score to <math>85</math>. What is the minimum number of students who received extra points?
-[[2020 AMC 8 Problems/Problem 18|Solution]]
+(Note that the <i>median</i> test score equals the average of the <math>2</math> scores in the middle if the <math>20</math> test scores are arranged in increasing order.)
-==Problem 19==
-A number is called flippy if its digits alternate between two distinct digits. For example, <math>2020</math> and <math>37373</math> are flippy, but <math>3883</math> and <math>123123</math> are not. How many five-digit flippy numbers are divisible by <math>15?</math>
-<math>\textbf{(A) }3 \qquad \textbf{(B) }4 \qquad \textbf{(C) }5 \qquad \textbf{(D) }6 \qquad \textbf{(E) }8</math>
+<math>\textbf{(A)} ~2\qquad\textbf{(B)} ~3\qquad\textbf{(C)} ~4\qquad\textbf{(D)} ~5\qquad\textbf{(E)} ~6\qquad</math>
-[[2020 AMC 8 Problems/Problem 19|Solution]]
+[[2022 AMC 8 Problems/Problem 19|Solution]]
 ==Problem 20==
-A scientist walking through a forest recorded as integers the heights of <math>5</math> trees standing in a row. She observed that each tree was either twice as tall or half as tall as the one to its right. Unfortunately some of her data was lost when rain fell on her notebook. Her notes are shown below, with blanks indicating the missing numbers. Based on her observations, the scientist was able to reconstruct the lost data. What was the average height of the trees, in meters?
-<cmath>
+The grid below is to be filled with integers in such a way that the sum of the numbers in each row and the sum of the numbers in each column are the same. Four numbers are missing. The number <math>x</math> in the lower left corner is larger than the other three missing numbers. What is the smallest possible value of <math>x</math>?
-\begingroup
+<asy>
-\setlength{\tabcolsep}{10pt}
+unitsize(0.5cm);
-\renewcommand{\arraystretch}{1.5}
+draw((3,3)--(-3,3));
-\begin{tabular}{|c|c|}
+draw((3,1)--(-3,1));
-\hline Tree 1 & \rule{0.4cm}{0.15mm} meters \\
+draw((3,-3)--(-3,-3));
-Tree 2 & 11 meters \\
+draw((3,-1)--(-3,-1));
-Tree 3 & \rule{0.5cm}{0.15mm} meters \\
+draw((3,3)--(3,-3));
-Tree 4 & \rule{0.5cm}{0.15mm} meters \\
+draw((1,3)--(1,-3));
-Tree 5 & \rule{0.5cm}{0.15mm} meters \\ \hline
+draw((-3,3)--(-3,-3));
-Average height & \rule{0.5cm}{0.15mm}\text{ .}2 meters \\
+draw((-1,3)--(-1,-3));
-\hline
+label((-2,2),"$-2$");
-\end{tabular}
+label((0,2),"$9$");
-\endgroup</cmath>
+label((2,2),"$5$");
-<math>\newline \textbf{(A) }22.2 \qquad \textbf{(B) }24.2 \qquad \textbf{(C) }33.2 \qquad \textbf{(D) }35.2 \qquad \textbf{(E) }37.2</math>
+label((2,0),"${-}1$");
+label((2,-2),"$8$");
+label((-2,-2),"$x$");
+</asy>
+<math>\textbf{(A) } {-}1 \qquad \textbf{(B) } 5 \qquad \textbf{(C) } 6 \qquad \textbf{(D) } 8 \qquad \textbf{(E) } 9</math>
-[[2020 AMC 8 Problems/Problem 20|Solution]]
+[[2022 AMC 8 Problems/Problem 20|Solution]]
 ==Problem 21==
-A game board consists of <math>64</math> squares that alternate in color between black and white. The figure below shows square <math>P</math> in the bottom row and square <math>Q</math> in the top row. A marker is placed at <math>P.</math> A step consists of moving the marker onto one of the adjoining white squares in the row above. How many <math>7</math>-step paths are there from <math>P</math> to <math>Q?</math> (The figure shows a sample path.)
+Steph scored <math>15</math> baskets out of <math>20</math> attempts in the first half of a game, and <math>10</math> baskets out of <math>10</math> attempts in the second half. Candace took <math>12</math> attempts in the first half and <math>18</math> attempts in the second. In each half, Steph scored a higher percentage of baskets than Candace. Surprisingly they ended with the same overall percentage of baskets scored. How many more baskets did Candace score in the second half than in the first?
 <asy>
-// diagram by SirCalcsALot
+size(7cm);
-size(200);
+draw((-8,27)--(72,27));
-int[] x = {6, 5, 4, 5, 6, 5, 6};
+draw((16,0)--(16,35));
-int[] y = {1, 2, 3, 4, 5, 6, 7};
+draw((40,0)--(40,35));
-int N = 7;
+label("12", (28,3));
-for (int i = 0; i < 8; ++i) {
+draw((25,6.5)--(25,12)--(31,12)--(31,6.5)--cycle);
-for (int j = 0; j < 8; ++j) {
+draw((25,5.5)--(31,5.5));
-draw((i,j)--(i+1,j)--(i+1,j+1)--(i,j+1)--(i,j));
+label("18", (56,3));
-if ((i+j) % 2 == 0) {
+draw((53,6.5)--(53,12)--(59,12)--(59,6.5)--cycle);
-filldraw((i,j)--(i+1,j)--(i+1,j+1)--(i,j+1)--(i,j)--cycle,black);
+draw((53,5.5)--(59,5.5));
-}
+draw((53,5.5)--(59,5.5));
-}
+label("20", (28,18));
-}
+label("15", (28,24));
-for (int i = 0; i < N; ++i) {
+draw((25,21)--(31,21));
-draw(circle((x[i],y[i])+(0.5,0.5),0.35),grey);
+label("10", (56,18));
-}
+label("10", (56,24));
-label("$P$", (5.5, 0.5));
+draw((53,21)--(59,21));
-label("$Q$", (6.5, 7.5));
+label("First Half", (28,31));
+label("Second Half", (56,31));
+label("Candace", (2.35,6));
+label("Steph", (0,21));
 </asy>
+<math>\textbf{(A) } 7\qquad\textbf{(B) } 8\qquad\textbf{(C) } 9\qquad\textbf{(D) } 10\qquad\textbf{(E) } 11</math>
-<math>\textbf{(A) }28 \qquad \textbf{(B) }30 \qquad \textbf{(C) }32 \qquad \textbf{(D) }33 \qquad \textbf{(E) }35</math>
+[[2022 AMC 8 Problems/Problem 21|Solution]]
-[[2020 AMC 8 Problems/Problem 21|Solution]]
 ==Problem 22==
-When a positive integer <math>N</math> is fed into a machine, the output is a number calculated according to the rule shown below.
+A bus takes <math>2</math> minutes to drive from one stop to the next, and waits <math>1</math> minute at each stop to let passengers board. Zia takes <math>5</math> minutes to walk from one bus stop to the next. As Zia reaches a bus stop, if the bus is at the previous stop or has already left the previous stop, then she will wait for the bus. Otherwise she will start walking toward the next stop. Suppose the bus and Zia start at the same time toward the library, with the bus <math>3</math> stops behind. After how many minutes will Zia board the bus?
-<asy>
+[[File:2022 AMC 8 Problem 22 Diagram.png|750px|center]]
-size(300);
-defaultpen(linewidth(0.8)+fontsize(13));
-real r = 0.05;
-draw((0.9,0)--(3.5,0),EndArrow(size=7));
-filldraw((4,2.5)--(7,2.5)--(7,-2.5)--(4,-2.5)--cycle,gray(0.65));
-fill(circle((5.5,1.25),0.8),white);
-fill(circle((5.5,1.25),0.5),gray(0.65));
-fill((4.3,-r)--(6.7,-r)--(6.7,-1-r)--(4.3,-1-r)--cycle,white);
-fill((4.3,-1.25+r)--(6.7,-1.25+r)--(6.7,-2.25+r)--(4.3,-2.25+r)--cycle,white);
-fill((4.6,-0.25-r)--(6.4,-0.25-r)--(6.4,-0.75-r)--(4.6,-0.75-r)--cycle,gray(0.65));
-fill((4.6,-1.5+r)--(6.4,-1.5+r)--(6.4,-2+r)--(4.6,-2+r)--cycle,gray(0.65));
-label("$N$",(0.45,0));
-draw((7.5,1.25)--(11.25,1.25),EndArrow(size=7));
-draw((7.5,-1.25)--(11.25,-1.25),EndArrow(size=7));
-label("if $N$ is even",(9.25,1.25),N);
-label("if $N$ is odd",(9.25,-1.25),N);
-label("$\frac N2$",(12,1.25));
-label("$3N+1$",(12.6,-1.25));
-</asy>
-For example, starting with an input of <math>N=7,</math> the machine will output <math>3 \cdot 7 +1 = 22.</math> Then if the output is repeatedly inserted into the machine five more times, the final output is <math>26.</math>
+<math>\textbf{(A) } 17 \qquad \textbf{(B) } 19 \qquad \textbf{(C) } 20 \qquad \textbf{(D) } 21 \qquad \textbf{(E) } 23</math>
-<cmath>7 \to 22 \to 11 \to 34 \to 17 \to 52 \to 26</cmath>When the same <math>6</math>-step process is applied to a different starting value of <math>N,</math> the final output is <math>1.</math> What is the sum of all such integers <math>N?</math>
-<cmath>N \to \rule{0.5cm}{0.15mm} \to \rule{0.5cm}{0.15mm} \to \rule{0.5cm}{0.15mm} \to \rule{0.5cm}{0.15mm} \to \rule{0.5cm}{0.15mm} \to 1</cmath>
-<math>\textbf{(A) }73 \qquad \textbf{(B) }74 \qquad \textbf{(C) }75 \qquad \textbf{(D) }82 \qquad \textbf{(E) }83</math>
+[[2022 AMC 8 Problems/Problem 22|Solution]]
-[[2020 AMC 8 Problems/Problem 22|Solution]]
 ==Problem 23==
-Five different awards are to be given to three students. Each student will receive at least one award. In how many different ways can the awards be distributed?
+A <math>\triangle</math> or <math>\bigcirc</math> is placed in each of the nine squares in a <math>3</math>-by-<math>3</math> grid. Shown below is a sample configuration with three <math>\triangle</math>s in a line.
+<asy>
+//diagram by kante314
+size(3.3cm);
+defaultpen(linewidth(1));
+real r = 0.37;
+path equi = r * dir(-30) -- (r+0.03) * dir(90) -- r * dir(210) -- cycle;
+draw((0,0)--(0,3)--(3,3)--(3,0)--cycle);
+draw((0,1)--(3,1)--(3,2)--(0,2)--cycle);
+draw((1,0)--(1,3)--(2,3)--(2,0)--cycle);
+draw(circle((3/2,5/2),1/3));
+draw(circle((5/2,1/2),1/3));
+draw(circle((3/2,3/2),1/3));
+draw(shift(0.5,0.38) * equi);
+draw(shift(1.5,0.38) * equi);
+draw(shift(0.5,1.38) * equi);
+draw(shift(2.5,1.38) * equi);
+draw(shift(0.5,2.38) * equi);
+draw(shift(2.5,2.38) * equi);
+</asy>
+How many configurations will have three <math>\triangle</math>s in a line and three <math>\bigcirc</math>s in a line?
-<math>\textbf{(A) }120 \qquad \textbf{(B) }150 \qquad \textbf{(C) }180 \qquad \textbf{(D) }210 \qquad \textbf{(E) }240</math>
+<math>\textbf{(A) } 39 \qquad \textbf{(B) } 42 \qquad \textbf{(C) } 78 \qquad \textbf{(D) } 84 \qquad \textbf{(E) } 96</math>
-[[2020 AMC 8 Problems/Problem 23|Solution]]
+[[2022 AMC 8 Problems/Problem 23|Solution]]
 ==Problem 24==
-A large square region is paved with <math>n^2</math> gray square tiles, each measuring <math>s</math> inches on a side. A border <math>d</math> inches wide surrounds each tile. The figure below shows the case for <math>n=3</math>. When <math>n=24</math>
-, the <math>576</math> gray tiles cover <math>64\%</math> of the area of the large square region. What is the ratio <math>\frac{d}{s}</math> for this larger value of <math>n?</math>
+The figure below shows a polygon <math>ABCDEFGH</math>, consisting of rectangles and right triangles. When cut out and folded on the dotted lines, the polygon forms a triangular prism. Suppose that <math>AH = EF = 8</math> and <math>GH = 14</math>. What is the volume of the prism?
 <asy>
-draw((0,0)--(13,0)--(13,13)--(0,13)--cycle);
+usepackage("mathptmx");
-filldraw((1,1)--(4,1)--(4,4)--(1,4)--cycle, mediumgray);
+size(275);
-filldraw((1,5)--(4,5)--(4,8)--(1,8)--cycle, mediumgray);
+defaultpen(linewidth(0.8));
-filldraw((1,9)--(4,9)--(4,12)--(1,12)--cycle, mediumgray);
+real r = 2, s = 2.5, theta = 14;
-filldraw((5,1)--(8,1)--(8,4)--(5,4)--cycle, mediumgray);
+pair G = (0,0), F = (r,0), C = (r,s), B = (0,s), M = (C+F)/2, I = M + s/2 * dir(-theta);
-filldraw((5,5)--(8,5)--(8,8)--(5,8)--cycle, mediumgray);
+pair N = (B+G)/2, J = N + s/2 * dir(180+theta);
-filldraw((5,9)--(8,9)--(8,12)--(5,12)--cycle, mediumgray);
+pair E = F + r * dir(- 45 - theta/2), D = I+E-F;
-filldraw((9,1)--(12,1)--(12,4)--(9,4)--cycle, mediumgray);
+pair H = J + r * dir(135 + theta/2), A = B+H-J;
-filldraw((9,5)--(12,5)--(12,8)--(9,8)--cycle, mediumgray);
+draw(A--B--C--I--D--E--F--G--J--H--cycle^^rightanglemark(F,I,C)^^rightanglemark(G,J,B));
-filldraw((9,9)--(12,9)--(12,12)--(9,12)--cycle, mediumgray);
+draw(J--B--G^^C--F--I,linetype ("4 4"));
+dot("$A$",A,N);
+dot("$B$",B,1.2*N);
+dot("$C$",C,N);
+dot("$D$",D,dir(0));
+dot("$E$",E,S);
+dot("$F$",F,1.5*dir(-100));
+dot("$G$",G,S);
+dot("$H$",H,W);
+dot("$I$",I,NE);
+dot("$J$",J,1.5*S);
 </asy>
-<math>\textbf{(A) }\frac6{25} \qquad \textbf{(B) }\frac14 \qquad \textbf{(C) }\frac9{25} \qquad \textbf{(D) }\frac7{16} \qquad \textbf{(E) }\frac9{16}</math>
+<math>\textbf{(A)} ~112\qquad\textbf{(B)} ~128\qquad\textbf{(C)} ~192\qquad\textbf{(D)} ~240\qquad\textbf{(E)} ~288</math>
-[[2020 AMC 8 Problems/Problem 24|Solution]]
+[[2022 AMC 8 Problems/Problem 24|Solution]]
 ==Problem 25==
-Rectangles <math>R_1</math> and <math>R_2,</math> and squares <math>S_1,\,S_2,\,</math> and <math>S_3,</math> shown below, combine to form a rectangle that is 3322 units wide and 2020 units high. What is the side length of <math>S_2</math> in units?
-<asy>
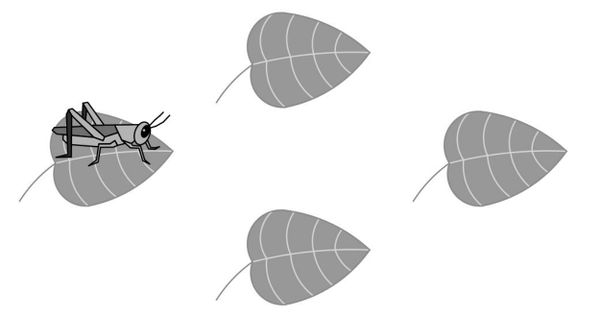
+A cricket randomly hops between <math>4</math> leaves, on each turn hopping to one of the other <math>3</math> leaves with equal probability. After <math>4</math> hops, what is the probability that the cricket has returned to the leaf where it started?
-draw((0,0)--(5,0)--(5,3)--(0,3)--(0,0));
-draw((3,0)--(3,1)--(0,1));
+[[File:2022 AMC 8 Problem 25 Picture.jpg|center|600px]]
-draw((3,1)--(3,2)--(5,2));
-draw((3,2)--(2,2)--(2,1)--(2,3));
+<math>\textbf{(A) }\frac{2}{9}\qquad\textbf{(B) }\frac{19}{80}\qquad\textbf{(C) }\frac{20}{81}\qquad\textbf{(D) }\frac{1}{4}\qquad\textbf{(E) }\frac{7}{27}</math>
-label("$R_1$",(3/2,1/2));
-label("$S_3$",(4,1));
-label("$S_2$",(5/2,3/2));
-label("$S_1$",(1,2));
-label("$R_2$",(7/2,5/2));
-</asy>
-<math>\textbf{(A) }651 \qquad \textbf{(B) }655 \qquad \textbf{(C) }656 \qquad \textbf{(D) }662 \qquad \textbf{(E) }666</math>
+[[2022 AMC 8 Problems/Problem 25|Solution]]
-[[2020 AMC 8 Problems/Problem 25|Solution]]
+==See Also==
+{{AMC8 box|year=2022|before=[[2020 AMC 8 Problems|2020 AMC 8]]|after=[[2023 AMC 8 Problems|2023 AMC 8]]}}
+* [[AMC 8]]
+* [[AMC 8 Problems and Solutions]]
+* [[Mathematics competition resources|Mathematics Competition Resources]]

2022 AMC 8 (Problems • Answer Key • Resources)
Preceded by 2020 AMC 8	Followed by 2023 AMC 8
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AJHSME/AMC 8 Problems and Solutions

Page

Toolbox

Search

Difference between revisions of "2022 AMC 8 Problems"

Latest revision as of 13:53, 6 July 2024

Contents

Problem 1

Problem 2

Problem 3

Problem 4

Problem 5

Problem 6

Problem 7

Problem 8

Problem 9

Problem 10

Problem 11

Problem 12

Problem 13

Problem 14

Problem 15

Problem 16

Problem 17

Problem 18

Problem 19

Problem 20

Problem 21

Problem 22

Problem 23

Problem 24

Problem 25

See Also