Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2021 Fall AMC 10A Problems/Problem 24"

m (→‎Solution 4 (Graph Coloring))
(→‎Case 1)
 
(18 intermediate revisions by 5 users not shown)
Line 5: Line 5:
  
 
==Solution 1==
 
==Solution 1==
−
For simplicity purposes, we name this cube <math>ABCDEFGH</math> by vertices, as shown below.
+
For simplicity, we will name this cube <math>ABCDEFGH</math> by vertices, as shown below.
 
<asy>
 
<asy>
 
/* Made by MRENTHUSIASM */
 
/* Made by MRENTHUSIASM */
Line 32: Line 32:
 
dot("$H$",H,1.5*NW,linewidth(4));
 
dot("$H$",H,1.5*NW,linewidth(4));
 
</asy>
 
</asy>
−
Note that for each face of this cube, two edges are labeled <math>0</math> and two edges are labeled <math>1.</math> For all twelve edges of this cube, we conclude that six edges are labeled <math>0,</math> and six edges are labeled <math>1.</math>
+
Note that for each face of this cube, two edges are labeled <math>0,</math> and two edges are labeled <math>1.</math> For all twelve edges of this cube, we conclude that six edges are labeled <math>0,</math> and six edges are labeled <math>1.</math>
  
 
We apply casework to face <math>ABCD.</math> Recall that there are <math>\binom42=6</math> ways to label its edges:
 
We apply casework to face <math>ABCD.</math> Recall that there are <math>\binom42=6</math> ways to label its edges:
 
<ol style="margin-left: 1.5em;">
 
<ol style="margin-left: 1.5em;">
 
   <li><b>Opposite edges have the same label.</b></li><p>
 
   <li><b>Opposite edges have the same label.</b></li><p>
−
There are <math>2</math> ways to label the edges of <math>ABCD.</math> We will consider one of the ways, then multiply the count by <math>2.</math> Without the loss of generality, we assume that <math>\overline{AB},\overline{BC},\overline{CD},\overline{DA}</math> are labeled <math>1,0,1,0,</math> respectively:<p>
+
There are <math>2</math> ways to label the edges of <math>ABCD.</math> We will consider one of the ways, then multiply the count by <math>2.</math> Without loss of generality, we assume that <math>\overline{AB},\overline{BC},\overline{CD},\overline{DA}</math> are labeled <math>1,0,1,0,</math> respectively:<p>
 
We apply casework to the label of <math>\overline{AE},</math> as shown below.
 
We apply casework to the label of <math>\overline{AE},</math> as shown below.
 
<asy>
 
<asy>
Line 116: Line 116:
 
We have <math>2\cdot2=4</math> such labelings for this case.
 
We have <math>2\cdot2=4</math> such labelings for this case.
 
   <li><b>Opposite edges have different labels.</b></li><p>
 
   <li><b>Opposite edges have different labels.</b></li><p>
−
There are <math>4</math> ways to label the edges of <math>ABCD.</math> We will consider one of the ways, then multiply the count by <math>4.</math> Without the loss of generality, we assume that <math>\overline{AB},\overline{BC},\overline{CD},\overline{DA}</math> are labeled <math>1,1,0,0,</math> respectively:<p>
+
There are <math>4</math> ways to label the edges of <math>ABCD.</math> We will consider one of the ways, then multiply the count by <math>4.</math> Without loss of generality, we assume that <math>\overline{AB},\overline{BC},\overline{CD},\overline{DA}</math> are labeled <math>1,1,0,0,</math> respectively:<p>
 
We apply casework to the labels of <math>\overline{AE}</math> and <math>\overline{BF},</math> as shown below.
 
We apply casework to the labels of <math>\overline{AE}</math> and <math>\overline{BF},</math> as shown below.
 
<asy>
 
<asy>
Line 269: Line 269:
 
Since we want the sum of the edges of each face to be <math>2</math>, we need there to be two <math>1</math>s and two <math>0</math>s on each face. Through experimentation, we find that either <math>2, 4,</math> or all of them have <math>1</math>s adjacent to <math>1</math>s and <math>0</math>s adjacent to <math>0</math> on each face. WLOG, let the first face (counterclockwise) be <math>0,0,1,1</math>. In this case we are trying to have all of them be adjacent to each other. First face: <math>0,0,1,1</math>. Second face: <math>2</math> choices: <math>1,0,0,1</math> or <math>0,0,1,1</math>. After that, it is basically forced and everything will fall in to place. Since we assumed WLOG, we need to multiply <math>2</math> by <math>4</math> to get a total of <math>8</math> different arrangements.  
 
Since we want the sum of the edges of each face to be <math>2</math>, we need there to be two <math>1</math>s and two <math>0</math>s on each face. Through experimentation, we find that either <math>2, 4,</math> or all of them have <math>1</math>s adjacent to <math>1</math>s and <math>0</math>s adjacent to <math>0</math> on each face. WLOG, let the first face (counterclockwise) be <math>0,0,1,1</math>. In this case we are trying to have all of them be adjacent to each other. First face: <math>0,0,1,1</math>. Second face: <math>2</math> choices: <math>1,0,0,1</math> or <math>0,0,1,1</math>. After that, it is basically forced and everything will fall in to place. Since we assumed WLOG, we need to multiply <math>2</math> by <math>4</math> to get a total of <math>8</math> different arrangements.  
  
−
Secondly: <math>4</math> of the faces have all of them adjacent and <math>2</math> of the faces do not: WLOG counting counterclockwise, we have <math>0,0,1,1</math>. Then, we choose the other face next to it. There are two cases, which are <math>0,1,0,1</math> and <math>1,0,1,0</math>. Therefore, this subcase has <math>4</math> different arrangements. Then, we can choose the face at front to be <math>1,0,1,0</math>. This has <math>4</math> cases. The sides can either be <math>0,1,1,0</math> or <math>1,1,0,0</math>. Therefore, we have another <math>8</math> cases.
+
Secondly, <math>4</math> of the faces have all of them adjacent and <math>2</math> of the faces do not: WLOG counting counterclockwise, we have <math>0,0,1,1</math>. Then, we choose the other face next to it. There are two cases, which are <math>0,1,0,1</math> and <math>1,0,1,0</math>. Therefore, this subcase has <math>4</math> different arrangements. Then, we can choose the face at front to be <math>1,0,1,0</math>. This has <math>4</math> cases. The sides can either be <math>0,1,1,0</math> or <math>1,1,0,0</math>. Therefore, we have another <math>8</math> cases.
  
−
Summing these up, we have <math>8+4+8 = 20</math>. Therefore, our answer is <math>\boxed {\textbf{(E) }20}</math>
+
Summing these up, we have <math>8+4+8 = 20</math>. Therefore, our answer is <math>\boxed{\textbf{(E) } 20}</math>.
 +
 
 +
<u><b>Remark</b></u>
 +
 
 +
It is very easy to get disorganized when counting, resulting in incorrect calculations, so when doing this problem, make sure to draw a diagram of the cube. Labeling is a bit harder, since we often confuse one side with another. Try doing the problem by labeling sides on the lines (literally letting the lines pass through your <math>0</math>s and <math>1</math>s.) I found that to be very helpful when solving this problem.
  
 
~Arcticturn
 
~Arcticturn
−
 
−
Remark: It is very easy to get disorganized when counting, so when doing this problem, make sure to draw a diagram of the cube. Labeling is a bit harder, since we often confuse one side with another. Try doing the problem by labeling sides on the lines (literally letting the lines pass through your <math>0</math>s and <math>1</math>s.) I found that to be very helpful when solving this problem.
 
  
 
==Solution 3==
 
==Solution 3==
Line 367: Line 369:
  
 
We can see that we choose <math>2</math> diametrically opposite vertices to put <math>3</math> <math>1</math>'s on the connecting edges. As a result, this case has <math>\frac{8}{2}=4</math> orientations.
 
We can see that we choose <math>2</math> diametrically opposite vertices to put <math>3</math> <math>1</math>'s on the connecting edges. As a result, this case has <math>\frac{8}{2}=4</math> orientations.
 +
 +
An alternate way to count would be to realize that you can rotate the configuration four times yielding four different configurations, but when you reflect horizontally and diagonally, you don't get another unique configuration, rather you get the same configuration as if you rotated it. ~mathboy282
  
 
===Case 2===
 
===Case 2===
Line 698: Line 702:
 
Similarly, if the <math>3</math> edges connecting to <math>A</math> has three <math>0</math>'s, it would be the same as the inverse of case 1, or case 2.2.1, resulting in no new solutions.  
 
Similarly, if the <math>3</math> edges connecting to <math>A</math> has three <math>0</math>'s, it would be the same as the inverse of case 1, or case 2.2.1, resulting in no new solutions.  
  
−
Putting all the cases together, we have <math>4+6+4+6=\boxed {\textbf{(E) }20}</math> solutions.
+
Putting all the cases together, we have <math>4+6+4+6=\boxed{\textbf{(E) } 20}</math> solutions.
  
 
~ConcaveTriangle
 
~ConcaveTriangle
  
−
== Solution 4 (Graph Coloring)==
+
== Solution 4==
  
 
The problem states the sum of the labels on the edges of each of the <math>6</math> faces of the cube equal to <math>2</math>. That is, the sum of the labels on the <math>4</math> edges of a face is equal to <math>2</math>. The labels can only be <math>0</math> or <math>1</math>, meaning <math>2</math> edges are labeled <math>1</math>, the other <math>2</math> are labeled <math>0</math>.
 
The problem states the sum of the labels on the edges of each of the <math>6</math> faces of the cube equal to <math>2</math>. That is, the sum of the labels on the <math>4</math> edges of a face is equal to <math>2</math>. The labels can only be <math>0</math> or <math>1</math>, meaning <math>2</math> edges are labeled <math>1</math>, the other <math>2</math> are labeled <math>0</math>.
  
−
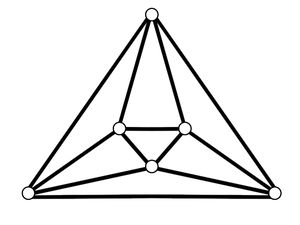
This problem can be approached by [https://en.wikipedia.org/wiki/Graph_coloring Graph Coloring] from [https://en.wikipedia.org/wiki/Graph_theory Graph Theory]. Note that each face of the cube connects to <math>4</math> other faces, each with a shared edge. We use the following graph to represent the problem. Each vertex represents a face, each edge represent the cube's edge. Each vertex has <math>4</math> edges connecting to <math>4</math> other vertices. The edges can be colored red or blue, with red as label <math>0</math>, and blue as label <math>1</math>. Each vertex must have <math>2</math> red edges and <math>2</math> blue edges.
+
This problem can be approached by [https://en.wikipedia.org/wiki/Graph_coloring Graph Coloring] of [https://en.wikipedia.org/wiki/Graph_theory Graph Theory]. Note that each face of the cube connects to <math>4</math> other faces, each with a shared edge. We use the following graph to represent the problem. Each vertex represents a face, each edge represent the cube's edge. Each vertex has <math>4</math> edges connecting to <math>4</math> other vertices. The edges can be colored red or blue, with red as label <math>0</math>, and blue as label <math>1</math>. Each vertex must have <math>2</math> red edges and <math>2</math> blue edges.
 +
 
 +
[[File:Graph coloring normal.jpg|300px|center]]
 +
 
 +
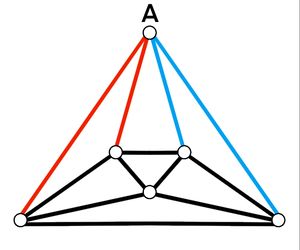
<math>\textbf{Case 1}</math>: <math>2</math> adjacent red edges from vertex A. There are <math>4</math> ways to choose <math>2</math> red edges adjacent to each other and connect to <math>2</math> vertices with an edge between them as shown below.
 +
 
 +
[[File:Graph coloring 1.jpg|300px|center]]
 +
 
 +
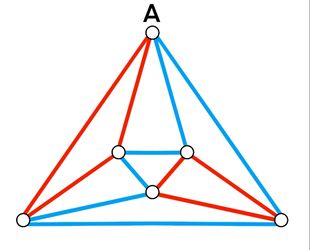
<math>\textbf{Case 1.1}</math>: <math>2</math> adjacent red edges from vertex <math>A</math> form a closed loop with a third red edge. There is only <math>1</math> case as shown below.
 +
 
 +
[[File:Graph coloring case 1.1 .jpg | 310px|center]]
 +
 
 +
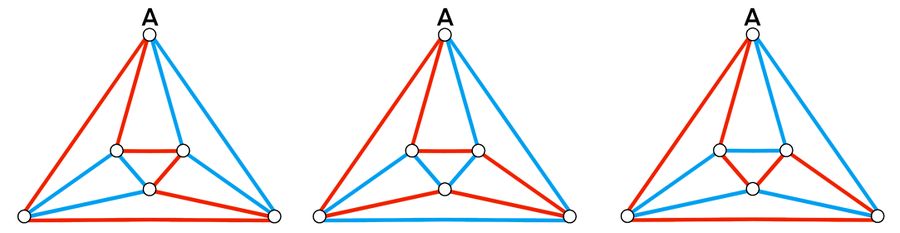
<math>\textbf{Case 1.2}</math>: <math>2</math> adjacent red edges from vertex <math>A</math> does not form a closed loop with a third red edge. There are <math>3</math> cases as shown below.
 +
 
 +
[[File:Graph coloring case 1.2 .jpg | 900px|center]]
 +
 
 +
In case <math>1</math>, there are total <math>4 \cdot (1 + 3) = 16</math> ways.
 +
 
 +
<math>\textbf{Case 2}</math>: <math>2</math> red edges from vertex <math>A</math> with <math>1</math> blue edge in between. There are <math>2</math> ways to choose <math>2</math> red edges with <math>1</math> blue edge in between.
 +
 
 +
[[File:Graph coloring case 2 .jpg | 300px|center]]
 +
 
 +
There are only <math>2</math> cases as shown below.
 +
 
 +
[[File:Graph coloring case 2.1 .jpg | 600px|center]]
 +
 
 +
In case <math>2</math>, there are total <math>2 \cdot 2 = 4</math> ways.
  
−
[[File:Graph coloring normal.jpg|200px]]
+
From both case <math>1</math> and case <math>2</math>, there are <math>16 + 4 = \boxed{\textbf{(E) } 20}</math> ways in total.
  
 
~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]
 
~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]

Latest revision as of 11:13, 13 October 2024

Problem

Each of the $12$ edges of a cube is labeled $0$ or $1$. Two labelings are considered different even if one can be obtained from the other by a sequence of one or more rotations and/or reflections. For how many such labelings is the sum of the labels on the edges of each of the $6$ faces of the cube equal to $2$?

$\textbf{(A) } 8 \qquad\textbf{(B) } 10 \qquad\textbf{(C) } 12 \qquad\textbf{(D) } 16 \qquad\textbf{(E) } 20$

Solution 1

For simplicity, we will name this cube $ABCDEFGH$ by vertices, as shown below. [asy] /* Made by MRENTHUSIASM */ size(150); pair A, B, C, D, E, F, G, H; A = (0,1); B = (1,1); C = (1,0); D = (0,0); E = (0.3,1.3); F = (1.3,1.3); G = (1.3,0.3); H = (0.3,0.3); draw(A--B--C--D--cycle^^A--E^^B--F^^C--G^^E--F--G); draw(H--D^^H--E^^H--G,dashed); dot("$A$",A,1.5*W,linewidth(4)); dot("$B$",B,1.5*(1,0),linewidth(4)); dot("$C$",C,1.5*SE,linewidth(4)); dot("$D$",D,1.5*SW,linewidth(4)); dot("$E$",E,1.5*NW,linewidth(4)); dot("$F$",F,1.5*NE,linewidth(4)); dot("$G$",G,1.5*NE,linewidth(4)); dot("$H$",H,1.5*NW,linewidth(4)); [/asy] Note that for each face of this cube, two edges are labeled $0,$ and two edges are labeled $1.$ For all twelve edges of this cube, we conclude that six edges are labeled $0,$ and six edges are labeled $1.$

We apply casework to face $ABCD.$ Recall that there are $\binom42=6$ ways to label its edges:

  1. Opposite edges have the same label.

    2. There are $2$ ways to label the edges of $ABCD.$ We will consider one of the ways, then multiply the count by $2.$ Without loss of generality, we assume that $\overline{AB},\overline{BC},\overline{CD},\overline{DA}$ are labeled $1,0,1,0,$ respectively:

    We apply casework to the label of $\overline{AE},$ as shown below. [asy] /* Made by MRENTHUSIASM */ size(1200,150); pair A, B, C, D, E, F, G, H, A1, B1, C1, D1, E1, F1, G1, H1, V; A = (0,1); B = (1,1); C = (1,0); D = (0,0); E = (0.3,1.3); F = (1.3,1.3); G = (1.3,0.3); H = (0.3,0.3); V = (3,0); A1 = A+V; B1 = B+V; C1 = C+V; D1 = D+V; E1 = E+V; F1 = F+V; G1 = G+V; H1 = H+V; draw(A--B--C--D--cycle^^A--E^^B--F^^C--G^^E--F--G); draw(H--D^^H--E^^H--G,dashed); draw(A1--B1--C1--D1--cycle^^A1--E1^^B1--F1^^C1--G1^^E1--F1--G1); draw(H1--D1^^H1--E1^^H1--G1,dashed); dot("$A$",A,1.5*W,linewidth(4)); dot("$B$",B,1.5*(1,0),linewidth(4)); dot("$C$",C,1.5*SE,linewidth(4)); dot("$D$",D,1.5*SW,linewidth(4)); dot("$E$",E,1.5*NW,linewidth(4)); dot("$F$",F,1.5*NE,linewidth(4)); dot("$G$",G,1.5*NE,linewidth(4)); dot("$H$",H,1.5*NW,linewidth(4)); dot("$A$",A1,1.5*W,linewidth(4)); dot("$B$",B1,1.5*(1,0),linewidth(4)); dot("$C$",C1,1.5*SE,linewidth(4)); dot("$D$",D1,1.5*SW,linewidth(4)); dot("$E$",E1,1.5*NW,linewidth(4)); dot("$F$",F1,1.5*NE,linewidth(4)); dot("$G$",G1,1.5*NE,linewidth(4)); dot("$H$",H1,1.5*NW,linewidth(4)); label("$1$",midpoint(A--B),red,Fill(1.5,2,white)); label("$0$",midpoint(B--C),red,Fill(1.5,2,white)); label("$1$",midpoint(C--D),red,Fill(1.5,2,white)); label("$0$",midpoint(D--A),red,Fill(1.5,2,white)); label("$1$",midpoint(A1--B1),red,Fill(1.5,2,white)); label("$0$",midpoint(B1--C1),red,Fill(1.5,2,white)); label("$1$",midpoint(C1--D1),red,Fill(1.5,2,white)); label("$0$",midpoint(D1--A1),red,Fill(1.5,2,white)); label("$0$",midpoint(A--E),blue,Fill(1.5,2,white)); label("$1$",midpoint(E--H),blue,Fill(1.5,2,white)); label("$1$",midpoint(H--D),blue,Fill(1.5,2,white)); label("$0$",midpoint(G--C),blue,Fill(1.5,2,white)); label("$0$",midpoint(G--H),blue,Fill(1.5,2,white)); label("$1$",midpoint(B--F),blue,Fill(1.5,2,white)); label("$1$",midpoint(F--G),blue,Fill(1.5,2,white)); label("$0$",midpoint(E--F),blue,Fill(1.5,2,white)); label("$1$",midpoint(A1--E1),blue,Fill(1.5,2,white)); label("$0$",midpoint(E1--F1),blue,Fill(1.5,2,white)); label("$0$",midpoint(B1--F1),blue,Fill(1.5,2,white)); label("$1$",midpoint(F1--G1),blue,Fill(1.5,2,white)); label("$1$",midpoint(G1--C1),blue,Fill(1.5,2,white)); label("$0$",midpoint(G1--H1),blue,Fill(1.5,2,white)); label("$0$",midpoint(H1--D1),blue,Fill(1.5,2,white)); label("$1$",midpoint(E1--H1),blue,Fill(1.5,2,white)); label("The label of $\overline{AE}$ is $0.$",(D.x-0.25,D.y-0.5),blue,align=right); label("The label of $\overline{AE}$ is $1.$",(D1.x-0.25,D1.y-0.5),blue,align=right); [/asy] We have $2\cdot2=4$ such labelings for this case.

  2. Opposite edges have different labels.

    3. There are $4$ ways to label the edges of $ABCD.$ We will consider one of the ways, then multiply the count by $4.$ Without loss of generality, we assume that $\overline{AB},\overline{BC},\overline{CD},\overline{DA}$ are labeled $1,1,0,0,$ respectively:

    We apply casework to the labels of $\overline{AE}$ and $\overline{BF},$ as shown below. [asy] /* Made by MRENTHUSIASM */ size(1200,150); pair A, B, C, D, E, F, G, H, A1, B1, C1, D1, E1, F1, G1, H1, A2, B2, C2, D2, E2, F2, G2, H2, A3, B3, C3, D3, E3, F3, G3, H3, V; A = (0,1); B = (1,1); C = (1,0); D = (0,0); E = (0.3,1.3); F = (1.3,1.3); G = (1.3,0.3); H = (0.3,0.3); V = (3,0); A1 = A+V; B1 = B+V; C1 = C+V; D1 = D+V; E1 = E+V; F1 = F+V; G1 = G+V; H1 = H+V; A2 = A1+V; B2 = B1+V; C2 = C1+V; D2 = D1+V; E2 = E1+V; F2 = F1+V; G2 = G1+V; H2 = H1+V; A3 = A2+V; B3 = B2+V; C3 = C2+V; D3 = D2+V; E3 = E2+V; F3 = F2+V; G3 = G2+V; H3 = H2+V; draw(A--B--C--D--cycle^^A--E^^B--F^^C--G^^E--F--G); draw(H--D^^H--E^^H--G,dashed); draw(A1--B1--C1--D1--cycle^^A1--E1^^B1--F1^^C1--G1^^E1--F1--G1); draw(H1--D1^^H1--E1^^H1--G1,dashed); draw(A2--B2--C2--D2--cycle^^A2--E2^^B2--F2^^C2--G2^^E2--F2--G2); draw(H2--D2^^H2--E2^^H2--G2,dashed); draw(A3--B3--C3--D3--cycle^^A3--E3^^B3--F3^^C3--G3^^E3--F3--G3); draw(H3--D3^^H3--E3^^H3--G3,dashed); dot("$A$",A,W,linewidth(4)); dot("$B$",B,(1,0),linewidth(4)); dot("$C$",C,SE,linewidth(4)); dot("$D$",D,SW,linewidth(4)); dot("$E$",E,NW,linewidth(4)); dot("$F$",F,NE,linewidth(4)); dot("$G$",G,NE,linewidth(4)); dot("$H$",H,NW,linewidth(4)); dot("$A$",A1,W,linewidth(4)); dot("$B$",B1,(1,0),linewidth(4)); dot("$C$",C1,SE,linewidth(4)); dot("$D$",D1,SW,linewidth(4)); dot("$E$",E1,NW,linewidth(4)); dot("$F$",F1,NE,linewidth(4)); dot("$G$",G1,NE,linewidth(4)); dot("$H$",H1,NW,linewidth(4)); dot("$A$",A2,W,linewidth(4)); dot("$B$",B2,(1,0),linewidth(4)); dot("$C$",C2,SE,linewidth(4)); dot("$D$",D2,SW,linewidth(4)); dot("$E$",E2,NW,linewidth(4)); dot("$F$",F2,NE,linewidth(4)); dot("$G$",G2,NE,linewidth(4)); dot("$H$",H2,NW,linewidth(4)); dot("$A$",A3,W,linewidth(4)); dot("$B$",B3,(1,0),linewidth(4)); dot("$C$",C3,SE,linewidth(4)); dot("$D$",D3,SW,linewidth(4)); dot("$E$",E3,NW,linewidth(4)); dot("$F$",F3,NE,linewidth(4)); dot("$G$",G3,NE,linewidth(4)); dot("$H$",H3,NW,linewidth(4)); label("$1$",midpoint(A--B),red,Fill(1.5,2,white)); label("$1$",midpoint(B--C),red,Fill(1.5,2,white)); label("$0$",midpoint(C--D),red,Fill(1.5,2,white)); label("$0$",midpoint(D--A),red,Fill(1.5,2,white)); label("$1$",midpoint(A1--B1),red,Fill(1.5,2,white)); label("$1$",midpoint(B1--C1),red,Fill(1.5,2,white)); label("$0$",midpoint(C1--D1),red,Fill(1.5,2,white)); label("$0$",midpoint(D1--A1),red,Fill(1.5,2,white)); label("$1$",midpoint(A2--B2),red,Fill(1.5,2,white)); label("$1$",midpoint(B2--C2),red,Fill(1.5,2,white)); label("$0$",midpoint(C2--D2),red,Fill(1.5,2,white)); label("$0$",midpoint(D2--A2),red,Fill(1.5,2,white)); label("$1$",midpoint(A3--B3),red,Fill(1.5,2,white)); label("$1$",midpoint(B3--C3),red,Fill(1.5,2,white)); label("$0$",midpoint(C3--D3),red,Fill(1.5,2,white)); label("$0$",midpoint(D3--A3),red,Fill(1.5,2,white)); label("$0$",midpoint(A--E),blue,Fill(0,0,white)); label("$0$",midpoint(B--F),blue,Fill(0,0,white)); label("$1$",midpoint(E--F),blue,Fill(1.5,2,white)); label("$1$",midpoint(E--H),blue,Fill(1.5,2,white)); label("$1$",midpoint(D--H),blue,Fill(0,0,white)); label("$0$",midpoint(F--G),blue,Fill(1.5,2,white)); label("$0$",midpoint(G--H),blue,Fill(1.5,2,white)); label("$1$",midpoint(G--C),blue,Fill(0,0,white)); label("$0$",midpoint(A1--E1),blue,Fill(0,0,white)); label("$1$",midpoint(B1--F1),blue,Fill(0,0,white)); label("$0$",midpoint(E1--F1),blue,Fill(1.5,2,white)); label("$1$",midpoint(E1--H1),blue,Fill(1.5,2,white)); label("$1$",midpoint(D1--H1),blue,Fill(0,0,white)); label("$0$",midpoint(F1--G1),blue,Fill(1.5,2,white)); label("$1$",midpoint(G1--H1),blue,Fill(1.5,2,white)); label("$0$",midpoint(G1--C1),blue,Fill(0,0,white)); label("$1$",midpoint(A2--E2),blue,Fill(0,0,white)); label("$0$",midpoint(B2--F2),blue,Fill(0,0,white)); label("$0$",midpoint(E2--F2),blue,Fill(1.5,2,white)); label("$1$",midpoint(E2--H2),blue,Fill(1.5,2,white)); label("$0$",midpoint(D2--H2),blue,Fill(0,0,white)); label("$0$",midpoint(F2--G2),blue,Fill(1.5,2,white)); label("$1$",midpoint(G2--H2),blue,Fill(1.5,2,white)); label("$1$",midpoint(G2--C2),blue,Fill(0,0,white)); label("$1$",midpoint(A3--E3),blue,Fill(0,0,white)); label("$0$",midpoint(B3--F3),blue,Fill(0,0,white)); label("$0$",midpoint(E3--F3),blue,Fill(1.5,2,white)); label("$0$",midpoint(E3--H3),blue,Fill(1.5,2,white)); label("$1$",midpoint(D3--H3),blue,Fill(0,0,white)); label("$1$",midpoint(F3--G3),blue,Fill(1.5,2,white)); label("$1$",midpoint(G3--H3),blue,Fill(1.5,2,white)); label("$0$",midpoint(G3--C3),blue,Fill(0,0,white)); label("The label of $\overline{AE}$ is $0.$",(D.x-0.25,D.y-0.5),blue,align=right); label("The label of $\overline{BF}$ is $0.$",(D.x-0.25,D.y-0.75),blue,align=right); label("The label of $\overline{AE}$ is $0.$",(D1.x-0.25,D1.y-0.5),blue,align=right); label("The label of $\overline{BF}$ is $1.$",(D1.x-0.25,D1.y-0.75),blue,align=right); draw(brace((G3.x+0.25,-0.5),(D2.x-0.25,-0.5),.3),blue); label("The label of $\overline{AE}$ is $1.$",(G2.x-0.25,D2.y-1),blue,align=right); label("The label of $\overline{BF}$ is $0.$",(G2.x-0.25,D2.y-1.25),blue,align=right); [/asy] We have $4\cdot4=16$ such labelings for this case.

Therefore, we have $4+16=\boxed{\textbf{(E) } 20}$ such labelings in total.

~MRENTHUSIASM

Solution 2

Since we want the sum of the edges of each face to be $2$, we need there to be two $1$s and two $0$s on each face. Through experimentation, we find that either $2, 4,$ or all of them have $1$s adjacent to $1$s and $0$s adjacent to $0$ on each face. WLOG, let the first face (counterclockwise) be $0,0,1,1$. In this case we are trying to have all of them be adjacent to each other. First face: $0,0,1,1$. Second face: $2$ choices: $1,0,0,1$ or $0,0,1,1$. After that, it is basically forced and everything will fall in to place. Since we assumed WLOG, we need to multiply $2$ by $4$ to get a total of $8$ different arrangements.

Secondly, $4$ of the faces have all of them adjacent and $2$ of the faces do not: WLOG counting counterclockwise, we have $0,0,1,1$. Then, we choose the other face next to it. There are two cases, which are $0,1,0,1$ and $1,0,1,0$. Therefore, this subcase has $4$ different arrangements. Then, we can choose the face at front to be $1,0,1,0$. This has $4$ cases. The sides can either be $0,1,1,0$ or $1,1,0,0$. Therefore, we have another $8$ cases.

Summing these up, we have $8+4+8 = 20$. Therefore, our answer is $\boxed{\textbf{(E) } 20}$.

Remark

It is very easy to get disorganized when counting, resulting in incorrect calculations, so when doing this problem, make sure to draw a diagram of the cube. Labeling is a bit harder, since we often confuse one side with another. Try doing the problem by labeling sides on the lines (literally letting the lines pass through your $0$s and $1$s.) I found that to be very helpful when solving this problem.

~Arcticturn

Solution 3

[asy] pair A, B, C, D, E, F, G, H; A = (0, 0); B = (12.071,0); C = (12.071,12.071); D = (0,12.071); E = (3.536,3.536); F = (8.536,3.536); G = (8.536,8.536); H = (3.536,8.536); draw(A--B--C--D--A--E--F--G--H--E--F--B--C--G--H--D); label("$A$", A, SW); label("$B$", B, SE); label("$C$", C, NE); label("$D$", D, NW); label("$E$", E, NW); label("$F$", F, NE); label("$G$", G, SE); label("$H$", H, SW); [/asy]

We see that each face has to have 2 1's and 2 0's. We can start with edges connecting to A.

Case 1

[asy] pair A, B, C, D, E, F, G, H; A = (0, 0); B = (12.071,0); C = (12.071,12.071); D = (0,12.071); E = (3.536,3.536); F = (8.536,3.536); G = (8.536,8.536); H = (3.536,8.536); draw(A--B--C--D--A--E--F--G--H--E--F--B--C--G--H--D); label("$A$", A, SW); label("$B$", B, SE); label("$C$", C, NE); label("$D$", D, NW); label("$E$", E, NW); label("$F$", F, NE); label("$G$", G, SE); label("$H$", H, SW); label("$1$", A--B, S); label("$1$", A--D, W); label("$1$", A--E, NW); [/asy]

This goes to:

[asy] pair A, B, C, D, E, F, G, H; A = (0, 0); B = (12.071,0); C = (12.071,12.071); D = (0,12.071); E = (3.536,3.536); F = (8.536,3.536); G = (8.536,8.536); H = (3.536,8.536); draw(A--B--C--D--A--E--F--G--H--E--F--B--C--G--H--D); label("$A$", A, SW); label("$B$", B, SE); label("$C$", C, NE); label("$D$", D, NW); label("$E$", E, NW); label("$F$", F, NE); label("$G$", G, SE); label("$H$", H, SW); label("$1$", A--B, S); label("$0$", B--C, (1,0)); label("$0$", C--D, N); label("$1$", D--A, W); label("$0$", E--F, S); label("$1$", F--G, (1,0)); label("$1$", G--H, N); label("$0$", H--E, W); label("$1$", A--E, NW); label("$0$", B--F, NE); label("$1$", C--G, SE); label("$0$", D--H, SW); [/asy]

We can see that we choose $2$ diametrically opposite vertices to put $3$ $1$'s on the connecting edges. As a result, this case has $\frac{8}{2}=4$ orientations.

An alternate way to count would be to realize that you can rotate the configuration four times yielding four different configurations, but when you reflect horizontally and diagonally, you don't get another unique configuration, rather you get the same configuration as if you rotated it. ~mathboy282

Case 2

[asy] pair A, B, C, D, E, F, G, H; A = (0, 0); B = (12.071,0); C = (12.071,12.071); D = (0,12.071); E = (3.536,3.536); F = (8.536,3.536); G = (8.536,8.536); H = (3.536,8.536); draw(A--B--C--D--A--E--F--G--H--E--F--B--C--G--H--D); label("$A$", A, SW); label("$B$", B, SE); label("$C$", C, NE); label("$D$", D, NW); label("$E$", E, NW); label("$F$", F, NE); label("$G$", G, SE); label("$H$", H, SW); label("$0$", A--B, S); label("$1$", A--D, W); label("$1$", A--E, NW); [/asy]

Filling out a bit more, we have:

[asy] pair A, B, C, D, E, F, G, H; A = (0, 0); B = (12.071,0); C = (12.071,12.071); D = (0,12.071); E = (3.536,3.536); F = (8.536,3.536); G = (8.536,8.536); H = (3.536,8.536); draw(A--B--C--D--A--E--F--G--H--E--F--B--C--G--H--D); label("$A$", A, SW); label("$B$", B, SE); label("$C$", C, NE); label("$D$", D, NW); label("$E$", E, NW); label("$F$", F, NE); label("$G$", G, SE); label("$H$", H, SW); label("$0$", A--B, S); label("$1$", A--D, W); label("$1$", A--E, NW); label("$0$", H--E, W); label("$0$", D--H, SW); [/asy]

Let's try filling out $BC$ and $CD$ first.

Case 2.1

[asy] pair A, B, C, D, E, F, G, H; A = (0, 0); B = (12.071,0); C = (12.071,12.071); D = (0,12.071); E = (3.536,3.536); F = (8.536,3.536); G = (8.536,8.536); H = (3.536,8.536); draw(A--B--C--D--A--E--F--G--H--E--F--B--C--G--H--D); label("$A$", A, SW); label("$B$", B, SE); label("$C$", C, NE); label("$D$", D, NW); label("$E$", E, NW); label("$F$", F, NE); label("$G$", G, SE); label("$H$", H, SW); label("$0$", A--B, S); label("$$", B--C, (1,0)); label("$$", C--D, N); label("$1$", D--A, W); label("$0$", E--F, S); label("$$", F--G, (1,0)); label("$$", G--H, N); label("$0$", H--E, W); label("$1$", A--E, NW); label("$1$", B--F, NE); label("$$", C--G, SE); label("$0$", D--H, SW); [/asy]

This goes to:

[asy] pair A, B, C, D, E, F, G, H; A = (0, 0); B = (12.071,0); C = (12.071,12.071); D = (0,12.071); E = (3.536,3.536); F = (8.536,3.536); G = (8.536,8.536); H = (3.536,8.536); draw(A--B--C--D--A--E--F--G--H--E--F--B--C--G--H--D); label("$A$", A, SW); label("$B$", B, SE); label("$C$", C, NE); label("$D$", D, NW); label("$E$", E, NW); label("$F$", F, NE); label("$G$", G, SE); label("$H$", H, SW); label("$0$", A--B, S); label("$0$", B--C, (1,0)); label("$1$", C--D, N); label("$1$", D--A, W); label("$0$", E--F, S); label("$1$", F--G, (1,0)); label("$1$", G--H, N); label("$0$", H--E, W); label("$1$", A--E, NW); label("$1$", B--F, NE); label("$0$", C--G, SE); label("$0$", D--H, SW); [/asy]

We can see that it consists of chains of three $1$'s, with the middle of each chain being opposite edges. As a result, this case has $\frac{12}{2}=6$ orientations.

Case 2.2

[asy] pair A, B, C, D, E, F, G, H; A = (0, 0); B = (12.071,0); C = (12.071,12.071); D = (0,12.071); E = (3.536,3.536); F = (8.536,3.536); G = (8.536,8.536); H = (3.536,8.536); draw(A--B--C--D--A--E--F--G--H--E--F--B--C--G--H--D); label("$A$", A, SW); label("$B$", B, SE); label("$C$", C, NE); label("$D$", D, NW); label("$E$", E, NW); label("$F$", F, NE); label("$G$", G, SE); label("$H$", H, SW); label("$0$", A--B, S); label("$$", B--C, (1,0)); label("$$", C--D, N); label("$1$", D--A, W); label("$1$", E--F, S); label("$$", F--G, (1,0)); label("$$", G--H, N); label("$0$", H--E, W); label("$1$", A--E, NW); label("$0$", B--F, NE); label("$$", C--G, SE); label("$0$", D--H, SW); [/asy]

Oh no... We have different ways of filling out $FG$ and $GH$. More casework!

Case 2.2.1

[asy] pair A, B, C, D, E, F, G, H; A = (0, 0); B = (12.071,0); C = (12.071,12.071); D = (0,12.071); E = (3.536,3.536); F = (8.536,3.536); G = (8.536,8.536); H = (3.536,8.536); draw(A--B--C--D--A--E--F--G--H--E--F--B--C--G--H--D); label("$A$", A, SW); label("$B$", B, SE); label("$C$", C, NE); label("$D$", D, NW); label("$E$", E, NW); label("$F$", F, NE); label("$G$", G, SE); label("$H$", H, SW); label("$0$", A--B, S); label("$$", B--C, (1,0)); label("$$", C--D, N); label("$1$", D--A, W); label("$1$", E--F, S); label("$1$", F--G, (1,0)); label("$0$", G--H, N); label("$0$", H--E, W); label("$1$", A--E, NW); label("$0$", B--F, NE); label("$$", C--G, SE); label("$0$", D--H, SW); [/asy]

This goes to:

[asy] pair A, B, C, D, E, F, G, H; A = (0, 0); B = (12.071,0); C = (12.071,12.071); D = (0,12.071); E = (3.536,3.536); F = (8.536,3.536); G = (8.536,8.536); H = (3.536,8.536); draw(A--B--C--D--A--E--F--G--H--E--F--B--C--G--H--D); label("$A$", A, SW); label("$B$", B, SE); label("$C$", C, NE); label("$D$", D, NW); label("$E$", E, NW); label("$F$", F, NE); label("$G$", G, SE); label("$H$", H, SW); label("$0$", A--B, S); label("$0$", B--C, (1,0)); label("$1$", C--D, N); label("$1$", D--A, W); label("$1$", E--F, S); label("$1$", F--G, (1,0)); label("$0$", G--H, N); label("$0$", H--E, W); label("$1$", A--E, NW); label("$0$", B--F, NE); label("$1$", C--G, SE); label("$0$", D--H, SW); [/asy]

We can see that this is the inverse of case 1 (Define inverse to mean swapping $1$'s for $0$'s and $0$'s for $1$'s). Therefore, this should also have $4$ orientations.

Case 2.2.2

[asy] pair A, B, C, D, E, F, G, H; A = (0, 0); B = (12.071,0); C = (12.071,12.071); D = (0,12.071); E = (3.536,3.536); F = (8.536,3.536); G = (8.536,8.536); H = (3.536,8.536); draw(A--B--C--D--A--E--F--G--H--E--F--B--C--G--H--D); label("$A$", A, SW); label("$B$", B, SE); label("$C$", C, NE); label("$D$", D, NW); label("$E$", E, NW); label("$F$", F, NE); label("$G$", G, SE); label("$H$", H, SW); label("$0$", A--B, S); label("$$", B--C, (1,0)); label("$$", C--D, N); label("$1$", D--A, W); label("$1$", E--F, S); label("$0$", F--G, (1,0)); label("$1$", G--H, N); label("$0$", H--E, W); label("$1$", A--E, NW); label("$0$", B--F, NE); label("$$", C--G, SE); label("$0$", D--H, SW); [/asy]

This goes to:

[asy] pair A, B, C, D, E, F, G, H; A = (0, 0); B = (12.071,0); C = (12.071,12.071); D = (0,12.071); E = (3.536,3.536); F = (8.536,3.536); G = (8.536,8.536); H = (3.536,8.536); draw(A--B--C--D--A--E--F--G--H--E--F--B--C--G--H--D); label("$A$", A, SW); label("$B$", B, SE); label("$C$", C, NE); label("$D$", D, NW); label("$E$", E, NW); label("$F$", F, NE); label("$G$", G, SE); label("$H$", H, SW); label("$0$", A--B, S); label("$1$", B--C, (1,0)); label("$0$", C--D, N); label("$1$", D--A, W); label("$1$", E--F, S); label("$0$", F--G, (1,0)); label("$1$", G--H, N); label("$0$", H--E, W); label("$1$", A--E, NW); label("$0$", B--F, NE); label("$1$", C--G, SE); label("$0$", D--H, SW); [/asy]

This is the inverse of case 2.1, so this will also have $6$ orientations.

Putting Them All Together

We see that if the $3$ edges connecting to $A$ has two $0$'s, and one $1$, it would have the same solutions as if it had two $1$'s, and one $0$. The solutions would just be inverted. As case 2.1 and case 2.2.2 are inverses, and case 2.2.1 has case 1 as an inverse, there would not be any additional solutions.

Similarly, if the $3$ edges connecting to $A$ has three $0$'s, it would be the same as the inverse of case 1, or case 2.2.1, resulting in no new solutions.

Putting all the cases together, we have $4+6+4+6=\boxed{\textbf{(E) } 20}$ solutions.

~ConcaveTriangle

Solution 4

The problem states the sum of the labels on the edges of each of the $6$ faces of the cube equal to $2$. That is, the sum of the labels on the $4$ edges of a face is equal to $2$. The labels can only be $0$ or $1$, meaning $2$ edges are labeled $1$, the other $2$ are labeled $0$.

This problem can be approached by Graph Coloring of Graph Theory. Note that each face of the cube connects to $4$ other faces, each with a shared edge. We use the following graph to represent the problem. Each vertex represents a face, each edge represent the cube's edge. Each vertex has $4$ edges connecting to $4$ other vertices. The edges can be colored red or blue, with red as label $0$, and blue as label $1$. Each vertex must have $2$ red edges and $2$ blue edges.

Graph coloring normal.jpg

$\textbf{Case 1}$: $2$ adjacent red edges from vertex A. There are $4$ ways to choose $2$ red edges adjacent to each other and connect to $2$ vertices with an edge between them as shown below.

Graph coloring 1.jpg

$\textbf{Case 1.1}$: $2$ adjacent red edges from vertex $A$ form a closed loop with a third red edge. There is only $1$ case as shown below.

Graph coloring case 1.1 .jpg

$\textbf{Case 1.2}$: $2$ adjacent red edges from vertex $A$ does not form a closed loop with a third red edge. There are $3$ cases as shown below.

Graph coloring case 1.2 .jpg

In case $1$, there are total $4 \cdot (1 + 3) = 16$ ways.

$\textbf{Case 2}$: $2$ red edges from vertex $A$ with $1$ blue edge in between. There are $2$ ways to choose $2$ red edges with $1$ blue edge in between.

Graph coloring case 2 .jpg

There are only $2$ cases as shown below.

Graph coloring case 2.1 .jpg

In case $2$, there are total $2 \cdot 2 = 4$ ways.

From both case $1$ and case $2$, there are $16 + 4 = \boxed{\textbf{(E) } 20}$ ways in total.

~isabelchen

See Also

2021 Fall AMC 10A (Problems • Answer Key • Resources)
Preceded by
Problem 23 		Followed by
Problem 25
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2021_Fall_AMC_10A_Problems/Problem_24&oldid=229726"