Difference between revisions of "2021 Fall AMC 10B Problems/Problem 15"

Latest revision as of 16:33, 6 June 2024

1 Problem
2 Solution 1
3 Solution 2 (Similarity, Pythagorean Theorem, and Systems of Equations)
4 Solution 3
5 Solution 4 (Point-line distance formula)
6 Solution 5
7 Solution 6 (Answer choices and areas)
8 Solution 7 (Power of a Point)
9 Video Solution by Interstigation
10 Video Solution
11 Video Solution by WhyMath
12 Video Solution by TheBeautyofMath
13 Video Solution by OmegaLearn
14 See Also

Problem

In square $ABCD$ , points $P$ and $Q$ lie on $\overline{AD}$ and $\overline{AB}$ , respectively. Segments $\overline{BP}$ and $\overline{CQ}$ intersect at right angles at $R$ , with $BR = 6$ and $PR = 7$ . What is the area of the square?

$[asy] size(170); defaultpen(linewidth(0.6)+fontsize(10)); real r = 3.5; pair A = origin, B = (5,0), C = (5,5), D = (0,5), P = (0,r), Q = (5-r,0), R = intersectionpoint(B--P,C--Q); draw(A--B--C--D--A^^B--P^^C--Q^^rightanglemark(P,R,C,7)); dot("$A$",A,S); dot("$B$",B,S); dot("$C$",C,N); dot("$D$",D,N); dot("$Q$",Q,S); dot("$P$",P,W); dot("$R$",R,1.3*S); label("$7$",(P+R)/2,NE); label("$6$",(R+B)/2,NE); [/asy]$

$\textbf{(A) }85\qquad\textbf{(B) }93\qquad\textbf{(C) }100\qquad\textbf{(D) }117\qquad\textbf{(E) }125$

Solution 1

Note that $\triangle APB \cong \triangle BQC$ by ASA. ( $\angle PAB = \angle QBC = 90^\circ, AB=CB,$ and $\angle PBA = \angle QCB.$ ) Then, it follows that $\overline{PB} \cong \overline{QC}.$ Thus, $QC = PB = PR + RB = 7 + 6 = 13.$ Define $x$ to be the length of side $CR,$ then $RQ = 13-x.$ Because $\overline{BR}$ is the altitude of the triangle, we can use the property that $QR \cdot RC = BR^2.$ Substituting the given lengths, we have $(13-x) \cdot x = 36.$ Solving, gives $RQ = 4$ and $RC = 9.$ We eliminate the possibility of $x=4$ because $RC > QR.$ Thus, the side length of the square, by Pythagorean Theorem, is $\sqrt{9^2 +6^2} = \sqrt{81+36} = \sqrt{117}.$ Thus, the area of the square is $(\sqrt{117})^2 = 117,$ so the answer is $\boxed{\textbf{(D) }117}.$

Note that there is another way to prove that $CR = 4$ is impossible. If $CR = 4,$ then the side length would be $\sqrt{4^2 + 6^2} = \sqrt{52},$ and the area would be $52,$ but that isn't in the answer choices. Thus, $CR$ must be $9.$

~NH14 ~sl_hc

Extra Note: Another way to prove $4$ is impossible. The side length of the square, $S$ , is equal to $\sqrt{4^2 + 6^2} = \sqrt{52}$ . Because $x = 4$ , $RQ = 9$ . Because $QB = \sqrt{RB^2 + RQ^2} = \sqrt{6^2 + 9^2} = \sqrt{117}$ and $QB < S$ but $\sqrt{117} > \sqrt{52}$ , we have proof by contradiction. And so $x = 9$ .

~ Wiselion (Extra Note)

Solution 2 (Similarity, Pythagorean Theorem, and Systems of Equations)

As above, note that $\bigtriangleup BPA \cong \bigtriangleup CQB$ , which means that $QC = 13$ . In addition, note that $BR$ is the altitude of a right triangle to its hypotenuse, so $\bigtriangleup BQR \sim \bigtriangleup CBR \sim \bigtriangleup CQB$ . Let the side length of the square be $x$ ; using similarity side ratios of $\bigtriangleup BQR$ to $\bigtriangleup CQB$ , we get $\frac{6}{x} = \frac{QB}{13} \implies QB \cdot x = 78$ Note that $QB^2 + x^2 = 13^2 = 169$ by the Pythagorean theorem, so we can use the expansion $(a+b)^2 = a^2+2ab+b^2$ to produce two equations and two variables;

$(QB + x)^2 = QB^2 + 2QB\cdot x + x^2 \implies (QB+x)^2 = 169 + 2 \cdot 78 \implies QB+x = \sqrt{13(13)+13(12)} = \sqrt{13 \cdot 25} = 5\sqrt{13}$ $(QB-x)^2 = QB^2 - 2QB\cdot x + x^2 \implies (QB - x)^2 = 169 - 2\cdot 78 \implies \pm(QB-x) = \sqrt{13(13) - 13(12)}$

Since $QB-x$ is negative, it doesn't make sense in the context of this problem, so we go with $x-QB = \sqrt{13(13) - 13(12)} = \sqrt{13 \cdot 1} = \sqrt{13}$

We want $x^2$ , so we want to find $x$ . Adding the first equation to the second, we get $2x = 6\sqrt{13} \implies x = 3\sqrt{13}$

Then $x^2$ = $(3\sqrt{13}^2) = 9 \cdot 13 = 117 = \boxed{D}$

~KingRavi

~stjwyl (Edits)

-yingkai_0_ (Minor Edits)

Solution 3

We have that $\triangle CRB \sim \triangle BAP.$ Thus, $\frac{\overline{CB}}{\overline{CR}} = \frac{\overline{PB}}{\overline{AB}}$ . Now, let the side length of the square be $s.$ Then, by the Pythagorean theorem, $CR = \sqrt{x^2-36}.$ Plugging all of this information in, we get $\frac{s}{\sqrt{s^2-36}} = \frac{13}{s}.$ Simplifying gives $s^2=13\sqrt{s^2-36},$ Squaring both sides gives $s^4 = 169s^2- 169\cdot 36 \implies s^4-169s^2 + 169\cdot 36 = 0.$ We now set $s^2=t,$ and get the equation $t^2-169t + 169\cdot 36 = 0.$ From here, notice we want to solve for $t$ , as it is precisely $s^2,$ or the area of the square. So we use the Quadratic formula, and though it may seem bashy, we hope for a nice cancellation of terms. $t = \frac{169\pm\sqrt{169^2-4\cdot 36 \cdot 169}}{2}.$ It seems scary, but factoring $169$ from the square root gives us $t = \frac{169\pm \sqrt{169 \cdot (169-144)}}{2} = \frac{169 \pm \sqrt{169 \cdot 25}}{2} = \frac{169 \pm 13\cdot 5}{2} = \frac{169\pm 65}{2},$ giving us the solutions $t=52, 117.$ We instantly see that $t=52$ is way too small to be an area of this square ( $52$ isn't even an answer choice, so you can skip this step if out of time) because then the side length would be $2\sqrt{13}$ and then, even the largest line you can draw inside the square (the diagonal) is $2\sqrt{26},$ which is less than $13$ (line $PB$ ) And thus, $t$ must be $117$ , and our answer is $\boxed{\textbf{(D)}}.$ $\blacksquare$

~wamofan

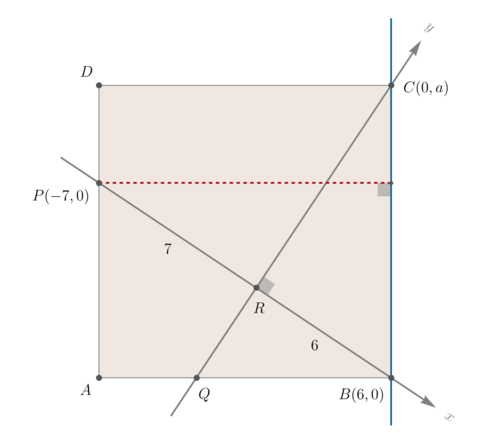
Solution 4 (Point-line distance formula)

Denote $a = RC$ . Now tilt your head to the right and view $R, \overrightarrow{RB}$ and $\overrightarrow{RC}$ as the origin, $x$ -axis and $y$ -axis, respectively. In particular, we have points $B(6,0), C(0,a), P(-7,0)$ . Note that side length of the square $ABCD$ is $BC = \sqrt{a^2 + 36}$ . Also equation of line $BC$ is $\underbrace{\frac{x}{6} + \frac{y}{a} = 1}_{\text{intercepts form}} \quad \implies \quad ax + 6y - 6a = 0.$ Because the distance from $P(-7,0)$ to line $\color[rgb]{0,0.4,0.65}BC: ax + 6y - 6a = 0$ is also the side length $\sqrt{a^2 + 36}$ , we can apply the point-line distance formula to get $\frac{|a\cdot(-7) + 6 \cdot 0 - 6a|}{\sqrt{a^2 + 36}} = {\sqrt{a^2 + 36}}$ which reduces to $|13a| = a^2 + 36$ . Since $a$ is positive, the last equations factors as $a^2 - 13a + 36 = (a-4)(a-9) = 0$ . Now judging from the figure, we learn that $a > RB = 6$ . So $a = 9$ . Therefore, the area of the square $ABCD$ is $BC^2 = RC^2 + RB^2 = a^2 + 6^2 = \boxed{\textbf{(D)}\ 117}$ .

~VensL. can someone explain how line bc doesnt have an undefined slope?? how are there 2 different x coordinates if its a vertical line... ~THATONEKID_-TOKYT- The line is not vertical. Looking closely, you can actually see that CQ and PB lie on the Y and X axis respectively.

Solution 5

Denote $\angle PBA = \alpha$ . Because $\angle QRB = \angle QBC = 90^\circ$ , $\angle BCQ = \alpha$ .

Hence, $AB = BP \cos \angle PBA = 13 \cos \alpha$ , $BC = \frac{BR}{\sin \angle BCQ} = \frac{6}{\sin \alpha}$ .

Because $ABCD$ is a square, $AB = BC$ . Hence, $13 \cos \alpha = \frac{6}{\sin \alpha}$ .

Therefore, $\begin{align*} \sin 2 \alpha & = 2 \sin \alpha \cos \alpha \\ & = \frac{12}{13} . \end{align*}$

Thus, $\cos 2 \alpha = \pm \frac{5}{13}$ .

$\textbf{Case 1}$ : $\cos 2 \alpha = \frac{5}{13}$ .

Thus, $\cos \alpha = \sqrt{\frac{1 + \cos 2 \alpha}{2}} = \frac{3}{\sqrt{13}}$ .

Hence, $AB = 13 \cos \alpha = 3 \sqrt{13}$ .

Therefore, ${\rm Area} \ ABCD = AB^2 = 117$ .

$\textbf{Case 2}$ : $\cos 2 \alpha = - \frac{5}{13}$ .

Thus, $\cos \alpha = \sqrt{\frac{1 + \cos 2 \alpha}{2}} = \frac{2}{\sqrt{13}}$ .

Hence, $AB = 13 \cos \alpha = 2 \sqrt{13}$ .

However, we observe $BQ = \frac{BR}{\cos \alpha} = 3 \sqrt{13} > AB$ . Therefore, in this case, point $Q$ is not on the segment $AB$ .

Therefore, this case is infeasible.

Putting all cases together, the answer is $\boxed{\textbf{(D) }117}$ .

~Steven Chen (www.professorchenedu.com)

Solution 6 (Answer choices and areas)

Note that if we connect points $P$ and $C$ , we get a triangle with height $RC$ and length $13$ . This triangle has an area of $\frac {1}{2}$ the square. We can now use answer choices to our advantage!

Answer choice A: If $BC$ was $\sqrt {85}$ , $RC$ would be $7$ . The triangle would therefore have an area of $\frac {91}{2}$ which is not half of the area of the square. Therefore, A is wrong.

Answer choice B: If $BC$ was $\sqrt {93}$ , $RC$ would be $\sqrt {57}$ . This is obviously wrong.

Answer choice C: If $BC$ was $10$ , we would have that $RC$ is $8$ . The area of the triangle would be $52$ , which is not half the area of the square. Therefore, C is wrong.

Answer choice D: If $BC$ was $\sqrt {117}$ , that would mean that $RC$ is $9$ . The area of the triangle would therefore be $\frac {117}{2}$ which IS half the area of the square. Therefore, our answer is $\boxed {\textbf{(D) 117}}$ .

~Arcticturn

Solution 7 (Power of a Point)

Note that $PRQA$ is a cyclic quadrilateral (opposite angles add to $180^{\circ}$ ). Call the circumcircle of quadrilateral $PRQA$ $O$ . Then the power of $B$ to $O$ is $6\cdot (6+7)=78$ . Let $a$ be the length of $BQ$ and $s$ the side length of the square, then we have $a\cdot s = 78$ , and we also have $a^2 + s^2=13^2$ , solving the two equation will give us $s^2=117$ .

~student99

~minor edits by Yiyj1

Video Solution by Interstigation

https://www.youtube.com/watch?v=sKC0Yt6sPi0

Video Solution

https://youtu.be/_6o7d9pGJng

~Education, the Study of Everything

Video Solution by WhyMath

https://youtu.be/p9Hq6N-cEAM

~savannahsolver

Video Solution by TheBeautyofMath

https://youtu.be/R7TwXgAGYuw?t=1367 (note in the comments an easier solution too from a viewer)

~IceMatrix

Video Solution by OmegaLearn

https://youtu.be/hDsoyvFWYxc?t=822

~ pi_is_3.14

2021 Fall AMC 10B (Problems • Answer Key • Resources)
Preceded by Problem 14	Followed by Problem 16
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

Page

Toolbox

Search