Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1989 AIME Problems/Problem 15"

(→‎Solution 5(Mass of a point+ Stewart+heron))
(→‎Solution 2 (Mass Points, Stewart's Theorem, Heron's Formula))
 
(28 intermediate revisions by 10 users not shown)
Line 3: Line 3:
 
[[Image:AIME_1989_Problem_15.png|center]]
 
[[Image:AIME_1989_Problem_15.png|center]]
  
−
== Solution ==
+
== Solutions ==
−
=== Solution 1 ===
+
 
 +
=== Solution 1 (Ceva's Theorem, Stewart's Theorem) ===
 +
 
 +
Let <math>[RST]</math> be the area of polygon <math>RST</math>.  We'll make use of the following fact: if <math>P</math> is a point in the interior of triangle <math>XYZ</math>, and line <math>XP</math> intersects line <math>YZ</math> at point <math>L</math>, then <math>\dfrac{XP}{PL} = \frac{[XPY] + [ZPX]}{[YPZ]}.</math>
 +
 
 +
<center><asy>
 +
size(170);
 +
pair X = (1,2), Y = (0,0), Z = (3,0);
 +
real x = 0.4, y = 0.2, z = 1-x-y;
 +
pair P = x*X + y*Y + z*Z;
 +
pair L = y/(y+z)*Y + z/(y+z)*Z;
 +
draw(X--Y--Z--cycle);
 +
draw(X--P);
 +
draw(P--L, dotted);
 +
draw(Y--P--Z);
 +
label("$X$", X, N);
 +
label("$Y$", Y, S);
 +
label("$Z$", Z, S);
 +
label("$P$", P, NE);
 +
label("$L$", L, S);</asy></center>
 +
 
 +
This is true because triangles <math>XPY</math> and <math>YPL</math> have their areas in ratio <math>XP:PL</math> (as they share a common height from <math>Y</math>), and the same is true of triangles <math>ZPY</math> and <math>LPZ</math>.
 +
 
 +
We'll also use the related fact that <math>\dfrac{[XPY]}{[ZPX]} = \dfrac{YL}{LZ}</math>.  This is slightly more well known, as it is used in the standard proof of [[Ceva's theorem]].
 +
 
 +
Now we'll apply these results to the problem at hand.
 +
 
 +
<center><asy>
 +
size(170);
 +
pair C = (1, 3), A = (0,0), B = (1.7,0);
 +
real a = 0.5, b= 0.25, c = 0.25;
 +
pair P = a*A + b*B + c*C;
 +
pair D = b/(b+c)*B + c/(b+c)*C;
 +
pair EE = c/(c+a)*C + a/(c+a)*A;
 +
pair F = a/(a+b)*A + b/(a+b)*B;
 +
draw(A--B--C--cycle);
 +
draw(A--P);
 +
draw(B--P--C);
 +
draw(P--D, dotted);
 +
draw(EE--P--F, dotted);
 +
label("$A$", A, S);
 +
label("$B$", B, S);
 +
label("$C$", C, N);
 +
label("$D$", D, NE);
 +
label("$E$", EE, NW);
 +
label("$F$", F, S);
 +
label("$P$", P, E);
 +
</asy></center>
 +
 
 +
Since <math>AP = PD = 6</math>, this means that <math>[APB] + [APC] = [BPC]</math>; thus <math>\triangle BPC</math> has half the area of <math>\triangle ABC</math>.  And since <math>PE = 3 = \dfrac{1}{3}BP</math>, we can conclude that <math>\triangle APC</math> has one third of the combined areas of triangle <math>BPC</math> and <math>APB</math>, and thus <math>\dfrac{1}{4}</math> of the area of <math>\triangle ABC</math>.  This means that <math>\triangle APB</math> is left with <math>\dfrac{1}{4}</math> of the area of triangle <math>ABC</math>:
 +
<cmath> [BPC]: [APC]: [APB] = 2:1:1.</cmath>
 +
Since <math>[APC] = [APB]</math>, and since <math>\dfrac{[APC]}{[APB]} = \dfrac{CD}{DB}</math>, this means that <math>D</math> is the midpoint of <math>BC</math>.
 +
 
 +
Furthermore, we know that <math>\dfrac{CP}{PF} = \dfrac{[APC] + [BPC]}{[APB]} = 3</math>, so <math>CP = \dfrac{3}{4} \cdot CF = 15</math>.
 +
 
 +
We now apply [[Stewart's theorem]] to segment <math>PD</math> in <math>\triangle BPC</math>&mdash;or rather, the simplified version for a median.  This tells us that
 +
<cmath> 2 BD^2 + 2 PD^2 = BP^2+ CP^2. </cmath> Plugging in we know, we learn that
 +
<cmath> \begin{align*}
 +
2 BD^2 + 2 \cdot 36 &= 81 + 225 = 306, \\
 +
BD^2 &= 117. \end{align*} </cmath>
 +
Happily, <math>BP^2 + PD^2 = 81 + 36</math> is also equal to 117.  Therefore <math>\triangle BPD</math> is a right triangle with a right angle at <math>B</math>; its area is thus <math>\dfrac{1}{2} \cdot 9 \cdot 6 = 27</math>.  As <math>PD</math> is a median of <math>\triangle BPC</math>, the area of <math>BPC</math> is twice this, or 54.  And we already know that <math>\triangle BPC</math> has half the area of <math>\triangle ABC</math>, which must therefore be <math>\boxed{108}</math>.
 +
 
 +
=== Solution 2 (Mass Points, Stewart's Theorem, Heron's Formula) ===
 
Because we're given three concurrent [[cevian]]s and their lengths, it seems very tempting to apply [[Mass points]]. We immediately see that <math>w_E = 3</math>, <math>w_B = 1</math>, and <math>w_A = w_D = 2</math>. Now, we recall that the masses on the three sides of the triangle must be balanced out, so <math>w_C = 1</math> and <math>w_F = 3</math>. Thus, <math>CP = 15</math> and <math>PF = 5</math>.  
 
Because we're given three concurrent [[cevian]]s and their lengths, it seems very tempting to apply [[Mass points]]. We immediately see that <math>w_E = 3</math>, <math>w_B = 1</math>, and <math>w_A = w_D = 2</math>. Now, we recall that the masses on the three sides of the triangle must be balanced out, so <math>w_C = 1</math> and <math>w_F = 3</math>. Thus, <math>CP = 15</math> and <math>PF = 5</math>.  
  
−
Recalling that <math>w_C = w_B = 1</math>, we see that <math>DC = DB</math> and <math>DP</math> is a [[median]] to <math>BC</math> in <math>\triangle BCP</math>. Applying [[Stewart's Theorem]], <math>BC^2 + 12^2 = 2(15^2 + 9^2)</math>, and <math>BC = 6\sqrt {13}</math>. Now notice that <math>2[BCP] = [ABC]</math>, because both triangles share the same base and the <math>h_{\triangle ABC} = 2h_{\triangle BCP}</math>. Applying [[Heron's formula]] on triangle <math>BCP</math> with sides <math>15</math>, <math>9</math>, and <math>6\sqrt{13}</math>, <math>[BCP] = 54</math> and <math>[ABC] = \boxed{108}</math>.
+
Recalling that <math>w_C = w_B = 1</math>, we see that <math>DC = DB</math> and <math>DP</math> is a [[median]] to <math>BC</math> in <math>\triangle BCP</math>. Applying [[Stewart's Theorem]], we have the following:
 +
<cmath>\frac{BC}{2}(9^2+15^2)=BC(6^2+ \left(\frac{BC}{2} \right)^2).</cmath>
 +
Eliminating <math>BC</math> on both sides, we have:
 +
<cmath>\frac 12(9^2+15^2)=6^2+ \left(\frac{BC}{2} \right)^2.</cmath>
 +
Combining terms and simplifying numbers, we have:
 +
<cmath>153=36+\left(\frac{BC}{2} \right)^2.</cmath>
 +
Subtracting 36 to the other side yields:
 +
<cmath>117= \left(\frac{BC}{2} \right)^2.</cmath>
 +
Finishing it off from there, we find that <math>BC=2 \sqrt{117}.</math> Now, notice that <math>2[BCP] = [ABC]</math>, because both triangles share the same base, <math>BC</math> and <math>h_{\triangle ABC} = 2h_{\triangle BCP}</math>. Applying [[Heron's formula]] on triangle <math>BCP</math> with sides <math>15</math>, <math>9</math>, and <math>2\sqrt{117}</math>, we have:
 +
<cmath>\sqrt{(\sqrt{117}+12)(\sqrt{117}+12-9)(\sqrt{117}+12-15)(\sqrt{117}+12-2\sqrt{117})}.</cmath>
 +
Combining terms results in:
 +
<cmath>\sqrt{(\sqrt{117}+12)(\sqrt{117}+3)(\sqrt{117}-3)(-\sqrt{117}+12)}.</cmath>
 +
Notice that these factors can be grouped into a difference of squares:
 +
<cmath>\sqrt{(144-\sqrt{117}^2)(\sqrt{117}^2-9)}.</cmath>
 +
Since <math>\sqrt{117}^2=117</math>, we have:
 +
<cmath>\sqrt{(27)(108)}.</cmath>
 +
After simplifying this radical, we find that it equals <math>54.</math> Therefore, <math>[BCP] = 54</math>, and hence <math>[ABC]=2 \cdot 54= \boxed{108}</math>.
  
−
=== Solution 2 ===
+
(The original author made a mistake in their solution. Corrected and further explained by dbnl.)
 +
 
 +
=== Solution 3 (Ceva's Theorem, Stewart's Theorem) ===
 
Using a different form of [[Ceva's Theorem]], we have <math>\frac {y}{x + y} + \frac {6}{6 + 6} + \frac {3}{3 + 9} = 1\Longleftrightarrow\frac {y}{x + y} = \frac {1}{4}</math>
 
Using a different form of [[Ceva's Theorem]], we have <math>\frac {y}{x + y} + \frac {6}{6 + 6} + \frac {3}{3 + 9} = 1\Longleftrightarrow\frac {y}{x + y} = \frac {1}{4}</math>
  
Line 24: Line 104:
 
Using area ratio, <math>\triangle ABC = \triangle ADB\times 2 = \left(\triangle ADQ\times \frac32\right)\times 2 = 36\cdot 3 = \boxed{108}</math>.
 
Using area ratio, <math>\triangle ABC = \triangle ADB\times 2 = \left(\triangle ADQ\times \frac32\right)\times 2 = 36\cdot 3 = \boxed{108}</math>.
  
−
=== Solution 3 ===
+
=== Solution 4 (Stewart's Theorem) ===
−
Because the length of cevian <math>BE</math> is unknown, we can examine what happens when we extend it or decrease its length and see that it simply changes the angles between the cevians. Wouldn't it be great if it the length of <math>BE</math> was such that <math>\angle APC = 90^\circ</math>?  Let's first assume it's a right angle and hope that everything works out.  
+
 
 +
First, let <math>[AEP]=a, [AFP]=b,</math> and <math>[ECP]=c.</math> Thus, we can easily find that <math>\frac{[AEP]}{[BPD]}=\frac{3}{9}=\frac{1}{3} \Leftrightarrow [BPD]=3[AEP]=3a.</math> Now, <math>\frac{[ABP]}{[BPD]}=\frac{6}{6}=1\Leftrightarrow [ABP]=3a.</math> In the same manner, we find that <math>[CPD]=a+c.</math> Now, we can find that <math>\frac{[BPC]}{[PEC]}=\frac{9}{3}=3 \Leftrightarrow \frac{(3a)+(a+c)}{c}=3 \Leftrightarrow c=2a.</math> We can now use this to find that <math>\frac{[APC]}{[AFP]}=\frac{[BPC]}{[BFP]}=\frac{PC}{FP} \Leftrightarrow \frac{3a}{b}=\frac{6a}{3a-b} \Leftrightarrow a=b.</math> Plugging this value in, we find that <math>\frac{FC}{FP}=3 \Leftrightarrow PC=15, FP=5.</math> Now, since <math>\frac{[AEP]}{[PEC]}=\frac{a}{2a}=\frac{1}{2},</math> we can find that <math>2AE=EC.</math> Setting <math>AC=b,</math> we can apply [[Stewart's Theorem]] on triangle <math>APC</math> to find that <math>(15)(15)(\frac{b}{3})+(6)(6)(\frac{2b}{3})=(\frac{2b}{3})(\frac{b}{3})(b)+(b)(3)(3).</math> Solving, we find that <math>b=\sqrt{405} \Leftrightarrow AE=\frac{b}{3}=\sqrt{45}.</math> But, <math>3^2+6^2=45,</math> meaning that <math>\angle{APE}=90 \Leftrightarrow [APE]=\frac{(6)(3)}{2}=9=a.</math> Since <math>[ABC]=a+a+2a+2a+3a+3a=12a=(12)(9)=108,</math> we conclude that the answer is <math>\boxed{108}</math>.
 +
 
 +
=== Solution 5 (Mass of a Point, Stewart's Theorem, Heron's Formula) ===
 +
Firstly, since they all meet at one single point, denoting the mass of them separately. Assuming <math>M(A)=6;M(D)=6;M(B)=3;M(E)=9</math>; we can get that <math>M(P)=12;M(F)=9;M(C)=3</math>; which leads to the ratio between segments,
 +
<cmath>\frac{CE}{AE}=2;\frac{BF}{AF}=2;\frac{BD}{CD}=1.</cmath> Denoting that <math>CE=2x;AE=x; AF=y; BF=2y; CD=z; DB=z.</math>
 +
 
 +
Now we know three cevians' length, Applying Stewart theorem to them, getting three different equations:
 +
<cmath>\begin{align}
 +
(3x)^2 \cdot 2y+(2z)^2 \cdot y&=(3y)(2y^2+400), \\
 +
(3y)^2 \cdot z+(3x)^2 \cdot z&=(2z)(z^2+144), \\
 +
(2z)^2 \cdot x+(3y)^2 \cdot x&=(3x)(2x^2+144).
 +
\end{align}</cmath>
 +
After solving the system of equation, we get that <math>x=3\sqrt{5};y=\sqrt{13};z=3\sqrt{13}</math>;
 +
 
 +
pulling <math>x,y,z</math> back to get the length of <math>AC=9\sqrt{5};AB=3\sqrt{13};BC=6\sqrt{13}</math>; now we can apply Heron's formula here, which is <cmath>\sqrt\frac{(9\sqrt{5}+9\sqrt{13})(9\sqrt{13}-9\sqrt{5})(9\sqrt{5}+3\sqrt{13})(9\sqrt{5}-3\sqrt{13})}{16}=108.</cmath>
 +
 
 +
Our answer is <math>\boxed{108}</math>.
 +
 
 +
~bluesoul
 +
 
 +
====Note (how to find x and y without the system of equations)====
 +
To ease computation, we can apply Stewart's Theorem to find <math>x</math>, <math>y</math>, and <math>z</math> directly. Since <math>M(C)=3</math> and <math>M(F)=9</math>, <math>\overline{PC}=15</math> and <math>\overline{PF}=5</math>. We can apply Stewart's Theorem on <math>\triangle CPE</math> to get <math>(2x+x)(2x \cdot x) + 3^2 \cdot 3x = 15^2 \cdot x + 6^2\cdot 2x</math>. Solving, we find that <math>x=3\sqrt{5}</math>. We can do the same on <math>\triangle APB</math> and <math>\triangle BPC</math> to obtain <math>y</math> and <math>z</math>. We proceed with Heron's Formula as the solution states.
 +
 
 +
~kn07
 +
 
 +
=== Solution 6 (easier version of Solution 5)===
  
−
Extend <math>AD</math> to <math>Q</math> so that <math>PD = DQ = 6</math>. The result is that <math>BQ = 9</math>, <math>PQ = 12</math>, and <math>BP = 15</math> because <math>\triangle CDP\cong \triangle BDQ</math>. Now we see that if we are able to show that <math>BE = 20</math>, that is <math>PE = 5</math>, then our right angle assumption will be true.
+
In Solution 5, instead of finding all of <math>x, y, z</math>, we only need <math>y, z</math>. This is because after we solve for <math>y, z</math>, we can notice that <math>\triangle BAD</math> is isosceles with <math>AB = BD</math>. Because <math>P</math> is the midpoint of the base, <math>BP</math> is an altitude of <math>\triangle BAD</math>. Therefore, <math>[BAD] = \frac{(AD)(BP)}{2} = \frac{12 \cdot 9}{2} = 54</math>. Using the same altitude property, we can find that <math>[ABC] = 2[BAD] = 2 \cdot 54 = \boxed{108}</math>.
  
−
Apply the [[Pythagorean Theorem]] on <math>\triangle APC</math> to get <math>AC = 3\sqrt {13}</math>, so <math>AE = \sqrt {13}</math> and <math>CE = 2\sqrt {13}</math>. Now, we apply the [[Law of Cosines]] on triangles <math>CEP</math> and <math>AEP</math>. 
+
-NL008
  
−
Let <math>PE = x</math>. Notice that <math>\angle CEB = 180^\circ - \angle AEB</math> and <math>\cos CEB = - \cos AEB</math>, so we get two nice equations.
+
=== Solution 7 (Mass Points, Stewart's Theorem, Simple Version) ===
  
−
<math>81 = 52 + y^2 - 2y \sqrt {13}\cos CEF</math>
+
Set <math>AF=x,</math> and use [[mass points]] to find that <math>PF=5</math> and <math>BF=2x.</math> Using [[Stewart's Theorem]] on <math>APB,</math> we find that <math>AB=3\sqrt{13}.</math> Then we notice that <math>APB</math> is right, which means the area of <math>APB</math> is <math>27.</math> Because <math>CF=4\cdot PF,</math> the area of <math>ABC</math> is <math>4</math> times the area of <math>APB,</math> which means the area of <math>ABC=4\cdot 27=\boxed{108}.</math>
−
<math>36 = 13 + y^2 + y \sqrt {13} \cos CEF</math>
 
  
−
Solving, <math>y = 5</math> (yay!).
+
=== Solution 8 (Ratios, Auxiliary Lines and 3-4-5 triangle) ===
  
−
Now, the area is easy to find. <math>[ABC] = [AQB] + [APC] = \frac12(9)(18) + \frac12(6)(9) = \boxed{108}</math>.
+
We try to solve this using only elementary concepts. Let the areas of triangles <math>BCP</math>, <math>ACP</math> and <math>ABP</math> be <math>X</math>, <math>Y</math> and <math>Z</math> respectively. Then <math>\frac{X}{Y+Z}=\frac{6}{6}=1</math> and <math>\frac{Y}{X+Z}=\frac{3}{9}=\frac{1}{3}</math>. Hence <math>\frac{X}{2}=Y=Z</math>. Similarly <math>\frac{FP}{PC}=\frac{Z}{X+Y}=\frac{1}{3}</math> and since <math>CF=20</math> we then have <math>FP=5</math>. Additionally we now see that triangles <math>FPE</math> and <math>CPB</math> are similar, so <math>FE \parallel BC</math> and <math>\frac{FE}{BC} = \frac{1}{3}</math>. Hence <math>\frac{AF}{FB}=\frac{1}{2}</math>. Now construct a point <math>K</math> on segment <math>BP</math> such that <math>BK=6</math> and <math>KP=3</math>, we will have <math>FK \parallel AP</math>, and hence <math>\frac{FK}{AP} = \frac{FK}{6} = \frac{2}{3}</math>, giving <math>FK=4</math>. Triangle <math>FKP</math> is therefore a 3-4-5 triangle! So <math>FK \perp BE</math> and so <math>AP \perp BE</math>. Then it is easy to calculate that <math>Z = \frac{1}{2} \times 6 \times 9 = 27</math> and the area of triangle <math>ABC = X+Y+Z = 4Z = 4 \times 27 = \boxed{108}</math>.
 +
~Leole
  
−
[however, I think this solution is wrong, the A, B, and Cs do not match with the picture]
 
  
−
=== Solution 4 ===
+
=== Solution 9 (Just Trig Bash) ===
  
−
First, let <math>[AEP]=a, [AFP]=b,</math> and <math>[ECP]=c.</math> Thus, we can easily find that <math>\frac{[AEP]}{[BPD]}=\frac{3}{9}=\frac{1}{3} \Leftrightarrow [BPD]=3[AEP]=3a.</math> Now, <math>\frac{[ABP]}{[BPD]}=\frac{6}{6}=1\Leftrightarrow [ABP]=3a.</math> In the same manner, we find that <math>[CPD]=a+c.</math> Now, we can find that <math>\frac{[BPC]}{[PEC]}=\frac{9}{3}=3 \Leftrightarrow \frac{(3a)+(a+c)}{c}=3 \Leftrightarrow c=2a.</math> We can now use this to find that <math>\frac{[APC]}{[AFP]}=\frac{[BPC]}{[BFP]}=\frac{PC}{FP} \Leftrightarrow \frac{3a}{b}=\frac{6a}{3a-b} \Leftrightarrow a=b.</math> Plugging this value in, we find that <math>\frac{FC}{FP}=3 \Leftrightarrow PC=15, FP=5.</math> Now, since <math>\frac{[AEP]}{[PEC]}=\frac{a}{2a}=\frac{1}{2},</math> we can find that <math>2AE=EC.</math> Setting <math>AC=b,</math> we can apply Stewart's Theorem on triangle <math>APC</math> to find that <math>(15)(15)(\frac{b}{3})+(6)(6)(\frac{2b}{3})=(\frac{2b}{3})(\frac{b}{3})(b)+(b)(3)(3).</math> Solving, we find that <math>b=\sqrt{405} \Leftrightarrow AE=\frac{b}{3}=\sqrt{45}.</math> But, <math>3^2+6^2=45,</math> meaning that <math>\angle{APE}=90 \Leftrightarrow [APE]=\frac{(6)(3)}{2}=9=a.</math> Since <math>[ABC]=a+a+2a+2a+3a+3a=12a=(12)(9)=108,</math> we conclude that the answer is <math>\boxed{108}</math>.
+
We start with mass points as in Solution 2, and receive <math>BF:AF = 2</math>, <math>BD:CD = 1</math>, <math>CE:AE = 2</math>. [[Law of Cosines]] on triangles <math>ADB</math> and <math>ADC</math> with <math>\theta = \angle ADB</math> and <math>BD=DC=x</math> gives
−
=== Solution 5(Mass of a point+ Stewart+heron) ===
+
<cmath>36+x^2-12x\cos \theta = 81</cmath>
−
Firstly, since they all meet at one single point, denoting the mass of them separately. Assuming <math>M(A)=6;M(D)=6;M(B)=3;M(E)=9</math>; we can get that <math>M(P)=12;M(F)=9;M(C)=3</math>; which leads to the ratio between segments, <math>\frac{CE}{AE}=2;\frac{BF}{AF}=2;\frac{BD}{CD}=1</math>. Denoting that <math>CE=2x;AE=x; AF=y; BF=2y; CD=z; DB=z.</math>
+
<cmath>36+x^2-12x\cos (180-\theta) = 36+x^2+12x\cos \theta = 225</cmath>
−
Now we know three cevians' length, Applying Stewart theorem to them, getting three different equations:
+
Adding them: <math>72+2x^2=306 \implies x=3\sqrt{13}</math>, so <math>BC = 6\sqrt{13}</math>. Similarly, <math>AB = 3\sqrt{13}</math> and <math>AC = 9\sqrt{5}</math>. Using Heron's,
−
<math>(1): (3x)^2 * 2y+(2z)^2 * y=(3y)(2y^2+400)\\
+
<cmath>[ \triangle ABC ]= \sqrt{\left(\dfrac{9\sqrt{13}+9\sqrt{5}}{2}\right)\left(\dfrac{9\sqrt{13}09\sqrt{5}}{2}\right)\left(\dfrac{3\sqrt{13}+9\sqrt{5}}{2}\right)\left(\dfrac{-3\sqrt{13}+9\sqrt{5}}{2}\right)} = \boxed{108}.</cmath>
−
(2): (3x)^2 * 2y+(2z)^2 * y=(3y)(2y^2+400)\\
+
 
−
(3): (2z)^2 * x+(3y)^2 * x=(3x)(2x^2+144)</math>
+
~sml1809
−
After solving the system of equation, we get that <math>x=3\sqrt{5};y=\sqrt{13};z=3\sqrt{13}</math>;
 
−
pulling <math>x,y,z</math> back to get the length of <math>AC=9\sqrt{5};AB=3\sqrt{13};BC=6\sqrt{13}</math>; now we can apply Heron's formula here, which is <math>\sqrt\frac{(9\sqrt{5}+9\sqrt{13})(9\sqrt{13}-9\sqrt{5})(9\sqrt{5}+3\sqrt{13})(9\sqrt{5}-3\sqrt{13})}{16}=108</math>
 
−
Our answer is <math>\boxed{108}</math>
 
−
~bluesoul
 
  
 
== See also ==
 
== See also ==

Latest revision as of 22:46, 30 June 2024

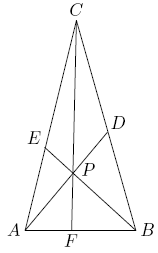
Problem

Point $P$ is inside $\triangle ABC$. Line segments $APD$, $BPE$, and $CPF$ are drawn with $D$ on $BC$, $E$ on $AC$, and $F$ on $AB$ (see the figure below). Given that $AP=6$, $BP=9$, $PD=6$, $PE=3$, and $CF=20$, find the area of $\triangle ABC$.

AIME 1989 Problem 15.png

Solutions

Solution 1 (Ceva's Theorem, Stewart's Theorem)

Let $[RST]$ be the area of polygon $RST$. We'll make use of the following fact: if $P$ is a point in the interior of triangle $XYZ$, and line $XP$ intersects line $YZ$ at point $L$, then $\dfrac{XP}{PL} = \frac{[XPY] + [ZPX]}{[YPZ]}.$

[asy] size(170); pair X = (1,2), Y = (0,0), Z = (3,0); real x = 0.4, y = 0.2, z = 1-x-y; pair P = x*X + y*Y + z*Z; pair L = y/(y+z)*Y + z/(y+z)*Z; draw(X--Y--Z--cycle); draw(X--P); draw(P--L, dotted); draw(Y--P--Z); label("$X$", X, N); label("$Y$", Y, S); label("$Z$", Z, S); label("$P$", P, NE); label("$L$", L, S);[/asy]

This is true because triangles $XPY$ and $YPL$ have their areas in ratio $XP:PL$ (as they share a common height from $Y$), and the same is true of triangles $ZPY$ and $LPZ$.

We'll also use the related fact that $\dfrac{[XPY]}{[ZPX]} = \dfrac{YL}{LZ}$. This is slightly more well known, as it is used in the standard proof of Ceva's theorem.

Now we'll apply these results to the problem at hand.

[asy] size(170); pair C = (1, 3), A = (0,0), B = (1.7,0); real a = 0.5, b= 0.25, c = 0.25; pair P = a*A + b*B + c*C; pair D = b/(b+c)*B + c/(b+c)*C; pair EE = c/(c+a)*C + a/(c+a)*A; pair F = a/(a+b)*A + b/(a+b)*B; draw(A--B--C--cycle); draw(A--P); draw(B--P--C); draw(P--D, dotted); draw(EE--P--F, dotted); label("$A$", A, S); label("$B$", B, S); label("$C$", C, N); label("$D$", D, NE); label("$E$", EE, NW); label("$F$", F, S); label("$P$", P, E); [/asy]

Since $AP = PD = 6$, this means that $[APB] + [APC] = [BPC]$; thus $\triangle BPC$ has half the area of $\triangle ABC$. And since $PE = 3 = \dfrac{1}{3}BP$, we can conclude that $\triangle APC$ has one third of the combined areas of triangle $BPC$ and $APB$, and thus $\dfrac{1}{4}$ of the area of $\triangle ABC$. This means that $\triangle APB$ is left with $\dfrac{1}{4}$ of the area of triangle $ABC$: \[[BPC]: [APC]: [APB] = 2:1:1.\] Since $[APC] = [APB]$, and since $\dfrac{[APC]}{[APB]} = \dfrac{CD}{DB}$, this means that $D$ is the midpoint of $BC$.

Furthermore, we know that $\dfrac{CP}{PF} = \dfrac{[APC] + [BPC]}{[APB]} = 3$, so $CP = \dfrac{3}{4} \cdot CF = 15$.

We now apply Stewart's theorem to segment $PD$ in $\triangle BPC$—or rather, the simplified version for a median. This tells us that \[2 BD^2 + 2 PD^2 = BP^2+ CP^2.\] Plugging in we know, we learn that \begin{align*} 2 BD^2 + 2 \cdot 36 &= 81 + 225 = 306, \\ BD^2 &= 117. \end{align*} Happily, $BP^2 + PD^2 = 81 + 36$ is also equal to 117. Therefore $\triangle BPD$ is a right triangle with a right angle at $B$; its area is thus $\dfrac{1}{2} \cdot 9 \cdot 6 = 27$. As $PD$ is a median of $\triangle BPC$, the area of $BPC$ is twice this, or 54. And we already know that $\triangle BPC$ has half the area of $\triangle ABC$, which must therefore be $\boxed{108}$.

Solution 2 (Mass Points, Stewart's Theorem, Heron's Formula)

Because we're given three concurrent cevians and their lengths, it seems very tempting to apply Mass points. We immediately see that $w_E = 3$, $w_B = 1$, and $w_A = w_D = 2$. Now, we recall that the masses on the three sides of the triangle must be balanced out, so $w_C = 1$ and $w_F = 3$. Thus, $CP = 15$ and $PF = 5$.

Recalling that $w_C = w_B = 1$, we see that $DC = DB$ and $DP$ is a median to $BC$ in $\triangle BCP$. Applying Stewart's Theorem, we have the following: \[\frac{BC}{2}(9^2+15^2)=BC(6^2+ \left(\frac{BC}{2} \right)^2).\] Eliminating $BC$ on both sides, we have: \[\frac 12(9^2+15^2)=6^2+ \left(\frac{BC}{2} \right)^2.\] Combining terms and simplifying numbers, we have: \[153=36+\left(\frac{BC}{2} \right)^2.\] Subtracting 36 to the other side yields: \[117= \left(\frac{BC}{2} \right)^2.\] Finishing it off from there, we find that $BC=2 \sqrt{117}.$ Now, notice that $2[BCP] = [ABC]$, because both triangles share the same base, $BC$ and $h_{\triangle ABC} = 2h_{\triangle BCP}$. Applying Heron's formula on triangle $BCP$ with sides $15$, $9$, and $2\sqrt{117}$, we have: \[\sqrt{(\sqrt{117}+12)(\sqrt{117}+12-9)(\sqrt{117}+12-15)(\sqrt{117}+12-2\sqrt{117})}.\] Combining terms results in: \[\sqrt{(\sqrt{117}+12)(\sqrt{117}+3)(\sqrt{117}-3)(-\sqrt{117}+12)}.\] Notice that these factors can be grouped into a difference of squares: \[\sqrt{(144-\sqrt{117}^2)(\sqrt{117}^2-9)}.\] Since $\sqrt{117}^2=117$, we have: \[\sqrt{(27)(108)}.\] After simplifying this radical, we find that it equals $54.$ Therefore, $[BCP] = 54$, and hence $[ABC]=2 \cdot 54= \boxed{108}$.

(The original author made a mistake in their solution. Corrected and further explained by dbnl.)

Solution 3 (Ceva's Theorem, Stewart's Theorem)

Using a different form of Ceva's Theorem, we have $\frac {y}{x + y} + \frac {6}{6 + 6} + \frac {3}{3 + 9} = 1\Longleftrightarrow\frac {y}{x + y} = \frac {1}{4}$

Solving $4y = x + y$ and $x + y = 20$, we obtain $x = CP = 15$ and $y = FP = 5$.

Let $Q$ be the point on $AB$ such that $FC \parallel QD$. Since $AP = PD$ and $FP\parallel QD$, $QD = 2FP = 10$. (Stewart's Theorem)

Also, since $FC\parallel QD$ and $QD = \frac{FC}{2}$, we see that $FQ = QB$, $BD = DC$, etc. (Stewart's Theorem) Similarly, we have $PR = RB$ ($= \frac12PB = 7.5$) and thus $RD = \frac12PC = 4.5$.

$PDR$ is a $3-4-5$ right triangle, so $\angle PDR$ ($\angle ADQ$) is $90^\circ$. Therefore, the area of $\triangle ADQ = \frac12\cdot 12\cdot 6 = 36$. Using area ratio, $\triangle ABC = \triangle ADB\times 2 = \left(\triangle ADQ\times \frac32\right)\times 2 = 36\cdot 3 = \boxed{108}$.

Solution 4 (Stewart's Theorem)

First, let $[AEP]=a, [AFP]=b,$ and $[ECP]=c.$ Thus, we can easily find that $\frac{[AEP]}{[BPD]}=\frac{3}{9}=\frac{1}{3} \Leftrightarrow [BPD]=3[AEP]=3a.$ Now, $\frac{[ABP]}{[BPD]}=\frac{6}{6}=1\Leftrightarrow [ABP]=3a.$ In the same manner, we find that $[CPD]=a+c.$ Now, we can find that $\frac{[BPC]}{[PEC]}=\frac{9}{3}=3 \Leftrightarrow \frac{(3a)+(a+c)}{c}=3 \Leftrightarrow c=2a.$ We can now use this to find that $\frac{[APC]}{[AFP]}=\frac{[BPC]}{[BFP]}=\frac{PC}{FP} \Leftrightarrow \frac{3a}{b}=\frac{6a}{3a-b} \Leftrightarrow a=b.$ Plugging this value in, we find that $\frac{FC}{FP}=3 \Leftrightarrow PC=15, FP=5.$ Now, since $\frac{[AEP]}{[PEC]}=\frac{a}{2a}=\frac{1}{2},$ we can find that $2AE=EC.$ Setting $AC=b,$ we can apply Stewart's Theorem on triangle $APC$ to find that $(15)(15)(\frac{b}{3})+(6)(6)(\frac{2b}{3})=(\frac{2b}{3})(\frac{b}{3})(b)+(b)(3)(3).$ Solving, we find that $b=\sqrt{405} \Leftrightarrow AE=\frac{b}{3}=\sqrt{45}.$ But, $3^2+6^2=45,$ meaning that $\angle{APE}=90 \Leftrightarrow [APE]=\frac{(6)(3)}{2}=9=a.$ Since $[ABC]=a+a+2a+2a+3a+3a=12a=(12)(9)=108,$ we conclude that the answer is $\boxed{108}$.

Solution 5 (Mass of a Point, Stewart's Theorem, Heron's Formula)

Firstly, since they all meet at one single point, denoting the mass of them separately. Assuming $M(A)=6;M(D)=6;M(B)=3;M(E)=9$; we can get that $M(P)=12;M(F)=9;M(C)=3$; which leads to the ratio between segments, \[\frac{CE}{AE}=2;\frac{BF}{AF}=2;\frac{BD}{CD}=1.\] Denoting that $CE=2x;AE=x; AF=y; BF=2y; CD=z; DB=z.$

Now we know three cevians' length, Applying Stewart theorem to them, getting three different equations: \begin{align} (3x)^2 \cdot 2y+(2z)^2 \cdot y&=(3y)(2y^2+400), \\ (3y)^2 \cdot z+(3x)^2 \cdot z&=(2z)(z^2+144), \\ (2z)^2 \cdot x+(3y)^2 \cdot x&=(3x)(2x^2+144). \end{align} After solving the system of equation, we get that $x=3\sqrt{5};y=\sqrt{13};z=3\sqrt{13}$;

pulling $x,y,z$ back to get the length of $AC=9\sqrt{5};AB=3\sqrt{13};BC=6\sqrt{13}$; now we can apply Heron's formula here, which is \[\sqrt\frac{(9\sqrt{5}+9\sqrt{13})(9\sqrt{13}-9\sqrt{5})(9\sqrt{5}+3\sqrt{13})(9\sqrt{5}-3\sqrt{13})}{16}=108.\]

Our answer is $\boxed{108}$.

~bluesoul

Note (how to find x and y without the system of equations)

To ease computation, we can apply Stewart's Theorem to find $x$, $y$, and $z$ directly. Since $M(C)=3$ and $M(F)=9$, $\overline{PC}=15$ and $\overline{PF}=5$. We can apply Stewart's Theorem on $\triangle CPE$ to get $(2x+x)(2x \cdot x) + 3^2 \cdot 3x = 15^2 \cdot x + 6^2\cdot 2x$. Solving, we find that $x=3\sqrt{5}$. We can do the same on $\triangle APB$ and $\triangle BPC$ to obtain $y$ and $z$. We proceed with Heron's Formula as the solution states.

~kn07

Solution 6 (easier version of Solution 5)

In Solution 5, instead of finding all of $x, y, z$, we only need $y, z$. This is because after we solve for $y, z$, we can notice that $\triangle BAD$ is isosceles with $AB = BD$. Because $P$ is the midpoint of the base, $BP$ is an altitude of $\triangle BAD$. Therefore, $[BAD] = \frac{(AD)(BP)}{2} = \frac{12 \cdot 9}{2} = 54$. Using the same altitude property, we can find that $[ABC] = 2[BAD] = 2 \cdot 54 = \boxed{108}$.

-NL008

Solution 7 (Mass Points, Stewart's Theorem, Simple Version)

Set $AF=x,$ and use mass points to find that $PF=5$ and $BF=2x.$ Using Stewart's Theorem on $APB,$ we find that $AB=3\sqrt{13}.$ Then we notice that $APB$ is right, which means the area of $APB$ is $27.$ Because $CF=4\cdot PF,$ the area of $ABC$ is $4$ times the area of $APB,$ which means the area of $ABC=4\cdot 27=\boxed{108}.$

Solution 8 (Ratios, Auxiliary Lines and 3-4-5 triangle)

We try to solve this using only elementary concepts. Let the areas of triangles $BCP$, $ACP$ and $ABP$ be $X$, $Y$ and $Z$ respectively. Then $\frac{X}{Y+Z}=\frac{6}{6}=1$ and $\frac{Y}{X+Z}=\frac{3}{9}=\frac{1}{3}$. Hence $\frac{X}{2}=Y=Z$. Similarly $\frac{FP}{PC}=\frac{Z}{X+Y}=\frac{1}{3}$ and since $CF=20$ we then have $FP=5$. Additionally we now see that triangles $FPE$ and $CPB$ are similar, so $FE \parallel BC$ and $\frac{FE}{BC} = \frac{1}{3}$. Hence $\frac{AF}{FB}=\frac{1}{2}$. Now construct a point $K$ on segment $BP$ such that $BK=6$ and $KP=3$, we will have $FK \parallel AP$, and hence $\frac{FK}{AP} = \frac{FK}{6} = \frac{2}{3}$, giving $FK=4$. Triangle $FKP$ is therefore a 3-4-5 triangle! So $FK \perp BE$ and so $AP \perp BE$. Then it is easy to calculate that $Z = \frac{1}{2} \times 6 \times 9 = 27$ and the area of triangle $ABC = X+Y+Z = 4Z = 4 \times 27 = \boxed{108}$. ~Leole


Solution 9 (Just Trig Bash)

We start with mass points as in Solution 2, and receive $BF:AF = 2$, $BD:CD = 1$, $CE:AE = 2$. Law of Cosines on triangles $ADB$ and $ADC$ with $\theta = \angle ADB$ and $BD=DC=x$ gives \[36+x^2-12x\cos \theta = 81\] \[36+x^2-12x\cos (180-\theta) = 36+x^2+12x\cos \theta = 225\] Adding them: $72+2x^2=306 \implies x=3\sqrt{13}$, so $BC = 6\sqrt{13}$. Similarly, $AB = 3\sqrt{13}$ and $AC = 9\sqrt{5}$. Using Heron's, \[[ \triangle ABC ]= \sqrt{\left(\dfrac{9\sqrt{13}+9\sqrt{5}}{2}\right)\left(\dfrac{9\sqrt{13}09\sqrt{5}}{2}\right)\left(\dfrac{3\sqrt{13}+9\sqrt{5}}{2}\right)\left(\dfrac{-3\sqrt{13}+9\sqrt{5}}{2}\right)} = \boxed{108}.\]

~sml1809

See also

1989 AIME (Problems • Answer Key • Resources)
Preceded by
Problem 14 		Followed by
Final Question
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1989_AIME_Problems/Problem_15&oldid=221375"