Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1998 AIME Problems/Problem 10"

(fmt, failed to parse!!)
 
(3 intermediate revisions by 3 users not shown)
Line 1: Line 1:
 
== Problem ==
 
== Problem ==
−
Eight [[sphere]]s of [[radius]] 100 are placed on a flat [[plane|surface]] so that each sphere is [[tangent]] to two others and their [[center]]s are the vertices of a regular [[octagon]].  A ninth sphere is placed on the flat surface so that it is tangent to each of the other eight spheres.  The radius of this last sphere is <math>\displaystyle a + \displaystyle b\sqrt {c} \displaystyle,</math> where <math>a, b,</math> and <math>c</math> are [[positive]] [[integer]]s, and <math>c</math> is not divisible by the square of any [[prime]].  Find <math>\displaystyle a + b + c</math>.
+
Eight [[sphere]]s of [[radius]] 100 are placed on a flat [[plane|surface]] so that each sphere is [[tangent]] to two others and their [[center]]s are the vertices of a regular [[octagon]].  A ninth sphere is placed on the flat surface so that it is tangent to each of the other eight spheres.  The radius of this last sphere is <math>a +b\sqrt {c},</math> where <math>a, b,</math> and <math>c</math> are [[positive]] [[integer]]s, and <math>c</math> is not divisible by the square of any [[prime]].  Find <math>a + b + c</math>.
  
 
__TOC__
 
__TOC__
Line 15: Line 15:
 
If we draw the segment containing the centers and the radii [[perpendicular]] to the flat surface, we get a [[trapezoid]]; if we draw the segment parallel to the surface that connects the center of the smaller sphere to the radii of the larger, we get a right triangle. Call that segment <math>x</math>. Then by the [[Pythagorean Theorem]]:
 
If we draw the segment containing the centers and the radii [[perpendicular]] to the flat surface, we get a [[trapezoid]]; if we draw the segment parallel to the surface that connects the center of the smaller sphere to the radii of the larger, we get a right triangle. Call that segment <math>x</math>. Then by the [[Pythagorean Theorem]]:
  
−
:<math>x^2 + (r-100)^2 = (r+100)^2</math>
+
<cmath>x^2 + (r-100)^2 = (r+100)^2 \Longrightarrow x = 20\sqrt{r}</cmath>
−
:<math>x^2 = 400r</math>
 
−
:<math>x = 20\sqrt{r}</math>
 
  
−
Now let us examine the top view again:
+
[[Image:1998_AIME-10c.png|450px]]
  
−
[[Image:1998_AIME-10c.png|450px]]
+
<math>x</math> is the distance from one of the vertices of the octagon to the center, so the diagonal of the octagon is of length <math>2x =40\sqrt{r}</math>. We can draw another [[right triangle]] as shown above. One leg has a length of <math>200</math>. The other can be found by partitioning the leg into three sections and using <math>45-45-90 \triangle</math>s to see that the leg is <math>100\sqrt{2} + 200 + 100\sqrt{2} = 200(\sqrt{2} + 1)</math>. Pythagorean Theorem:
 +
 
 +
<cmath>\begin{eqnarray*}
 +
(40\sqrt{r})^2 &=& 200^2 + [200(\sqrt{2}+1)]^2\\
 +
1600r &=& 200^2[(1 + \sqrt{2})^2 + 1] \\
 +
r &=& 100 + 50\sqrt{2}
 +
\end{eqnarray*}</cmath>
 +
 
 +
Thus <math>a + b + c = 100 + 50 + 2 = \boxed{152}</math>.
 +
 
 +
==Solution 2==
 +
Isolate a triangle, with base length <math>200</math> (a side of the octagon). This triangle is obviously isoceles. Denote the other side length as <math>x</math>. Since the interior angle is <math>45</math> degrees (due to the shape being an octagon), then we can apply Law of Cosines to this triangle. We get:
 +
<cmath>\begin{eqnarray*}
 +
200^2 &=& 2x^2 - 2x^2*cos(45^\circ) \\ &=& 2x^2 - 2x^2*\frac{\sqrt{2}}{2} \\ &=& (2-\sqrt{2})x^2
 +
\end{eqnarray*}</cmath>
 +
 
 +
And thus <cmath>x = \frac{200}{\sqrt{2-\sqrt{2}}}</cmath>
 +
 
 +
From the above, <math>x = 20\sqrt{r}</math>, so we get
 +
 
 +
<cmath>\begin{eqnarray*}
 +
r &=& (\frac{200}{20(\sqrt{2-\sqrt{2}})})^2 \\ &=& (\frac{10}{\sqrt{2-\sqrt{2}})})^2 \cdot \frac{2+\sqrt{2}}{2+\sqrt{2}} \\ &=& \frac{200 + 100\sqrt{2}}{2} \\ &=& 100 + 50\sqrt{2}
 +
\end{eqnarray*}</cmath>
 +
 
 +
And hence the answer is <math>100 + 50 + 2 \Rightarrow \boxed{152}</math>
  
−
<math>x</math> is the distance from one of the vertices of the octagon to the center, so the diagonal of the octagon is of length <math>\displaystyle 2x = \displaystyle 40\sqrt{r} \displaystyle</math>. We can draw another [[right triangle]] as shown above. One leg has a length of <math>200</math>. The other can be found by partitioning the leg into three sections and using <math>45-45-90 \triangle</math>s  to see that the leg is <math>100\sqrt{2} + 200 + 100\sqrt{2} = 200(\sqrt{2} + 1)</math>. Pythagorean Theorem:
 
  
−
<div style="text-align:center;"><math>200^2 + [200(\sqrt{2}+1)]^2 = (40\sqrt{r})^2</math><br />
 
−
<math>200^2[(1 + \sqrt{2})^2 + 1] = 1600r</math><br />
 
−
<math>\displaystyle 25(4 + 2\sqrt{2}) = r</math><br />
 
−
<math>r = 100 + 50\sqrt{2}</math></div>
 
  
−
Thus <math>a + b + c = 100 + 50 + 2 = 152</math>.
 
  
 
== See also ==
 
== See also ==
Line 36: Line 52:
  
 
[[Category:Intermediate Geometry Problems]]
 
[[Category:Intermediate Geometry Problems]]
 +
{{MAA Notice}}

Latest revision as of 12:02, 5 August 2019

Problem

Eight spheres of radius 100 are placed on a flat surface so that each sphere is tangent to two others and their centers are the vertices of a regular octagon. A ninth sphere is placed on the flat surface so that it is tangent to each of the other eight spheres. The radius of this last sphere is $a +b\sqrt {c},$ where $a, b,$ and $c$ are positive integers, and $c$ is not divisible by the square of any prime. Find $a + b + c$.

Solution

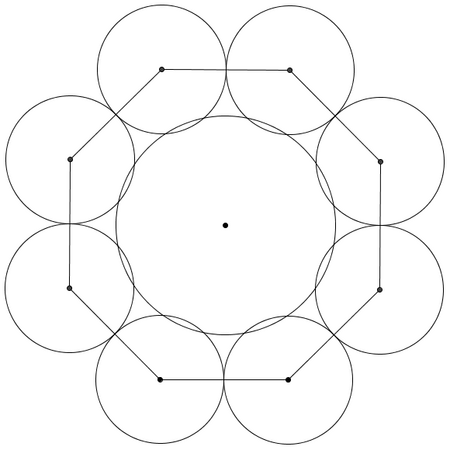
The key is to realize the significance that the figures are spheres, not circles. The 2D analogue of the diagram onto the flat surface will not contain 8 circles tangent to a ninth one; instead the circles will overlap since the middle sphere has a larger radius and will sort of “bulge” out.

1998 AIME-10a.png

Let us examine the relation between one of the outside 8 spheres and the center one (with radius $r$):

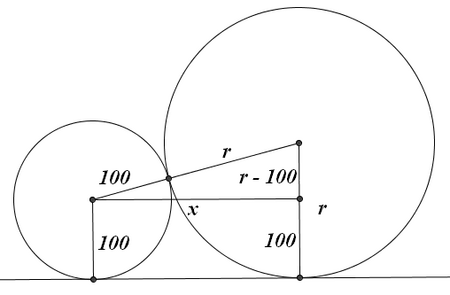
1998 AIME-10b.png

If we draw the segment containing the centers and the radii perpendicular to the flat surface, we get a trapezoid; if we draw the segment parallel to the surface that connects the center of the smaller sphere to the radii of the larger, we get a right triangle. Call that segment $x$. Then by the Pythagorean Theorem:

\[x^2 + (r-100)^2 = (r+100)^2 \Longrightarrow x = 20\sqrt{r}\]

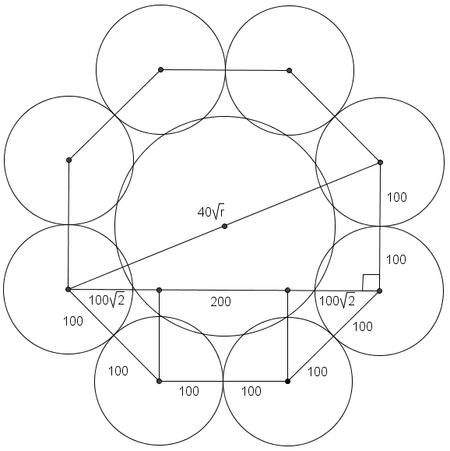
1998 AIME-10c.png

$x$ is the distance from one of the vertices of the octagon to the center, so the diagonal of the octagon is of length $2x =40\sqrt{r}$. We can draw another right triangle as shown above. One leg has a length of $200$. The other can be found by partitioning the leg into three sections and using $45-45-90 \triangle$s to see that the leg is $100\sqrt{2} + 200 + 100\sqrt{2} = 200(\sqrt{2} + 1)$. Pythagorean Theorem:

\begin{eqnarray*} (40\sqrt{r})^2 &=& 200^2 + [200(\sqrt{2}+1)]^2\\ 1600r &=& 200^2[(1 + \sqrt{2})^2 + 1] \\ r &=& 100 + 50\sqrt{2} \end{eqnarray*}

Thus $a + b + c = 100 + 50 + 2 = \boxed{152}$.

Solution 2

Isolate a triangle, with base length $200$ (a side of the octagon). This triangle is obviously isoceles. Denote the other side length as $x$. Since the interior angle is $45$ degrees (due to the shape being an octagon), then we can apply Law of Cosines to this triangle. We get: \begin{eqnarray*} 200^2 &=& 2x^2 - 2x^2*cos(45^\circ) \\ &=& 2x^2 - 2x^2*\frac{\sqrt{2}}{2} \\ &=& (2-\sqrt{2})x^2 \end{eqnarray*}

And thus \[x = \frac{200}{\sqrt{2-\sqrt{2}}}\]

From the above, $x = 20\sqrt{r}$, so we get

\begin{eqnarray*} r &=& (\frac{200}{20(\sqrt{2-\sqrt{2}})})^2 \\ &=& (\frac{10}{\sqrt{2-\sqrt{2}})})^2 \cdot \frac{2+\sqrt{2}}{2+\sqrt{2}} \\ &=& \frac{200 + 100\sqrt{2}}{2} \\ &=& 100 + 50\sqrt{2} \end{eqnarray*}

And hence the answer is $100 + 50 + 2 \Rightarrow \boxed{152}$



See also

1998 AIME (Problems • Answer Key • Resources)
Preceded by
Problem 9 		Followed by
Problem 11
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1998_AIME_Problems/Problem_10&oldid=108228"