Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1998 AIME Problems/Problem 6"

(prob / sol)
 
(2 intermediate revisions by 2 users not shown)
Line 1: Line 1:
 
== Problem ==
 
== Problem ==
−
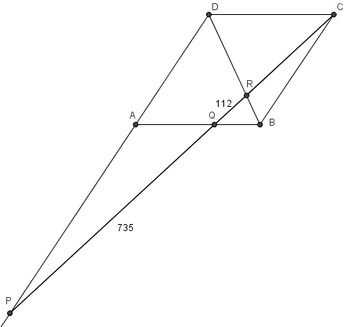
Let <math>A\displaystyle BCD</math> be a [[parallelogram]].  Extend <math>\overline{DA}</math> through <math>A</math> to a point <math>P,</math> and let <math>\overline{PC}</math> meet <math>\overline{AB}</math> at <math>Q</math> and <math>\overline{DB}</math> at <math>R.</math>  Given that <math>PQ = 735</math> and <math>QR = 112,</math> find <math>RC.</math>
+
Let <math>ABCD</math> be a [[parallelogram]].  Extend <math>\overline{DA}</math> through <math>A</math> to a point <math>P,</math> and let <math>\overline{PC}</math> meet <math>\overline{AB}</math> at <math>Q</math> and <math>\overline{DB}</math> at <math>R.</math>  Given that <math>PQ = 735</math> and <math>QR = 112,</math> find <math>RC.</math>
  
 
== Solution ==
 
== Solution ==
−
[[Image:AIME_1998-6.png|500px]]
+
=== Solution 1 ===
 +
[[Image:AIME_1998-6.png|350px]]
  
−
There are several [[similar triangles]]. <math>\triangle PAQ \displaystyle \sim \triangle PDC</math>, so we can write the [[proportion]]:
+
There are several [[similar triangles]]. <math>\triangle PAQ\sim \triangle PDC</math>, so we can write the [[proportion]]:
  
 
<div style="text-align:center;">
 
<div style="text-align:center;">
Line 11: Line 12:
 
</div>  
 
</div>  
  
−
Also, <math>\triangle BRQ \displaystyle \sim DRC</math>, so:
+
Also, <math>\triangle BRQ\sim DRC</math>, so:
  
 
<div style="text-align:center;">
 
<div style="text-align:center;">
−
<math>\displaystyle \frac{QR}{RC} = \frac{QB}{CD} = \frac{112}{RC} = \frac{CD - AQ}{CD} = 1 - \frac{AQ}{CD} \displaystyle</math><br />
+
<math>\frac{QR}{RC} = \frac{QB}{CD} = \frac{112}{RC} = \frac{CD - AQ}{CD} = 1 - \frac{AQ}{CD}</math><br />
  
 
<math>\frac{AQ}{CD} = 1 - \frac{112}{RC} = \frac{RC - 112}{RC}</math>
 
<math>\frac{AQ}{CD} = 1 - \frac{112}{RC} = \frac{RC - 112}{RC}</math>
Line 24: Line 25:
 
<math>\frac{AQ}{CD} = \frac{735}{847 + RC} = \frac{RC - 112}{RC}</math><br />
 
<math>\frac{AQ}{CD} = \frac{735}{847 + RC} = \frac{RC - 112}{RC}</math><br />
  
−
<math>\displaystyle735RC = (RC + 847)(RC - 112)</math><br />
+
<math>735RC = (RC + 847)(RC - 112)</math><br />
 
<math>0 = RC^2 - 112\cdot847</math>
 
<math>0 = RC^2 - 112\cdot847</math>
 
</div>
 
</div>
  
−
Thus, <math> RC = \sqrt{112*847} = 308 \displaystyle</math>.  
+
Thus, <math> RC = \sqrt{112*847} = 308</math>.
 +
 
 +
=== Solution 2 ===
 +
 
 +
We have <math>\triangle BRQ\sim \triangle DRC</math> so <math>\frac{112}{RC} = \frac{BR}{DR}</math>. We also have <math>\triangle BRC \sim \triangle DRP</math> so <math>\frac{ RC}{847} = \frac {BR}{DR}</math>. Equating the two results gives <math>\frac{112}{RC} =  \frac{ RC}{847}</math> and so <math>RC^2=112*847</math> which solves to <math>RC=\boxed{308}</math>
  
 
== See also ==
 
== See also ==
Line 34: Line 39:
  
 
[[Category:Intermediate Geometry Problems]]
 
[[Category:Intermediate Geometry Problems]]
 +
{{MAA Notice}}

Latest revision as of 18:38, 4 July 2013

Problem

Let $ABCD$ be a parallelogram. Extend $\overline{DA}$ through $A$ to a point $P,$ and let $\overline{PC}$ meet $\overline{AB}$ at $Q$ and $\overline{DB}$ at $R.$ Given that $PQ = 735$ and $QR = 112,$ find $RC.$

Solution

Solution 1

AIME 1998-6.png

There are several similar triangles. $\triangle PAQ\sim \triangle PDC$, so we can write the proportion:

$\frac{AQ}{CD} = \frac{PQ}{PC} = \frac{735}{112 + 735 + RC} = \frac{735}{847 + RC}$

Also, $\triangle BRQ\sim DRC$, so:

$\frac{QR}{RC} = \frac{QB}{CD} = \frac{112}{RC} = \frac{CD - AQ}{CD} = 1 - \frac{AQ}{CD}$

$\frac{AQ}{CD} = 1 - \frac{112}{RC} = \frac{RC - 112}{RC}$

Substituting,

$\frac{AQ}{CD} = \frac{735}{847 + RC} = \frac{RC - 112}{RC}$

$735RC = (RC + 847)(RC - 112)$
$0 = RC^2 - 112\cdot847$

Thus, $RC = \sqrt{112*847} = 308$.

Solution 2

We have $\triangle BRQ\sim \triangle DRC$ so $\frac{112}{RC} = \frac{BR}{DR}$. We also have $\triangle BRC \sim \triangle DRP$ so $\frac{ RC}{847} = \frac {BR}{DR}$. Equating the two results gives $\frac{112}{RC} = \frac{ RC}{847}$ and so $RC^2=112*847$ which solves to $RC=\boxed{308}$

See also

1998 AIME (Problems • Answer Key • Resources)
Preceded by
Problem 5 		Followed by
Problem 7
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1998_AIME_Problems/Problem_6&oldid=55079"