Difference between revisions of "2002 AMC 12B Problems/Problem 14"
(Tag: Undo) |
(Tag: Undo) |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{duplicate|[[2002 AMC 12B Problems|2002 AMC 12B #14]] and [[2002 AMC 10B Problems|2002 AMC 10B #18]]}} | {{duplicate|[[2002 AMC 12B Problems|2002 AMC 12B #14]] and [[2002 AMC 10B Problems|2002 AMC 10B #18]]}} | ||
== Problem == | == Problem == | ||
| + | <!-- don't remove the following tag, for PoTW on the Wiki front page--><onlyinclude>Four distinct [[circle]]s are drawn in a [[plane]]. What is the maximum number of points where at least two of the circles intersect?<!-- don't remove the following tag, for PoTW on the Wiki front page--></onlyinclude> | ||
| − | + | <math>\mathrm{(A)}\ 8 | |
| + | \qquad\mathrm{(B)}\ 9 | ||
| + | \qquad\mathrm{(C)}\ 10 | ||
| + | \qquad\mathrm{(D)}\ 12 | ||
| + | \qquad\mathrm{(E)}\ 16</math> | ||
| − | ==Solution 2== | + | == Solution 1== |
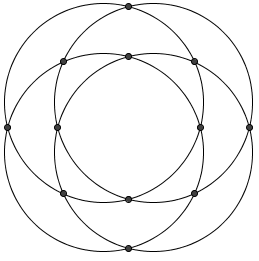
| + | For any given pair of circles, they can intersect at most <math>2</math> times. Since there are <math>{4\choose 2} = 6</math> pairs of circles, the maximum number of possible intersections is <math>6 \cdot 2 = 12</math>. We can construct such a situation as below, so the answer is <math>\boxed{\mathrm{(D)}\ 12}</math>. | ||
| − | ==Solution 3== | + | [[Image:2002_12B_AMC-14.png]] |
| + | |||
| + | ==Solution 2== | ||
| + | Because a pair or circles can intersect at most <math>2</math> times, the first circle can intersect the second at <math>2</math> points, the third can intersect the first two at <math>4</math> points, and the fourth can intersect the first three at <math>6</math> points. This means that our answer is <math>2+4+6=\boxed{\mathrm{(D)}\ 12}.</math> | ||
| + | |||
| + | ==Solution 3== | ||
| + | |||
| + | Pick a circle any circle- <math>4</math> ways. Then, pick any other circle- <math>3</math> ways. For each of these circles, there will be <math>2</math> intersections for a total of <math>4*3*2</math> = <math>24</math> intersections. However, we have counted each intersection twice, so we divide for overcounting. Therefore, we reach a total of <math>\frac{24}{2}=\boxed{12}</math>, which corresponds to <math>\text{(D)}</math>. | ||
| + | |||
| + | == See also == | ||
| + | {{AMC10 box|year=2002|ab=B|num-b=17|num-a=19}} | ||
| + | {{AMC12 box|year=2002|ab=B|num-b=13|num-a=15}} | ||
| + | |||
| + | [[Category:Introductory Combinatorics Problems]] | ||
| + | {{MAA Notice}} | ||
Latest revision as of 13:04, 12 July 2021
- The following problem is from both the 2002 AMC 12B #14 and 2002 AMC 10B #18, so both problems redirect to this page.
Problem
Four distinct circles are drawn in a plane. What is the maximum number of points where at least two of the circles intersect?
Solution 1
For any given pair of circles, they can intersect at most 
times. Since there are 
pairs of circles, the maximum number of possible intersections is 
. We can construct such a situation as below, so the answer is 
.
Solution 2
Because a pair or circles can intersect at most times, the first circle can intersect the second at points, the third can intersect the first two at 
points, and the fourth can intersect the first three at 
points. This means that our answer is 
Solution 3
Pick a circle any circle- ways. Then, pick any other circle- 
ways. For each of these circles, there will be intersections for a total of 
= 
intersections. However, we have counted each intersection twice, so we divide for overcounting. Therefore, we reach a total of 
, which corresponds to 
.
See also
| 2002 AMC 10B (Problems • Answer Key • Resources) | ||
| Preceded by Problem 17 |
Followed by Problem 19 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
| 2002 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 13 |
Followed by Problem 15 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 
