Difference between revisions of "2021 JMPSC Sprint Problems/Problem 4"
(→Problem) |
(→Solution) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 9: | Line 9: | ||
==Solution== | ==Solution== | ||
| − | + | Simply look at the board. | |
| + | |||
| + | Draw the paths in which they can go. | ||
| + | |||
| + | You will see that they will intersect at these squares: | ||
| + | D4 | ||
| + | B4 | ||
| + | E7 | ||
| + | E3 | ||
| + | |||
| + | Therefore, four squares can be attacked by both the bishop and the rook if they each take one move. | ||
| + | -OofPirate | ||
| + | |||
| + | |||
| + | |||
| + | ==See also== | ||
| + | #[[2021 JMPSC Sprint Problems|Other 2021 JMPSC Sprint Problems]] | ||
| + | #[[2021 JMPSC Sprint Answer Key|2021 JMPSC Sprint Answer Key]] | ||
| + | #[[JMPSC Problems and Solutions|All JMPSC Problems and Solutions]] | ||
| + | {{JMPSC Notice}} | ||
Latest revision as of 16:12, 11 July 2021
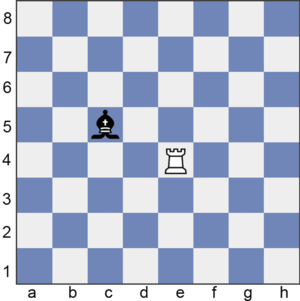
Problem
A standard chess-board is an 8 by 8 grid of squares. A bishop is placed at square C5 (row 5, column C) and a rook is placed at square E4 (row 4, column E). How many squares can be attacked by both the bishop and rook if they each take one move?
(The bishop can attack any square in the same diagonal as itself, including squares A7, F8, G1, D6, and so on. The rook can attack any square in the same row or column as itself, including squares E5, E8, E4, C4, and so on.)
Solution
Simply look at the board.
Draw the paths in which they can go.
You will see that they will intersect at these squares: D4 B4 E7 E3
Therefore, four squares can be attacked by both the bishop and the rook if they each take one move. -OofPirate
See also
The problems on this page are copyrighted by the Junior Mathematicians' Problem Solving Competition.