Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2021 JMPSC Sprint Problems/Problem 3"

(→‎Problem)
 
(4 intermediate revisions by 3 users not shown)
Line 6: Line 6:
  
 
==Solution==
 
==Solution==
−
asdf
+
 
 +
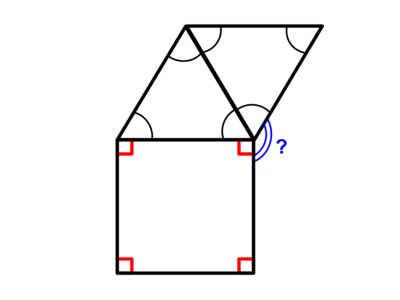
It is given that the right angles are <math>90</math> degrees, and that all the angles in the two triangles are all equal. We can already infer that the black angles are all <math>60</math> degrees, since they are equilateral triangles.
 +
 
 +
There are <math>360</math> degrees in a whole circle. We are given two of the black curves, and a <math>90</math> degree angle, in which all three of them add up to <math>210</math> degrees.
 +
 
 +
<math>360-210=150</math>. Therefore, the angle marked with a question mark has a measure of <math>150</math> degrees.
 +
 
 +
-OofPirate
 +
 
 +
== Solution 2 ==
 +
<math>360^{\circ}-90^{\circ}-60^{\circ}-60^{\circ}=\boxed{150^{\circ}}</math>
 +
 
 +
- kante314 -
 +
 
 +
==See also==
 +
#[[2021 JMPSC Sprint Problems|Other 2021 JMPSC Sprint Problems]]
 +
#[[2021 JMPSC Sprint Answer Key|2021 JMPSC Sprint Answer Key]]
 +
#[[JMPSC Problems and Solutions|All JMPSC Problems and Solutions]]
 +
{{JMPSC Notice}}

Latest revision as of 09:41, 12 July 2021

Problem

If all angles marked with a red square are $90^\circ$ and all angles marked with one black curve are equal, find the measure of the angle with a question mark.

Sprint4.png

Solution

It is given that the right angles are $90$ degrees, and that all the angles in the two triangles are all equal. We can already infer that the black angles are all $60$ degrees, since they are equilateral triangles.

There are $360$ degrees in a whole circle. We are given two of the black curves, and a $90$ degree angle, in which all three of them add up to $210$ degrees.

$360-210=150$. Therefore, the angle marked with a question mark has a measure of $150$ degrees.

-OofPirate

Solution 2

$360^{\circ}-90^{\circ}-60^{\circ}-60^{\circ}=\boxed{150^{\circ}}$

- kante314 -

See also

  1. Other 2021 JMPSC Sprint Problems
  2. 2021 JMPSC Sprint Answer Key
  3. All JMPSC Problems and Solutions

The problems on this page are copyrighted by the Junior Mathematicians' Problem Solving Competition. JMPSC.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2021_JMPSC_Sprint_Problems/Problem_3&oldid=158216"