Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2021 AIME II Problems/Problem 12"

m (→‎Solution 1 (Law of Cosines): The solution not only uses the Law of Cosines, but also the Sines formula. So, the revised title is a bit more appropriate.)
(→‎Note 2)
 
(42 intermediate revisions by 8 users not shown)
Line 1: Line 1:
 
==Problem==
 
==Problem==
 
A convex quadrilateral has area <math>30</math> and side lengths <math>5, 6, 9,</math> and <math>7,</math> in that order. Denote by <math>\theta</math> the measure of the acute angle formed by the diagonals of the quadrilateral. Then <math>\tan \theta</math> can be written in the form <math>\tfrac{m}{n}</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m + n</math>.
 
A convex quadrilateral has area <math>30</math> and side lengths <math>5, 6, 9,</math> and <math>7,</math> in that order. Denote by <math>\theta</math> the measure of the acute angle formed by the diagonals of the quadrilateral. Then <math>\tan \theta</math> can be written in the form <math>\tfrac{m}{n}</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m + n</math>.
−
 
−
==Diagram==
 
−
[[File:2021 AIME II Problem 12 Diagram.png|center]]
 
−
 
−
~MRENTHUSIASM (by Geometry Expressions)
 
  
 
==Solution 1 (Sines and Cosines)==
 
==Solution 1 (Sines and Cosines)==
−
===Solution 1.1 (Version 1)===
 
−
We denote by <math>A</math>, <math>B</math>, <math>C</math> and <math>D</math> four vertices of this quadrilateral, such that <math>AB = 5</math>, <math>BC = 6</math>, <math>CD = 9</math>, <math>DA = 7</math>.
 
−
We denote by <math>E</math> the point that two diagonals <math>AC</math> and <math>BD</math> meet at.
 
−
To simplify the notation, we denote <math>a = AE</math>, <math>b = BE</math>, <math>c = CE</math>, <math>d = DE</math>.
 
−
 
−
We denote <math>\theta = \angle AED</math>. Hence, <math>\angle AEB = \angle CED = 180^\circ - \theta</math> and <math>\angle BEC = \theta</math>.
 
−
 
−
First, we use the triangle area formula with sines to write down an equation of the area of the quadrilateral <math>ABCD</math>.
 
−
 
−
We have
 
−
<cmath>\begin{align*}
 
−
{\rm Area} \ ABCD
 
−
& = {\rm Area} \ \triangle ABE + {\rm Area} \ \triangle BCE + {\rm Area} \ \triangle CDE + {\rm Area} \ \triangle DAE \\
 
−
& = \frac{1}{2} ab \sin \angle AEB + \frac{1}{2} bc \sin \angle BEC + \frac{1}{2} cd \sin \angle CED + \frac{1}{2} da \sin \angle DEA \\
 
−
& = \frac{1}{2} ab \sin \theta + \frac{1}{2} bc \sin \left( 180^\circ - \theta \right)
 
−
+ \frac{1}{2} cd \sin \theta + \frac{1}{2} da \sin \left( 180^\circ - \theta \right) \\
 
−
& = \frac{1}{2} ab \sin \theta + \frac{1}{2} bc \sin \theta
 
−
+ \frac{1}{2} cd \sin \theta + \frac{1}{2} da \sin \theta \\
 
−
& = \frac{1}{2} \left( ab + bc + cd + da \right) \sin \theta,
 
−
\end{align*}</cmath>
 
−
where the second equality follows from the formula to use the sine function to compute a triangle area, the the fourth equality follows from the property that <math>\sin \left( 180^\circ - \theta \right) = \sin \theta</math>.
 
−
 
−
Because <math>{\rm Area} \ ABCD = 30</math>, we have <cmath>\left( ab + bc + cd + da \right) \sin \theta = 60 . \ \ \ (1)</cmath>
 
−
Second, we use the law of cosines to establish four equations for four sides of the quadrilateral <math>ABCD</math>.
 
−
 
−
In <math>\triangle AEB</math>, following from the law of cosines, we have <cmath>a^2 + b^2 - 2 a b \cos \angle AEB = AB^2.</cmath>
 
−
Because <math>\cos \angle AEB = \cos \left(180^\circ - \theta \right) = \cos \theta</math> and <math>AB = 5</math>, we have <cmath>a^2 + b^2 + 2 a b \cos \theta = 5^2. \ \ \ (2)</cmath>
 
−
In <math>\triangle BEC</math>, following from the law of cosines, we have <cmath>b^2 + c^2 - 2 b c \cos \angle BEC = BC^2.</cmath>
 
−
Because <math>\cos \angle AEB = \cos \theta</math> and <math>BC = 6</math>, we have <cmath>b^2 + c^2 - 2 b c \cos \theta  = 6^2. \ \ \ (3)</cmath>
 
−
In <math>\triangle CED</math>, following from the law of cosines, we have <cmath>c^2 + d^2 - 2  c d \cos \angle CED= CD^2.</cmath>
 
−
Because <math>\cos \angle CED = \cos \left(180^\circ - \theta \right) = \cos \theta</math> and <math>CD = 9</math>, we have <cmath>c^2 + d^2 + 2 c d \cos \theta = 9^2. \ \ \ (4)</cmath>
 
−
In <math>\triangle DEA</math>, following from the law of cosines, we have <cmath>d^2 + a^2 - 2 d a \cos \angle DEA = DA^2.</cmath>
 
−
Because <math>\cos \angle DEC = \cos \theta</math> and <math>DA = 7</math>, we have <cmath>d^2 + a^2 - 2 d a \cos \theta  = 7^2. \ \ \ (5)</cmath>
 
−
By taking <math>\frac{1}{2} \left( {\rm Eq} \ (2) - {\rm Eq} \ (3) + {\rm Eq} \ (4) - {\rm Eq} \ (5) \right)</math>, we get <cmath>\left( ab + bc + cd + da \right) \cos \theta = \frac{21}{2}. \ \ \ (6)</cmath>
 
−
By taking <math>\frac{{\rm Eq} \ (1)}{{\rm Eq} \ (6)}</math>, we get <cmath>\tan \theta = \frac{60}{21/2} = \frac{40}{7}.</cmath>
 
−
Therefore, by writing this answer in the form of <math>\frac{m}{n}</math>, we have <math>m = 40</math> and <math>n = 7</math>.
 
−
 
−
Therefore, the answer to this question is <math>m + n = 40 + 7 = \boxed{047}</math>.
 
−
 
−
~ Steven Chen (www.professorchenedu.com)
 
−
 
−
===Solution 1.2 (Version 2)===
 
 
Since we are asked to find <math>\tan \theta</math>, we can find <math>\sin \theta</math> and <math>\cos \theta</math> separately and use their values to get <math>\tan \theta</math>. We can start by drawing a diagram. Let the vertices of the quadrilateral be <math>A</math>, <math>B</math>, <math>C</math>, and <math>D</math>. Let <math>AB = 5</math>, <math>BC = 6</math>, <math>CD = 9</math>, and <math>DA = 7</math>. Let <math>AX = a</math>, <math>BX = b</math>, <math>CX = c</math>, and <math>DX = d</math>. We know that <math>\theta</math> is the acute angle formed between the intersection of the diagonals <math>AC</math> and <math>BD</math>.
 
Since we are asked to find <math>\tan \theta</math>, we can find <math>\sin \theta</math> and <math>\cos \theta</math> separately and use their values to get <math>\tan \theta</math>. We can start by drawing a diagram. Let the vertices of the quadrilateral be <math>A</math>, <math>B</math>, <math>C</math>, and <math>D</math>. Let <math>AB = 5</math>, <math>BC = 6</math>, <math>CD = 9</math>, and <math>DA = 7</math>. Let <math>AX = a</math>, <math>BX = b</math>, <math>CX = c</math>, and <math>DX = d</math>. We know that <math>\theta</math> is the acute angle formed between the intersection of the diagonals <math>AC</math> and <math>BD</math>.
 
<asy>
 
<asy>
Line 98: Line 51:
 
7^2 &= d^2 + a^2 - 2da\cos \theta.   
 
7^2 &= d^2 + a^2 - 2da\cos \theta.   
 
\end{align*}</cmath>
 
\end{align*}</cmath>
−
We know that <math>\cos (180^\circ - \theta) = -\cos \theta</math>. We can substitute this value into our equations to get:
+
We know that <math>\cos (180^\circ - \theta) = -\cos \theta</math> for all <math>\theta</math>. We can substitute this value into our equations to get:
 
<cmath>\begin{align*}   
 
<cmath>\begin{align*}   
−
5^2 &= a^2 + b^2 + 2ab\cos \theta, \\   
+
5^2 &= a^2 + b^2 + 2ab\cos \theta, &&(1) \\   
−
6^2 &= b^2 + c^2 - 2bc\cos \theta, \\   
+
6^2 &= b^2 + c^2 - 2bc\cos \theta, &&(2) \\   
−
9^2 &= c^2 + d^2 + 2cd\cos \theta, \\   
+
9^2 &= c^2 + d^2 + 2cd\cos \theta, &&(3) \\   
−
7^2 &= d^2 + a^2 - 2da\cos \theta.
+
7^2 &= d^2 + a^2 - 2da\cos \theta. &&(4)
 
\end{align*}</cmath>
 
\end{align*}</cmath>
−
If we subtract the sum of the first and third equation from the sum of the second and fourth equation, the squared terms cancel, leaving us with:
+
If we subtract <math>(2)+(4)</math> from <math>(1)+(3)</math>, the squared terms cancel, leaving us with:
 
<cmath>\begin{align*}
 
<cmath>\begin{align*}
 
5^2 + 9^2 - 6^2 - 7^2 &= 2ab \cos \theta + 2bc \cos \theta + 2cd \cos \theta + 2da \cos \theta \\  
 
5^2 + 9^2 - 6^2 - 7^2 &= 2ab \cos \theta + 2bc \cos \theta + 2cd \cos \theta + 2da \cos \theta \\  
Line 114: Line 67:
 
Since we have figured out <math>\sin \theta</math> and <math>\cos \theta</math>, we can calculate <math>\tan \theta</math>: <cmath>\tan \theta = \frac{\sin \theta}{\cos \theta} = \frac{\frac{60}{ab + bc + cd + da}}{\frac{21/2}{ab + bc + cd + da}} = \frac{60}{21/2} = \frac{120}{21} = \frac{40}{7}.</cmath>
 
Since we have figured out <math>\sin \theta</math> and <math>\cos \theta</math>, we can calculate <math>\tan \theta</math>: <cmath>\tan \theta = \frac{\sin \theta}{\cos \theta} = \frac{\frac{60}{ab + bc + cd + da}}{\frac{21/2}{ab + bc + cd + da}} = \frac{60}{21/2} = \frac{120}{21} = \frac{40}{7}.</cmath>
 
Therefore our answer is <math>40 + 7 = \boxed{047}</math>.
 
Therefore our answer is <math>40 + 7 = \boxed{047}</math>.
 +
 +
~ Steven Chen (www.professorchenedu.com)
  
 
~ my_aops_lessons
 
~ my_aops_lessons
  
−
==Solution 2 (Pythagorean Theorem)==
+
==Solution 2 (Right Triangles)==
−
This solution refers to the <b>Diagram</b> section.
+
In convex quadrilateral <math>ABCD,</math> let <math>AB=5,BC=6,CD=9,</math> and <math>DA=7.</math> Let <math>A'</math> and <math>C'</math> be the feet of the perpendiculars from <math>A</math> and <math>C,</math> respectively, to <math>\overline{BD}.</math> We obtain the following diagram:
 +
<asy>
 +
/* Made by MRENTHUSIASM */
 +
size(500);
  
−
In convex quadrilateral <math>ABCD,</math> let <math>AB=5,BC=6,CD=9,</math> and <math>DA=7.</math> Let <math>A'</math> and <math>C'</math> be the feet of the perpendiculars from <math>A</math> and <math>C,</math> respectively, to <math>\overline{BD}.</math> We obtain the following diagram:
+
pair A, B, C, D, P, A1, C1;
−
[[File:2021 AIME II Problem 12 Solution.png|center]]
+
B = origin;
−
Let <math>BC'=p,C'E=q,EA'=r,A'D=s,AA'=h_1,</math> and <math>CC'=h_2.</math> Applying the Pythagorean Theorem to right triangles <math>\triangle ABA',\triangle BCC',\triangle CDC',</math> and <math>\triangle DAA',</math> we respectively get
+
D = (3*sqrt(32498*(29400*sqrt(47)+312523))/32498,0);
 +
A = intersectionpoints(Circle(B,5),Circle(D,7))[0];
 +
C = intersectionpoints(Circle(B,6),Circle(D,9))[1];
 +
P = intersectionpoint(A--C,B--D);
 +
A1 = foot(A,B,D);
 +
C1 = foot(C,B,D);
 +
markscalefactor=3/160;
 +
draw(rightanglemark(A,A1,D),red);
 +
draw(rightanglemark(C,C1,B),red);
 +
dot("$A$",A,1.5*dir(aCos(7/sqrt(1649))));
 +
dot("$B$",B,1.5*W);
 +
dot("$C$",C,1.5*dir(180+aCos(7/sqrt(1649))));
 +
dot("$D$",D,1.5*E);
 +
dot("$E$",P,dir(180-(180-aCos(7/sqrt(1649)))/2));
 +
dot("$A'$",A1,dir(-75));
 +
dot("$C'$",C1,N);
 +
label("$\theta$",P,dir(180+aCos(7/sqrt(1649))/2),red);
 +
draw(A--A1^^C--C1,dashed);
 +
draw(A--B--C--D--cycle^^A--C^^B--D);
 +
</asy>
 +
Let <math>BC'=p,C'E=q,EA'=r,A'D=s,AA'=h_1,</math> and <math>CC'=h_2.</math> We apply the Pythagorean Theorem to right triangles <math>\triangle ABA',\triangle BCC',\triangle CDC',</math> and <math>\triangle DAA',</math> respectively:
 
<cmath>\begin{array}{ccccccccccccccccc}
 
<cmath>\begin{array}{ccccccccccccccccc}
 
(p+q+r)^2&+&h_1^2&=&5^2, &&&&&&&&&&&&\hspace{36mm}(1) \\ [1ex]
 
(p+q+r)^2&+&h_1^2&=&5^2, &&&&&&&&&&&&\hspace{36mm}(1) \\ [1ex]
Line 153: Line 131:
 
<cmath>\begin{align*}
 
<cmath>\begin{align*}
 
\frac{h_1+h_2}{q+r}&=\frac{40}{7} \\
 
\frac{h_1+h_2}{q+r}&=\frac{40}{7} \\
−
\frac{\overbrace{r\tan\theta}^{\text{by }(1\star).}+\overbrace{q\tan\theta}^{\text{by }(2\star).}}{q+r}&=\frac{40}{7} \\
+
\frac{r\tan\theta+q\tan\theta}{q+r}&=\frac{40}{7} \hspace{15mm} &&\text{by }(1\star)\text{ and }(2\star)\\
 
\frac{(r+q)\tan\theta}{q+r}&=\frac{40}{7} \\
 
\frac{(r+q)\tan\theta}{q+r}&=\frac{40}{7} \\
 
\tan\theta&=\frac{40}{7},
 
\tan\theta&=\frac{40}{7},
Line 160: Line 138:
  
 
~MRENTHUSIASM
 
~MRENTHUSIASM
 +
 +
==Solution 3 (Bretschneider's Formula)==
 +
 +
===Bretschneider's Formula===
 +
 +
<asy> size(200); import olympiad; defaultpen(linewidth(0.8)+fontsize(10));
 +
pair A,B,C,D;
 +
A=origin; B=(1.25,0); D=dir(65); C=D+0.85*dir(90)*(A-D);
 +
draw(A--B--C--D--cycle); draw(A--C^^B--D, gray+0.5);
 +
dot("$A$", A, SW); dot("$B$", B, SE); dot("$C$", C, NE); dot("$D$",D,NW);
 +
label("$a$", A--B, S); label("$b$", B--C, E); label("$c$", D--C, N); label("$d$",D--A,W); label("$u$",D--B,2*dir(170)); label("$v$",A--C,S);
 +
</asy>
 +
Given quadrilateral <math>ABCD</math>, let, <math>a, b, c, d</math>, be the sides, <math>s</math> the semiperimeter, and <math>u, v</math>, the diagonals. Then the area, <math>K</math>, is given by <cmath>K = \tfrac 14 \sqrt {4u^2v^2-(b^2+d^2-a^2-c^2)^2}</cmath>
 +
 +
===Solution===
 +
By Bretschneider's Formula, <cmath>30=\tfrac{1}{4}\sqrt{4u^2v^2-(b^2+d^2-a^2-c^2)^2}=\tfrac{1}{4}\sqrt{4u^2v^2-441}.</cmath> Thus, <math>uv=3\sqrt{1649}</math>. Also, <cmath>[ABCD]=\tfrac 12 \cdot uv\sin{\theta};</cmath> solving for <math>\sin{\theta}</math> yields <math>\sin{\theta}=\tfrac{40}{\sqrt{1649}}</math>. Since <math>\theta</math> is acute, <math>\cos{\theta}</math> is positive, from which <math>\cos{\theta}=\tfrac{7}{\sqrt{1649}}</math>. Solving for <math>\tan{\theta}</math> yields <cmath>\tan{\theta}=\frac{\sin{\theta}}{\cos{\theta}}=\frac{40}{7},</cmath> for a final answer of <math>\boxed{047}</math>.
 +
 +
~ Leo.Euler
 +
 +
==Solution 4 (Symmetry)==
 +
[[File:AIME-I-2021-12.png|350px|right]]
 +
<i><b>Claim</b></i>
 +
 +
Given an inscribed quadrilateral <math>ABCD</math> with sides <math>AB = a, BC = b, CD = c,</math> and <math>DA = d.</math> Prove that the <math>\angle \theta < 90^\circ</math> between the diagonals is given by
 +
<cmath>\begin{align*}2(ac + bd) \cos \theta =  {|d^2 – c^2 + b^2 – a^2|}.\end{align*}</cmath>
 +
<i><b>Proof</b></i>
 +
 +
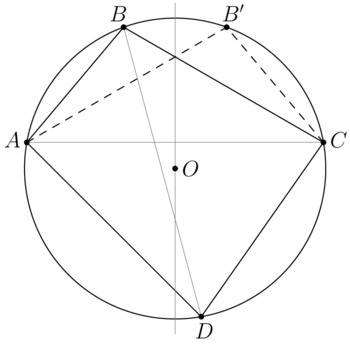
Let the point <math>B'</math> be symmetric to <math>B</math> with respect to the perpendicular bisector <math>AC.</math> Then the quadrilateral <math>AB'CD</math> is an inscribed one, <math>AB' = b, B'C = a.</math>
 +
 +
<cmath> 2 \angle AEB = \overset{\Large\frown} {AB}  + \overset{\Large\frown} {CD}.</cmath>
 +
<cmath>\begin{align*} 2\angle B'AD = \overset{\Large\frown} {B'C} + \overset{\Large\frown} {CD} = \overset{\Large\frown} {AB} + \overset{\Large\frown} {CD} \implies \angle AEB = \angle B'AD.\end{align*}</cmath>
 +
 +
We apply the Law of Cosines to <math>\triangle AB'D</math> and <math>\triangle CB'D</math>:
 +
<cmath>\begin{align*} B'D^2 = AD^2 + AB'^2 – 2 AD \cdot AB' \cos \theta, \end{align*}</cmath>
 +
<cmath>\begin{align*} B'D^2 = CD^2 + CB'^2 + 2 CD \cdot CB' \cos \theta,\end{align*}</cmath>
 +
<cmath>\begin{align*} d^2 + b^2 – 2 bd \cos \theta = c^2 + a^2 + 2ac \cos \theta,\end{align*}</cmath>
 +
<cmath>\begin{align*} 2(ac + bd) \cos \theta = |d^2 – c^2 + b^2 – a^2|.\end{align*}</cmath>
 +
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
 +
==Note 1==
 +
By generalization, the tangent of the acute angle formed by the diagonals is <cmath>\left|\frac{4A}{a^2-b^2+c^2-d^2}\right|.</cmath>
 +
 +
==Video Solution by MOP 2024==
 +
https://youtu.be/K0u0ACMTSw8
 +
 +
~r00tsOfUnity
  
 
==Video Solution==
 
==Video Solution==
 
https://www.youtube.com/watch?v=7DxIdTLNbo0
 
https://www.youtube.com/watch?v=7DxIdTLNbo0
  
−
==See also==
+
==Video Solution by Interstigation==
 +
https://youtu.be/8GRO4za5rPI
 +
 
 +
~Interstigation
 +
 
 +
==See Also==
 
{{AIME box|year=2021|n=II|num-b=11|num-a=13}}
 
{{AIME box|year=2021|n=II|num-b=11|num-a=13}}
 
{{MAA Notice}}
 
{{MAA Notice}}

Latest revision as of 16:33, 12 January 2024

Problem

A convex quadrilateral has area $30$ and side lengths $5, 6, 9,$ and $7,$ in that order. Denote by $\theta$ the measure of the acute angle formed by the diagonals of the quadrilateral. Then $\tan \theta$ can be written in the form $\tfrac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. Find $m + n$.

Solution 1 (Sines and Cosines)

Since we are asked to find $\tan \theta$, we can find $\sin \theta$ and $\cos \theta$ separately and use their values to get $\tan \theta$. We can start by drawing a diagram. Let the vertices of the quadrilateral be $A$, $B$, $C$, and $D$. Let $AB = 5$, $BC = 6$, $CD = 9$, and $DA = 7$. Let $AX = a$, $BX = b$, $CX = c$, and $DX = d$. We know that $\theta$ is the acute angle formed between the intersection of the diagonals $AC$ and $BD$. [asy] unitsize(4cm); pair A,B,C,D,X; A = (0,0); B = (1,0); C = (1.25,-1); D = (-0.75,-0.75); draw(A--B--C--D--cycle,black+1bp); X = intersectionpoint(A--C,B--D); draw(A--C); draw(B--D); label("$A$",A,NW); label("$B$",B,NE); label("$C$",C,SE); label("$D$",D,SW); dot(X); label("$X$",X,S); label("$5$",(A+B)/2,N); label("$6$",(B+C)/2,E); label("$9$",(C+D)/2,S); label("$7$",(D+A)/2,W); label("$\theta$",X,2.5E); label("$a$",(A+X)/2,NE); label("$b$",(B+X)/2,NW); label("$c$",(C+X)/2,SW); label("$d$",(D+X)/2,SE); [/asy] We are given that the area of quadrilateral $ABCD$ is $30$. We can express this area using the areas of triangles $AXB$, $BXC$, $CXD$, and $DXA$. Since we want to find $\sin \theta$ and $\cos \theta$, we can represent these areas using $\sin \theta$ as follows: \begin{align*} 30 &=[ABCD] \\ &=[AXB] + [BXC] + [CXD] + [DXA] \\ &=\frac{1}{2} ab \sin (\angle AXB) + \frac{1}{2} bc \sin (\angle BXC) + \frac{1}{2} cd \sin (\angle CXD) + \frac{1}{2} da \sin (\angle AXD) \\ &=\frac{1}{2} ab \sin (180^\circ - \theta) + \frac{1}{2} bc \sin (\theta) + \frac{1}{2} cd \sin (180^\circ - \theta) + \frac{1}{2} da \sin (\theta). \end{align*} We know that $\sin (180^\circ - \theta) = \sin \theta$. Therefore it follows that: \begin{align*} 30 &=\frac{1}{2} ab \sin (180^\circ - \theta) + \frac{1}{2} bc \sin (\theta) + \frac{1}{2} cd \sin (180^\circ - \theta) + \frac{1}{2} da \sin (\theta) \\ &=\frac{1}{2} ab \sin (\theta) + \frac{1}{2} bc \sin (\theta) + \frac{1}{2} cd \sin (\theta) + \frac{1}{2} da \sin (\theta) \\ &=\frac{1}{2}\sin\theta (ab + bc + cd + da). \end{align*} From here we see that $\sin \theta = \frac{60}{ab + bc + cd + da}$. Now we need to find $\cos \theta$. Using the Law of Cosines on each of the four smaller triangles, we get following equations: \begin{align*} 5^2 &= a^2 + b^2 - 2ab\cos(180^\circ-\theta), \\ 6^2 &= b^2 + c^2 - 2bc\cos \theta, \\ 9^2 &= c^2 + d^2 - 2cd\cos(180^\circ-\theta), \\ 7^2 &= d^2 + a^2 - 2da\cos \theta. \end{align*} We know that $\cos (180^\circ - \theta) = -\cos \theta$ for all $\theta$. We can substitute this value into our equations to get: \begin{align*} 5^2 &= a^2 + b^2 + 2ab\cos \theta, &&(1) \\ 6^2 &= b^2 + c^2 - 2bc\cos \theta, &&(2) \\ 9^2 &= c^2 + d^2 + 2cd\cos \theta, &&(3) \\ 7^2 &= d^2 + a^2 - 2da\cos \theta. &&(4) \end{align*} If we subtract $(2)+(4)$ from $(1)+(3)$, the squared terms cancel, leaving us with: \begin{align*} 5^2 + 9^2 - 6^2 - 7^2 &= 2ab \cos \theta + 2bc \cos \theta + 2cd \cos \theta + 2da \cos \theta \\ 21 &= 2\cos \theta (ab + bc + cd + da). \end{align*} From here we see that $\cos \theta = \frac{21/2}{ab + bc + cd + da}$.

Since we have figured out $\sin \theta$ and $\cos \theta$, we can calculate $\tan \theta$: \[\tan \theta = \frac{\sin \theta}{\cos \theta} = \frac{\frac{60}{ab + bc + cd + da}}{\frac{21/2}{ab + bc + cd + da}} = \frac{60}{21/2} = \frac{120}{21} = \frac{40}{7}.\] Therefore our answer is $40 + 7 = \boxed{047}$.

~ Steven Chen (www.professorchenedu.com)

~ my_aops_lessons

Solution 2 (Right Triangles)

In convex quadrilateral $ABCD,$ let $AB=5,BC=6,CD=9,$ and $DA=7.$ Let $A'$ and $C'$ be the feet of the perpendiculars from $A$ and $C,$ respectively, to $\overline{BD}.$ We obtain the following diagram: [asy] /* Made by MRENTHUSIASM */ size(500); pair A, B, C, D, P, A1, C1; B = origin; D = (3*sqrt(32498*(29400*sqrt(47)+312523))/32498,0); A = intersectionpoints(Circle(B,5),Circle(D,7))[0]; C = intersectionpoints(Circle(B,6),Circle(D,9))[1]; P = intersectionpoint(A--C,B--D); A1 = foot(A,B,D); C1 = foot(C,B,D); markscalefactor=3/160; draw(rightanglemark(A,A1,D),red); draw(rightanglemark(C,C1,B),red); dot("$A$",A,1.5*dir(aCos(7/sqrt(1649)))); dot("$B$",B,1.5*W); dot("$C$",C,1.5*dir(180+aCos(7/sqrt(1649)))); dot("$D$",D,1.5*E); dot("$E$",P,dir(180-(180-aCos(7/sqrt(1649)))/2)); dot("$A'$",A1,dir(-75)); dot("$C'$",C1,N); label("$\theta$",P,dir(180+aCos(7/sqrt(1649))/2),red); draw(A--A1^^C--C1,dashed); draw(A--B--C--D--cycle^^A--C^^B--D); [/asy] Let $BC'=p,C'E=q,EA'=r,A'D=s,AA'=h_1,$ and $CC'=h_2.$ We apply the Pythagorean Theorem to right triangles $\triangle ABA',\triangle BCC',\triangle CDC',$ and $\triangle DAA',$ respectively: \[\begin{array}{ccccccccccccccccc} (p+q+r)^2&+&h_1^2&=&5^2, &&&&&&&&&&&&\hspace{36mm}(1) \\ [1ex] p^2&+&h_2^2&=&6^2, &&&&&&&&&&&&\hspace{36mm}(2) \\ [1ex] (q+r+s)^2&+&h_2^2&=&9^2, &&&&&&&&&&&&\hspace{36mm}(3) \\ [1ex] s^2&+&h_1^2&=&7^2. &&&&&&&&&&&&\hspace{36mm}(4) \end{array}\] Let the brackets denote areas. We get \begin{align*} [ABD]+[CBD]&=[ABCD] \\ \frac12(p+q+r+s)h_1+\frac12(p+q+r+s)h_2&=30 \\ \frac12(p+q+r+s)(h_1+h_2)&=30 \\ (p+q+r+s)(h_1+h_2)&=60. \hspace{49.25mm}(5) \end{align*} We subtract $(2)+(4)$ from $(1)+(3):$ \begin{align*} (p+q+r)^2+(q+r+s)^2-p^2-s^2&=21 \\ \left[(p+q+r)^2-s^2\right]+\left[(q+r+s)^2-p^2\right]&=21 \\ (p+q+r+s)(p+q+r-s)+(p+q+r+s)(-p+q+r+s)&=21 \\ (p+q+r+s)(2q+2r)&=21 \\ 2(p+q+r+s)(q+r)&=21 \\ (p+q+r+s)(q+r)&=\frac{21}{2}. \hspace{9.5mm}(6) \end{align*} From right triangles $\triangle AEA'$ and $\triangle CEC',$ we have $\tan\theta=\frac{h_1}{r}=\frac{h_2}{q}.$ It follows that \begin{alignat*}{8} \tan\theta&=\frac{h_1}{r}\qquad&\implies\qquad h_1&=r\tan\theta, \hspace{64mm}&(1\star)\\ \tan\theta&=\frac{h_2}{q}\qquad&\implies\qquad h_2&=q\tan\theta. &(2\star) \end{alignat*} Finally, we divide $(5)$ by $(6):$ \begin{align*} \frac{h_1+h_2}{q+r}&=\frac{40}{7} \\ \frac{r\tan\theta+q\tan\theta}{q+r}&=\frac{40}{7} \hspace{15mm} &&\text{by }(1\star)\text{ and }(2\star)\\ \frac{(r+q)\tan\theta}{q+r}&=\frac{40}{7} \\ \tan\theta&=\frac{40}{7}, \end{align*} from which the answer is $40+7=\boxed{047}.$

~MRENTHUSIASM

Solution 3 (Bretschneider's Formula)

Bretschneider's Formula

[asy] size(200); import olympiad; defaultpen(linewidth(0.8)+fontsize(10)); pair A,B,C,D; A=origin; B=(1.25,0); D=dir(65); C=D+0.85*dir(90)*(A-D); draw(A--B--C--D--cycle); draw(A--C^^B--D, gray+0.5); dot("$A$", A, SW); dot("$B$", B, SE); dot("$C$", C, NE); dot("$D$",D,NW); label("$a$", A--B, S); label("$b$", B--C, E); label("$c$", D--C, N); label("$d$",D--A,W); label("$u$",D--B,2*dir(170)); label("$v$",A--C,S); [/asy] Given quadrilateral $ABCD$, let, $a, b, c, d$, be the sides, $s$ the semiperimeter, and $u, v$, the diagonals. Then the area, $K$, is given by \[K = \tfrac 14 \sqrt {4u^2v^2-(b^2+d^2-a^2-c^2)^2}\]

Solution

By Bretschneider's Formula, \[30=\tfrac{1}{4}\sqrt{4u^2v^2-(b^2+d^2-a^2-c^2)^2}=\tfrac{1}{4}\sqrt{4u^2v^2-441}.\] Thus, $uv=3\sqrt{1649}$. Also, \[[ABCD]=\tfrac 12 \cdot uv\sin{\theta};\] solving for $\sin{\theta}$ yields $\sin{\theta}=\tfrac{40}{\sqrt{1649}}$. Since $\theta$ is acute, $\cos{\theta}$ is positive, from which $\cos{\theta}=\tfrac{7}{\sqrt{1649}}$. Solving for $\tan{\theta}$ yields \[\tan{\theta}=\frac{\sin{\theta}}{\cos{\theta}}=\frac{40}{7},\] for a final answer of $\boxed{047}$.

~ Leo.Euler

Solution 4 (Symmetry)

AIME-I-2021-12.png

Claim

Given an inscribed quadrilateral $ABCD$ with sides $AB = a, BC = b, CD = c,$ and $DA = d.$ Prove that the $\angle \theta < 90^\circ$ between the diagonals is given by \begin{align*}2(ac + bd) \cos \theta = {|d^2 – c^2 + b^2 – a^2|}.\end{align*} Proof

Let the point $B'$ be symmetric to $B$ with respect to the perpendicular bisector $AC.$ Then the quadrilateral $AB'CD$ is an inscribed one, $AB' = b, B'C = a.$

\[2 \angle AEB = \overset{\Large\frown} {AB} + \overset{\Large\frown} {CD}.\] \begin{align*} 2\angle B'AD = \overset{\Large\frown} {B'C} + \overset{\Large\frown} {CD} = \overset{\Large\frown} {AB} + \overset{\Large\frown} {CD} \implies \angle AEB = \angle B'AD.\end{align*}

We apply the Law of Cosines to $\triangle AB'D$ and $\triangle CB'D$: \begin{align*} B'D^2 = AD^2 + AB'^2 – 2 AD \cdot AB' \cos \theta, \end{align*} \begin{align*} B'D^2 = CD^2 + CB'^2 + 2 CD \cdot CB' \cos \theta,\end{align*} \begin{align*} d^2 + b^2 – 2 bd \cos \theta = c^2 + a^2 + 2ac \cos \theta,\end{align*} \begin{align*} 2(ac + bd) \cos \theta = |d^2 – c^2 + b^2 – a^2|.\end{align*}

vladimir.shelomovskii@gmail.com, vvsss

Note 1

By generalization, the tangent of the acute angle formed by the diagonals is \[\left|\frac{4A}{a^2-b^2+c^2-d^2}\right|.\]

Video Solution by MOP 2024

https://youtu.be/K0u0ACMTSw8

~r00tsOfUnity

Video Solution

https://www.youtube.com/watch?v=7DxIdTLNbo0

Video Solution by Interstigation

https://youtu.be/8GRO4za5rPI

~Interstigation

See Also

2021 AIME II (Problems • Answer Key • Resources)
Preceded by
Problem 11 		Followed by
Problem 13
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2021_AIME_II_Problems/Problem_12&oldid=210539"