Difference between revisions of "2021 AIME I Problems/Problem 11"
MRENTHUSIASM (talk | contribs) m (→Remark (Ptolemy's Theorem)) |
Math-titan (talk | contribs) (→Solution 3 (Pythagorean Theorem)) |
||
| (40 intermediate revisions by 5 users not shown) | |||
| Line 3: | Line 3: | ||
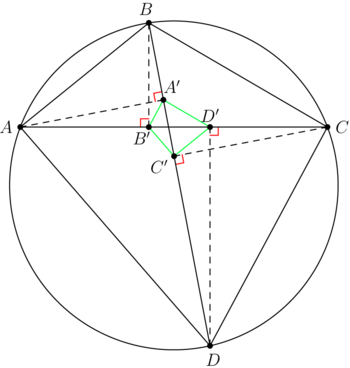
==Diagram== | ==Diagram== | ||
| − | + | <asy> | |
| + | /* Made by MRENTHUSIASM */ | ||
| + | size(300); | ||
| − | + | pair A, B, C, D, A1, B1, C1, D1; | |
| − | + | A = origin; | |
| − | = | + | C = (sqrt(53041)/31,0); |
| − | + | B = intersectionpoints(Circle(A,4),Circle(C,5))[0]; | |
| − | + | D = intersectionpoints(Circle(A,7),Circle(C,6))[1]; | |
| − | + | A1 = foot(A,B,D); | |
| − | + | C1 = foot(C,B,D); | |
| − | + | B1 = foot(B,A,C); | |
| − | + | D1 = foot(D,A,C); | |
| − | + | markscalefactor=0.025; | |
| + | draw(rightanglemark(A,A1,B),red); | ||
| + | draw(rightanglemark(B,B1,A),red); | ||
| + | draw(rightanglemark(C,C1,D),red); | ||
| + | draw(rightanglemark(D,D1,C),red); | ||
| + | draw(A1--B1--C1--D1--cycle,green); | ||
| + | dot("$A$",A,1.5*W,linewidth(4)); | ||
| + | dot("$B$",B,1.5*dir(180-aCos(11/59)),linewidth(4)); | ||
| + | dot("$C$",C,1.5*E,linewidth(4)); | ||
| + | dot("$D$",D,1.5*dir(-aCos(11/59)),linewidth(4)); | ||
| + | dot("$A_1$",A1,1.5*dir(A1-A),linewidth(4)); | ||
| + | dot("$B_1$",B1,1.5*S,linewidth(4)); | ||
| + | dot("$C_1$",C1,1.5*dir(C1-C),linewidth(4)); | ||
| + | dot("$D_1$",D1,1.5*N,linewidth(4)); | ||
| + | draw(A--B--C--D--cycle^^A--C^^B--D^^circumcircle(A,B,C)); | ||
| + | draw(A--A1^^B--B1^^C--C1^^D--D1,dashed); | ||
| + | </asy> | ||
| + | ~MRENTHUSIASM | ||
| − | ==Solution | + | ==Solution 1 (Cyclic Quadrilaterals, Similar Triangles, and Trigonometry)== |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
This solution refers to the <b>Diagram</b> section. | This solution refers to the <b>Diagram</b> section. | ||
| Line 39: | Line 43: | ||
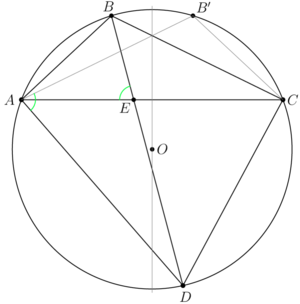
We obtain the following diagram: | We obtain the following diagram: | ||
| − | [[ | + | <asy> |
| + | /* Made by MRENTHUSIASM */ | ||
| + | size(300); | ||
| + | |||
| + | pair A, B, C, D, A1, B1, C1, D1, P, M1, M2; | ||
| + | A = origin; | ||
| + | C = (sqrt(53041)/31,0); | ||
| + | B = intersectionpoints(Circle(A,4),Circle(C,5))[0]; | ||
| + | D = intersectionpoints(Circle(A,7),Circle(C,6))[1]; | ||
| + | A1 = foot(A,B,D); | ||
| + | C1 = foot(C,B,D); | ||
| + | B1 = foot(B,A,C); | ||
| + | D1 = foot(D,A,C); | ||
| + | P = intersectionpoint(A--C,B--D); | ||
| + | M1 = midpoint(A--B); | ||
| + | M2 = midpoint(C--D); | ||
| + | markscalefactor=0.025; | ||
| + | draw(rightanglemark(A,A1,B),red); | ||
| + | draw(rightanglemark(B,B1,A),red); | ||
| + | draw(rightanglemark(C,C1,D),red); | ||
| + | draw(rightanglemark(D,D1,C),red); | ||
| + | draw(Arc(M1,A,B)^^Arc(M2,C,D),blue); | ||
| + | draw(A1--B1--C1--D1--cycle,green); | ||
| + | dot("$A$",A,1.5*W,linewidth(4)); | ||
| + | dot("$B$",B,1.5*dir(180-aCos(11/59)),linewidth(4)); | ||
| + | dot("$C$",C,1.5*E,linewidth(4)); | ||
| + | dot("$D$",D,1.5*dir(-aCos(11/59)),linewidth(4)); | ||
| + | dot("$A_1$",A1,1.5*dir(A1-A),linewidth(4)); | ||
| + | dot("$B_1$",B1,1.5*S,linewidth(4)); | ||
| + | dot("$C_1$",C1,1.5*dir(C1-C),linewidth(4)); | ||
| + | dot("$D_1$",D1,1.5*N,linewidth(4)); | ||
| + | dot("$E$",P,dir((180-aCos(11/59))/2),linewidth(4)); | ||
| + | label("$\theta$",P,dir(180-aCos(11/59)/2),red); | ||
| + | draw(A--B--C--D--cycle^^A--C^^B--D^^circumcircle(A,B,C)); | ||
| + | draw(A--A1^^B--B1^^C--C1^^D--D1,dashed); | ||
| + | </asy> | ||
In every cyclic quadrilateral, each pair of opposite angles is supplementary. So, we have <math>\angle EA_1B_1=\angle EAB</math> (both supplementary to <math>\angle B_1A_1B</math>) and <math>\angle EB_1A_1=\angle EBA</math> (both supplementary to <math>\angle A_1B_1A</math>), from which <math>\triangle A_1B_1E \sim \triangle ABE</math> by AA, with the ratio of similitude <cmath>\frac{A_1B_1}{AB}=\underbrace{\frac{A_1E}{AE}}_{\substack{\text{right} \\ \triangle A_1AE}}=\underbrace{\frac{B_1E}{BE}}_{\substack{\text{right} \\ \triangle B_1BE}}=\cos\theta. \hspace{15mm}(1)</cmath> | In every cyclic quadrilateral, each pair of opposite angles is supplementary. So, we have <math>\angle EA_1B_1=\angle EAB</math> (both supplementary to <math>\angle B_1A_1B</math>) and <math>\angle EB_1A_1=\angle EBA</math> (both supplementary to <math>\angle A_1B_1A</math>), from which <math>\triangle A_1B_1E \sim \triangle ABE</math> by AA, with the ratio of similitude <cmath>\frac{A_1B_1}{AB}=\underbrace{\frac{A_1E}{AE}}_{\substack{\text{right} \\ \triangle A_1AE}}=\underbrace{\frac{B_1E}{BE}}_{\substack{\text{right} \\ \triangle B_1BE}}=\cos\theta. \hspace{15mm}(1)</cmath> | ||
Similarly, we have <math>\angle EC_1D_1=\angle ECD</math> (both supplementary to <math>\angle D_1C_1D</math>) and <math>\angle ED_1C_1=\angle EDC</math> (both supplementary to <math>\angle C_1D_1C</math>), from which <math>\triangle C_1D_1E \sim \triangle CDE</math> by AA, with the ratio of similitude <cmath>\frac{C_1D_1}{CD}=\underbrace{\frac{C_1E}{CE}}_{\substack{\text{right} \\ \triangle C_1CE}}=\underbrace{\frac{D_1E}{DE}}_{\substack{\text{right} \\ \triangle D_1DE}}=\cos\theta. \hspace{14.75mm}(2)</cmath> | Similarly, we have <math>\angle EC_1D_1=\angle ECD</math> (both supplementary to <math>\angle D_1C_1D</math>) and <math>\angle ED_1C_1=\angle EDC</math> (both supplementary to <math>\angle C_1D_1C</math>), from which <math>\triangle C_1D_1E \sim \triangle CDE</math> by AA, with the ratio of similitude <cmath>\frac{C_1D_1}{CD}=\underbrace{\frac{C_1E}{CE}}_{\substack{\text{right} \\ \triangle C_1CE}}=\underbrace{\frac{D_1E}{DE}}_{\substack{\text{right} \\ \triangle D_1DE}}=\cos\theta. \hspace{14.75mm}(2)</cmath> | ||
| Line 55: | Line 94: | ||
Two solutions follow from here: | Two solutions follow from here: | ||
| − | ===Solution | + | ===Solution 1.1 (Law of Cosines)=== |
Note that <math>\cos(180^\circ-\theta)=-\cos\theta</math> holds for all <math>\theta.</math> We apply the Law of Cosines to <math>\triangle ABE, \triangle BCE, \triangle CDE,</math> and <math>\triangle DAE,</math> respectively: | Note that <math>\cos(180^\circ-\theta)=-\cos\theta</math> holds for all <math>\theta.</math> We apply the Law of Cosines to <math>\triangle ABE, \triangle BCE, \triangle CDE,</math> and <math>\triangle DAE,</math> respectively: | ||
<cmath>\begin{alignat*}{12} | <cmath>\begin{alignat*}{12} | ||
| Line 72: | Line 111: | ||
Finally, substituting this result into <math>(\bigstar)</math> gives <math>22\cos\theta=\frac{242}{59},</math> from which the answer is <math>242+59=\boxed{301}.</math> | Finally, substituting this result into <math>(\bigstar)</math> gives <math>22\cos\theta=\frac{242}{59},</math> from which the answer is <math>242+59=\boxed{301}.</math> | ||
| − | ~MRENTHUSIASM ( | + | ~MRENTHUSIASM (credit given to Math Jams's <b>2021 AIME I Discussion</b>) |
| − | ===Solution | + | ===Solution 1.2 (Area Formulas)=== |
Let the brackets denote areas. | Let the brackets denote areas. | ||
We find <math>[ABCD]</math> in two different ways: | We find <math>[ABCD]</math> in two different ways: | ||
| Line 92: | Line 131: | ||
Finally, substituting this result into <math>(\bigstar)</math> gives <math>22\cos\theta=\frac{242}{59},</math> from which the answer is <math>242+59=\boxed{301}.</math> | Finally, substituting this result into <math>(\bigstar)</math> gives <math>22\cos\theta=\frac{242}{59},</math> from which the answer is <math>242+59=\boxed{301}.</math> | ||
| − | ~MRENTHUSIASM | + | ~MRENTHUSIASM (credit given to Leonard my dude) |
===Remark (Ptolemy's Theorem)=== | ===Remark (Ptolemy's Theorem)=== | ||
In <math>ABCD,</math> we have | In <math>ABCD,</math> we have | ||
<cmath>\begin{align*} | <cmath>\begin{align*} | ||
| − | AE\cdot BE+BE\cdot CE+CE\cdot DE+DE\cdot AE &= (AE+CE)(BE+DE) &&\hspace{10mm}\text{Factor} \\ | + | AE\cdot BE+BE\cdot CE+CE\cdot DE+DE\cdot AE &= (AE+CE)(BE+DE) &&\hspace{10mm}\text{Factor by Grouping} \\ |
&=AC\cdot BD &&\hspace{10mm}\text{Segment Addition} \\ | &=AC\cdot BD &&\hspace{10mm}\text{Segment Addition} \\ | ||
&=AB\cdot CD+BC\cdot DA &&\hspace{10mm}\text{Ptolemy's Theorem} \\ | &=AB\cdot CD+BC\cdot DA &&\hspace{10mm}\text{Ptolemy's Theorem} \\ | ||
| − | &=59. | + | &=59. &&\hspace{10mm}\text{Substitution} |
\end{align*}</cmath> | \end{align*}</cmath> | ||
~MRENTHUSIASM | ~MRENTHUSIASM | ||
| − | ==See | + | ==Solution 2 (Finding cos x)== |
| + | The angle <math>\theta</math> between diagonals satisfies <cmath>\tan{\frac{\theta}{2}}=\sqrt{\frac{(s-b)(s-d)}{(s-a)(s-c)}}</cmath> (see https://en.wikipedia.org/wiki/Cyclic_quadrilateral#Angle_formulas). | ||
| + | Thus, <cmath>\tan{\frac{\theta}{2}}=\sqrt{\frac{(11-4)(11-6)}{(11-5)(11-7)}}\text{ or }\tan{\frac{\theta}{2}}=\sqrt{\frac{(11-5)(11-7)}{(11-4)(11-6)}}.</cmath> | ||
| + | That is, <math>\tan^2{\frac{\theta}{2}}=\frac{1-\cos^2{\frac{\theta}{2}}}{\cos^2{\frac{\theta}{2}}}=\frac{24}{35}</math> or <math>\frac{35}{24}</math>. Thus, <math>\cos^2{\frac{\theta}{2}}=\frac{35}{59}</math> or <math>\frac{24}{59}</math>. So, | ||
| + | <cmath>\cos{\theta}=2\cos^2{\frac{\theta}{2}}-1=\pm\frac{11}{59}.</cmath> | ||
| + | In this context, <math>\cos{\theta}>0</math>. Thus, <math>\cos{\theta}=\frac{11}{59}</math>. The perimeter of <math>A_1B_1C_1D_1</math> is | ||
| + | <cmath>22\cdot\cos{\theta}=22\cdot\frac{11}{59}=\frac{242}{59},</cmath> and the answer is <math>m+n=242+59=\boxed{301}</math>. | ||
| + | |||
| + | ~y.grace.yu | ||
| + | |||
| + | ==Solution 3 (Pythagorean Theorem)== | ||
| + | We assume that the two quadrilateral mentioned in the problem are similar (due to both of them being cyclic). Note that by Ptolemy’s, one of the diagonals has length <math>\sqrt{4 \cdot 6 + 5 \cdot 7} = \sqrt{59}.</math> [I don't believe this is correct... are the two diagonals of <math>ABCD</math> necessarily congruent? -peace09]* WLOG we focus on diagonal <math>BD.</math> To find the diagonal of the inner quadrilateral, we drop the altitude from <math>A</math> and <math>C</math> and calculate the length of <math>A_1C_1.</math> Let <math>x</math> be <math>A_1D</math> (Thus <math>A_1B = \sqrt{59} - x.</math> By Pythagorean theorem, we have <cmath>49 - x^2 = 16 - \left(\sqrt{59} - x\right)^2 \implies 92 = 2\sqrt{59}x \implies x = \frac{46}{\sqrt{59}} = \frac{46\sqrt{59}}{59}.</cmath> Now let <math>y</math> be <math>C_1D.</math> (thus making <math>C_1B = \sqrt{59} - y</math>). Similarly, we have <cmath>36 - y^2 = 25 - \left(\sqrt{59} - y\right)^2 \implies 70 = 2\sqrt{59}y \implies y = \frac{35}{\sqrt{59}} = \frac{35\sqrt{59}}{59}.</cmath> We see that <math>A_1C_1</math>, the scaled down diagonal is just <math>x - y = \frac{11\sqrt{59}}{59},</math> which is <math>\frac{\frac{11\sqrt{59}}{59}}{\sqrt{59}} = \frac{11}{59}</math> times our original diagonal <math>BD,</math> implying a scale factor of <math>\frac{11}{59}.</math> Thus, due to perimeters scaling linearly, the perimeter of the new quadrilateral is simply <math>\frac{11}{59} \cdot 22 = \frac{242}{59},</math> making our answer <math>242+59 = \boxed{301}.</math> | ||
| + | |||
| + | ~fidgetboss_4000 | ||
| + | |||
| + | <cmath></cmath> | ||
| + | <math>*</math>Indeed, the diagonals do not have length <math>\sqrt{59}</math>. However, here's why it works out: Let the length of diagonal BD be a. Then, by the same logic as given in the solution by fidgetboss_4000, <math>x=\frac{33+a^{2}}{2a}</math>, <math>y=\frac{11+a^{2}}{2a}</math>, so <math>x-y=\frac{11}{a}</math>. Then, why does dividing by a to get a ratio work? It's because the orientation of quadrilaterals is different! In other words, instead of diagonal BD corresponding to diagonal <math>B_1</math> <math>D_1</math>, it corresponds to diagonal <math>A_1</math> <math>C_1</math>. Thus, to get the right ratio, we can find the ratio of the multiplied diagonals, then take the square root (this square root part is crucial. It happens because we essentially are taking something two-dimensional on the numerator and denominator, so to make it a one-dimensional similarity ratio, we must take the square root to half the dimension on each part). This yields <math>\sqrt{\frac{121}{a^{2}\cdot b^{2}}}</math>=<math>\frac{11}{a\cdot b}</math>. However, by Ptolemy, <math>a\cdot b</math>=59. Thus, the ratio is indeed <math>\frac{11}{59}</math>. ~MATH-TITAN | ||
| + | |||
| + | ==Solution 4 (Symmetry)== | ||
| + | <i><b>Solution</b></i> | ||
| + | |||
| + | [[File:AIME-I-2021-11a.png|350px|right]] | ||
| + | |||
| + | In accordance with <b>Claim 1,</b> the ratios of pairs of one-color segments are the same and equal to <math>\cos \theta,</math> where <math>\theta</math> is the acute angle between the diagonals. | ||
| + | <cmath>\begin{align*} | ||
| + | s &= A'B' + B'C' + C'D' + D'A' \\ | ||
| + | &= (AB + BC + CD + DA)\cos \theta \\ | ||
| + | &= (a + b + c + d)\cos \theta \\ | ||
| + | &= 22\cos \theta. | ||
| + | \end{align*}</cmath> | ||
| + | In accordance with <b>Claim 2,</b> | ||
| + | <cmath>\begin{align*} 2(ac + bd)\cos \theta = |d^2 – c^2 + b^2 – a^2|.\end{align*}</cmath> | ||
| + | <cmath>2 \cdot 59 \cos \theta = |13 + 9|.</cmath> | ||
| + | <cmath>s = 22\cos \theta = \frac{22 \cdot 11}{59} = \frac{242}{59}.</cmath> | ||
| + | Therefore, the answer is <math>242+59=\boxed{301}.</math> | ||
| + | |||
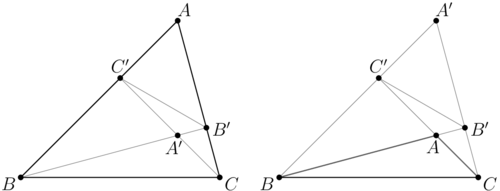
| + | <i><b>Claim 1</b></i> | ||
| + | [[File:AIME-I-2021-11b.png|500px|right]] | ||
| + | In the triangle <math>ABC</math>, the points <math>B'</math> and <math>C'</math> are the bases of the heights dropped from the vertices <math>B</math> and <math>C</math>, respectively. <math>\angle A = \alpha</math>. Then | ||
| + | <cmath>B'C'=\begin{cases} | ||
| + | BC \cos\alpha, & \textrm{if } \alpha < 90^\circ, \\ | ||
| + | BC \cos (180^\circ – \alpha), & \textrm{if } \alpha >90^\circ. | ||
| + | \end{cases}=|BC\cos{\alpha}| | ||
| + | </cmath> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Denote the orthocenter by <math>A'</math>. Quadrilateral <math>B'C'BC</math> is inscribed in a circle with diameter <math>BC</math>, so the marked <math>\angle B = \angle B'.</math> | ||
| + | |||
| + | If <math>\alpha < 90^\circ,</math> the <math>\triangle AB'C' \sim \triangle ABC,</math> the similarity coefficient is <math>AC' : AC = \cos \alpha.</math> | ||
| + | So <math>B'C' : BC = \cos \alpha.</math> | ||
| + | |||
| + | If <math>\alpha > 90^\circ,</math> the <math>\triangle A'B'C' \sim \triangle A'BC,</math> the similarity coefficient is | ||
| + | <math>A'C' : A'C = \cos (180^\circ – \alpha).</math> So <math>B'C' : BC = \cos (180^\circ – \alpha).</math> | ||
| + | |||
| + | <i><b>Claim 2</b></i> | ||
| + | [[File:AIME-I-2021-11c.png|300px|right]] | ||
| + | Given an inscribed quadrilateral <math>ABCD</math> with sides <math>AB = a, BC = b, CD = c,</math> and <math>DA = d.</math> Prove that the <math>\angle \theta < 90^\circ</math> between the diagonals is given by | ||
| + | <cmath>\begin{align*} \cos \theta = \frac {|d^2 – c^2 + b^2 – a^2|}{2(ac + bd)}.\end{align*}</cmath> | ||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Let the point <math>B'</math> be symmetric to <math>B</math> with respect to the perpendicular bisector <math>AC.</math> Then the quadrilateral <math>AB'CD</math> is an inscribed one, <math>AB' = b, B'C = a.</math> | ||
| + | |||
| + | <cmath> 2 \angle AEB = \overset{\Large\frown} {AB} + \overset{\Large\frown} {CD}.</cmath> | ||
| + | <cmath>\begin{align*} 2\angle B'AD = \overset{\Large\frown} {B'C} + \overset{\Large\frown} {CD} = \overset{\Large\frown} {AB} + \overset{\Large\frown} {CD} \implies \angle AEB = \angle B'AD\end{align*}</cmath> | ||
| + | |||
| + | We apply the Law of Cosines to <math>\triangle AB'D</math> and <math>\triangle CB'D</math>: | ||
| + | <cmath>\begin{align*} B'D^2 = AD^2 + AB'^2 – 2 AD \cdot AB' \cos \theta,\end{align*}</cmath> | ||
| + | <cmath>B'D^2 = CD^2 + CB'^2 + 2 CD \cdot CB' \cos \theta,</cmath> | ||
| + | <cmath>d^2 + b^2 – 2 bd \cos \theta = c^2 + a^2 + 2ac \cos \theta,</cmath> | ||
| + | <cmath>2(ac + bd) \cos \theta = |d^2 – c^2 + b^2 – a^2|.</cmath> | ||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Note== | ||
| + | This problem is kinda similar to [[2021 AIME II Problems/Problem 12]] | ||
| + | |||
| + | ==See Also== | ||
{{AIME box|year=2021|n=I|num-b=10|num-a=12}} | {{AIME box|year=2021|n=I|num-b=10|num-a=12}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Latest revision as of 18:56, 24 December 2023
Contents
Problem
Let ![]() be a cyclic quadrilateral with
be a cyclic quadrilateral with ![]() and
and ![]() Let
Let ![]() and
and ![]() be the feet of the perpendiculars from
be the feet of the perpendiculars from ![]() and
and ![]() respectively, to line
respectively, to line ![]() and let
and let ![]() and
and ![]() be the feet of the perpendiculars from
be the feet of the perpendiculars from ![]() and
and ![]() respectively, to line
respectively, to line ![]() The perimeter of
The perimeter of ![]() is
is ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
Diagram
![[asy] /* Made by MRENTHUSIASM */ size(300); pair A, B, C, D, A1, B1, C1, D1; A = origin; C = (sqrt(53041)/31,0); B = intersectionpoints(Circle(A,4),Circle(C,5))[0]; D = intersectionpoints(Circle(A,7),Circle(C,6))[1]; A1 = foot(A,B,D); C1 = foot(C,B,D); B1 = foot(B,A,C); D1 = foot(D,A,C); markscalefactor=0.025; draw(rightanglemark(A,A1,B),red); draw(rightanglemark(B,B1,A),red); draw(rightanglemark(C,C1,D),red); draw(rightanglemark(D,D1,C),red); draw(A1--B1--C1--D1--cycle,green); dot("$A$",A,1.5*W,linewidth(4)); dot("$B$",B,1.5*dir(180-aCos(11/59)),linewidth(4)); dot("$C$",C,1.5*E,linewidth(4)); dot("$D$",D,1.5*dir(-aCos(11/59)),linewidth(4)); dot("$A_1$",A1,1.5*dir(A1-A),linewidth(4)); dot("$B_1$",B1,1.5*S,linewidth(4)); dot("$C_1$",C1,1.5*dir(C1-C),linewidth(4)); dot("$D_1$",D1,1.5*N,linewidth(4)); draw(A--B--C--D--cycle^^A--C^^B--D^^circumcircle(A,B,C)); draw(A--A1^^B--B1^^C--C1^^D--D1,dashed); [/asy]](http://latex.artofproblemsolving.com/4/a/6/4a6f6b36da04068f790e929d7eec59aef0c1aed6.png) ~MRENTHUSIASM
~MRENTHUSIASM
Solution 1 (Cyclic Quadrilaterals, Similar Triangles, and Trigonometry)
This solution refers to the Diagram section.
By the Converse of the Inscribed Angle Theorem, if distinct points ![]() and
and ![]() lie on the same side of
lie on the same side of ![]() (but not on
(but not on ![]() itself) for which
itself) for which ![]() then
then ![]() and
and ![]() are cyclic. From the Converse of the Inscribed Angle Theorem, quadrilaterals
are cyclic. From the Converse of the Inscribed Angle Theorem, quadrilaterals ![]() and
and ![]() are all cyclic.
are all cyclic.
Suppose ![]() and
and ![]() intersect at
intersect at ![]() and let
and let ![]() It follows that
It follows that ![]() and
and ![]()
We obtain the following diagram:
![[asy] /* Made by MRENTHUSIASM */ size(300); pair A, B, C, D, A1, B1, C1, D1, P, M1, M2; A = origin; C = (sqrt(53041)/31,0); B = intersectionpoints(Circle(A,4),Circle(C,5))[0]; D = intersectionpoints(Circle(A,7),Circle(C,6))[1]; A1 = foot(A,B,D); C1 = foot(C,B,D); B1 = foot(B,A,C); D1 = foot(D,A,C); P = intersectionpoint(A--C,B--D); M1 = midpoint(A--B); M2 = midpoint(C--D); markscalefactor=0.025; draw(rightanglemark(A,A1,B),red); draw(rightanglemark(B,B1,A),red); draw(rightanglemark(C,C1,D),red); draw(rightanglemark(D,D1,C),red); draw(Arc(M1,A,B)^^Arc(M2,C,D),blue); draw(A1--B1--C1--D1--cycle,green); dot("$A$",A,1.5*W,linewidth(4)); dot("$B$",B,1.5*dir(180-aCos(11/59)),linewidth(4)); dot("$C$",C,1.5*E,linewidth(4)); dot("$D$",D,1.5*dir(-aCos(11/59)),linewidth(4)); dot("$A_1$",A1,1.5*dir(A1-A),linewidth(4)); dot("$B_1$",B1,1.5*S,linewidth(4)); dot("$C_1$",C1,1.5*dir(C1-C),linewidth(4)); dot("$D_1$",D1,1.5*N,linewidth(4)); dot("$E$",P,dir((180-aCos(11/59))/2),linewidth(4)); label("$\theta$",P,dir(180-aCos(11/59)/2),red); draw(A--B--C--D--cycle^^A--C^^B--D^^circumcircle(A,B,C)); draw(A--A1^^B--B1^^C--C1^^D--D1,dashed); [/asy]](http://latex.artofproblemsolving.com/1/7/6/176d8f879cf739392be8f3a10297d15ed548db67.png) In every cyclic quadrilateral, each pair of opposite angles is supplementary. So, we have
In every cyclic quadrilateral, each pair of opposite angles is supplementary. So, we have ![]() (both supplementary to
(both supplementary to ![]() ) and
) and ![]() (both supplementary to
(both supplementary to ![]() ), from which
), from which ![]() by AA, with the ratio of similitude
by AA, with the ratio of similitude ![\[\frac{A_1B_1}{AB}=\underbrace{\frac{A_1E}{AE}}_{\substack{\text{right} \\ \triangle A_1AE}}=\underbrace{\frac{B_1E}{BE}}_{\substack{\text{right} \\ \triangle B_1BE}}=\cos\theta. \hspace{15mm}(1)\]](http://latex.artofproblemsolving.com/d/4/d/d4db43e8608477497fbb257d17bfe041000b4d5f.png) Similarly, we have
Similarly, we have ![]() (both supplementary to
(both supplementary to ![]() ) and
) and ![]() (both supplementary to
(both supplementary to ![]() ), from which
), from which ![]() by AA, with the ratio of similitude
by AA, with the ratio of similitude ![\[\frac{C_1D_1}{CD}=\underbrace{\frac{C_1E}{CE}}_{\substack{\text{right} \\ \triangle C_1CE}}=\underbrace{\frac{D_1E}{DE}}_{\substack{\text{right} \\ \triangle D_1DE}}=\cos\theta. \hspace{14.75mm}(2)\]](http://latex.artofproblemsolving.com/6/2/f/62f9cf8e1812c9bd4aaec0b5a8408cea5a37f597.png) We apply the Transitive Property to
We apply the Transitive Property to ![]() and
and ![]()
- We get
 so
so  by SAS, with the ratio of similitude
by SAS, with the ratio of similitude ![\[\frac{B_1C_1}{BC}=\frac{B_1E}{BE}=\frac{C_1E}{CE}=\cos\theta. \hspace{14.75mm}(3)\]](//latex.artofproblemsolving.com/3/2/1/32130f85d69205e70793791c48e5faefed46e1fd.png)
- We get
 so
so  by SAS, with the ratio of similitude
by SAS, with the ratio of similitude ![\[\frac{D_1A_1}{DA}=\frac{D_1E}{DE}=\frac{A_1E}{AE}=\cos\theta. \hspace{14mm}(4)\]](//latex.artofproblemsolving.com/1/1/5/115bc444769d7d350cdfbdf6c13c34ddfd82fa06.png)
From ![]() and
and ![]() the perimeter of
the perimeter of ![]() is
is
 Two solutions follow from here:
Two solutions follow from here:
Solution 1.1 (Law of Cosines)
Note that ![]() holds for all
holds for all ![]() We apply the Law of Cosines to
We apply the Law of Cosines to ![]() and
and ![]() respectively:
respectively:
 We subtract
We subtract ![]() from
from ![]()
 Finally, substituting this result into
Finally, substituting this result into ![]() gives
gives ![]() from which the answer is
from which the answer is ![]()
~MRENTHUSIASM (credit given to Math Jams's 2021 AIME I Discussion)
Solution 1.2 (Area Formulas)
Let the brackets denote areas.
We find ![]() in two different ways:
in two different ways:
- Note that
 holds for all
holds for all  By area addition, we get
By area addition, we get
![\begin{align*} [ABCD]&=[ABE]+[BCE]+[CDE]+[DAE] \\ &=\frac12\cdot AE\cdot BE\cdot\sin\angle AEB+\frac12\cdot BE\cdot CE\cdot\sin\angle BEC+\frac12\cdot CE\cdot DE\cdot\sin\angle CED+\frac12\cdot DE\cdot AE\cdot\sin\angle DEA \\ &=\frac12\cdot AE\cdot BE\cdot\sin\theta+\frac12\cdot BE\cdot CE\cdot\sin\theta+\frac12\cdot CE\cdot DE\cdot\sin\theta+\frac12\cdot DE\cdot AE\cdot\sin\theta \\ &=\frac12\cdot\sin\theta\cdot(\phantom{ }\underbrace{AE\cdot BE+BE\cdot CE+CE\cdot DE+DE\cdot AE}_{\text{Use the result from }\textbf{Remark}\text{.}}\phantom{ }) \\ &=\frac12\cdot\sin\theta\cdot59. \end{align*}](//latex.artofproblemsolving.com/7/0/1/70179c9e0e55870390f958d93238725d162e28c2.png)
- By Brahmagupta's Formula, we get
![\[[ABCD]=\sqrt{(s-AB)(s-BC)(s-CD)(s-DA)}=2\sqrt{210},\]](//latex.artofproblemsolving.com/f/f/6/ff61697de589a72c67a713bf5e8349af8fe727f0.png) where
where  is the semiperimeter of
is the semiperimeter of 
Equating the expressions for ![]() we have
we have
![]() so
so ![]() Since
Since ![]() we have
we have ![]() It follows that
It follows that ![]() Finally, substituting this result into
Finally, substituting this result into ![]() gives
gives ![]() from which the answer is
from which the answer is ![]()
~MRENTHUSIASM (credit given to Leonard my dude)
Remark (Ptolemy's Theorem)
In ![]() we have
we have
 ~MRENTHUSIASM
~MRENTHUSIASM
Solution 2 (Finding cos x)
The angle ![]() between diagonals satisfies
between diagonals satisfies ![\[\tan{\frac{\theta}{2}}=\sqrt{\frac{(s-b)(s-d)}{(s-a)(s-c)}}\]](http://latex.artofproblemsolving.com/9/7/c/97c3d3b8825eea07df794427667b774cbf27b7c8.png) (see https://en.wikipedia.org/wiki/Cyclic_quadrilateral#Angle_formulas).
Thus,
(see https://en.wikipedia.org/wiki/Cyclic_quadrilateral#Angle_formulas).
Thus, ![\[\tan{\frac{\theta}{2}}=\sqrt{\frac{(11-4)(11-6)}{(11-5)(11-7)}}\text{ or }\tan{\frac{\theta}{2}}=\sqrt{\frac{(11-5)(11-7)}{(11-4)(11-6)}}.\]](http://latex.artofproblemsolving.com/b/b/1/bb12544c5cf0ec157efef2cc3658d8a52bf82e8e.png) That is,
That is, ![]() or
or ![]() . Thus,
. Thus, ![]() or
or ![]() . So,
. So,
![]() In this context,
In this context, ![]() . Thus,
. Thus, ![]() . The perimeter of
. The perimeter of ![]() is
is
![]() and the answer is
and the answer is ![]() .
.
~y.grace.yu
Solution 3 (Pythagorean Theorem)
We assume that the two quadrilateral mentioned in the problem are similar (due to both of them being cyclic). Note that by Ptolemy’s, one of the diagonals has length ![]() [I don't believe this is correct... are the two diagonals of
[I don't believe this is correct... are the two diagonals of ![]() necessarily congruent? -peace09]* WLOG we focus on diagonal
necessarily congruent? -peace09]* WLOG we focus on diagonal ![]() To find the diagonal of the inner quadrilateral, we drop the altitude from
To find the diagonal of the inner quadrilateral, we drop the altitude from ![]() and
and ![]() and calculate the length of
and calculate the length of ![]() Let
Let ![]() be
be ![]() (Thus
(Thus ![]() By Pythagorean theorem, we have
By Pythagorean theorem, we have ![]() Now let
Now let ![]() be
be ![]() (thus making
(thus making ![]() ). Similarly, we have
). Similarly, we have ![]() We see that
We see that ![]() , the scaled down diagonal is just
, the scaled down diagonal is just ![]() which is
which is ![]() times our original diagonal
times our original diagonal ![]() implying a scale factor of
implying a scale factor of ![]() Thus, due to perimeters scaling linearly, the perimeter of the new quadrilateral is simply
Thus, due to perimeters scaling linearly, the perimeter of the new quadrilateral is simply ![]() making our answer
making our answer ![]()
~fidgetboss_4000
![\[\]](http://latex.artofproblemsolving.com/5/7/f/57f1406b65f9f2e6a365b7356da731780b42cceb.png)
![]() Indeed, the diagonals do not have length
Indeed, the diagonals do not have length ![]() . However, here's why it works out: Let the length of diagonal BD be a. Then, by the same logic as given in the solution by fidgetboss_4000,
. However, here's why it works out: Let the length of diagonal BD be a. Then, by the same logic as given in the solution by fidgetboss_4000, ![]() ,
, ![]() , so
, so ![]() . Then, why does dividing by a to get a ratio work? It's because the orientation of quadrilaterals is different! In other words, instead of diagonal BD corresponding to diagonal
. Then, why does dividing by a to get a ratio work? It's because the orientation of quadrilaterals is different! In other words, instead of diagonal BD corresponding to diagonal ![]()
![]() , it corresponds to diagonal
, it corresponds to diagonal ![]()
![]() . Thus, to get the right ratio, we can find the ratio of the multiplied diagonals, then take the square root (this square root part is crucial. It happens because we essentially are taking something two-dimensional on the numerator and denominator, so to make it a one-dimensional similarity ratio, we must take the square root to half the dimension on each part). This yields
. Thus, to get the right ratio, we can find the ratio of the multiplied diagonals, then take the square root (this square root part is crucial. It happens because we essentially are taking something two-dimensional on the numerator and denominator, so to make it a one-dimensional similarity ratio, we must take the square root to half the dimension on each part). This yields ![]() =
=![]() . However, by Ptolemy,
. However, by Ptolemy, ![]() =59. Thus, the ratio is indeed
=59. Thus, the ratio is indeed ![]() . ~MATH-TITAN
. ~MATH-TITAN
Solution 4 (Symmetry)
Solution
In accordance with Claim 1, the ratios of pairs of one-color segments are the same and equal to ![]() where
where ![]() is the acute angle between the diagonals.
is the acute angle between the diagonals.
 In accordance with Claim 2,
In accordance with Claim 2,
![]()
![]()
![]() Therefore, the answer is
Therefore, the answer is ![]()
Claim 1
In the triangle ![]() , the points
, the points ![]() and
and ![]() are the bases of the heights dropped from the vertices
are the bases of the heights dropped from the vertices ![]() and
and ![]() , respectively.
, respectively. ![]() . Then
. Then
![\[B'C'=\begin{cases} BC \cos\alpha, & \textrm{if } \alpha < 90^\circ, \\ BC \cos (180^\circ – \alpha), & \textrm{if } \alpha >90^\circ. \end{cases}=|BC\cos{\alpha}|\]](http://latex.artofproblemsolving.com/7/7/9/77944a5070a6111bd4c3f6858a4bbc0c502ef2f6.png)
Proof
Denote the orthocenter by ![]() . Quadrilateral
. Quadrilateral ![]() is inscribed in a circle with diameter
is inscribed in a circle with diameter ![]() , so the marked
, so the marked ![]()
If ![]() the
the ![]() the similarity coefficient is
the similarity coefficient is ![]() So
So ![]()
If ![]() the
the ![]() the similarity coefficient is
the similarity coefficient is
![]() So
So ![]()
Claim 2
Given an inscribed quadrilateral ![]() with sides
with sides ![]() and
and ![]() Prove that the
Prove that the ![]() between the diagonals is given by
between the diagonals is given by
![]() Proof
Proof
Let the point ![]() be symmetric to
be symmetric to ![]() with respect to the perpendicular bisector
with respect to the perpendicular bisector ![]() Then the quadrilateral
Then the quadrilateral ![]() is an inscribed one,
is an inscribed one, ![]()
![]()
![]()
We apply the Law of Cosines to ![]() and
and ![]() :
:
![]()
![]()
![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Note
This problem is kinda similar to 2021 AIME II Problems/Problem 12
See Also
| 2021 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 10 |
Followed by Problem 12 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 





![\begin{align*} [ABCD]&=[ABE]+[BCE]+[CDE]+[DAE] \\ &=\frac12\cdot AE\cdot BE\cdot\sin\angle AEB+\frac12\cdot BE\cdot CE\cdot\sin\angle BEC+\frac12\cdot CE\cdot DE\cdot\sin\angle CED+\frac12\cdot DE\cdot AE\cdot\sin\angle DEA \\ &=\frac12\cdot AE\cdot BE\cdot\sin\theta+\frac12\cdot BE\cdot CE\cdot\sin\theta+\frac12\cdot CE\cdot DE\cdot\sin\theta+\frac12\cdot DE\cdot AE\cdot\sin\theta \\ &=\frac12\cdot\sin\theta\cdot(\phantom{ }\underbrace{AE\cdot BE+BE\cdot CE+CE\cdot DE+DE\cdot AE}_{\text{Use the result from }\textbf{Remark}\text{.}}\phantom{ }) \\ &=\frac12\cdot\sin\theta\cdot59. \end{align*}](http://latex.artofproblemsolving.com/7/0/1/70179c9e0e55870390f958d93238725d162e28c2.png)