Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Orthic triangle"
m (→‎Incenter of the orthic triangle)
 
(15 intermediate revisions by 3 users not shown)
Line 3: Line 3:
 
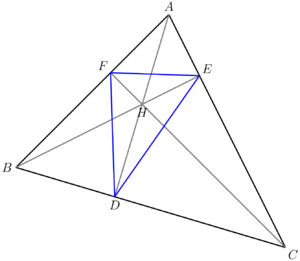
In [[geometry]], given any <math>\triangle ABC</math>, let <math>D</math>, <math>E</math>, and <math>F</math> denote the feet of the altitudes from <math>A</math>, <math>B</math>, and <math>C</math>, respectively. Then, <math>\triangle DEF</math> is called the '''orthic triangle''' of <math>\triangle ABC</math>.
 
In [[geometry]], given any <math>\triangle ABC</math>, let <math>D</math>, <math>E</math>, and <math>F</math> denote the feet of the altitudes from <math>A</math>, <math>B</math>, and <math>C</math>, respectively. Then, <math>\triangle DEF</math> is called the '''orthic triangle''' of <math>\triangle ABC</math>.
  
−
It's easy to see that there is no orthic triangle if <math>\triangle ABC</math> is right. The two cases are when <math>\triangle ABC</math> is either acute or obtuse must be handled separately, as they each carry different characteristics.
+
The orthic triangle does not exist if <math>\triangle ABC</math> is right. The two cases of when <math>\triangle ABC</math> is either acute or obtuse each carry different characteristics and must be handled separately.
  
−
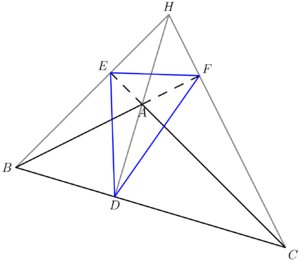
Orthic triangles are not unique to their mother triangles, as one acute and one to three obtuse triangles are guaranteed to have the same orthic triangle. To see this, take an acute triangle and swap its orthocenter and any vertex to get an obtuse triangle. It's easy to verify that this placement of the orthocenter is correct and that the orthic triangle will remain the same as before the swapping, as seen in the diagrams to the right.
+
Orthic triangles are not unique to their mother triangle; one acute and one to three obtuse triangles are guaranteed to have the same orthic triangle. To see this, take an acute triangle and swap its orthocenter and any vertex to get an obtuse triangle. It is easy to verify that this placement of the orthocenter is correct and that the orthic triangle will remain the same as before the swapping, as seen in the diagrams to the right.
  
 
== Cyclic quadrilaterals ==
 
== Cyclic quadrilaterals ==
−
In both the acute and obtuse case, quadrilaterals <math>ADEB</math>, <math>BEFC</math>, <math>CFDA</math>, <math>AEHF</math>, <math>BFHD</math>, and <math>CDHE</math> are [[Cyclic quadrilateral | cyclic]].
+
In both the acute and obtuse case, quadrilaterals <math>ADEB</math>, <math>BEFC</math>, <math>CFAD</math>, <math>AEHF</math>, <math>BFHD</math>, and <math>CDHE</math> are [[Cyclic quadrilateral | cyclic]]. These cyclic quadrilaterals make frequent appearances in olympiad geometry and are the most crucial section of this article.
  
−
''Proof'': we will be using [[directed angles]], denoted by <math>\measuredangle</math> instead of the conventional <math>\angle</math>. We know that <cmath>\measuredangle ADB = 90^{\circ} = \measuredangle AEB,</cmath> and thus <math>ADEB</math> is cyclic. In addition, <cmath>\measuredangle AEH = 90^{\circ} = \measuredangle AFH,</cmath> so <math>AEHF</math> is also cyclic. It follows that the other cyclic quadrilaterals are also cyclic. <math>\square</math>
+
''Proof'': we will be using [[directed angles]], denoted by <math>\measuredangle</math> instead of the conventional <math>\angle</math>. We know that <cmath>\measuredangle ADB = 90^{\circ} = \measuredangle AEB,</cmath> and thus <math>AEDB</math> is cyclic. In addition, <cmath>\measuredangle AEH = 90^{\circ} = \measuredangle AFH,</cmath> so <math>AEHF</math> is also cyclic. It follows that the other cyclic quadrilaterals are also cyclic.
−
 
+
<math>\square</math>
−
These cyclic quadrilaterals make frequent appearances in olympiad geometry and are the most crucial section of this article.
 
  
 
== Connection with incenters and excenters ==
 
== Connection with incenters and excenters ==
Line 19: Line 18:
 
If <math>\triangle ABC</math> is acute, then the incenter of the orthic triangle of <math>\triangle ABC</math> is the orthocenter <math>H</math>.
 
If <math>\triangle ABC</math> is acute, then the incenter of the orthic triangle of <math>\triangle ABC</math> is the orthocenter <math>H</math>.
  
−
''Proof'':  
+
''Proof'': Let <math>\theta = \angle EAH</math>. Since <math>\angle ADC = 90^\circ</math>, we have that <math>\theta = 90^\circ - \angle C</math>. The quadrilateral <math>EAFH</math> is cyclic and, in fact <math>E</math> and <math>F</math> lie on the circle with diameter <math>AH</math>. Since <math>EH</math> subtends <math>\theta</math> as well as <math>\angle EFH</math> on this circle, so <math>\angle EFH = \theta = 90^\circ - \angle C</math>. The same argument (with <math>FBDH</math> instead of <math>EAFH</math>) shows that <math>\angle DFH = 90^\circ - \angle C</math>. Hence <math>\angle EFH = \angle DFH</math>, i.e. the line <math>HF</math> bisects <math>\angle EFD</math>. By the same reasoning <math>HD</math> bisects <math>\angle EDF</math> and <math>HE</math> bisects <math>\angle FED</math>.
 +
<math>\square</math>
  
 
If <math>\triangle ABC</math> is obtuse, then the incenter of the orthic triangle of <math>\triangle ABC</math> is the obtuse vertex.
 
If <math>\triangle ABC</math> is obtuse, then the incenter of the orthic triangle of <math>\triangle ABC</math> is the obtuse vertex.
Line 28: Line 28:
 
''Proof'': First, we show that the orthic triangle leads to the excenters. Let <math>D</math>, <math>E</math>, and <math>F</math> be on <math>\overline{AB}</math>, <math>\overline{BC}</math>, and <math>\overline{CA}</math>, respectively. Because <math>ADEB</math> is cyclic, <math>\angle EDC = \angle A</math>. Likewise, <math>\angle BDF = \angle A</math> as well. Then because <math>\angle BDF + \angle D + \angle EDC = 180^{\circ}</math>, <math>\angle A + \angle D + \angle A = 180^{\circ}</math> and so <math>\angle D = 180^{\circ} - 2\angle A</math>.
 
''Proof'': First, we show that the orthic triangle leads to the excenters. Let <math>D</math>, <math>E</math>, and <math>F</math> be on <math>\overline{AB}</math>, <math>\overline{BC}</math>, and <math>\overline{CA}</math>, respectively. Because <math>ADEB</math> is cyclic, <math>\angle EDC = \angle A</math>. Likewise, <math>\angle BDF = \angle A</math> as well. Then because <math>\angle BDF + \angle D + \angle EDC = 180^{\circ}</math>, <math>\angle A + \angle D + \angle A = 180^{\circ}</math> and so <math>\angle D = 180^{\circ} - 2\angle A</math>.
  
−
Thus, the exterior angle of <math>\angle D</math> is <math>2\angle A</math>. But <math>\angle BDF = \angle EDC = \angle A</math>, so <math>\overline{BC}</math> bisects the exterior angle of <math>\angle D</math>. Similarly, <math>\overline{CA}</math> and <math>\overline{AB}</math> bisect the exterior angles of <math>\angle E</math> and <math>\angle F</math> respectively. Thus, the intersections of <math>\overline{AB}</math>, <math>\overline{BC}</math>, and <math>\overline{CA}</math> (namely <math>A</math>, <math>B</math>, and <math>C</math>) are the excenters of <math>\triangle DEF</math>, and we're done.
+
Thus, the exterior angle of <math>\angle D</math> is <math>2\angle A</math>. But <math>\angle BDF = \angle EDC = \angle A</math>, so <math>\overline{BC}</math> bisects the exterior angle of <math>\angle D</math>. Similarly, <math>\overline{CA}</math> and <math>\overline{AB}</math> bisect the exterior angles of <math>\angle E</math> and <math>\angle F</math> respectively. Thus, the intersections of <math>\overline{AB}</math>, <math>\overline{BC}</math>, and <math>\overline{CA}</math> (namely <math>A</math>, <math>B</math>, and <math>C</math>) are the excenters of <math>\triangle DEF</math>, and we are halfway finished.  
  
−
Next, we show that the excenters lead to the orthic triangle. Let <math>A</math>, <math>B</math>, and <math>C</math> be the <math>D</math>-excenter, <math>E</math>-excenter, and <math>F</math>-excenter of <math>\triangle DEF</math>, and let <math>H</math> be the incenter of <math>\triangle DEF</math>. <math>A</math> is equidistant from <math>\overline{DE}</math> and <math>\overline{FE}</math>, so <math>A</math> is on <math>\overline{DH}</math>, and <math>\overline{AH}</math> is an internal angle bisector of <math>\angle D</math>.  
+
Next, we show that the excenters lead to the orthic triangle. Let <math>A</math>, <math>B</math>, and <math>C</math> be the <math>D</math>-excenter, <math>E</math>-excenter, and <math>F</math>-excenter of <math>\triangle DEF</math>, and let <math>H</math> be the incenter of <math>\triangle DEF</math>. <math>A</math> is equidistant from <math>\overline{DE}</math> and <math>\overline{FE}</math>, so <math>A</math> is on <math>\overline{DH}</math>; as a result, <math>\overline{AH}</math> is an internal angle bisector of <math>\angle D</math>.  
  
−
We know that <math>\angle ADE = \frac{1}{2} \angle D</math> and because <math>C</math> is an <math>F</math>-excenter of <math>\triangle DEF</math>, <math>\angle EDC = 90^{\circ} - \frac{1}{2} \angle D</math>. Thus, <math>\angle ADC = 90^{\circ}</math>, and because <math>D</math> is on <math>\overline{BC}</math>, <math>D</math> is the foot of the altitude from <math>A</math> of <math>\triangle ABC</math>. Similarly, <math>E</math> and <math>F</math> are feet of the altitudes from <math>B</math> and <math>C</math>, respectively. Then <math>\triangle DEF</math> is the orthic triangle of <math>\triangle ABC</math>, and we are done. <math>\square</math>
+
We know that <math>\angle ADE = \frac{1}{2} \angle D</math> and because <math>C</math> is an <math>F</math>-excenter of <math>\triangle DEF</math>, <math>\angle EDC = 90^{\circ} - \frac{1}{2} \angle D</math>. Thus, <math>\angle ADC = 90^{\circ}</math>, and because <math>D</math> is on <math>\overline{BC}</math>, <math>D</math> is the foot of the altitude from <math>A</math> of <math>\triangle ABC</math>. Similarly, <math>E</math> and <math>F</math> are feet of the altitudes from <math>B</math> and <math>C</math>, respectively. Then <math>\triangle DEF</math> is the orthic triangle of <math>\triangle ABC</math>, and we are done.
 +
<math>\square</math>
 +
 
 +
This lemma makes frequent appearances in olympiad geometry. Problems written in either excenters or the orthic triangle can often be solved by shifting perspective to the other, via the medium of this lemma. Also, note the converse works as well.
  
 
In the obtuse case, the two vertices with acute angles and the [[orthocenter]] of <math>\triangle ABC</math> are the excenters.
 
In the obtuse case, the two vertices with acute angles and the [[orthocenter]] of <math>\triangle ABC</math> are the excenters.
Line 46: Line 49:
  
 
== Problems ==
 
== Problems ==
 +
* In acute triangle <math>ABC</math> points <math>P</math> and <math>Q</math> are the feet of the perpendiculars from <math>C</math> to <math>\overline{AB}</math> and from <math>B</math> to <math>\overline{AC}</math>, respectively. Line <math>PQ</math> intersects the circumcircle of <math>\triangle ABC</math> in two distinct points, <math>X</math> and <math>Y</math>. Suppose <math>XP=10</math>, <math>PQ=25</math>, and <math>QY=15</math>. Compute the product <math>AB\cdot AC</math>.  (AIME II, 2019, 15)
 
===Olympiad===
 
===Olympiad===
 
* Let <math>\triangle ABC</math> be an acute triangle with <math>D</math>, <math>E</math>, <math>F</math> the feet of the altitudes lying on <math>\overline{BC}</math>, <math>\overline{CA}</math>, and <math>\overline{AB}</math> respectively. One of the intersection points of the line <math>\overline{EF}</math> and the circumcircle is <math>P</math>. The lines <math>\overline{BP}</math> and <math>\overline{DF}</math> meet at point <math>Q</math>. Prove that <math>|AP| = |AQ|</math>. (IMO Shortlist 2010 G1)
 
* Let <math>\triangle ABC</math> be an acute triangle with <math>D</math>, <math>E</math>, <math>F</math> the feet of the altitudes lying on <math>\overline{BC}</math>, <math>\overline{CA}</math>, and <math>\overline{AB}</math> respectively. One of the intersection points of the line <math>\overline{EF}</math> and the circumcircle is <math>P</math>. The lines <math>\overline{BP}</math> and <math>\overline{DF}</math> meet at point <math>Q</math>. Prove that <math>|AP| = |AQ|</math>. (IMO Shortlist 2010 G1)
  
 
== See also ==
 
== See also ==
−
* [[Incenter/excenter lemma]]
+
* [[Incenter/excenter lemma]]
 +
* [[Geometry/Olympiad | Olympiad geometry]]
  
 
[[Category:Geometry]]
 
[[Category:Geometry]]
−
 
 
[[Category:Definition]]
 
[[Category:Definition]]

Latest revision as of 08:39, 10 July 2024

Case 1: $\triangle ABC$ is acute.
Case 2: $\triangle ABC$ is obtuse.

In geometry, given any $\triangle ABC$, let $D$, $E$, and $F$ denote the feet of the altitudes from $A$, $B$, and $C$, respectively. Then, $\triangle DEF$ is called the orthic triangle of $\triangle ABC$.

The orthic triangle does not exist if $\triangle ABC$ is right. The two cases of when $\triangle ABC$ is either acute or obtuse each carry different characteristics and must be handled separately.

Orthic triangles are not unique to their mother triangle; one acute and one to three obtuse triangles are guaranteed to have the same orthic triangle. To see this, take an acute triangle and swap its orthocenter and any vertex to get an obtuse triangle. It is easy to verify that this placement of the orthocenter is correct and that the orthic triangle will remain the same as before the swapping, as seen in the diagrams to the right.

Cyclic quadrilaterals

In both the acute and obtuse case, quadrilaterals $ADEB$, $BEFC$, $CFAD$, $AEHF$, $BFHD$, and $CDHE$ are cyclic. These cyclic quadrilaterals make frequent appearances in olympiad geometry and are the most crucial section of this article.

Proof: we will be using directed angles, denoted by $\measuredangle$ instead of the conventional $\angle$. We know that \[\measuredangle ADB = 90^{\circ} = \measuredangle AEB,\] and thus $AEDB$ is cyclic. In addition, \[\measuredangle AEH = 90^{\circ} = \measuredangle AFH,\] so $AEHF$ is also cyclic. It follows that the other cyclic quadrilaterals are also cyclic. $\square$

Connection with incenters and excenters

Incenter of the orthic triangle

If $\triangle ABC$ is acute, then the incenter of the orthic triangle of $\triangle ABC$ is the orthocenter $H$.

Proof: Let $\theta = \angle EAH$. Since $\angle ADC = 90^\circ$, we have that $\theta = 90^\circ - \angle C$. The quadrilateral $EAFH$ is cyclic and, in fact $E$ and $F$ lie on the circle with diameter $AH$. Since $EH$ subtends $\theta$ as well as $\angle EFH$ on this circle, so $\angle EFH = \theta = 90^\circ - \angle C$. The same argument (with $FBDH$ instead of $EAFH$) shows that $\angle DFH = 90^\circ - \angle C$. Hence $\angle EFH = \angle DFH$, i.e. the line $HF$ bisects $\angle EFD$. By the same reasoning $HD$ bisects $\angle EDF$ and $HE$ bisects $\angle FED$. $\square$

If $\triangle ABC$ is obtuse, then the incenter of the orthic triangle of $\triangle ABC$ is the obtuse vertex.

Excenters of the orthic triangle

For any acute $\triangle ABC$ and any $\triangle DEF$, $\triangle DEF$ is the orthic triangle of $\triangle ABC$ if and only if $A$, $B$, and $C$ are the excenters of $\triangle DEF$.

Proof: First, we show that the orthic triangle leads to the excenters. Let $D$, $E$, and $F$ be on $\overline{AB}$, $\overline{BC}$, and $\overline{CA}$, respectively. Because $ADEB$ is cyclic, $\angle EDC = \angle A$. Likewise, $\angle BDF = \angle A$ as well. Then because $\angle BDF + \angle D + \angle EDC = 180^{\circ}$, $\angle A + \angle D + \angle A = 180^{\circ}$ and so $\angle D = 180^{\circ} - 2\angle A$.

Thus, the exterior angle of $\angle D$ is $2\angle A$. But $\angle BDF = \angle EDC = \angle A$, so $\overline{BC}$ bisects the exterior angle of $\angle D$. Similarly, $\overline{CA}$ and $\overline{AB}$ bisect the exterior angles of $\angle E$ and $\angle F$ respectively. Thus, the intersections of $\overline{AB}$, $\overline{BC}$, and $\overline{CA}$ (namely $A$, $B$, and $C$) are the excenters of $\triangle DEF$, and we are halfway finished.

Next, we show that the excenters lead to the orthic triangle. Let $A$, $B$, and $C$ be the $D$-excenter, $E$-excenter, and $F$-excenter of $\triangle DEF$, and let $H$ be the incenter of $\triangle DEF$. $A$ is equidistant from $\overline{DE}$ and $\overline{FE}$, so $A$ is on $\overline{DH}$; as a result, $\overline{AH}$ is an internal angle bisector of $\angle D$.

We know that $\angle ADE = \frac{1}{2} \angle D$ and because $C$ is an $F$-excenter of $\triangle DEF$, $\angle EDC = 90^{\circ} - \frac{1}{2} \angle D$. Thus, $\angle ADC = 90^{\circ}$, and because $D$ is on $\overline{BC}$, $D$ is the foot of the altitude from $A$ of $\triangle ABC$. Similarly, $E$ and $F$ are feet of the altitudes from $B$ and $C$, respectively. Then $\triangle DEF$ is the orthic triangle of $\triangle ABC$, and we are done. $\square$

This lemma makes frequent appearances in olympiad geometry. Problems written in either excenters or the orthic triangle can often be solved by shifting perspective to the other, via the medium of this lemma. Also, note the converse works as well.

In the obtuse case, the two vertices with acute angles and the orthocenter of $\triangle ABC$ are the excenters.

Relationship with the incenter/excenter lemma

With this knowledge in mind, we can transfer results about the incenter and excenters to the orthic triangle. In particular, the incenter/excenter lemma can be translated into the language of the orthic triangle. It tells that all six cyclic quadrilaterals of the orthic triangle have a circumcenter on the nine-point circle of $\triangle ABC$.

In the case where $\triangle ABC$ is acute, quadrilaterals $AEHF$, $BFHD$, and $CDHE$ follow immediately from the lemma. Actually, because $\angle AEH = 90^{\circ}$, the circumcenter of $AEHF$ is the midpoint of $A$ and $H$, called an Euler point. It follows that the circumcenters of $BFHD$ and $CDHE$ are the other two Euler points.

As for $ADEB$, $BEFC$, and $CFDA$, via the inscribed angle theorem, their circumcenters are the midpoints of the side lengths of $\triangle ABC$, which we know to be on the nine-point circle.

Identical reasoning follows that in the obtuse case, the six cyclic quadrilaterals still have circumcenters on the nine-point circle.

Problems

  • In acute triangle $ABC$ points $P$ and $Q$ are the feet of the perpendiculars from $C$ to $\overline{AB}$ and from $B$ to $\overline{AC}$, respectively. Line $PQ$ intersects the circumcircle of $\triangle ABC$ in two distinct points, $X$ and $Y$. Suppose $XP=10$, $PQ=25$, and $QY=15$. Compute the product $AB\cdot AC$. (AIME II, 2019, 15)

Olympiad

  • Let $\triangle ABC$ be an acute triangle with $D$, $E$, $F$ the feet of the altitudes lying on $\overline{BC}$, $\overline{CA}$, and $\overline{AB}$ respectively. One of the intersection points of the line $\overline{EF}$ and the circumcircle is $P$. The lines $\overline{BP}$ and $\overline{DF}$ meet at point $Q$. Prove that $|AP| = |AQ|$. (IMO Shortlist 2010 G1)

See also

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Orthic_triangle&oldid=222001"