Difference between revisions of "2007 AMC 12B Problems/Problem 6"
(→Solution) |
|||
| (5 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | ==Problem== | |
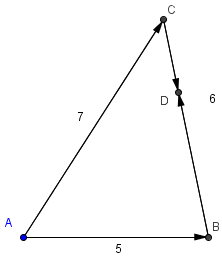
| − | A | + | Triangle <math>ABC</math> has side lengths <math>AB = 5</math>, <math>BC = 6</math>, and <math>AC = 7</math>. Two bugs start simultaneously from <math>A</math> and crawl along the sides of the triangle in opposite directions at the same speed. They meet at point <math>D</math>. What is <math>BD</math>? |
| + | <math>\mathrm {(A)}\ 1 \qquad \mathrm {(B)}\ 2 \qquad \mathrm {(C)}\ 3 \qquad \mathrm {(D)}\ 4 \qquad \mathrm {(E)}\ 5</math> | ||
| − | {{ | + | ==Solution== |
| − | {{ | + | [[Image:2007_12B_AMC-6.png]] |
| + | |||
| + | One bug goes to <math>B</math>. The path that he takes is <math>\dfrac{5+6+7}{2}=9</math> units long. The length of <math>BD</math> is <math>9-AB=9-5=4 \Rightarrow \mathrm {(D)}</math> | ||
| + | |||
| + | ==See also== | ||
| + | {{AMC12 box|year=2007|ab=B|num-b=5|num-a=7}} | ||
| + | |||
| + | [[Category:Introductory Geometry Problems]] | ||
| + | {{MAA Notice}} | ||
Latest revision as of 03:21, 15 December 2020
Problem
Triangle 
has side lengths 
, 
, and 
. Two bugs start simultaneously from 
and crawl along the sides of the triangle in opposite directions at the same speed. They meet at point 
. What is 
?
Solution
One bug goes to 
. The path that he takes is 
units long. The length of is 
See also
| 2007 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 5 |
Followed by Problem 7 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 
