Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2021 April MIMC 10 Problems/Problem 22"

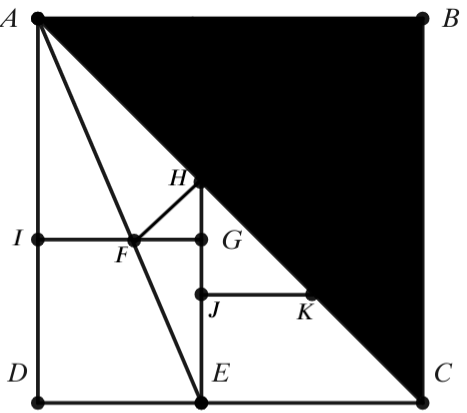
(Created page with "In the diagram, <math>ABCD</math> is a square with area <math>6+4\sqrt{2}</math>. <math>AC</math> is a diagonal of square <math>ABCD</math>. Square <math>IGED</math> has area...")
 
(→‎Solution)
 
(2 intermediate revisions by the same user not shown)
Line 5: Line 5:
 
<math>\textbf{(A)} ~5 \qquad\textbf{(B)} ~15 \qquad\textbf{(C)} ~61 \qquad\textbf{(D)} ~349 \qquad\textbf{(E)} ~2009 \qquad</math>
 
<math>\textbf{(A)} ~5 \qquad\textbf{(B)} ~15 \qquad\textbf{(C)} ~61 \qquad\textbf{(D)} ~349 \qquad\textbf{(E)} ~2009 \qquad</math>
 
==Solution==
 
==Solution==
−
To be Released on April 26th.
+
To start this problem, we can first observe. Notice that <math>FGH</math> is a right triangle because angle <math>FGH</math> is supplementary to angle <math>IGE</math> which is a right angle. Therefore, we just have to solve for the length of side <math>FG</math> and <math>HG</math>.
 +
 
 +
Solve for <math>FG</math>:
 +
Triangles <math>AIF</math> and <math>EGF</math> are similar triangles, therefore, we can solve for length <math>AI</math>. <math>AI=AD-ID</math>. Use the technique of sum of squares and square root disintegration, <math>AD=2+\sqrt{2}</math>. Using the same technique, <math>ID=3-\sqrt{2}</math>. <math>AI=2+\sqrt{2}-3+\sqrt{2}=2\sqrt{2}-1</math>. Now, we can set up a ratio.
 +
 
 +
We can set <math>FG=x</math>, so <math>IF=3-\sqrt{2}-x</math>. Using the similar triangle, <math>\frac{GE}{AI}=\frac{FG}{IF}</math>. Plugging the numbers into the ratio, we can get <math>\frac{3-\sqrt{2}}{2\sqrt{2}-1}=\frac{x}{3-\sqrt{2}-x}</math>.
 +
 
 +
<math>~~~~~~~~~~~~~~~~~~~~\frac{3-\sqrt{2}}{2\sqrt{2}-1}=\frac{x}{3-\sqrt{2}-x}</math>
 +
 
 +
<math>~(3-\sqrt{2})(3-\sqrt{2}-x)=x(2\sqrt{2}-1)</math>
 +
 
 +
<math>11-6\sqrt{2}-(3-\sqrt{2})x=x(2\sqrt{2}-1)</math>
 +
 
 +
<math>~~~~~~~~~~~~~~~~~(2+\sqrt{2})x=11-6\sqrt{2}</math>
 +
 
 +
<math>~~~~~~~~~~~~~~~~~~~~~~~~~~~~~x=\frac{11-6\sqrt{2}}{2+\sqrt{2}}</math>
 +
 
 +
<math>~~~~~~~~~~~~~~~~~~~~~~~~~~~~~x=\frac{34-23\sqrt{2}}{2}</math>
 +
 
 +
Solve for <math>HG</math>:
 +
Since angle <math>HEC</math> is <math>90^\circ</math> and angle <math>HCE</math> is <math>45^\circ</math>, <math>EC=HE=2\sqrt{2}-1</math>. Since <math>GE=3-\sqrt{2}</math>, <math>HG=2\sqrt{2}-1-(3-\sqrt{2})=3\sqrt{2}-4</math>.
 +
Finally, we can solve for <math>FH^2</math>, that is, <math>FG^2+HG^2=(\frac{34-23\sqrt{2}}{2})^2+(3\sqrt{2}-4)^2=\frac{1175-830\sqrt{2}}{2}</math>. Therefore, our answer would be <math>1175-830+2+2=\fbox{\textbf{(D)} 349}</math>.

Latest revision as of 13:03, 26 April 2021

In the diagram, $ABCD$ is a square with area $6+4\sqrt{2}$. $AC$ is a diagonal of square $ABCD$. Square $IGED$ has area $11-6\sqrt{2}$. Given that point $J$ bisects line segment $HE$, and $AE$ is a line segment. Extend $EG$ to meet diagonal $AC$ and mark the intersection point $H$. In addition, $K$ is drawn so that $JK//EC$. $FH^2$ can be represented as $\frac{a+b\sqrt{c}}{{d}}$ where $a,b,c,d$ are not necessarily distinct integers. Given that $gcd(a,b,d)=1$, and $c$ does not have a perfect square factor. Find $a+b+c+d$.

24.png

$\textbf{(A)} ~5 \qquad\textbf{(B)} ~15 \qquad\textbf{(C)} ~61 \qquad\textbf{(D)} ~349 \qquad\textbf{(E)} ~2009 \qquad$

Solution

To start this problem, we can first observe. Notice that $FGH$ is a right triangle because angle $FGH$ is supplementary to angle $IGE$ which is a right angle. Therefore, we just have to solve for the length of side $FG$ and $HG$.

Solve for $FG$: Triangles $AIF$ and $EGF$ are similar triangles, therefore, we can solve for length $AI$. $AI=AD-ID$. Use the technique of sum of squares and square root disintegration, $AD=2+\sqrt{2}$. Using the same technique, $ID=3-\sqrt{2}$. $AI=2+\sqrt{2}-3+\sqrt{2}=2\sqrt{2}-1$. Now, we can set up a ratio.

We can set $FG=x$, so $IF=3-\sqrt{2}-x$. Using the similar triangle, $\frac{GE}{AI}=\frac{FG}{IF}$. Plugging the numbers into the ratio, we can get $\frac{3-\sqrt{2}}{2\sqrt{2}-1}=\frac{x}{3-\sqrt{2}-x}$.

$~~~~~~~~~~~~~~~~~~~~\frac{3-\sqrt{2}}{2\sqrt{2}-1}=\frac{x}{3-\sqrt{2}-x}$

$~(3-\sqrt{2})(3-\sqrt{2}-x)=x(2\sqrt{2}-1)$

$11-6\sqrt{2}-(3-\sqrt{2})x=x(2\sqrt{2}-1)$

$~~~~~~~~~~~~~~~~~(2+\sqrt{2})x=11-6\sqrt{2}$

$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~x=\frac{11-6\sqrt{2}}{2+\sqrt{2}}$

$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~x=\frac{34-23\sqrt{2}}{2}$

Solve for $HG$: Since angle $HEC$ is $90^\circ$ and angle $HCE$ is $45^\circ$, $EC=HE=2\sqrt{2}-1$. Since $GE=3-\sqrt{2}$, $HG=2\sqrt{2}-1-(3-\sqrt{2})=3\sqrt{2}-4$. Finally, we can solve for $FH^2$, that is, $FG^2+HG^2=(\frac{34-23\sqrt{2}}{2})^2+(3\sqrt{2}-4)^2=\frac{1175-830\sqrt{2}}{2}$. Therefore, our answer would be $1175-830+2+2=\fbox{\textbf{(D)} 349}$.

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2021_April_MIMC_10_Problems/Problem_22&oldid=152757"