Difference between revisions of "2021 AIME II Problems/Problem 14"
(→Problem) |
m (→Solution 4 (Why Isosceles)) |
||
| (58 intermediate revisions by 10 users not shown) | |||
| Line 2: | Line 2: | ||
Let <math>\Delta ABC</math> be an acute triangle with circumcenter <math>O</math> and centroid <math>G</math>. Let <math>X</math> be the intersection of the line tangent to the circumcircle of <math>\Delta ABC</math> at <math>A</math> and the line perpendicular to <math>GO</math> at <math>G</math>. Let <math>Y</math> be the intersection of lines <math>XG</math> and <math>BC</math>. Given that the measures of <math>\angle ABC, \angle BCA, </math> and <math>\angle XOY</math> are in the ratio <math>13 : 2 : 17, </math> the degree measure of <math>\angle BAC</math> can be written as <math>\frac{m}{n},</math> where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m+n</math>. | Let <math>\Delta ABC</math> be an acute triangle with circumcenter <math>O</math> and centroid <math>G</math>. Let <math>X</math> be the intersection of the line tangent to the circumcircle of <math>\Delta ABC</math> at <math>A</math> and the line perpendicular to <math>GO</math> at <math>G</math>. Let <math>Y</math> be the intersection of lines <math>XG</math> and <math>BC</math>. Given that the measures of <math>\angle ABC, \angle BCA, </math> and <math>\angle XOY</math> are in the ratio <math>13 : 2 : 17, </math> the degree measure of <math>\angle BAC</math> can be written as <math>\frac{m}{n},</math> where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m+n</math>. | ||
| − | == | + | ==Diagram== |
| − | + | <asy> | |
| + | /* Made by MRENTHUSIASM */ | ||
| + | size(375); | ||
| − | ==See | + | pair A, B, C, O, G, X, Y; |
| + | A = origin; | ||
| + | B = (1,0); | ||
| + | C = extension(A,A+10*dir(585/7),B,B+10*dir(180-585/7)); | ||
| + | O = circumcenter(A,B,C); | ||
| + | G = centroid(A,B,C); | ||
| + | Y = intersectionpoint(G--G+(100,0),B--C); | ||
| + | X = intersectionpoint(G--G-(100,0),A--scale(100)*rotate(90)*dir(O-A)); | ||
| + | markscalefactor=3/160; | ||
| + | draw(rightanglemark(O,G,X),red); | ||
| + | dot("$A$",A,1.5*dir(180+585/7),linewidth(4)); | ||
| + | dot("$B$",B,1.5*dir(-585/7),linewidth(4)); | ||
| + | dot("$C$",C,1.5N,linewidth(4)); | ||
| + | dot("$O$",O,1.5N,linewidth(4)); | ||
| + | dot("$G$",G,1.5S,linewidth(4)); | ||
| + | dot("$Y$",Y,1.5E,linewidth(4)); | ||
| + | dot("$X$",X,1.5W,linewidth(4)); | ||
| + | draw(A--B--C--cycle^^X--O--Y--cycle^^A--X^^O--G^^circumcircle(A,B,C)); | ||
| + | </asy> | ||
| + | ~MRENTHUSIASM | ||
| + | |||
| + | ==Solution 1== | ||
| + | In this solution, all angle measures are in degrees. | ||
| + | |||
| + | Let <math>M</math> be the midpoint of <math>\overline{BC}</math> so that <math>\overline{OM}\perp\overline{BC}</math> and <math>A,G,M</math> are collinear. Let <math>\angle ABC=13k,\angle BCA=2k</math> and <math>\angle XOY=17k.</math> | ||
| + | |||
| + | Note that: | ||
| + | <ol style="margin-left: 1.5em;"> | ||
| + | <li>Since <math>\angle OGX = \angle OAX = 90,</math> quadrilateral <math>OGAX</math> is cyclic by the Converse of the Inscribed Angle Theorem.<p>It follows that <math>\angle OAG = \angle OXG,</math> as they share the same intercepted arc <math>\widehat{OG}.</math></li><p> | ||
| + | <li>Since <math>\angle OGY = \angle OMY = 90,</math> quadrilateral <math>OGYM</math> is cyclic by the supplementary opposite angles.<p>It follows that <math>\angle OMG = \angle OYG,</math> as they share the same intercepted arc <math>\widehat{OG}.</math></li><p> | ||
| + | </ol> | ||
| + | Together, we conclude that <math>\triangle OAM \sim \triangle OXY</math> by AA, so <math>\angle AOM = \angle XOY = 17k.</math> | ||
| + | |||
| + | Next, we express <math>\angle BAC</math> in terms of <math>k.</math> By angle addition, we have | ||
| + | <cmath>\begin{align*} | ||
| + | \angle AOM &= \angle AOB + \angle BOM \\ | ||
| + | &= 2\angle BCA + \frac12\angle BOC \hspace{10mm} &&\text{by Inscribed Angle Theorem and Perpendicular Bisector Property} \\ | ||
| + | &= 2\angle BCA + \angle BAC. &&\text{by Inscribed Angle Theorem} | ||
| + | \end{align*}</cmath> | ||
| + | Substituting back gives <math>17k=2(2k)+\angle BAC,</math> from which <math>\angle BAC=13k.</math> | ||
| + | |||
| + | For the sum of the interior angles of <math>\triangle ABC,</math> we get | ||
| + | <cmath>\begin{align*} | ||
| + | \angle ABC + \angle BCA + \angle BAC &= 180 \\ | ||
| + | 13k+2k+13k&=180 \\ | ||
| + | 28k&=180 \\ | ||
| + | k&=\frac{45}{7}. | ||
| + | \end{align*}</cmath> | ||
| + | Finally, we obtain <math>\angle BAC=13k=\frac{585}{7},</math> from which the answer is <math>585+7=\boxed{592}.</math> | ||
| + | |||
| + | ~Constance-variance ~MRENTHUSIASM | ||
| + | |||
| + | ==Solution 2== | ||
| + | Let <math>M</math> be the midpoint of <math>BC</math>. Because <math>\angle{OAX}=\angle{OGX}=\angle{OGY}=\angle{OMY}=90^o</math>, <math>AXOG</math> and <math>OMYG</math> are cyclic, so <math>O</math> is the center of the spiral similarity sending <math>AM</math> to <math>XY</math>, and <math>\angle{XOY}=\angle{AOM}</math>. Because <math>\angle{AOM}=2\angle{BCA}+\angle{BAC}</math>, it's easy to get <math>\frac{585}{7} \implies \boxed{592}</math> from here. | ||
| + | |||
| + | ~Lcz | ||
| + | |||
| + | ==Solution 3 (Easy and Simple)== | ||
| + | Firstly, let <math>M</math> be the midpoint of <math>BC</math>. Then, <math>\angle OMB = 90^o</math>. Now, note that since <math>\angle OGX = \angle XAO = 90^o</math>, quadrilateral <math>AGOX</math> is cyclic. Also, because <math>\angle OMY + \angle OGY = 180^o</math>, <math>OMYG</math> is also cyclic. Now, we define some variables: let <math>\alpha</math> be the constant such that <math>\angle ABC = 13\alpha, \angle ACB = 2\alpha, </math> and <math>\angle XOY = 17\alpha</math>. Also, let <math>\beta = \angle OMG = \angle OYG</math> and <math>\theta = \angle OXG = \angle OAG</math> (due to the fact that <math>AGOX</math> and <math>OMYG</math> are cyclic). Then, <cmath>\angle XOY = 180 - \beta - \theta = 17\alpha \implies \beta + \theta = 180 - 17\alpha.</cmath> Now, because <math>AX</math> is tangent to the circumcircle at <math>A</math>, <math>\angle XAC = \angle CBA = 13\alpha</math>, and <math>\angle CAO = \angle OAX - \angle CAX = 90 - 13\alpha</math>. Finally, notice that <math>\angle AMB = \angle OMB - \angle OMG = 90 - \beta</math>. Then, <cmath>\angle BAM = 180 - \angle ABC - \angle AMB = 180 - 13\alpha - (90 - \beta) = 90 + \beta - 13\alpha.</cmath> Thus, <cmath>\angle BAC = \angle BAM + \angle MAO + \angle OAC = 90 + \beta - 13\alpha + \theta + 90 - 13\alpha = 180 - 26\alpha + (\beta + \theta),</cmath> and <cmath>180 = \angle BAC + 13\alpha + 2\alpha = 180 - 11\alpha + \beta + \theta \implies \beta + \theta = 11\alpha.</cmath> However, from before, <math>\beta+\theta = 180 - 17 \alpha</math>, so <math>11 \alpha = 180 - 17 \alpha \implies 180 = 28 \alpha \implies \alpha = \frac{180}{28}</math>. To finish the problem, we simply compute <cmath>\angle BAC = 180 - 15 \alpha = 180 \cdot \left(1 - \frac{15}{28}\right) = 180 \cdot \frac{13}{28} = \frac{585}{7},</cmath> so our final answer is <math>585+7=\boxed{592}</math>. | ||
| + | |||
| + | ~advanture | ||
| + | |||
| + | ==Solution 4 (Why Isosceles)== | ||
| + | <asy> | ||
| + | /* Made by MRENTHUSIASM */ | ||
| + | size(375); | ||
| + | |||
| + | pair A, B, C, O, G, X, Y; | ||
| + | A = origin; | ||
| + | B = (1,0); | ||
| + | C = extension(A,A+10*dir(585/7),B,B+10*dir(180-585/7)); | ||
| + | O = circumcenter(A,B,C); | ||
| + | G = centroid(A,B,C); | ||
| + | Y = intersectionpoint(G--G+(100,0),B--C); | ||
| + | X = intersectionpoint(G--G-(100,0),A--scale(100)*rotate(90)*dir(O-A)); | ||
| + | pair O1=circumcenter(O,G,A); | ||
| + | real r1=length(O1-O); | ||
| + | markscalefactor=3/160; | ||
| + | filldraw(O--X--Y--cycle, rgb(255,255,0)); | ||
| + | draw(rightanglemark(O,G,X),red); | ||
| + | draw(A--O--B,fuchsia+0.4); | ||
| + | draw(Arc(O1,r1,-40,50),royalblue+0.5); | ||
| + | draw(circumcircle(O,G,Y), heavygreen+0.5); | ||
| + | dot("$A$",A,1.5*dir(180+585/7),linewidth(4)); | ||
| + | dot("$B$",B,1.5*dir(-585/7),linewidth(4)); | ||
| + | dot("$C$",C,1.5N,linewidth(4)); | ||
| + | dot("$O$",O,1.5N,linewidth(4)); | ||
| + | dot("$G$",G,1.5S,linewidth(4)); | ||
| + | dot("$Y$",Y,1.5E,linewidth(4)); | ||
| + | dot("$X$",X,1.5W,linewidth(4)); | ||
| + | draw(A--B--C--cycle^^X--O--Y--cycle^^A--X^^O--G^^circumcircle(A,B,C)); | ||
| + | </asy> | ||
| + | <math>\angle OAX = \angle OGX = 90^\circ \implies</math> quadrilateral <math>XAGO</math> is cyclic <math>\implies</math> | ||
| + | |||
| + | <math>\angle GXO = \angle GAO,</math> as they share the same intersept <math>\overset{\Large\frown} {GO}.</math> | ||
| + | |||
| + | <math>\angle OGY = \angle OMY = 90^\circ \implies</math> quadrilateral <math>OGYM</math> is cyclic <math>\implies</math> | ||
| + | |||
| + | <math>\angle GYO = \angle OMG,</math> as they share the same intercept <math>\overset{\Large\frown} {GO}.</math> | ||
| + | |||
| + | In triangles <math>\triangle XOY</math> and <math>\triangle AOM,</math> two pairs of angles are equal, which means that the third angles <math>\angle XOY = \angle AOM</math> are also equal. | ||
| + | |||
| + | <math>\angle ABC : \angle BCA : \angle AOM = 13 : 2 : 17,</math> so <math>\angle AOM = \angle ABC + 2 \angle BCA.</math> | ||
| + | |||
| + | According to the <i><b>Claim</b></i>, <math>\triangle ABC</math> is isosceles, | ||
| + | <cmath>\angle ABC : \angle BCA : \angle BAC = 13 : 2 : 13.</cmath> | ||
| + | <cmath>\angle BAC = \frac{13} {13 + 2 + 13} \cdot 180^\circ = \frac {585^\circ}{7} \implies 585 + 7 = \boxed{592}.</cmath> | ||
| + | |||
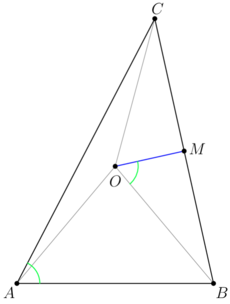
| + | [[File:AIME-II-2021-14.png|230px|right]] | ||
| + | <i><b>Claim</b></i> | ||
| + | |||
| + | Let <math>\triangle ABC</math> be an acute triangle with circumcenter <math>O.</math> | ||
| + | |||
| + | Let <math>M</math> be the midpoint of <math>BC</math> so <math>MO\perp BC.</math> | ||
| + | |||
| + | If <math>\angle AOM = 2\angle ACB + \angle ABC,</math> then <math>AC = BC.</math> | ||
| + | |||
| + | We define <math>\angle AOM</math> as the sum of <math>\angle AOB + \angle BOM,</math> this angle can be greater than <math>180^\circ.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | <math>\angle BAC = \angle BOM</math> as they share the same intercept <math>\overset{\Large\frown} {BC}</math> (an inscribed angle and half of central angle). | ||
| + | |||
| + | <math>\angle AOB = 2\angle ACB</math> as they share the same intercept <math>\overset{\Large\frown} {AB}.</math> | ||
| + | |||
| + | <cmath>\angle AOM = \angle AOB + \angle BOM = 2 \angle ACB + \angle CAB.</cmath> | ||
| + | |||
| + | If <math>\angle AOM = 2 \angle ACB + \angle ABC,</math> then <math>\angle ABC = \angle CAB, AC = BC.</math> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Solution 5== | ||
| + | |||
| + | Extend <math>XA</math> and meet line <math>CB</math> at <math>P</math>. Extend <math>AG</math> to meet <math>BC</math> at <math>F</math>. Since <math>AF</math> is the median from <math>A</math> to <math>BC</math>, <math>A,G,F</math> are collinear. Furthermore, <math>OF</math> is perpendicular to <math>BC</math> | ||
| + | |||
| + | Draw the circumcircle of <math>\triangle{XPY}</math>, as <math>OA\bot XP, OG\bot XY, OF\bot PY</math>, <math>A,G,F</math> are collinear, <math>O</math> lies on <math>(XYP)</math> as <math>AGF</math> is the Simson line of <math>O</math> with respect to <math>\triangle{XPY}</math>. Thus, <math>\angle{P}=180-17x, \angle{PAB}=\angle{C}=2x, 180-15x=13x, x=\frac{45}{7}</math>, the answer is <math>180-15\cdot \frac{45}{7}=\frac{585}{7}</math> which is <math>\boxed{592}</math>. | ||
| + | |||
| + | ~bluesoul | ||
| + | |||
| + | ==Video Solution 1== | ||
| + | https://www.youtube.com/watch?v=zFH1Z7Ydq1s | ||
| + | |||
| + | ~Mathematical Dexterity | ||
| + | |||
| + | ==Video Solution 2== | ||
| + | https://www.youtube.com/watch?v=7Bxr2h4btWo | ||
| + | |||
| + | ~Osman Nal | ||
| + | |||
| + | ==Video Solution by Interstigation== | ||
| + | https://www.youtube.com/watch?v=yIWe7ME6fpA | ||
| + | |||
| + | ~Interstigation | ||
| + | |||
| + | ==See Also== | ||
{{AIME box|year=2021|n=II|num-b=13|num-a=15}} | {{AIME box|year=2021|n=II|num-b=13|num-a=15}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Latest revision as of 15:50, 25 December 2022
Contents
Problem
Let ![]() be an acute triangle with circumcenter
be an acute triangle with circumcenter ![]() and centroid
and centroid ![]() . Let
. Let ![]() be the intersection of the line tangent to the circumcircle of
be the intersection of the line tangent to the circumcircle of ![]() at
at ![]() and the line perpendicular to
and the line perpendicular to ![]() at
at ![]() . Let
. Let ![]() be the intersection of lines
be the intersection of lines ![]() and
and ![]() . Given that the measures of
. Given that the measures of ![]() and
and ![]() are in the ratio
are in the ratio ![]() the degree measure of
the degree measure of ![]() can be written as
can be written as ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Diagram
![[asy] /* Made by MRENTHUSIASM */ size(375); pair A, B, C, O, G, X, Y; A = origin; B = (1,0); C = extension(A,A+10*dir(585/7),B,B+10*dir(180-585/7)); O = circumcenter(A,B,C); G = centroid(A,B,C); Y = intersectionpoint(G--G+(100,0),B--C); X = intersectionpoint(G--G-(100,0),A--scale(100)*rotate(90)*dir(O-A)); markscalefactor=3/160; draw(rightanglemark(O,G,X),red); dot("$A$",A,1.5*dir(180+585/7),linewidth(4)); dot("$B$",B,1.5*dir(-585/7),linewidth(4)); dot("$C$",C,1.5N,linewidth(4)); dot("$O$",O,1.5N,linewidth(4)); dot("$G$",G,1.5S,linewidth(4)); dot("$Y$",Y,1.5E,linewidth(4)); dot("$X$",X,1.5W,linewidth(4)); draw(A--B--C--cycle^^X--O--Y--cycle^^A--X^^O--G^^circumcircle(A,B,C)); [/asy]](http://latex.artofproblemsolving.com/f/0/5/f0519e337893dd856908a43b2cb78725f49b65ef.png) ~MRENTHUSIASM
~MRENTHUSIASM
Solution 1
In this solution, all angle measures are in degrees.
Let ![]() be the midpoint of
be the midpoint of ![]() so that
so that ![]() and
and ![]() are collinear. Let
are collinear. Let ![]() and
and ![]()
Note that:
- Since
 quadrilateral
quadrilateral  is cyclic by the Converse of the Inscribed Angle Theorem.
is cyclic by the Converse of the Inscribed Angle Theorem.It follows that
 as they share the same intercepted arc
as they share the same intercepted arc 
- Since
 quadrilateral
quadrilateral  is cyclic by the supplementary opposite angles.
is cyclic by the supplementary opposite angles.It follows that
 as they share the same intercepted arc
as they share the same intercepted arc 
Together, we conclude that ![]() by AA, so
by AA, so ![]()
Next, we express ![]() in terms of
in terms of ![]() By angle addition, we have
By angle addition, we have
 Substituting back gives
Substituting back gives ![]() from which
from which ![]()
For the sum of the interior angles of ![]() we get
we get
 Finally, we obtain
Finally, we obtain ![]() from which the answer is
from which the answer is ![]()
~Constance-variance ~MRENTHUSIASM
Solution 2
Let ![]() be the midpoint of
be the midpoint of ![]() . Because
. Because ![]() ,
, ![]() and
and ![]() are cyclic, so
are cyclic, so ![]() is the center of the spiral similarity sending
is the center of the spiral similarity sending ![]() to
to ![]() , and
, and ![]() . Because
. Because ![]() , it's easy to get
, it's easy to get ![]() from here.
from here.
~Lcz
Solution 3 (Easy and Simple)
Firstly, let ![]() be the midpoint of
be the midpoint of ![]() . Then,
. Then, ![]() . Now, note that since
. Now, note that since ![]() , quadrilateral
, quadrilateral ![]() is cyclic. Also, because
is cyclic. Also, because ![]() ,
, ![]() is also cyclic. Now, we define some variables: let
is also cyclic. Now, we define some variables: let ![]() be the constant such that
be the constant such that ![]() and
and ![]() . Also, let
. Also, let ![]() and
and ![]() (due to the fact that
(due to the fact that ![]() and
and ![]() are cyclic). Then,
are cyclic). Then, ![]() Now, because
Now, because ![]() is tangent to the circumcircle at
is tangent to the circumcircle at ![]() ,
, ![]() , and
, and ![]() . Finally, notice that
. Finally, notice that ![]() . Then,
. Then, ![]() Thus,
Thus, ![]() and
and ![]() However, from before,
However, from before, ![]() , so
, so ![]() . To finish the problem, we simply compute
. To finish the problem, we simply compute ![]() so our final answer is
so our final answer is ![]() .
.
~advanture
Solution 4 (Why Isosceles)
![[asy] /* Made by MRENTHUSIASM */ size(375); pair A, B, C, O, G, X, Y; A = origin; B = (1,0); C = extension(A,A+10*dir(585/7),B,B+10*dir(180-585/7)); O = circumcenter(A,B,C); G = centroid(A,B,C); Y = intersectionpoint(G--G+(100,0),B--C); X = intersectionpoint(G--G-(100,0),A--scale(100)*rotate(90)*dir(O-A)); pair O1=circumcenter(O,G,A); real r1=length(O1-O); markscalefactor=3/160; filldraw(O--X--Y--cycle, rgb(255,255,0)); draw(rightanglemark(O,G,X),red); draw(A--O--B,fuchsia+0.4); draw(Arc(O1,r1,-40,50),royalblue+0.5); draw(circumcircle(O,G,Y), heavygreen+0.5); dot("$A$",A,1.5*dir(180+585/7),linewidth(4)); dot("$B$",B,1.5*dir(-585/7),linewidth(4)); dot("$C$",C,1.5N,linewidth(4)); dot("$O$",O,1.5N,linewidth(4)); dot("$G$",G,1.5S,linewidth(4)); dot("$Y$",Y,1.5E,linewidth(4)); dot("$X$",X,1.5W,linewidth(4)); draw(A--B--C--cycle^^X--O--Y--cycle^^A--X^^O--G^^circumcircle(A,B,C)); [/asy]](http://latex.artofproblemsolving.com/f/3/d/f3d6ab62d1347c45ceff8db374fe66f738a8e33d.png)
![]() quadrilateral
quadrilateral ![]() is cyclic
is cyclic ![]()
![]() as they share the same intersept
as they share the same intersept ![]()
![]() quadrilateral
quadrilateral ![]() is cyclic
is cyclic ![]()
![]() as they share the same intercept
as they share the same intercept ![]()
In triangles ![]() and
and ![]() two pairs of angles are equal, which means that the third angles
two pairs of angles are equal, which means that the third angles ![]() are also equal.
are also equal.
![]() so
so ![]()
According to the Claim, ![]() is isosceles,
is isosceles,
![]()
![]()
Claim
Let ![]() be an acute triangle with circumcenter
be an acute triangle with circumcenter ![]()
Let ![]() be the midpoint of
be the midpoint of ![]() so
so ![]()
If ![]() then
then ![]()
We define ![]() as the sum of
as the sum of ![]() this angle can be greater than
this angle can be greater than ![]()
Proof
![]() as they share the same intercept
as they share the same intercept ![]() (an inscribed angle and half of central angle).
(an inscribed angle and half of central angle).
![]() as they share the same intercept
as they share the same intercept ![]()
![]()
If ![]() then
then ![]()
vladimir.shelomovskii@gmail.com, vvsss
Solution 5
Extend ![]() and meet line
and meet line ![]() at
at ![]() . Extend
. Extend ![]() to meet
to meet ![]() at
at ![]() . Since
. Since ![]() is the median from
is the median from ![]() to
to ![]() ,
, ![]() are collinear. Furthermore,
are collinear. Furthermore, ![]() is perpendicular to
is perpendicular to ![]()
Draw the circumcircle of ![]() , as
, as ![]() ,
, ![]() are collinear,
are collinear, ![]() lies on
lies on ![]() as
as ![]() is the Simson line of
is the Simson line of ![]() with respect to
with respect to ![]() . Thus,
. Thus, ![]() , the answer is
, the answer is ![]() which is
which is ![]() .
.
~bluesoul
Video Solution 1
https://www.youtube.com/watch?v=zFH1Z7Ydq1s
~Mathematical Dexterity
Video Solution 2
https://www.youtube.com/watch?v=7Bxr2h4btWo
~Osman Nal
Video Solution by Interstigation
https://www.youtube.com/watch?v=yIWe7ME6fpA
~Interstigation
See Also
| 2021 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 13 |
Followed by Problem 15 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.