Difference between revisions of "2021 AIME I Problems/Problem 9"

Latest revision as of 17:16, 25 January 2024

1 Problem
2 Diagram
3 Solution 1 (Similar Triangles and Pythagorean Theorem)
4 Solution 2 (Similar Triangles and Pythagorean Theorem)
5 Solution 3 (Similar Triangles and Pythagorean Theorem)
6 Solution 4 (Cyclic Quadrilaterals, Similar Triangles, Pythagorean Theorem)
7 Solution 5 (Cyclic Quadrilaterals, Similar Triangles, Pythagorean Theorem)
8 Solution 6 (Similar Triangles and Trigonometry)
9 Solution 7 (Similar Triangles and Trigonometry)
10 Solution 8 (Heron's Formula)
11 Solution 9 (Three Heights)
12 Solution 10 (Area)
13 Video Solution
14 Video Solution
15 See Also

Problem

Let $ABCD$ be an isosceles trapezoid with $AD=BC$ and $AB<CD.$ Suppose that the distances from $A$ to the lines $BC,CD,$ and $BD$ are $15,18,$ and $10,$ respectively. Let $K$ be the area of $ABCD.$ Find $\sqrt2 \cdot K.$

Diagram

$[asy] /* Made by MRENTHUSIASM */ size(250); pair A, B, C, D, E, F, G, H; A = (-45sqrt(2)/8,18); B = (45sqrt(2)/8,18); C = (81sqrt(2)/8,0); D = (-81sqrt(2)/8,0); E = foot(A,C,B); F = foot(A,C,D); G = foot(A,B,D); H = intersectionpoint(A--F,B--D); markscalefactor=0.1; draw(rightanglemark(A,E,B),red); draw(rightanglemark(A,F,C),red); draw(rightanglemark(A,G,D),red); dot("$A$",A,1.5*NW,linewidth(4)); dot("$B$",B,1.5*NE,linewidth(4)); dot("$C$",C,1.5*SE,linewidth(4)); dot("$D$",D,1.5*SW,linewidth(4)); dot(E,linewidth(4)); dot(F,linewidth(4)); dot(G,linewidth(4)); draw(A--B--C--D--cycle^^B--D^^B--E); draw(A--E^^A--F^^A--G,dashed); label("$10$",midpoint(A--G),1.5*(1,0)); label("$15$",midpoint(A--E),1.5*N); Label L = Label("$18$", align=(0,0), position=MidPoint, filltype=Fill(0,3,white)); draw(C+(5,0)--(81sqrt(2)/8,18)+(5,0), L=L, arrow=Arrows(),bar=Bars(15)); [/asy]$ ~MRENTHUSIASM

Solution 1 (Similar Triangles and Pythagorean Theorem)

Let $\overline{AE}, \overline{AF},$ and $\overline{AG}$ be the perpendiculars from $A$ to $\overleftrightarrow{BC}, \overleftrightarrow{CD},$ and $\overleftrightarrow{BD},$ respectively. Next, let $H$ be the intersection of $\overline{AF}$ and $\overline{BD}.$

We set $AB=x$ and $AH=y,$ as shown below. $[asy] /* Made by MRENTHUSIASM */ size(250); pair A, B, C, D, E, F, G, H; A = (-45sqrt(2)/8,18); B = (45sqrt(2)/8,18); C = (81sqrt(2)/8,0); D = (-81sqrt(2)/8,0); E = foot(A,C,B); F = foot(A,C,D); G = foot(A,B,D); H = intersectionpoint(A--F,B--D); markscalefactor=0.1; draw(rightanglemark(A,E,B),red); draw(rightanglemark(A,F,C),red); draw(rightanglemark(A,G,D),red); dot("$A$",A,1.5*NW,linewidth(4)); dot("$B$",B,1.5*NE,linewidth(4)); dot("$C$",C,1.5*SE,linewidth(4)); dot("$D$",D,1.5*SW,linewidth(4)); dot("$E$",E,1.5*dir(E),linewidth(4)); dot("$F$",F,1.5*S,linewidth(4)); dot("$G$",G,SE,linewidth(4)); dot("$H$",H,SE,linewidth(4)); draw(A--B--C--D--cycle^^B--D^^B--E); draw(A--E^^A--F^^A--G,dashed); label("$10$",midpoint(A--G),1.5*(1,0)); label("$15$",midpoint(A--E),1.5*N); Label L = Label("$18$", align=(0,0), position=MidPoint, filltype=Fill(0,3,white)); draw(C+(5,0)--(81sqrt(2)/8,18)+(5,0), L=L, arrow=Arrows(),bar=Bars(15)); label("$x$",midpoint(A--B),N); label("$y$",midpoint(A--H),W); [/asy]$ From here, we obtain $HF=18-y$ by segment subtraction, and $BG=\sqrt{x^2-10^2}$ and $HG=\sqrt{y^2-10^2}$ by the Pythagorean Theorem.

Since $\angle ABG$ and $\angle HAG$ are both complementary to $\angle AHB,$ we have $\angle ABG = \angle HAG,$ from which $\triangle ABG \sim \triangle HAG$ by AA. It follows that $\frac{BG}{AG}=\frac{AG}{HG},$ so $BG\cdot HG=AG^2,$ or $\sqrt{x^2-10^2}\cdot\sqrt{y^2-10^2}=10^2. \hspace{10mm} (1)$ Since $\angle AHB = \angle FHD$ by vertical angles, we have $\triangle AHB \sim \triangle FHD$ by AA, with the ratio of similitude $\frac{AH}{FH}=\frac{BA}{DF}.$ It follows that $DF=BA\cdot\frac{FH}{AH}=x\cdot\frac{18-y}{y}.$

Since $\angle EBA = \angle ECD = \angle FDA$ by angle chasing, we have $\triangle EBA \sim \triangle FDA$ by AA, with the ratio of similitude $\frac{EA}{FA}=\frac{BA}{DA}.$ It follows that $DA=BA\cdot\frac{FA}{EA}=x\cdot\frac{18}{15}=\frac{6}{5}x.$

By the Pythagorean Theorem on right $\triangle ADF,$ we have $DF^2+AF^2=AD^2,$ or $\left(x\cdot\frac{18-y}{y}\right)^2+18^2=\left(\frac{6}{5}x\right)^2. \hspace{7mm} (2)$ Solving this system of equations ( $(1)$ and $(2)$ ), we get $x=\frac{45\sqrt2}{4}$ and $y=\frac{90}{7},$ so $AB=x=\frac{45\sqrt2}{4}$ and $CD=AB+2DF=x+2\left(x\cdot\frac{18-y}{y}\right)=\frac{81\sqrt2}{4}.$ Finally, the area of $ABCD$ is $K=\frac{AB+CD}{2}\cdot AF=\frac{567\sqrt2}{2},$ from which $\sqrt2 \cdot K=\boxed{567}.$

~MRENTHUSIASM

Remark

Instead of solving the system of equations $(1)$ and $(2),$ which can be time consuming, by noting that $\triangle ACF \sim \triangle ABG$ by AA, we could find out $\frac{AB}{AG} = \frac{AC}{AF}$ , which gives $AC = \frac{9}{5}x$ . We also know that $EB = \sqrt{x^2 - 15^2}$ by Pythagorean Theorem on $\triangle ABE$ . From $BC = AD = \frac{6}{5}x,$ we apply the Pythagorean Theorem to $\triangle ACE$ and obtain $AC^2 = (EB+BC)^2 + AE^2.$ Substituting, we get $\frac{81}{25}x^2 = \left(\sqrt{x^2 -225}+\frac{6}{5}x\right)^2+225 \iff x = 3\sqrt{x^2 - 15^2},$ from which $x = \frac{45\sqrt{2}}{4}.$

~Chupdogs

Solution 2 (Similar Triangles and Pythagorean Theorem)

First, draw the diagram. Then, notice that since $ABCD$ is isosceles, $\Delta ABD \cong \Delta BAC$ , and the length of the altitude from $B$ to $AC$ is also $10$ . Let the foot of this altitude be $F$ , and let the foot of the altitude from $A$ to $BC$ be denoted as $E$ . Then, $\Delta BCF \sim \Delta ACE$ . So, $\frac{BC}{AC} = \frac{BF}{AE} = \frac{2}{3}$ . Now, notice that $[ABC] = \frac{10 \cdot AC} {2} = \frac{AB \cdot 18}{2} \implies AC = \frac{9 \cdot AB}{5}$ , where $[ABC]$ denotes the area of triangle $ABC$ . Letting $AB = x$ , this equality becomes $AC = \frac{9x}{5}$ . Also, from $\frac{BC}{AC} = \frac{2}{3}$ , we have $BC = \frac{6x}{5}$ . Now, by the Pythagorean theorem on triangles $ABF$ and $CBF$ , we have $AF = \sqrt{x^{2}-100}$ and $CF = \sqrt{ \left( \frac{6x}{5} \right) ^{2}-100}$ . Notice that $AC = AF + CF$ , so $\frac{9x}{5} = \sqrt{x^{2}-100} + \sqrt{ \left( \frac{6x}{5} \right) ^{2}-100}$ . Squaring both sides of the equation once, moving $x^{2}-100$ and $\left( \frac{6x}{5} \right) ^{2}-100$ to the right, dividing both sides by $2$ , and squaring the equation once more, we are left with $\frac{32x^{4}}{25} = 324x^{2}$ . Dividing both sides by $x^{2}$ (since we know $x$ is positive), we are left with $\frac{32x^{2}}{25} = 324$ . Solving for $x$ gives us $x = \frac{45}{2\sqrt{2}}$ .

Now, let the foot of the perpendicular from $A$ to $CD$ be $G$ . Then let $DG = y$ . Let the foot of the perpendicular from $B$ to $CD$ be $H$ . Then, $CH$ is also equal to $y$ . Notice that $ABHG$ is a rectangle, so $GH = x$ . Now, we have $CG = GH + CH = x + y$ . By the Pythagorean theorem applied to $\Delta AGC$ , we have $(x+y)^{2}+18^{2}= \left( \frac{9x}{5} \right) ^{2}$ . We know that $\frac{9x}{5} = \frac{9}{5} \cdot \frac{45}{2\sqrt{2}} = \frac{81}{2\sqrt{2}}$ , so we can plug this into this equation. Solving for $x+y$ , we get $x+y=\frac{63}{2\sqrt{2}}$ .

Finally, to find $[ABCD]$ , we use the formula for the area of a trapezoid: $K = [ABCD] = \frac{b_{1}+b_{2}}{2} \cdot h = \frac{AB+CD}{2} \cdot 18 = \frac{x+(CG+DG)}{2} \cdot 18 = \frac{2x+2y}{2} \cdot 18 = (x+y) \cdot 18 = \frac{63}{2\sqrt{2}} \cdot 18 = \frac{567}{\sqrt{2}}$ . The problem asks us for $K \cdot \sqrt{2}$ , which comes out to be $\boxed{567}$ .

~advanture

Solution 3 (Similar Triangles and Pythagorean Theorem)

Make $AE$ perpendicular to $BC$ ; $AG$ perpendicular to $BD$ ; $AF$ perpendicular $DC$ .

It's obvious that $\triangle{AEB} \sim \triangle{AFD}$ . Let $EB=5x; AB=5y; DF=6x; AD=6y$ . Then make $BQ$ perpendicular to $DC$ , it's easy to get $BQ=18$ .

Since $AB$ parallel to $DC$ , $\angle{ABG}=\angle{BDQ}$ , so $\triangle{ABG} \sim \triangle{BDQ}$ . After drawing the altitude, it's obvious that $FQ=AB=5y$ , so $DQ=5y+6x$ . According to the property of similar triangles, $AG/BQ=BG/DQ$ . So, $\frac{5}{9}=\frac{GB}{(6x+5y)}$ , or $GB=\frac{(30x+25y)}{9}$ .

Now, we see the $\triangle AEB$ , pretty easy to find that $15^2+(5x)^2=(5y)^2$ , then we get $x^2+9=y^2$ , then express $y$ into $x$ form that $y=\sqrt{x^2+9}$ we put the length of $BG$ back to $\triangle AGB$ : $BG^2+100=AB^2$ . So, $\frac{[30x+25\sqrt{(x^2+9)}]^2}{81}+100=(5\sqrt{x^2+9})^2.$ After calculating, we can have a final equation of $x^2+9=\sqrt{x^2+9}\cdot3x$ . It's easy to find $x=\frac{3\sqrt{2}}{4}$ then $y=\frac{9\sqrt{2}}{4}$ . So, $\sqrt{2}\cdot K = \sqrt{2}\cdot(5y+5y+6x+6x)\cdot9=\boxed{567}.$ ~bluesoul

Solution 4 (Cyclic Quadrilaterals, Similar Triangles, Pythagorean Theorem)

Let the foot of the altitude from $A$ to $BC$ be $P$ , to $CD$ be $Q$ , and to $BD$ be $R$ .

Note that all isosceles trapezoids are cyclic quadrilaterals; thus, $A$ is on the circumcircle of $\triangle BCD$ and we have that $PRQ$ is the Simson Line from $A$ . As $\angle QAB = 90^\circ$ , we have that $\angle QAR = 90^\circ - \angle RAB =\angle ABR = \angle APR = \angle APQ$ , with the last equality coming from cyclic quadrilateral $APBR$ . Thus, $\triangle QAR \sim \triangle QPA$ and we have that $\frac{AQ}{AR} = \frac{PQ}{PA}$ or that $\frac{18}{10} = \frac{QP}{15}$ , which we can see gives us that $QP = 27$ . Further ratios using the same similar triangles gives that $QR = \frac{25}{3}$ and $RP = \frac{56}{3}$ .

We also see that quadrilaterals $APBR$ and $ARQD$ are both cyclic, with diameters of the circumcircles being $AB$ and $AD$ respectively. The intersection of the circumcircles are the points $A$ and $R$ , and we know $DRB$ and $QRP$ are both line segments passing through an intersection of the two circles with one endpoint on each circle. By Fact 5, we know then that there exists a spiral similarity with center $A$ taking $\triangle APQ$ to $\triangle APD$ . Because we know a lot about $\triangle APQ$ but very little about $\triangle APD$ and we would like to know more, we wish to find the ratio of similitude between the two triangles.

To do this, we use the one number we have for $\triangle APD$ : we know that the altitude from $A$ to $BD$ has length $10$ . As the two triangles are similar, if we can find the height from $A$ to $PQ$ , we can take the ratio of the two heights as the ratio of similitude. To do this, we once again note that $QP = 27$ . Using this, we can drop the altitude from $A$ to $QP$ and let it intersect $QP$ at $H$ . Then, let $QH = x$ and thus $HP=27-x$ . We then have by the Pythagorean Theorem on $\triangle AQH$ and $\triangle APH$ : $\begin{align*} 15^2 - x^2 &= 18^2 - (27-x)^2 \\ 225 - x^2 &= 324 - (x^2-54x+729) \\ 54x &= 630 \\ x &= \frac{35}{3}. \end{align*}$ Then, $RH = QH - QR = \frac{35}{3} - \frac{25}{3} = \frac{10}{3}$ . This gives us then from right triangle $\triangle ARH$ that $AH = \frac{20\sqrt{2}}{3}$ and thus the ratio of $\triangle APQ$ to $\triangle ABD$ is $\frac{3\sqrt{2}}{4}$ . From this, we see then that $AB = AP \cdot \frac{3\sqrt{2}}{4} = 15 \cdot \frac{3\sqrt{2}}{4} = \frac{45\sqrt{2}}{4}$ and $AD = AQ \cdot \frac{3\sqrt{2}}{4} = 18 \cdot \frac{3\sqrt{2}}{4} = \frac{27\sqrt{2}}{2}.$ The Pythagorean Theorem on $\triangle AQD$ then gives that $QD = \sqrt{AD^2 - AQ^2} = \sqrt{\left(\frac{27\sqrt{2}}{2}\right)^2 - 18^2} = \sqrt{\frac{81}{2}} = \frac{9\sqrt{2}}{2}.$ Then, we have the height of trapezoid $ABCD$ is $AQ = 18$ , the top base is $AB = \frac{45\sqrt{2}}{4}$ , and the bottom base is $CD = \frac{45\sqrt{2}}{4} + 2\cdot\frac{9\sqrt{2}}{2}$ . From the equation of a trapezoid, $K = \frac{b_1+b_2}{2} \cdot h = \frac{63\sqrt{2}}{4} \cdot 18 = \frac{567\sqrt{2}}{2}$ , so the answer is $K\sqrt{2} = \boxed{567}$ .

~lvmath

Solution 5 (Cyclic Quadrilaterals, Similar Triangles, Pythagorean Theorem)

Let $E,F,$ and $G$ be the feet of the altitudes from $A$ to $BC,CD,$ and $DB$ , respectively.

Claim: We have $2$ pairs of similar right triangles: $\triangle AEB \sim \triangle AFD$ and $\triangle AGD \sim \triangle AEC$ .

Proof: Note that $ABCD$ is cyclic. We need one more angle, and we get this from this cyclic quadrilateral: $\begin{align*} \angle ABE &= 180^\circ - \angle ABC =\angle ADC = \angle ADG, \\ \angle ADG &= \angle ADB =\angle ACB = \angle ACE. \hspace{20mm} \square \end{align*}$ Let $AD=a$ . We obtain from the similarities $AB = \frac{5a}{6}$ and $AC=BD=\frac{3a}{2}$ .

By Ptolemy, $\left(\frac{3a}{2}\right)^2 = a^2 + \frac{5a}{6} \cdot CD$ , so $\frac{5a^2}{4} = \frac{5a}{6} \cdot CD$ .

We obtain $CD=\frac{3a}{2}$ , so $DF=\frac{CD-AB}{2}=\frac{a}{3}$ .

Applying the Pythagorean theorem on $\triangle ADF$ , we get $324=a^2 - \frac{a^2}{9}=\frac{8a^2}{9}$ .

Thus, $a=\frac{27}{\sqrt{2}}$ , and $[ABCD]=\frac{AB+CD}{2} \cdot 18 = \frac{\frac{5a}{6} +\frac{9a}{6}}{2} \cdot 18 = 18 \cdot \frac{7}{6} \cdot \frac{27}{\sqrt{2}} = \frac{567}{\sqrt{2}}$ , yielding $\sqrt2\cdot[ABCD]=\boxed{567}$ .

Solution 6 (Similar Triangles and Trigonometry)

Let $AD=BC=a$ . Draw diagonal $AC$ and let $G$ be the foot of the perpendicular from $B$ to $AC$ , $F$ be the foot of the perpendicular from $A$ to line $BC$ , and $H$ be the foot of the perpendicular from $A$ to $DC$ .

Note that $\triangle CBG\sim\triangle CAF$ , and we get that $\frac{10}{15}=\frac{a}{AC}$ . Therefore, $AC=\frac32 a$ . It then follows that $\triangle ABF\sim\triangle ADH$ . Using similar triangles, we can then find that $AB=\frac{5}{6}a$ . Using the Law of Cosines on $\triangle ABC$ , We can find that the $\cos\angle ABC=-\frac{1}{3}$ . Since $\angle ABF=\angle ADH$ , and each is supplementary to $\angle ABC$ , we know that the $\cos\angle ADH=\frac{1}{3}$ . It then follows that $a=\frac{27\sqrt{2}}{2}$ . Then it can be found that the area $K$ is $\frac{567\sqrt{2}}{2}$ . Multiplying this by $\sqrt{2}$ , the answer is $\boxed{567}$ .

~happykeeper

Solution 7 (Similar Triangles and Trigonometry)

Draw the distances in terms of $B$ , as shown in the diagram. By similar triangles, $\triangle{AEC}\sim\triangle{BIC}$ . As a result, let $AB=u$ , then $BC=AD=\frac{6}{5}u$ and $2AC=3BC$ . The triangle $ABC$ is $6-5-9$ which $\cos(\angle{ABC})=-\frac{1}{3}$ . By angle subtraction, $\cos(180-\theta)=-\cos\theta$ . Therefore, $AB=\frac{45}{2\sqrt{2}}=\frac{45\sqrt{2}}{4}$ and $AD=BC=\frac{27}{\sqrt{2}}$ . By trapezoid area formula, the area of $ABCD$ is equal to $(AB+DF)\cdot 18=567\cdot \frac{\sqrt{2}}{2}$ which $\sqrt{2}\cdot k=\boxed{567}$ .

~math2718281828459

Solution 8 (Heron's Formula)

$[asy] size(250); pair A, B, C, D, E, F, G, H; A = (-45sqrt(2)/8,18); B = (45sqrt(2)/8,18); C = (81sqrt(2)/8,0); D = (-81sqrt(2)/8,0); E = foot(A,C,B); F = foot(A,C,D); G = foot(A,B,D); H = intersectionpoint(A--F,B--D); markscalefactor=0.1; draw(rightanglemark(A,E,B),red); draw(rightanglemark(A,F,C),red); draw(rightanglemark(A,G,D),red); filldraw(A--D--F--cycle,yellow,black+linewidth(1.5)); filldraw(A--B--E--cycle,yellow,black+linewidth(1.5)); dot("$A$",A,1.5*NW,linewidth(4)); dot("$B$",B,1.5*NE,linewidth(4)); dot("$C$",C,1.5*SE,linewidth(4)); dot("$D$",D,1.5*SW,linewidth(4)); dot(E,linewidth(4)); dot(F,linewidth(4)); dot(G,linewidth(4)); label("$E$",E,NE); label("$F$",F, S); label("$G$",G,SE); draw(A--B--C--D--cycle^^B--D^^B--E); draw(A--E^^A--F^^A--G,dashed); label("$10$",midpoint(A--G),1.5*(1,0)); label("$15$",midpoint(A--E),1.5*N); label("$5x$",midpoint(A--B),S); label("$6x$",midpoint(A--D),1.5*(-1,0)); Label L = Label("$18$", align=(0,0), position=MidPoint, filltype=Fill(0,3,white)); draw(C+(5,0)--(81sqrt(2)/8,18)+(5,0), L=L, arrow=Arrows(),bar=Bars(15)); [/asy]$ Let the points formed by dropping altitudes from $A$ to the lines $BC$ , $CD$ , and $BD$ be $E$ , $F$ , and $G$ , respectively.

We have $\triangle ABE \sim \triangle ADF \implies \frac{AD}{18} = \frac{AB}{15} \implies AD = \frac{6}{5}AB$ and $BD\cdot10 = 2[ABD] = AB\cdot18 \implies BD = \frac{9}{5}AB.$ For convenience, let $AB = 5x$ . By Heron's formula on $\triangle ABD$ , we have sides $5x,6x,9x$ and semiperimeter $10x$ , so $\sqrt{10x\cdot5x\cdot4x\cdot1x} = [ABD] = \frac{AB\cdot18}{2} = 45x \implies 10\sqrt{2}x^2 = 45x \implies x= \frac{45}{10\sqrt{2}},$ so $AB = 5x = \frac{45}{2\sqrt{2}}$ .

Then, $BE = \sqrt{AB^2 - CA^2} = \sqrt{\left(\frac{45}{2\sqrt{2}}\right)^2 - 15^2} = \sqrt{\frac{225}{8}} = \frac{15}{2\sqrt{2}}$ and $\triangle ABE \sim \triangle ADF \implies DF = \frac{6}{5}BE = \frac{6}{5}\cdot\frac{15}{2\sqrt{2}} = \frac{18}{2\sqrt{2}}.$ Finally, recalling that $ABCD$ is isosceles, $K = [ABCD] = \frac{18}{2}(AB + (AB + 2DF)) = 18(AB + DF) = 18\left(\frac{45}{2\sqrt{2}} + \frac{18}{2\sqrt{2}}\right) = \frac{567}{\sqrt{2}},$ so $\sqrt{2}\cdot K = \boxed{567}$ .

~emerald_block

Solution 9 (Three Heights)

Let $\overline{AE}, \overline{AF},$ and $\overline{AG}$ be the perpendiculars from $A$ to ${BC}, {CD},$ and ${BD},$ respectively. $AE = 15, AF = 18, AG =10$ . Denote by $G'$ the base of the perpendicular from $B$ to $AC, H$ be the base of the perpendicular from $C$ to $AB$ . Denote $\theta = \angle{CBH}.$ It is clear that $BG' = AG, CH = AF, \triangle CBH \ =\triangle ADF,$ the area of $ABCD$ is equal to the area of the rectangle $AFCH.$

The problem is reduced to finding $AH$ .

In triangle $ABC$ all altitudes are known: $AB : BC : AC = \frac{1}{CH}\ : \frac{1}{AE}\ : \frac{1}{BG'}\ =$ $= \frac{1}{AF}\ : \frac{1}{AE}\ : \frac{1}{AG}\ = 5 : 6 : 9.$ We apply the Law of Cosines to $\triangle ABC$ and get $:$ $\begin{align*} 2\cdot AB\cdot BC \cdot \cos\theta = AC^2 – AB^2 – BC^2, \end{align*}$ $\begin{align*} 2\cdot 5\cdot 6\cdot \cos\theta = 60 \cos\theta = 9^2 – 5^2 – 6^2 = 20, \cos\theta =\frac{1}{3}. \end{align*}$ $\begin{align*} BH = BC \cos\theta = \frac{BC}{3}.\end{align*}$ We apply the Pythagorean Law to $\triangle HBC$ and get $:$ $\begin{align*} HC^2 = 18^2 = BC^2 – BH^2 = 9\cdot BH^2 – BH^2 = 8 BH^2.\end{align*}$ $\begin{align*} BH = \frac{9}{\sqrt2}, AH = (\frac{5}{2} + 1)\cdot BH = \frac{63}{2\cdot \sqrt2}. \end{align*}$ Required area is $\begin{align*} K = \frac{63}{2\cdot \sqrt{2}} \cdot 18 = \frac{567}{\sqrt{2}} \implies \sqrt{2} K=\boxed{567}. \end{align*}$

vladimir.shelomovskii@gmail.com, vvsss

Solution 10 (Area)

Let $F$ be on $DC$ such that $AF \| DC$ . Let $G$ be on $BD$ such that $AG \| BD$ .

Let $m$ be the length of $AB$ . Let $n$ be the length of $AD$ .

The area of $\triangle ABD$ can be expressed in three ways: $\frac{1}{2}(15)(BC) = \frac{1}{2}(15)(n)$ , $\frac{1}{2}(18)(m)$ , and $\frac{1}{2}(10)(BD)$ .

$\frac{1}{2}(15)(n) = \frac{1}{2}(18)(m)$ $15n = 18m$ $5n = 6m$ $n = \frac{6}{5}m$

Now, $BD = BG + GD = \sqrt{m^2-100} + \sqrt{n^2-100}$ . We can substitute in $n = \frac{6}{5}m$ to get

$BD = \sqrt{m^2-100} + \sqrt{(\frac{6}{5}m)^2-100}$ .

We have $\frac{1}{2}(10)\left(\sqrt{m^2-100} + \sqrt{(\frac{6}{5}m)^2-100}\right) = \frac{1}{2}(18)(m)$ After a fairly straightforward algebraic bash, we get $m = \frac{45\sqrt{2}}{4}$ , and $n = (\frac{6}{5})(\frac{45\sqrt{2}}{4}) = \frac{27\sqrt{2}}{2}$ . By the Pythagorean Theorem on $\triangle ADF$ , $DF^2 = n^2 - 18^2 = \frac{729}{2} - 324 = \frac{81}{2}$ , and $DF = \frac{9\sqrt{2}}{2}$ .

Thus, $DC = 2DF + AB = 9\sqrt{2}+\frac{45\sqrt{2}}{4} = \frac{81\sqrt{2}}{4}$ . Therefore, $K = \frac{1}{2}(\frac{45\sqrt{2}}{4}+\frac{81\sqrt{2}}{4}) \cdot 18 = \frac{63\sqrt{2}}{2} \cdot 18 = \frac{567\sqrt{2}}{2}$ . The requested answer is $K \cdot \sqrt{2} = \boxed{567}$ .

~ adam_zheng

Video Solution

https://youtu.be/uItEKVj-tF8

~Mathproblemsolvingskills.com

Video Solution

https://www.youtube.com/watch?v=6rLnl8z7lnM

2021 AIME I (Problems • Answer Key • Resources)
Preceded by Problem 8	Followed by Problem 10
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search

Difference between revisions of "2021 AIME I Problems/Problem 9"

Latest revision as of 17:16, 25 January 2024

Contents

Problem

Diagram

Solution 1 (Similar Triangles and Pythagorean Theorem)

Solution 2 (Similar Triangles and Pythagorean Theorem)

Solution 3 (Similar Triangles and Pythagorean Theorem)

Solution 4 (Cyclic Quadrilaterals, Similar Triangles, Pythagorean Theorem)

Solution 5 (Cyclic Quadrilaterals, Similar Triangles, Pythagorean Theorem)

Solution 6 (Similar Triangles and Trigonometry)

Solution 7 (Similar Triangles and Trigonometry)

Solution 8 (Heron's Formula)

Solution 9 (Three Heights)

Solution 10 (Area)

Video Solution

Video Solution

See Also

@@ Line 2: / Line 2: @@
 Let <math>ABCD</math> be an isosceles trapezoid with <math>AD=BC</math> and <math>AB<CD.</math> Suppose that the distances from <math>A</math> to the lines <math>BC,CD,</math> and <math>BD</math> are <math>15,18,</math> and <math>10,</math> respectively. Let <math>K</math> be the area of <math>ABCD.</math> Find <math>\sqrt2 \cdot K.</math>
-==Solution 1==
+==Diagram==
-Construct your isosceles trapezoid. Let, for simplicity, <math>AB = a</math>, <math>AD = BC = b</math>, and <math>CD = c</math>. Extend the sides <math>BC</math> and <math>AD</math> mark the intersection as <math>P</math>. Following what the question states, drop a perpendicular from <math>A</math> to <math>BC</math> labeling the foot as <math>G</math>. Drop another perpendicular from <math>A</math> to <math>CD</math>, calling the foot <math>E</math>. Lastly, drop a perpendicular from <math>A</math> to <math>BD</math>, labeling it <math>F</math>. In addition, drop a perpendicular from <math>B</math> to <math>AC</math> calling its foot <math>F'</math>.
+<asy>
+/* Made by MRENTHUSIASM */
+size(250);
+pair A, B, C, D, E, F, G, H;
+A = (-45sqrt(2)/8,18);
+B = (45sqrt(2)/8,18);
+C = (81sqrt(2)/8,0);
+D = (-81sqrt(2)/8,0);
+E = foot(A,C,B);
+F = foot(A,C,D);
+G = foot(A,B,D);
+H = intersectionpoint(A--F,B--D);
+markscalefactor=0.1;
+draw(rightanglemark(A,E,B),red);
+draw(rightanglemark(A,F,C),red);
+draw(rightanglemark(A,G,D),red);
+dot("$A$",A,1.5*NW,linewidth(4));
+dot("$B$",B,1.5*NE,linewidth(4));
+dot("$C$",C,1.5*SE,linewidth(4));
+dot("$D$",D,1.5*SW,linewidth(4));
+dot(E,linewidth(4));
+dot(F,linewidth(4));
+dot(G,linewidth(4));
+draw(A--B--C--D--cycle^^B--D^^B--E);
+draw(A--E^^A--F^^A--G,dashed);
+label("$10$",midpoint(A--G),1.5*(1,0));
+label("$15$",midpoint(A--E),1.5*N);
+Label L = Label("$18$", align=(0,0), position=MidPoint, filltype=Fill(0,3,white));
+draw(C+(5,0)--(81sqrt(2)/8,18)+(5,0), L=L, arrow=Arrows(),bar=Bars(15));
+</asy>
+~MRENTHUSIASM
---DIAGRAM COMING SOON--
+==Solution 1 (Similar Triangles and Pythagorean Theorem)==
+Let <math>\overline{AE}, \overline{AF},</math> and <math>\overline{AG}</math> be the perpendiculars from <math>A</math> to <math>\overleftrightarrow{BC}, \overleftrightarrow{CD},</math> and <math>\overleftrightarrow{BD},</math> respectively. Next, let <math>H</math> be the intersection of <math>\overline{AF}</math> and <math>\overline{BD}.</math>
-Start out by constructing a triangle <math>ADH</math> congruent to <math>\triangle ABC</math> with its side of length <math>a</math> on line <math>DE</math>. This works because all isosceles triangles are cyclic and as a result, <math>\angle ADC + \angle ABC = 180^\circ</math>.
+We set <math>AB=x</math> and <math>AH=y,</math> as shown below.
+<asy>
+/* Made by MRENTHUSIASM */
+size(250);
+pair A, B, C, D, E, F, G, H;
+A = (-45sqrt(2)/8,18);
+B = (45sqrt(2)/8,18);
+C = (81sqrt(2)/8,0);
+D = (-81sqrt(2)/8,0);
+E = foot(A,C,B);
+F = foot(A,C,D);
+G = foot(A,B,D);
+H = intersectionpoint(A--F,B--D);
+markscalefactor=0.1;
+draw(rightanglemark(A,E,B),red);
+draw(rightanglemark(A,F,C),red);
+draw(rightanglemark(A,G,D),red);
+dot("$A$",A,1.5*NW,linewidth(4));
+dot("$B$",B,1.5*NE,linewidth(4));
+dot("$C$",C,1.5*SE,linewidth(4));
+dot("$D$",D,1.5*SW,linewidth(4));
+dot("$E$",E,1.5*dir(E),linewidth(4));
+dot("$F$",F,1.5*S,linewidth(4));
+dot("$G$",G,SE,linewidth(4));
+dot("$H$",H,SE,linewidth(4));
+draw(A--B--C--D--cycle^^B--D^^B--E);
+draw(A--E^^A--F^^A--G,dashed);
+label("$10$",midpoint(A--G),1.5*(1,0));
+label("$15$",midpoint(A--E),1.5*N);
+Label L = Label("$18$", align=(0,0), position=MidPoint, filltype=Fill(0,3,white));
+draw(C+(5,0)--(81sqrt(2)/8,18)+(5,0), L=L, arrow=Arrows(),bar=Bars(15));
+label("$x$",midpoint(A--B),N);
+label("$y$",midpoint(A--H),W);
+</asy>
+From here, we obtain <math>HF=18-y</math> by segment subtraction, and <math>BG=\sqrt{x^2-10^2}</math> and <math>HG=\sqrt{y^2-10^2}</math> by the Pythagorean Theorem.
-Notice that <math>\triangle AGC \sim \triangle BF'C</math> by AA similarity. We are given that <math>AG = 15</math> and by symmetry we can deduce that <math>F'B = 10</math>. As a result, <math>\frac{BF}{AG} = \frac{BC}{AC} = \frac{3}{2}</math>. This gives us that <math>AC = BD = \frac{3}{2} b</math>.
+Since <math>\angle ABG</math> and <math>\angle HAG</math> are both complementary to <math>\angle AHB,</math> we have <math>\angle ABG = \angle HAG,</math> from which <math>\triangle ABG \sim \triangle HAG</math> by AA. It follows that <math>\frac{BG}{AG}=\frac{AG}{HG},</math> so <math>BG\cdot HG=AG^2,</math> or <cmath>\sqrt{x^2-10^2}\cdot\sqrt{y^2-10^2}=10^2. \hspace{10mm} (1)</cmath>
+Since <math>\angle AHB = \angle FHD</math> by vertical angles, we have <math>\triangle AHB \sim \triangle FHD</math> by AA, with the ratio of similitude <math>\frac{AH}{FH}=\frac{BA}{DF}.</math> It follows that <math>DF=BA\cdot\frac{FH}{AH}=x\cdot\frac{18-y}{y}.</math>
-The question asks us along the lines of finding the area, <math>K</math>, of the trapezoid <math>ABCD</math>. We look at the area of <math>ABC</math> and notice that it can be represented as <math>\frac{1}{2} \cdot AC \cdot 10 = \frac{1}{2} \cdot a \cdot 18</math>. Substituting <math>AC = \frac{3}{2} b</math>, we solve for <math>a</math>, getting <math>a = \frac{5}{6} b</math>.
+Since <math>\angle EBA = \angle ECD = \angle FDA</math> by angle chasing, we have <math>\triangle EBA \sim \triangle FDA</math> by AA, with the ratio of similitude <math>\frac{EA}{FA}=\frac{BA}{DA}.</math> It follows that <math>DA=BA\cdot\frac{FA}{EA}=x\cdot\frac{18}{15}=\frac{6}{5}x.</math>
-Now let us focus on isosceles triangle <math>ACH</math>, where <math>AH = AC = \frac{3}{2} b</math>. Since, <math>AE</math> is an altitude from <math>A</math> to <math>CH</math> of an isosceles triangle, <math>HE</math> must be equal to <math>EC</math>. Since <math>DH = a</math> and <math>DC = c</math>, we can solve to get that <math>DE = \frac{c-a}{2}</math> and <math>EC = \frac{a+c}{2}</math>.
+By the Pythagorean Theorem on right <math>\triangle ADF,</math> we have <math>DF^2+AF^2=AD^2,</math> or <cmath>\left(x\cdot\frac{18-y}{y}\right)^2+18^2=\left(\frac{6}{5}x\right)^2. \hspace{7mm} (2)</cmath>
+Solving this system of equations (<math>(1)</math> and <math>(2)</math>), we get <math>x=\frac{45\sqrt2}{4}</math> and <math>y=\frac{90}{7},</math> so <math>AB=x=\frac{45\sqrt2}{4}</math> and <math>CD=AB+2DF=x+2\left(x\cdot\frac{18-y}{y}\right)=\frac{81\sqrt2}{4}.</math> Finally, the area of <math>ABCD</math> is <cmath>K=\frac{AB+CD}{2}\cdot AF=\frac{567\sqrt2}{2},</cmath> from which <math>\sqrt2 \cdot K=\boxed{567}.</math>
-We must then set up equations using the Pythagorean Theorem, writing everything in terms of <math>a</math>, <math>b</math>, and <math>c</math>. Looking at right triangle <math>AEC</math> we get <cmath>324 + \frac{(a + c)^2}{4} = \frac{9}{4} b^2</cmath> Looking at right triangle <math>AED</math> we get <cmath>b^2 - 324 = \frac{(c-a)^2}{4}</cmath> Now rearranging and solving, we get two equation <cmath>a+c = 3\sqrt{b^2 - 144}</cmath> <cmath>c - a = 2\sqrt{b^2 - 324}</cmath> Those are convenient equations as <math>c+a - (c-a) = 2a = \frac{5}{3} b</math> which gives us <cmath>3\sqrt{b^2 - 324} - 2\sqrt{b^2 - 324} = \frac{5}{3} b</cmath> After some "smart" calculation, we get that <math>b = \frac{27}{\sqrt{2}}</math>.
+~MRENTHUSIASM
-Notice that the question asks for <math>K\sqrt{2}</math>, and <math>K = \frac{1}{2} \cdot 18 \cdot (a+c)</math> by applying the trapezoid area formula. Fortunately, this is just <math>27\sqrt{b^2 - 144}</math>, and plugging in the value of <math>b = \frac{27}{\sqrt{2}}</math>, we get that <math>K\sqrt{2} = \boxed{567}</math>.
+<u><b>Remark</b></u>
-~Math_Genius_164
+Instead of solving the system of equations <math>(1)</math> and <math>(2),</math> which can be time consuming, by noting that <math>\triangle ACF \sim \triangle ABG</math> by AA, we could find out <math>\frac{AB}{AG} = \frac{AC}{AF}</math>, which gives <math>AC = \frac{9}{5}x</math>. We also know that <math>EB = \sqrt{x^2 - 15^2}</math> by Pythagorean Theorem on <math>\triangle ABE</math>. From <math>BC = AD = \frac{6}{5}x,</math> we apply the Pythagorean Theorem to <math>\triangle ACE</math> and obtain
-==Solution 2(LOC and Trig)==
+<cmath>AC^2 = (EB+BC)^2 + AE^2.</cmath>
-Call AD and BC <math>a</math>. Draw diagonal  AC and call the foot of the perpendicular from B to AC <math>G</math>. Call the foot of the perpendicular from A to line BC F, and call the foot of the perpindicular from A to DC H. Triangles CBG and CAF are similar, and we get that <math>\frac{10}{15}=\frac{a}{AC}</math> Therefore, <math>AC=1.5a</math>. It then follows that triangles ABF and ADH are similar. Using similar triangles, we can then find that <math>AB=\frac{5}{6}a</math>. Using the Law of Cosine on ABC, We can find that the cosine of angle ABC is <math>-\frac{1}{3}</math>. Since angles ABF and ADH are equivalent and supplementary to angle ABC, we know that the cosine of angle ADH is 1/3. It then follows that <math>a=\frac{27\sqrt{2}}{2}</math>. Then it can be found that the area <math>K</math> is <math>\frac{567\sqrt{2}}{2}</math>. Multiplying this by <math>\sqrt{2}</math>, the answer is <math>\boxed{567}</math>.
+Substituting, we get
--happykeeper
+<cmath>\frac{81}{25}x^2 = \left(\sqrt{x^2 -225}+\frac{6}{5}x\right)^2+225 \iff x = 3\sqrt{x^2 - 15^2},</cmath>
+from which <math>x = \frac{45\sqrt{2}}{4}.</math>
-==Solution 3 (Similarity)==
+~Chupdogs
-Let the foot of the altitude from A to BC be P, to CD be Q, and to BD be R.
-Note that all isosceles trapezoids are cyclic quadrilaterals; thus, <math>A</math> is on the circumcircle of <math>\triangle BCD</math> and we have that <math>PRQ</math> is the Simpson Line from <math>A</math>. As <math>\angle QAB = 90^\circ</math>, we have that <math>\angle QAR = 90^\circ - \angle RAB =\angle ABR = \angle APR = \angle APQ</math>, with the last equality coming from cyclic quadrilateral <math>APBR</math>. Thus, <math>\triangle QAR \sim \triangle QPA</math> and we have that <math>\frac{AQ}{AR} = \frac{PQ}{PA}</math> or that <math>\frac{18}{10} = \frac{QP}{15}</math>, which we can see gives us that <math>QP = 27</math>. Further ratios using the same similar triangles gives that <math>QR = \frac{25}{3}</math> and <math>RP = \frac{56}{3}</math>.
+==Solution 2 (Similar Triangles and Pythagorean Theorem)==
-We also see that quadrilaterals <math>APBR</math> and <math>ARDQ</math> are both cyclic, with diameters of the circumcircles being <math>AB</math> and <math>AQ</math> respectively. The intersection of the circumcircles are the points <math>A</math> and <math>R</math>, and we know <math>DRB</math> and <math>QRP</math> are both line segments passing through an intersection of the two circles with one endpoint on each circle. By Fact 5, we know then that there exists a spiral similarity with center A taking <math>\triangle APQ</math> to <math>\triangle APD</math>. Because we know a lot about <math>\triangle APQ</math> but very little about <math>\triangle APD</math> and we would like to know more, we wish to find the ratio of similitude between the two triangles.
+First, draw the diagram. Then, notice that since <math>ABCD</math> is isosceles, <math>\Delta ABD \cong \Delta BAC</math>, and the length of the altitude from <math>B</math> to <math>AC</math> is also <math>10</math>. Let the foot of this altitude be <math>F</math>, and let the foot of the altitude from <math>A</math> to <math>BC</math> be denoted as <math>E</math>. Then, <math>\Delta BCF \sim \Delta ACE</math>. So, <math>\frac{BC}{AC} = \frac{BF}{AE} = \frac{2}{3}</math>. Now, notice that <math>[ABC] = \frac{10 \cdot AC} {2} = \frac{AB \cdot 18}{2} \implies AC = \frac{9 \cdot AB}{5}</math>, where <math>[ABC]</math> denotes the area of triangle <math>ABC</math>. Letting <math>AB = x</math>, this equality becomes <math>AC = \frac{9x}{5}</math>. Also, from <math>\frac{BC}{AC} = \frac{2}{3}</math>, we have <math>BC = \frac{6x}{5}</math>. Now, by the Pythagorean theorem on triangles <math>ABF</math> and <math>CBF</math>, we have <math>AF = \sqrt{x^{2}-100}</math> and <math>CF = \sqrt{ \left( \frac{6x}{5} \right) ^{2}-100}</math>. Notice that <math>AC = AF + CF</math>, so <math>\frac{9x}{5} = \sqrt{x^{2}-100} + \sqrt{ \left( \frac{6x}{5} \right) ^{2}-100}</math>. Squaring both sides of the equation once, moving <math>x^{2}-100</math> and <math> \left( \frac{6x}{5} \right) ^{2}-100</math> to the right, dividing both sides by <math>2</math>, and squaring the equation once more, we are left with <math>\frac{32x^{4}}{25} = 324x^{2}</math>. Dividing both sides by <math>x^{2}</math> (since we know <math>x</math> is positive), we are left with <math>\frac{32x^{2}}{25} = 324</math>. Solving for <math>x</math> gives us <math>x = \frac{45}{2\sqrt{2}}</math>.
-To do this, we use the one number we have for <math>\triangle APD</math>: we know that the altitude from <math>A</math> to <math>BD</math> has length 10. As the two triangles are similar, if we can find the height from <math>A</math> to <math>PQ</math>, we can take the ratio of the two heights as the ratio of similitude. To do this, we once again note that <math>QP = 27</math>. Using this, we can drop the altitude from <math>A</math> to <math>QP</math> and let it intersect <math>QP</math> at <math>H</math>. Then, let <math>QH = x</math> and thus <math>HP=27-x</math>. We then have by the Pythagorean Theorem on <math>\triangle AQH</math> and <math>\triangle APH</math>: <cmath>15^2 - x^2 = 18^2 - (27-x)^2</cmath> <cmath>225 - x^2 = 324 - (x^2-54x+729)</cmath> <cmath>54x = 630</cmath> <cmath>x=\frac{35}{3}</cmath>
+Now, let the foot of the perpendicular from <math>A</math> to <math>CD</math> be <math>G</math>. Then let <math>DG = y</math>. Let the foot of the perpendicular from <math>B</math> to <math>CD</math> be <math>H</math>. Then, <math>CH</math> is also equal to <math>y</math>. Notice that <math>ABHG</math> is a rectangle, so <math>GH = x</math>. Now, we have <math>CG = GH + CH = x + y</math>. By the Pythagorean theorem applied to <math>\Delta AGC</math>, we have <math>(x+y)^{2}+18^{2}= \left( \frac{9x}{5} \right) ^{2}</math>. We know that <math>\frac{9x}{5} = \frac{9}{5} \cdot \frac{45}{2\sqrt{2}} = \frac{81}{2\sqrt{2}}</math>, so we can plug this into this equation. Solving for <math>x+y</math>, we get <math>x+y=\frac{63}{2\sqrt{2}}</math>.
-Then, <math>RH = QH - QR = \frac{35}{3} - \frac{25}{3} = \frac{10}{3}</math>. This gives us then from right triangle <math>\triangle ARH</math> that <math>AH = \frac{20\sqrt{2}}{3}</math> and thus the ratio of <math>\triangle APQ</math> to <math>\triangle ABD</math> is <math>\frac{3\sqrt{2}}{4}</math>. From this, we see then that <cmath>AB = AP * \frac{3\sqrt{2}}{4} = 15 * \frac{3\sqrt{2}}{4} = \frac{45\sqrt{2}}{4}</cmath> and <cmath>AD = AQ * \frac{3\sqrt{2}}{4} = 18 * \frac{3\sqrt{2}}{4} = \frac{27\sqrt{2}}{2}</cmath> The Pythagorean Theorem on <math>\triangle AQD</math> then gives that <cmath>QD = \sqrt{AD^2 - AQ^2} = \sqrt{(\frac{27\sqrt{2}}{2})^2 - 18^2} = \sqrt{\frac{81}{2}} = \frac{9\sqrt{2}}{2}</cmath>
+Finally, to find <math>[ABCD]</math>, we use the formula for the area of a trapezoid: <math>K = [ABCD] = \frac{b_{1}+b_{2}}{2} \cdot h = \frac{AB+CD}{2} \cdot 18 = \frac{x+(CG+DG)}{2} \cdot 18 = \frac{2x+2y}{2} \cdot 18 = (x+y) \cdot 18 = \frac{63}{2\sqrt{2}} \cdot 18 = \frac{567}{\sqrt{2}}</math>. The problem asks us for <math>K \cdot \sqrt{2}</math>, which comes out to be <math>\boxed{567}</math>.
-Then, we have the height of trapezoid <math>ABCD</math> is <math>AQ = 18</math>, the top base is <math>AB = \frac{45\sqrt{2}}{4}</math>, and the bottom base is <math>CD = \frac{45\sqrt{2}}{4} + 2*\frac{9\sqrt{2}}{2}</math>. From the equation of a trapezoid, <math>K = \frac{b_1+b_2}{2} h = \frac{63\sqrt{2}}{4} * 18 = \frac{567\sqrt{2}}{2}</math>, so the answer is <math>K\sqrt{2} = \boxed{567}</math>.
+~advanture
-- lvmath
+==Solution 3 (Similar Triangles and Pythagorean Theorem)==
+Make <math>AE</math> perpendicular to <math>BC</math>; <math>AG</math> perpendicular to <math>BD</math>; <math>AF</math> perpendicular <math>DC</math>.
-==See also==
+It's obvious that <math>\triangle{AEB} \sim \triangle{AFD}</math>. Let <math>EB=5x; AB=5y; DF=6x; AD=6y</math>. Then make <math>BQ</math> perpendicular to <math>DC</math>, it's easy to get <math>BQ=18</math>.
+Since <math>AB</math> parallel to <math>DC</math>, <math>\angle{ABG}=\angle{BDQ}</math>, so <math>\triangle{ABG} \sim \triangle{BDQ}</math>. After drawing the altitude, it's obvious that <math>FQ=AB=5y</math>, so <math>DQ=5y+6x</math>. According to the property of similar triangles, <math>AG/BQ=BG/DQ</math>. So, <math>\frac{5}{9}=\frac{GB}{(6x+5y)}</math>, or <math>GB=\frac{(30x+25y)}{9}</math>.
+Now, we see the <math>\triangle AEB</math>, pretty easy to find that <math>15^2+(5x)^2=(5y)^2</math>, then we get <math>x^2+9=y^2</math>, then express <math>y</math> into <math>x</math> form that <math>y=\sqrt{x^2+9}</math>
+we put the length of <math>BG</math> back to <math>\triangle AGB</math>: <math>BG^2+100=AB^2</math>. So, <cmath>\frac{[30x+25\sqrt{(x^2+9)}]^2}{81}+100=(5\sqrt{x^2+9})^2.</cmath>
+After calculating, we can have a final equation of <math>x^2+9=\sqrt{x^2+9}\cdot3x</math>. It's easy to find <math>x=\frac{3\sqrt{2}}{4}</math> then <math>y=\frac{9\sqrt{2}}{4}</math>. So, <cmath>\sqrt{2}\cdot K = \sqrt{2}\cdot(5y+5y+6x+6x)\cdot9=\boxed{567}.</cmath>
+~bluesoul
+==Solution 4 (Cyclic Quadrilaterals, Similar Triangles, Pythagorean Theorem)==
+Let the foot of the altitude from <math>A</math> to <math>BC</math> be <math>P</math>, to <math>CD</math> be <math>Q</math>, and to <math>BD</math> be <math>R</math>.
+Note that all isosceles trapezoids are cyclic quadrilaterals; thus, <math>A</math> is on the circumcircle of <math>\triangle BCD</math> and we have that <math>PRQ</math> is the Simson Line from <math>A</math>. As <math>\angle QAB = 90^\circ</math>, we have that <math>\angle QAR = 90^\circ - \angle RAB =\angle ABR = \angle APR = \angle APQ</math>, with the last equality coming from cyclic quadrilateral <math>APBR</math>. Thus, <math>\triangle QAR \sim \triangle QPA</math> and we have that <math>\frac{AQ}{AR} = \frac{PQ}{PA}</math> or that <math>\frac{18}{10} = \frac{QP}{15}</math>, which we can see gives us that <math>QP = 27</math>. Further ratios using the same similar triangles gives that <math>QR = \frac{25}{3}</math> and <math>RP = \frac{56}{3}</math>.
+We also see that quadrilaterals <math>APBR</math> and <math>ARQD</math> are both cyclic, with diameters of the circumcircles being <math>AB</math> and <math>AD</math> respectively. The intersection of the circumcircles are the points <math>A</math> and <math>R</math>, and we know <math>DRB</math> and <math>QRP</math> are both line segments passing through an intersection of the two circles with one endpoint on each circle. By Fact 5, we know then that there exists a spiral similarity with center <math>A</math> taking <math>\triangle APQ</math> to <math>\triangle APD</math>. Because we know a lot about <math>\triangle APQ</math> but very little about <math>\triangle APD</math> and we would like to know more, we wish to find the ratio of similitude between the two triangles.
+To do this, we use the one number we have for <math>\triangle APD</math>: we know that the altitude from <math>A</math> to <math>BD</math> has length <math>10</math>. As the two triangles are similar, if we can find the height from <math>A</math> to <math>PQ</math>, we can take the ratio of the two heights as the ratio of similitude. To do this, we once again note that <math>QP = 27</math>. Using this, we can drop the altitude from <math>A</math> to <math>QP</math> and let it intersect <math>QP</math> at <math>H</math>. Then, let <math>QH = x</math> and thus <math>HP=27-x</math>. We then have by the Pythagorean Theorem on <math>\triangle AQH</math> and <math>\triangle APH</math>:
+<cmath>\begin{align*}
+^2 - x^2 &= 18^2 - (27-x)^2 \\
+- x^2 &= 324 - (x^2-54x+729) \\
+x &= 630 \\
+x &= \frac{35}{3}.
+\end{align*}</cmath>
+Then, <math>RH = QH - QR = \frac{35}{3} - \frac{25}{3} = \frac{10}{3}</math>. This gives us then from right triangle <math>\triangle ARH</math> that <math>AH = \frac{20\sqrt{2}}{3}</math> and thus the ratio of <math>\triangle APQ</math> to <math>\triangle ABD</math> is <math>\frac{3\sqrt{2}}{4}</math>. From this, we see then that <cmath>AB = AP \cdot \frac{3\sqrt{2}}{4} = 15 \cdot \frac{3\sqrt{2}}{4} = \frac{45\sqrt{2}}{4}</cmath> and <cmath>AD = AQ \cdot \frac{3\sqrt{2}}{4} = 18 \cdot \frac{3\sqrt{2}}{4} = \frac{27\sqrt{2}}{2}.</cmath> The Pythagorean Theorem on <math>\triangle AQD</math> then gives that <cmath>QD = \sqrt{AD^2 - AQ^2} = \sqrt{\left(\frac{27\sqrt{2}}{2}\right)^2 - 18^2} = \sqrt{\frac{81}{2}} = \frac{9\sqrt{2}}{2}.</cmath>
+Then, we have the height of trapezoid <math>ABCD</math> is <math>AQ = 18</math>, the top base is <math>AB = \frac{45\sqrt{2}}{4}</math>, and the bottom base is <math>CD = \frac{45\sqrt{2}}{4} + 2\cdot\frac{9\sqrt{2}}{2}</math>. From the equation of a trapezoid, <math>K = \frac{b_1+b_2}{2} \cdot h = \frac{63\sqrt{2}}{4} \cdot 18 = \frac{567\sqrt{2}}{2}</math>, so the answer is <math>K\sqrt{2} = \boxed{567}</math>.
+~lvmath
+==Solution 5 (Cyclic Quadrilaterals, Similar Triangles, Pythagorean Theorem)==
+Let <math>E,F,</math> and <math>G</math> be the feet of the altitudes from <math>A</math> to <math>BC,CD,</math> and <math>DB</math>, respectively.
+Claim: We have <math>2</math> pairs of similar right triangles: <math>\triangle AEB \sim \triangle AFD</math> and <math>\triangle AGD \sim \triangle AEC</math>.
+Proof: Note that <math>ABCD</math> is cyclic. We need one more angle, and we get this from this cyclic quadrilateral:
+<cmath>\begin{align*}
+\angle ABE &= 180^\circ - \angle ABC =\angle ADC = \angle ADG, \\
+\angle ADG &= \angle ADB =\angle ACB = \angle ACE. \hspace{20mm} \square
+\end{align*}</cmath>
+Let <math>AD=a</math>. We obtain from the similarities <math>AB = \frac{5a}{6}</math> and <math>AC=BD=\frac{3a}{2}</math>.
+By Ptolemy, <math>\left(\frac{3a}{2}\right)^2 = a^2 + \frac{5a}{6} \cdot CD</math>, so <math>\frac{5a^2}{4} = \frac{5a}{6} \cdot CD</math>.
+We obtain <math>CD=\frac{3a}{2}</math>, so <math>DF=\frac{CD-AB}{2}=\frac{a}{3}</math>.
+Applying the Pythagorean theorem on <math>\triangle ADF</math>, we get <math>324=a^2 - \frac{a^2}{9}=\frac{8a^2}{9}</math>.
+Thus, <math>a=\frac{27}{\sqrt{2}}</math>, and <math>[ABCD]=\frac{AB+CD}{2} \cdot 18 = \frac{\frac{5a}{6} +\frac{9a}{6}}{2} \cdot 18 = 18 \cdot \frac{7}{6} \cdot \frac{27}{\sqrt{2}} = \frac{567}{\sqrt{2}}</math>, yielding <math>\sqrt2\cdot[ABCD]=\boxed{567}</math>.
+==Solution 6 (Similar Triangles and Trigonometry)==
+Let <math>AD=BC=a</math>. Draw diagonal <math>AC</math> and let <math>G</math> be the foot of the perpendicular from <math>B</math> to <math>AC</math>, <math>F</math> be the foot of the perpendicular from <math>A</math> to line <math>BC</math>, and <math>H</math> be the foot of the perpendicular from <math>A</math> to <math>DC</math>.
+Note that <math>\triangle CBG\sim\triangle CAF</math>, and we get that <math>\frac{10}{15}=\frac{a}{AC}</math>. Therefore, <math>AC=\frac32 a</math>. It then follows that <math>\triangle ABF\sim\triangle ADH</math>. Using similar triangles, we can then find that <math>AB=\frac{5}{6}a</math>. Using the Law of Cosines on <math>\triangle ABC</math>, We can find that the <math>\cos\angle ABC=-\frac{1}{3}</math>. Since <math>\angle ABF=\angle ADH</math>, and each is supplementary to <math>\angle ABC</math>, we know that the <math>\cos\angle ADH=\frac{1}{3}</math>. It then follows that <math>a=\frac{27\sqrt{2}}{2}</math>. Then it can be found that the area <math>K</math> is <math>\frac{567\sqrt{2}}{2}</math>. Multiplying this by <math>\sqrt{2}</math>, the answer is <math>\boxed{567}</math>.
+~happykeeper
+==Solution 7 (Similar Triangles and Trigonometry)==
+Draw the distances in terms of <math>B</math>, as shown in the diagram. By similar triangles, <math>\triangle{AEC}\sim\triangle{BIC}</math>. As a result, let <math>AB=u</math>, then <math>BC=AD=\frac{6}{5}u</math> and <math>2AC=3BC</math>. The triangle <math>ABC</math> is <math>6-5-9</math> which <math>\cos(\angle{ABC})=-\frac{1}{3}</math>. By angle subtraction, <math>\cos(180-\theta)=-\cos\theta</math>. Therefore, <math>AB=\frac{45}{2\sqrt{2}}=\frac{45\sqrt{2}}{4}</math> and <math>AD=BC=\frac{27}{\sqrt{2}}</math>. By trapezoid area formula, the area of <math>ABCD</math> is equal to <math>(AB+DF)\cdot 18=567\cdot \frac{\sqrt{2}}{2}</math> which <math>\sqrt{2}\cdot k=\boxed{567}</math>.
+~math2718281828459
+==Solution 8 (Heron's Formula)==
+<asy>
+size(250);
+pair A, B, C, D, E, F, G, H;
+A = (-45sqrt(2)/8,18);
+B = (45sqrt(2)/8,18);
+C = (81sqrt(2)/8,0);
+D = (-81sqrt(2)/8,0);
+E = foot(A,C,B);
+F = foot(A,C,D);
+G = foot(A,B,D);
+H = intersectionpoint(A--F,B--D);
+markscalefactor=0.1;
+draw(rightanglemark(A,E,B),red);
+draw(rightanglemark(A,F,C),red);
+draw(rightanglemark(A,G,D),red);
+filldraw(A--D--F--cycle,yellow,black+linewidth(1.5));
+filldraw(A--B--E--cycle,yellow,black+linewidth(1.5));
+dot("$A$",A,1.5*NW,linewidth(4));
+dot("$B$",B,1.5*NE,linewidth(4));
+dot("$C$",C,1.5*SE,linewidth(4));
+dot("$D$",D,1.5*SW,linewidth(4));
+dot(E,linewidth(4));
+dot(F,linewidth(4));
+dot(G,linewidth(4));
+label("$E$",E,NE);
+label("$F$",F, S);
+label("$G$",G,SE);
+draw(A--B--C--D--cycle^^B--D^^B--E);
+draw(A--E^^A--F^^A--G,dashed);
+label("$10$",midpoint(A--G),1.5*(1,0));
+label("$15$",midpoint(A--E),1.5*N);
+label("$5x$",midpoint(A--B),S);
+label("$6x$",midpoint(A--D),1.5*(-1,0));
+Label L = Label("$18$", align=(0,0), position=MidPoint, filltype=Fill(0,3,white));
+draw(C+(5,0)--(81sqrt(2)/8,18)+(5,0), L=L, arrow=Arrows(),bar=Bars(15));
+</asy>
+Let the points formed by dropping altitudes from <math>A</math> to the lines <math>BC</math>, <math>CD</math>, and <math>BD</math> be <math>E</math>, <math>F</math>, and <math>G</math>, respectively.
+We have
+<cmath>\triangle ABE \sim \triangle ADF \implies \frac{AD}{18} = \frac{AB}{15} \implies AD = \frac{6}{5}AB</cmath>
+and
+<cmath>BD\cdot10 = 2[ABD] = AB\cdot18 \implies BD = \frac{9}{5}AB.</cmath>
+For convenience, let <math>AB = 5x</math>. By Heron's formula on <math>\triangle ABD</math>, we have sides <math>5x,6x,9x</math> and semiperimeter <math>10x</math>, so
+<cmath>\sqrt{10x\cdot5x\cdot4x\cdot1x} = [ABD] = \frac{AB\cdot18}{2} = 45x \implies 10\sqrt{2}x^2 = 45x \implies x= \frac{45}{10\sqrt{2}},</cmath>
+so <math>AB = 5x = \frac{45}{2\sqrt{2}}</math>.
+Then,
+<cmath>BE = \sqrt{AB^2 - CA^2} = \sqrt{\left(\frac{45}{2\sqrt{2}}\right)^2 - 15^2} = \sqrt{\frac{225}{8}} = \frac{15}{2\sqrt{2}}</cmath>
+and
+<cmath>\triangle ABE \sim \triangle ADF \implies DF = \frac{6}{5}BE = \frac{6}{5}\cdot\frac{15}{2\sqrt{2}} = \frac{18}{2\sqrt{2}}.</cmath>
+Finally, recalling that <math>ABCD</math> is isosceles,
+<cmath>K = [ABCD] = \frac{18}{2}(AB + (AB + 2DF)) = 18(AB + DF) = 18\left(\frac{45}{2\sqrt{2}} + \frac{18}{2\sqrt{2}}\right) = \frac{567}{\sqrt{2}},</cmath>
+so <math>\sqrt{2}\cdot K = \boxed{567}</math>.
+~[[User:emerald_block|emerald_block]]
+==Solution 9 (Three Heights)==
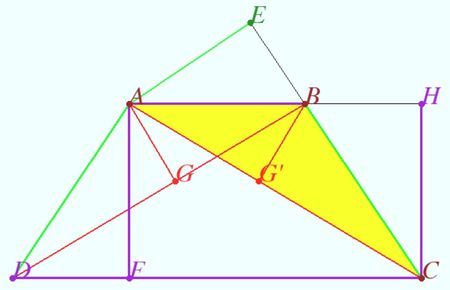
+[[File:2021 AIME I 9.jpg|450px|right]]
+Let <math>\overline{AE}, \overline{AF},</math> and <math>\overline{AG}</math> be the perpendiculars from <math>A</math> to <math>{BC}, {CD},</math> and <math>{BD},</math> respectively.
+<math>AE = 15, AF = 18, AG =10</math>.
+Denote by <math>G'</math> the base of the perpendicular from <math>B</math> to <math>AC, H</math> be the base of the perpendicular from <math>C</math> to <math>AB</math>. Denote <math>\theta = \angle{CBH}.</math>
+It is clear that <cmath>BG' = AG, CH = AF, \triangle CBH \ =\triangle ADF,</cmath> the area of <math>ABCD</math>  is equal to the area of the rectangle   <math>AFCH.</math>
+The problem is reduced to finding <math>AH</math>.
+In triangle <math>ABC</math> all altitudes are known:
+<cmath>AB : BC : AC =  \frac{1}{CH}\ : \frac{1}{AE}\ : \frac{1}{BG'}\ =</cmath>
+<cmath>= \frac{1}{AF}\ :  \frac{1}{AE}\ :  \frac{1}{AG}\ = 5 : 6 : 9.</cmath>
+We apply the Law of Cosines to <math>\triangle ABC</math> and get<math>:</math>
+<cmath>\begin{align*} 2\cdot AB\cdot BC \cdot \cos\theta = AC^2 – AB^2 – BC^2, \end{align*}</cmath>
+<cmath>\begin{align*} 2\cdot 5\cdot 6\cdot \cos\theta  = 60 \cos\theta  = 9^2 – 5^2 – 6^2 = 20, \cos\theta  =\frac{1}{3}. \end{align*}</cmath>
+<cmath>\begin{align*} BH = BC \cos\theta = \frac{BC}{3}.\end{align*}</cmath>
+We apply the Pythagorean Law to <math>\triangle HBC</math> and get<math>:</math>
+<cmath>\begin{align*} HC^2 = 18^2 = BC^2 – BH^2 = 9\cdot BH^2 – BH^2 = 8 BH^2.\end{align*}</cmath>
+<cmath>\begin{align*} BH =  \frac{9}{\sqrt2}, AH = (\frac{5}{2} + 1)\cdot BH =  \frac{63}{2\cdot \sqrt2}. \end{align*}</cmath>
+Required area is
+<cmath>\begin{align*}  K =  \frac{63}{2\cdot \sqrt{2}} \cdot 18 =  \frac{567}{\sqrt{2}} \implies \sqrt{2} K=\boxed{567}. \end{align*}</cmath>
+'''vladimir.shelomovskii@gmail.com, vvsss'''
+==Solution 10 (Area)==
+Let <math>F</math> be on <math>DC</math> such that <math>AF \| DC</math>. Let <math>G</math> be on <math>BD</math> such that <math>AG \| BD</math>.
+Let <math>m</math> be the length of <math>AB</math>. Let <math>n</math> be the length of <math>AD</math>.
+The area of <math>\triangle ABD</math> can be expressed in three ways: <math>\frac{1}{2}(15)(BC) = \frac{1}{2}(15)(n)</math>, <math>\frac{1}{2}(18)(m)</math>, and <math>\frac{1}{2}(10)(BD)</math>.
+<cmath>
+\frac{1}{2}(15)(n) = \frac{1}{2}(18)(m)
+</cmath>
+<cmath>
+n = 18m
+</cmath>
+<cmath>
+n = 6m
+</cmath>
+<cmath>
+n = \frac{6}{5}m
+</cmath>
+Now, <math>BD = BG + GD = \sqrt{m^2-100} + \sqrt{n^2-100}</math>. We can substitute in <math>n = \frac{6}{5}m</math> to get
+<math>BD = \sqrt{m^2-100} + \sqrt{(\frac{6}{5}m)^2-100}</math>.
+We have
+<cmath>
+\frac{1}{2}(10)\left(\sqrt{m^2-100} + \sqrt{(\frac{6}{5}m)^2-100}\right) = \frac{1}{2}(18)(m)
+</cmath>
+After a fairly straightforward algebraic bash, we get <math>m = \frac{45\sqrt{2}}{4}</math>, and <math>n = (\frac{6}{5})(\frac{45\sqrt{2}}{4}) = \frac{27\sqrt{2}}{2}</math>. By the Pythagorean Theorem on <math>\triangle ADF</math>, <math>DF^2 = n^2 - 18^2 = \frac{729}{2} - 324 = \frac{81}{2}</math>, and <math>DF = \frac{9\sqrt{2}}{2}</math>.
+Thus, <math>DC = 2DF + AB = 9\sqrt{2}+\frac{45\sqrt{2}}{4} = \frac{81\sqrt{2}}{4}</math>. Therefore, <math>K = \frac{1}{2}(\frac{45\sqrt{2}}{4}+\frac{81\sqrt{2}}{4}) \cdot 18 = \frac{63\sqrt{2}}{2} \cdot 18 = \frac{567\sqrt{2}}{2}</math>. The requested answer is <math>K \cdot \sqrt{2} = \boxed{567}</math>.
+~ adam_zheng
+==Video Solution==
+https://youtu.be/uItEKVj-tF8
+~Mathproblemsolvingskills.com
+==Video Solution==
+https://www.youtube.com/watch?v=6rLnl8z7lnM
+==See Also==
 {{AIME box|year=2021|n=I|num-b=8|num-a=10}}
 [[Category:Intermediate Geometry Problems]]
 {{MAA Notice}}