Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2021 AMC 10A Problems/Problem 24"

m (→‎Solution 2.2 (Shoelace Formula))
(→‎Solution 1 (Generalized Value of a))
 
(83 intermediate revisions by 5 users not shown)
Line 1: Line 1:
 
==Problem==
 
==Problem==
−
The interior of a quadrilateral is bounded by the graphs of <math>(x+ay)^2 = 4a^2</math> and <math>(ax-y)^2 = a^2</math>, where <math>a</math> a positive real number. What is the area of this region in terms of <math>a</math>, valid for all <math>a > 0</math>?
+
The interior of a quadrilateral is bounded by the graphs of <math>(x+ay)^2 = 4a^2</math> and <math>(ax-y)^2 = a^2</math>, where <math>a</math> is a positive real number. What is the area of this region in terms of <math>a</math>, valid for all <math>a > 0</math>?
  
 
<math>\textbf{(A)} ~\frac{8a^2}{(a+1)^2}\qquad\textbf{(B)} ~\frac{4a}{a+1}\qquad\textbf{(C)} ~\frac{8a}{a+1}\qquad\textbf{(D)} ~\frac{8a^2}{a^2+1}\qquad\textbf{(E)} ~\frac{8a}{a^2+1}</math>
 
<math>\textbf{(A)} ~\frac{8a^2}{(a+1)^2}\qquad\textbf{(B)} ~\frac{4a}{a+1}\qquad\textbf{(C)} ~\frac{8a}{a+1}\qquad\textbf{(D)} ~\frac{8a^2}{a^2+1}\qquad\textbf{(E)} ~\frac{8a}{a^2+1}</math>
  
−
==Solution 1==
+
==Diagram==
−
The conditions <math>(x+ay)^2 = 4a^2</math> and <math>(ax-y)^2 = a^2</math> give <math>|x+ay| = |2a|</math> and <math>|ax-y| = |a|</math> or <math>x+ay = \pm 2a</math> and <math>ax-y = \pm a</math>. The slopes here are perpendicular, so the quadrilateral is a rectangle.
+
Graph in Desmos: https://www.desmos.com/calculator/satawguqsc
−
Plug in <math>a=1</math> and graph it. We quickly see that the area is <math>2\sqrt{2} \cdot \sqrt{2} = 4</math>, so the answer can't be <math>A</math> or <math>B</math> by testing the values they give (test it!). Now plug in <math>a=2</math>. We see using a ruler that the sides of the rectangle are about <math>\frac74</math> and <math>\frac72</math>. So the area is about <math>\frac{49}8 = 6.125</math>. Testing <math>C</math> we get <math>\frac{16}3</math> which is clearly less than <math>6</math>, so it is out. Testing <math>D</math> we get <math>\frac{32}5</math> which is near our answer, so we leave it. Testing <math>E</math> we get <math>\frac{16}5</math>, way less than <math>6</math>, so it is out. So, the only plausible answer is <math>\boxed{D}</math> ~firebolt360
+
 
 +
~MRENTHUSIASM
 +
 
 +
==Solution 1 (Generalized Value of a)==
 +
The cases for <math>(x+ay)^2 = 4a^2</math> are <math>x+ay = \pm2a,</math> or two parallel lines. We rearrange each case and construct the table below:
 +
<cmath>\begin{array}{c||c|c|c|c}
 +
& & & & \\ [-2.5ex]
 +
\textbf{Case} & \textbf{Line's Equation} & \boldsymbol{x}\textbf{-Intercept} & \boldsymbol{y}\textbf{-Intercept} & \textbf{Slope} \\ [0.5ex]
 +
\hline
 +
& & & & \\ [-1.5ex]
 +
1 & x+ay-2a=0 & 2a & 2 & -\frac1a  \\ [2ex]
 +
2 & x+ay+2a=0 & -2a & -2 & -\frac1a \\ [0.75ex]
 +
\end{array}</cmath>
 +
The cases for <math>(ax-y)^2 = a^2</math> are <math>ax-y=\pm a,</math> or two parallel lines. We rearrange each case and construct the table below:
 +
<cmath>\begin{array}{c||c|c|c|c}
 +
& & & & \\ [-2.5ex]
 +
\textbf{Case} & \textbf{Line's Equation} & \boldsymbol{x}\textbf{-Intercept} & \boldsymbol{y}\textbf{-Intercept} & \textbf{Slope} \\ [0.5ex]
 +
\hline
 +
& & & & \\ [-1.5ex]
 +
1* & ax-y-a=0 & 1 & -a & a  \\ [2ex]
 +
2* & ax-y+a=0 & -1 & a & a \\ [0.75ex]
 +
\end{array}</cmath>
 +
Since the slopes of intersecting lines <math>(1)\cap(1*), (1)\cap(2*), (2)\cap(1*),</math> and <math>(2)\cap(2*)</math> are negative reciprocals, we get four right angles, from which the quadrilateral is a rectangle.
 +
 
 +
Two solutions follow from here:
 +
 
 +
===Solution 1.1 (Distance Between Parallel Lines)===
 +
Recall that for constants <math>A,B,C_1</math> and <math>C_2,</math> the distance <math>d</math> between parallel lines
 +
<math>\begin{cases}
 +
Ax+By+C_1=0 \\
 +
Ax+By+C_2=0
 +
\end{cases}</math> is <cmath>d=\frac{\left|C_2-C_1\right|}{\sqrt{A^2+B^2}}.</cmath>
 +
From this formula:
 +
 
 +
* The distance between lines <math>(1)</math> and <math>(2)</math> is <math>\frac{4a}{\sqrt{1+a^2}},</math> the length of this rectangle.
  
−
==Solution 2 (Casework)==
+
* The distance between lines <math>(1*)</math> and <math>(2*)</math> is <math>\frac{2a}{\sqrt{a^2+1}},</math> the width of this rectangle.
−
For the equation <math>(x+ay)^2 = 4a^2,</math> the cases are
 
  
−
<math>(1) \ x+ay=2a.</math> This is a line with <math>x</math>-intercept <math>2a,y</math>-intercept <math>2,</math> and slope <math>-\frac 1a.</math>
+
The area we seek is <cmath>\frac{4a}{\sqrt{1+a^2}}\cdot\frac{2a}{\sqrt{a^2+1}}=\boxed{\textbf{(D)} ~\frac{8a^2}{a^2+1}}.</cmath>
 +
~MRENTHUSIASM
  
−
<math>(2) \ x+ay=-2a.</math> This is a line with <math>x</math>-intercept <math>-2a,y</math>-intercept <math>-2,</math> and slope <math>-\frac 1a.</math>
+
===Solution 1.2 (Distance Between Points)===
 +
The solutions to systems of equations <math>(1)\cap(1*), (1)\cap(2*), (2)\cap(2*), (2)\cap(1*)</math> are <cmath>(x,y)=\left(\frac{a(a+2)}{a^2+1},\frac{a(2a-1)}{a^2+1}\right), \left(-\frac{a(a-2)}{a^2+1},\frac{a(2a+1)}{a^2+1}\right), \left(-\frac{a(a+2)}{a^2+1},-\frac{a(2a-1)}{a^2+1}\right), \left(\frac{a(a-2)}{a^2+1},-\frac{a(2a+1)}{a^2+1}\right),</cmath> respectively, which are the consecutive vertices of this rectangle.
  
−
For the equation <math>(ax-y)^2 = a^2,</math> the cases are
+
By the Distance Formula, the length and width of this rectangle are <math>\frac{4a\sqrt{a^2+1}}{a^2+1}</math> and <math>\frac{2a\sqrt{a^2+1}}{a^2+1},</math> respectively.
  
−
<math>(1') \ ax-y=a.</math> This is a line with <math>x</math>-intercept <math>1,y</math>-intercept <math>-a,</math> and slope <math>a.</math>
+
The area we seek is <cmath>\frac{4a\sqrt{a^2+1}}{a^2+1}\cdot\frac{2a\sqrt{a^2+1}}{a^2+1}=\boxed{\textbf{(D)} ~\frac{8a^2}{a^2+1}}.</cmath>
 +
~MRENTHUSIASM
  
−
<math>(2') \ ax-y=-a.</math> This is a line with <math>x</math>-intercept <math>-1,y</math>-intercept <math>a,</math> and slope <math>a.</math>
+
==Solution 2 (Specified Value of a)==
 +
In this solution, we will refer to equations <math>(1),(2),(1*),</math> and <math>(2*)</math> from Solution 1.
  
−
Plugging <math>a=2</math> into the choices gives  
+
Substituting <math>a=2</math> into the answer choices gives  
  
 
<math>\textbf{(A)} ~\frac{32}{9}\qquad\textbf{(B)} ~\frac{8}{3}\qquad\textbf{(C)} ~\frac{16}{3}\qquad\textbf{(D)} ~\frac{32}{5}\qquad\textbf{(E)} ~\frac{16}{5}</math>
 
<math>\textbf{(A)} ~\frac{32}{9}\qquad\textbf{(B)} ~\frac{8}{3}\qquad\textbf{(C)} ~\frac{16}{3}\qquad\textbf{(D)} ~\frac{32}{5}\qquad\textbf{(E)} ~\frac{16}{5}</math>
  
−
Plugging <math>a=2</math> into the four above equations and solving systems of equations for intersecting lines [<math>(1)</math> and <math>(1'), (1)</math> and <math>(2'), (2)</math> and <math>(1'), (2)</math> and <math>(2')</math>], we get the respective solutions <cmath>(x,y)=\left(\frac 85, \frac 65\right), (0,2), \left(-\frac 85, -\frac 65\right), (0,-2).</cmath>  
+
At <math>a=2,</math> the solutions to systems of equations <math>(1)\cap(1*), (1)\cap(2*), (2)\cap(2*), (2)\cap(1*)</math> are <cmath>(x,y)=\left(\frac 85, \frac 65\right), (0,2), \left(-\frac 85, -\frac 65\right), (0,-2),</cmath> respectively, which are the consecutive vertices of the quadrilateral.
−
===Solution 2.1 (Rectangle)===
+
 
−
Since the slopes of the intersecting lines (from the four above equations) are negative reciprocals, the quadrilateral is a rectangle. Finally, by the Distance Formula, the length and width of the rectangle are <math>\frac{8\sqrt5}{5}</math> and <math>\frac{4\sqrt5}{5}.</math> The area we seek is <cmath>\left(\frac{8\sqrt5}{5}\right)\left(\frac{4\sqrt5}{5}\right)=\frac{32}{5}.</cmath>
+
Two solutions follow from here:
 +
 
 +
===Solution 2.1 (Area of a Rectangle)===
 +
From the tables in Solution 1, we conclude that the quadrilateral is a rectangle.
 +
 
 +
By the Distance Formula, the length and width of this rectangle are <math>\frac{8\sqrt5}{5}</math> and <math>\frac{4\sqrt5}{5},</math> respectively.
  
−
The answer is <math>\boxed{\textbf{(D)} ~\frac{8a^2}{a^2+1}}.</math>
+
The area we seek is <cmath>\frac{8\sqrt5}{5}\cdot\frac{4\sqrt5}{5}=\frac{32}{5},</cmath> from which the answer is <math>\boxed{\textbf{(D)} ~\frac{8a^2}{a^2+1}}.</math>
  
 
~MRENTHUSIASM
 
~MRENTHUSIASM
  
−
===Solution 2.2 (Shoelace Formula)===
+
===Solution 2.2 (Area of a General Quadrilateral)===
−
Even if we do not recognize that the solutions form the vertices of a rectangle, we can apply the Shoelace Formula on <b><u>consecutive</u></b> vertices  
+
Even if we do not recognize that the quadrilateral is a rectangle, we can apply the Shoelace Theorem to its <i><b>consecutive</b></i> vertices
 
<cmath>\begin{align*}
 
<cmath>\begin{align*}
−
(x_1,y_1) &= \left(\frac 85, \frac 65\right), \\
+
(x_1,y_1) &= \left(\frac 85, \frac 65\right), \\  
−
(x_2,y_2) &= (0,2), \\
+
(x_2,y_2) &= (0,2), \\  
−
(x_3,y_3) &= \left(-\frac 85, -\frac 65\right), \\
+
(x_3,y_3) &= \left(-\frac 85, -\frac 65\right), \\  
 
(x_4,y_4) &= (0,-2).
 
(x_4,y_4) &= (0,-2).
 
\end{align*}</cmath>
 
\end{align*}</cmath>
 +
The area we seek is <cmath>\frac{1}{2} \left|(x_1y_2 + x_2y_3 + x_3y_4 + x_4y_1) - (y_1x_2 + y_2x_3 + y_3x_4 + y_4x_1)\right| = \frac{32}{5}.</cmath> from which the answer is <math>\boxed{\textbf{(D)} ~\frac{8a^2}{a^2+1}}.</math>
  
−
The area formula is
+
~MRENTHUSIASM
−
<cmath>\begin{align*}
 
−
A &= \frac{1}{2} \left|(x_1y_2 + x_2y_3 + x_3y_4 + x_4y_1) - (y_1x_2 + y_2x_3 + y_3x_4 + y_4x_1)\right| \\
 
−
&= \frac{1}{2} \left|\left[\frac85\cdot2+0\cdot\left(-\frac65\right)+\left(-\frac{8}{5}\right)\cdot(-2)+0\cdot\frac65\right] - \left[\frac65\cdot0+2\cdot\left(-\frac85\right)+\left(-\frac65\right)\cdot0+(-2)\cdot\frac85\right]\right| \\
 
−
&= \frac{1}{2} \left|\left[\frac{16}{5}+\frac{16}{5}\right]-\left[-\frac{16}{5}-\frac{16}{5}\right]\right| \\
 
−
&= \frac{1}{2} \left|\frac{64}{5}\right| \\
 
−
&= \frac{32}{5}.
 
−
\end{align*}</cmath>
 
−
Therefore, the answer is <math>\boxed{\textbf{(D)} ~\frac{8a^2}{a^2+1}}.</math>
 
  
−
Suggested Reading for the Shoelace Formula: https://artofproblemsolving.com/wiki/index.php/Shoelace_Theorem
+
==Solution 3 (Slopes and Intercepts)==
  
−
~MRENTHUSIASM
+
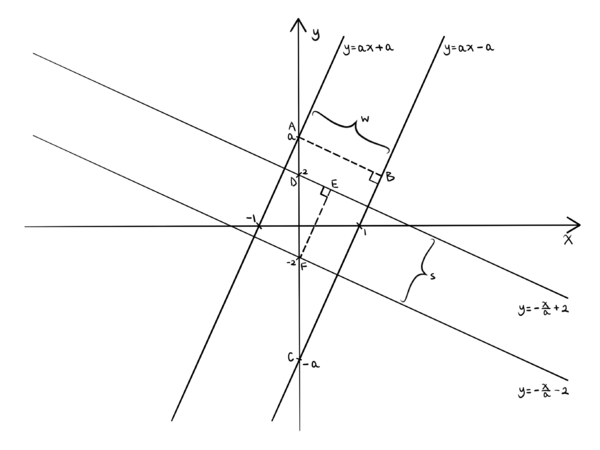
[[File:Diagram of Quadrilateral.png|600px|center]]
  
−
==Solution 3 (Geometry)==
+
The quadrilateral is enclosed by four lines. Similar to Solution 1, we will use the equations from the four cases:
−
Similar to Solution 2, we will use the equations of the four cases:
+
<ol style="margin-left: 1.5em;">
 +
  <li><math>x+ay=2a.</math> This is a line with <math>x</math>-intercept <math>2a,</math> <math>y</math>-intercept <math>2,</math> and slope <math>-\frac 1a.</math></li><p>
 +
  <li><math>x+ay=-2a.</math> This is a line with <math>x</math>-intercept <math>-2a,</math> <math>y</math>-intercept <math>-2,</math> and slope <math>-\frac 1a.</math></li><p>
 +
  <li><math>ax-y=a.</math> This is a line with <math>x</math>-intercept <math>1,</math> <math>y</math>-intercept <math>-a,</math> and slope <math>a.</math></li><p>
 +
  <li><math>ax-y=-a.</math> This is a line with <math>x</math>-intercept <math>-1,</math> <math>y</math>-intercept <math>a,</math> and slope <math>a.</math></li><p>
 +
</ol>
 +
It follows that <math>DF = 4</math> and <math>DE = \sqrt{4^2 - s^2}</math>.
  
−
(1) <math>x+ay=2a.</math> This is a line with <math>x</math>-intercept <math>2a</math>, <math>y</math>-intercept <math>2</math>, and slope <math>-\frac 1a.</math>
+
Because the slope of line <math>y = -\frac{x}{a} + 2</math> is <math>-\frac{1}{a}</math>, <math>\frac{1}{a} = \frac{DE}{EF} = \frac{\sqrt{16-s^2}}{s}</math>, <math>s^2(a^2+1) = 16a^2</math>, <math>s = \frac{4a}{\sqrt{a^2+1}}</math>.
  
−
(2) <math>x+ay=-2a.</math> This is a line with <math>x</math>-intercept <math>-2a</math>, <math>y</math>-intercept <math>-2</math>, and slope <math>-\frac 1a.</math>
+
It follows that <math>AC = 2a</math> and <math>BC = \sqrt{(2a)^2 - w^2}</math>.
  
−
(3)* <math>ax-y=a.</math> This is a line with <math>x</math>-intercept <math>1</math>, <math>y</math>-intercept <math>-a</math>, and slope <math>a.</math>
+
Because the slope of line <math>y = ax - a</math> is <math>a</math>, <math>a = \frac{BC}{AB} = \frac{\sqrt{4a^2-w^2}}{w}</math>, <math>w^2(a^2+1)=4a^2</math>, <math>w=\frac{2a}{\sqrt{a^2+1}}</math>.
  
−
(4)* <math>ax-y=-a.</math> This is a line with <math>x</math>-intercept <math>-1</math>, <math>y</math>-intercept <math>a</math>, and slope <math>a.</math>
+
Therefore, the answer is <cmath>\text{Area} = s \cdot w=\frac{4a}{\sqrt{a^2+1}} \cdot \frac{2a}{\sqrt{a^2+1}} = \boxed{\textbf{(D)} ~\frac{8a^2}{a^2+1}}.</cmath>
  
−
The area of the rectangle created by the four equations can be written as <math>2a\cdot \cos A\cdot4\sin A</math>
+
~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]
  
−
= <math>8a\cos A \cdot \sin A</math>
+
==Solution 4 (Trigonometry)==
 +
Similar to Solution 1, we will use the equations from the four cases:
 +
<ol style="margin-left: 1.5em;">
 +
  <li><math>x+ay=2a.</math> This is a line with <math>x</math>-intercept <math>2a,</math> <math>y</math>-intercept <math>2,</math> and slope <math>-\frac 1a.</math></li><p>
 +
  <li><math>x+ay=-2a.</math> This is a line with <math>x</math>-intercept <math>-2a,</math> <math>y</math>-intercept <math>-2,</math> and slope <math>-\frac 1a.</math></li><p>
 +
  <li><math>ax-y=a.</math> This is a line with <math>x</math>-intercept <math>1,</math> <math>y</math>-intercept <math>-a,</math> and slope <math>a.</math></li><p>
 +
  <li><math>ax-y=-a.</math> This is a line with <math>x</math>-intercept <math>-1,</math> <math>y</math>-intercept <math>a,</math> and slope <math>a.</math></li><p>
 +
</ol>
 +
Let <math>\tan A=a.</math> The area of the rectangle created by the four equations can be written as
 +
<cmath>\begin{align*}
 +
2a\cdot \cos A\cdot4\sin A &= 8a\cos A \cdot \sin A \\
 +
&= 8a\cdot~\frac{1}{\sqrt{a^2+1}}\cdot~\frac{a}{\sqrt{a^2+1}} \\
 +
&= \boxed{\textbf{(D)} ~\frac{8a^2}{a^2+1}}.
 +
\end{align*}</cmath>
 +
~fnothing4994 (Solution)
  
−
= <math>8a\cdot~\frac{1}{\sqrt{a^2+1}}\cdot~\frac{a}{\sqrt{a^2+1}}</math>
+
~MRENTHUSIASM (Code Adjustments)
  
−
= <math>\boxed{\textbf{(D)} ~\frac{8a^2}{a^2+1}}.</math>
+
==Solution 5 (Observations)==
 +
The conditions <math>(x+ay)^2 = 4a^2</math> and <math>(ax-y)^2 = a^2</math> give <math>|x+ay| = |2a|</math> and <math>|ax-y| = |a|</math> or <math>x+ay = \pm 2a</math> and <math>ax-y = \pm a</math>. The slopes here are perpendicular, so the quadrilateral is a rectangle.
 +
Plug in <math>a=1</math> and graph it. We quickly see that the area is <math>2\sqrt{2} \cdot \sqrt{2} = 4</math>, so the answer can't be <math>\textbf{(A)}</math> or <math>\textbf{(B)}</math> by testing the values they give (test it!). Now plug in <math>a=2</math>. We see using a ruler that the sides of the rectangle are about <math>\frac74</math> and <math>\frac72</math>. So the area is about <math>\frac{49}8 = 6.125</math>. Testing <math>\textbf{(C)}</math>, we get <math>\frac{16}3</math> which is clearly less than <math>6</math>, so it is out. Testing <math>\textbf{(D)}</math>, we get <math>\frac{32}5</math> which is near our answer, so we leave it. Testing <math>\textbf{(E)}</math>, we get <math>\frac{16}5</math>, way less than <math>6</math>, so it is out. So, the only plausible answer is <math>\boxed{\textbf{(D)} ~\frac{8a^2}{a^2+1}}</math>.
  
−
(Note: <math>\tan A=</math> slope <math>a</math>)
+
~firebolt360
  
−
-fnothing4994
+
==Solution 6 (Observations)==
 +
Trying <math>a = 1</math> narrows down the choices to options <math>\textbf{(C)}</math>, <math>\textbf{(D)}</math> and <math>\textbf{(E)}</math>. Trying <math>a = 2</math> and <math>a = 3</math> eliminates <math>\textbf{(C)}</math> and <math>\textbf{(E)}</math>, to obtain <math>\boxed{\textbf{(D)} ~\frac{8a^2}{a^2+1}}</math> as our answer. Refer to Solution 2 for a detailed explanation.
  
−
==Solution 4 (bruh moment solution)==
+
~¢
  
−
Trying <math>a = 1</math> narrows down the choices to options <math>\textbf{(C)}</math>, <math>\textbf{(D)}</math> and <math>\textbf{(E)}</math>. Trying <math>a = 2</math> and <math>a = 3</math> eliminates <math>\textbf{(C)}</math> and <math>\textbf{(E)}</math>, to obtain <math>\boxed{\textbf{(D)} ~\frac{8a^2}{a^2+1}}.</math> as our answer. -¢
+
==Solution 7 (Observations: Cheap)==
 +
Note that <math>a=2</math> yields different values for all answer choices. If we put in <math>a=2,</math> we find that the area of the quadrilateral is <math>\frac{32}{5}.</math> This means that the answer must be <math>\boxed{\textbf{(D)} ~\frac{8a^2}{a^2+1}}.</math> Refer to Solution 2 for a detailed explanation.
  
 
== Video Solution by OmegaLearn (System of Equations and Shoelace Formula) ==
 
== Video Solution by OmegaLearn (System of Equations and Shoelace Formula) ==
Line 87: Line 146:
  
 
~ pi_is_3.14
 
~ pi_is_3.14
 +
 +
== Video Solution by MRENTHUSIASM (English & Chinese) ==
 +
https://www.youtube.com/watch?v=oEY-kX4d87M
 +
 +
~MRENTHUSIASM
  
 
==See also==
 
==See also==
 
{{AMC10 box|year=2021|ab=A|num-b=23|num-a=25}}
 
{{AMC10 box|year=2021|ab=A|num-b=23|num-a=25}}
 
{{MAA Notice}}
 
{{MAA Notice}}

Latest revision as of 18:31, 18 November 2022

Problem

The interior of a quadrilateral is bounded by the graphs of $(x+ay)^2 = 4a^2$ and $(ax-y)^2 = a^2$, where $a$ is a positive real number. What is the area of this region in terms of $a$, valid for all $a > 0$?

$\textbf{(A)} ~\frac{8a^2}{(a+1)^2}\qquad\textbf{(B)} ~\frac{4a}{a+1}\qquad\textbf{(C)} ~\frac{8a}{a+1}\qquad\textbf{(D)} ~\frac{8a^2}{a^2+1}\qquad\textbf{(E)} ~\frac{8a}{a^2+1}$

Diagram

Graph in Desmos: https://www.desmos.com/calculator/satawguqsc

~MRENTHUSIASM

Solution 1 (Generalized Value of a)

The cases for $(x+ay)^2 = 4a^2$ are $x+ay = \pm2a,$ or two parallel lines. We rearrange each case and construct the table below: \[\begin{array}{c||c|c|c|c} & & & & \\ [-2.5ex] \textbf{Case} & \textbf{Line's Equation} & \boldsymbol{x}\textbf{-Intercept} & \boldsymbol{y}\textbf{-Intercept} & \textbf{Slope} \\ [0.5ex] \hline & & & & \\ [-1.5ex] 1 & x+ay-2a=0 & 2a & 2 & -\frac1a \\ [2ex] 2 & x+ay+2a=0 & -2a & -2 & -\frac1a \\ [0.75ex] \end{array}\] The cases for $(ax-y)^2 = a^2$ are $ax-y=\pm a,$ or two parallel lines. We rearrange each case and construct the table below: \[\begin{array}{c||c|c|c|c} & & & & \\ [-2.5ex] \textbf{Case} & \textbf{Line's Equation} & \boldsymbol{x}\textbf{-Intercept} & \boldsymbol{y}\textbf{-Intercept} & \textbf{Slope} \\ [0.5ex] \hline & & & & \\ [-1.5ex] 1* & ax-y-a=0 & 1 & -a & a \\ [2ex] 2* & ax-y+a=0 & -1 & a & a \\ [0.75ex] \end{array}\] Since the slopes of intersecting lines $(1)\cap(1*), (1)\cap(2*), (2)\cap(1*),$ and $(2)\cap(2*)$ are negative reciprocals, we get four right angles, from which the quadrilateral is a rectangle.

Two solutions follow from here:

Solution 1.1 (Distance Between Parallel Lines)

Recall that for constants $A,B,C_1$ and $C_2,$ the distance $d$ between parallel lines $\begin{cases} Ax+By+C_1=0 \\ Ax+By+C_2=0 \end{cases}$ is \[d=\frac{\left|C_2-C_1\right|}{\sqrt{A^2+B^2}}.\] From this formula:

  • The distance between lines $(1)$ and $(2)$ is $\frac{4a}{\sqrt{1+a^2}},$ the length of this rectangle.
  • The distance between lines $(1*)$ and $(2*)$ is $\frac{2a}{\sqrt{a^2+1}},$ the width of this rectangle.

The area we seek is \[\frac{4a}{\sqrt{1+a^2}}\cdot\frac{2a}{\sqrt{a^2+1}}=\boxed{\textbf{(D)} ~\frac{8a^2}{a^2+1}}.\] ~MRENTHUSIASM

Solution 1.2 (Distance Between Points)

The solutions to systems of equations $(1)\cap(1*), (1)\cap(2*), (2)\cap(2*), (2)\cap(1*)$ are \[(x,y)=\left(\frac{a(a+2)}{a^2+1},\frac{a(2a-1)}{a^2+1}\right), \left(-\frac{a(a-2)}{a^2+1},\frac{a(2a+1)}{a^2+1}\right), \left(-\frac{a(a+2)}{a^2+1},-\frac{a(2a-1)}{a^2+1}\right), \left(\frac{a(a-2)}{a^2+1},-\frac{a(2a+1)}{a^2+1}\right),\] respectively, which are the consecutive vertices of this rectangle.

By the Distance Formula, the length and width of this rectangle are $\frac{4a\sqrt{a^2+1}}{a^2+1}$ and $\frac{2a\sqrt{a^2+1}}{a^2+1},$ respectively.

The area we seek is \[\frac{4a\sqrt{a^2+1}}{a^2+1}\cdot\frac{2a\sqrt{a^2+1}}{a^2+1}=\boxed{\textbf{(D)} ~\frac{8a^2}{a^2+1}}.\] ~MRENTHUSIASM

Solution 2 (Specified Value of a)

In this solution, we will refer to equations $(1),(2),(1*),$ and $(2*)$ from Solution 1.

Substituting $a=2$ into the answer choices gives

$\textbf{(A)} ~\frac{32}{9}\qquad\textbf{(B)} ~\frac{8}{3}\qquad\textbf{(C)} ~\frac{16}{3}\qquad\textbf{(D)} ~\frac{32}{5}\qquad\textbf{(E)} ~\frac{16}{5}$

At $a=2,$ the solutions to systems of equations $(1)\cap(1*), (1)\cap(2*), (2)\cap(2*), (2)\cap(1*)$ are \[(x,y)=\left(\frac 85, \frac 65\right), (0,2), \left(-\frac 85, -\frac 65\right), (0,-2),\] respectively, which are the consecutive vertices of the quadrilateral.

Two solutions follow from here:

Solution 2.1 (Area of a Rectangle)

From the tables in Solution 1, we conclude that the quadrilateral is a rectangle.

By the Distance Formula, the length and width of this rectangle are $\frac{8\sqrt5}{5}$ and $\frac{4\sqrt5}{5},$ respectively.

The area we seek is \[\frac{8\sqrt5}{5}\cdot\frac{4\sqrt5}{5}=\frac{32}{5},\] from which the answer is $\boxed{\textbf{(D)} ~\frac{8a^2}{a^2+1}}.$

~MRENTHUSIASM

Solution 2.2 (Area of a General Quadrilateral)

Even if we do not recognize that the quadrilateral is a rectangle, we can apply the Shoelace Theorem to its consecutive vertices \begin{align*} (x_1,y_1) &= \left(\frac 85, \frac 65\right), \\ (x_2,y_2) &= (0,2), \\ (x_3,y_3) &= \left(-\frac 85, -\frac 65\right), \\ (x_4,y_4) &= (0,-2). \end{align*} The area we seek is \[\frac{1}{2} \left|(x_1y_2 + x_2y_3 + x_3y_4 + x_4y_1) - (y_1x_2 + y_2x_3 + y_3x_4 + y_4x_1)\right| = \frac{32}{5}.\] from which the answer is $\boxed{\textbf{(D)} ~\frac{8a^2}{a^2+1}}.$

~MRENTHUSIASM

Solution 3 (Slopes and Intercepts)

Diagram of Quadrilateral.png

The quadrilateral is enclosed by four lines. Similar to Solution 1, we will use the equations from the four cases:

  1. $x+ay=2a.$ This is a line with $x$-intercept $2a,$ $y$-intercept $2,$ and slope $-\frac 1a.$

  2. $x+ay=-2a.$ This is a line with $x$-intercept $-2a,$ $y$-intercept $-2,$ and slope $-\frac 1a.$

  3. $ax-y=a.$ This is a line with $x$-intercept $1,$ $y$-intercept $-a,$ and slope $a.$

  4. $ax-y=-a.$ This is a line with $x$-intercept $-1,$ $y$-intercept $a,$ and slope $a.$

It follows that $DF = 4$ and $DE = \sqrt{4^2 - s^2}$.

Because the slope of line $y = -\frac{x}{a} + 2$ is $-\frac{1}{a}$, $\frac{1}{a} = \frac{DE}{EF} = \frac{\sqrt{16-s^2}}{s}$, $s^2(a^2+1) = 16a^2$, $s = \frac{4a}{\sqrt{a^2+1}}$.

It follows that $AC = 2a$ and $BC = \sqrt{(2a)^2 - w^2}$.

Because the slope of line $y = ax - a$ is $a$, $a = \frac{BC}{AB} = \frac{\sqrt{4a^2-w^2}}{w}$, $w^2(a^2+1)=4a^2$, $w=\frac{2a}{\sqrt{a^2+1}}$.

Therefore, the answer is \[\text{Area} = s \cdot w=\frac{4a}{\sqrt{a^2+1}} \cdot \frac{2a}{\sqrt{a^2+1}} = \boxed{\textbf{(D)} ~\frac{8a^2}{a^2+1}}.\]

~isabelchen

Solution 4 (Trigonometry)

Similar to Solution 1, we will use the equations from the four cases:

  1. $x+ay=2a.$ This is a line with $x$-intercept $2a,$ $y$-intercept $2,$ and slope $-\frac 1a.$

  2. $x+ay=-2a.$ This is a line with $x$-intercept $-2a,$ $y$-intercept $-2,$ and slope $-\frac 1a.$

  3. $ax-y=a.$ This is a line with $x$-intercept $1,$ $y$-intercept $-a,$ and slope $a.$

  4. $ax-y=-a.$ This is a line with $x$-intercept $-1,$ $y$-intercept $a,$ and slope $a.$

Let $\tan A=a.$ The area of the rectangle created by the four equations can be written as \begin{align*} 2a\cdot \cos A\cdot4\sin A &= 8a\cos A \cdot \sin A \\ &= 8a\cdot~\frac{1}{\sqrt{a^2+1}}\cdot~\frac{a}{\sqrt{a^2+1}} \\ &= \boxed{\textbf{(D)} ~\frac{8a^2}{a^2+1}}. \end{align*} ~fnothing4994 (Solution)

~MRENTHUSIASM (Code Adjustments)

Solution 5 (Observations)

The conditions $(x+ay)^2 = 4a^2$ and $(ax-y)^2 = a^2$ give $|x+ay| = |2a|$ and $|ax-y| = |a|$ or $x+ay = \pm 2a$ and $ax-y = \pm a$. The slopes here are perpendicular, so the quadrilateral is a rectangle. Plug in $a=1$ and graph it. We quickly see that the area is $2\sqrt{2} \cdot \sqrt{2} = 4$, so the answer can't be $\textbf{(A)}$ or $\textbf{(B)}$ by testing the values they give (test it!). Now plug in $a=2$. We see using a ruler that the sides of the rectangle are about $\frac74$ and $\frac72$. So the area is about $\frac{49}8 = 6.125$. Testing $\textbf{(C)}$, we get $\frac{16}3$ which is clearly less than $6$, so it is out. Testing $\textbf{(D)}$, we get $\frac{32}5$ which is near our answer, so we leave it. Testing $\textbf{(E)}$, we get $\frac{16}5$, way less than $6$, so it is out. So, the only plausible answer is $\boxed{\textbf{(D)} ~\frac{8a^2}{a^2+1}}$.

~firebolt360

Solution 6 (Observations)

Trying $a = 1$ narrows down the choices to options $\textbf{(C)}$, $\textbf{(D)}$ and $\textbf{(E)}$. Trying $a = 2$ and $a = 3$ eliminates $\textbf{(C)}$ and $\textbf{(E)}$, to obtain $\boxed{\textbf{(D)} ~\frac{8a^2}{a^2+1}}$ as our answer. Refer to Solution 2 for a detailed explanation.

~¢

Solution 7 (Observations: Cheap)

Note that $a=2$ yields different values for all answer choices. If we put in $a=2,$ we find that the area of the quadrilateral is $\frac{32}{5}.$ This means that the answer must be $\boxed{\textbf{(D)} ~\frac{8a^2}{a^2+1}}.$ Refer to Solution 2 for a detailed explanation.

Video Solution by OmegaLearn (System of Equations and Shoelace Formula)

https://youtu.be/2iohPYkZpkQ

~ pi_is_3.14

Video Solution by MRENTHUSIASM (English & Chinese)

https://www.youtube.com/watch?v=oEY-kX4d87M

~MRENTHUSIASM

See also

2021 AMC 10A (Problems • Answer Key • Resources)
Preceded by
Problem 23 		Followed by
Problem 25
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2021_AMC_10A_Problems/Problem_24&oldid=182312"