Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2018 AIME II Problems/Problem 14"

m (→‎Solution 2 (Projective))
(→‎Solution 4 (Projective geometry))
 
(15 intermediate revisions by 6 users not shown)
Line 3: Line 3:
 
The incircle <math>\omega</math> of triangle <math>ABC</math> is tangent to <math>\overline{BC}</math> at <math>X</math>. Let <math>Y \neq X</math> be the other intersection of <math>\overline{AX}</math> with <math>\omega</math>. Points <math>P</math> and <math>Q</math> lie on <math>\overline{AB}</math> and <math>\overline{AC}</math>, respectively, so that <math>\overline{PQ}</math> is tangent to <math>\omega</math> at <math>Y</math>. Assume that <math>AP = 3</math>, <math>PB = 4</math>, <math>AC = 8</math>, and <math>AQ = \dfrac{m}{n}</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m+n</math>.
 
The incircle <math>\omega</math> of triangle <math>ABC</math> is tangent to <math>\overline{BC}</math> at <math>X</math>. Let <math>Y \neq X</math> be the other intersection of <math>\overline{AX}</math> with <math>\omega</math>. Points <math>P</math> and <math>Q</math> lie on <math>\overline{AB}</math> and <math>\overline{AC}</math>, respectively, so that <math>\overline{PQ}</math> is tangent to <math>\omega</math> at <math>Y</math>. Assume that <math>AP = 3</math>, <math>PB = 4</math>, <math>AC = 8</math>, and <math>AQ = \dfrac{m}{n}</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m+n</math>.
  
 +
 +
==Diagram==
 +
<asy> size(200); import olympiad; defaultpen(linewidth(1)+fontsize(12));
 +
pair A,B,C,P,Q,Wp,X,Y,Z; B=origin; C=(6.75,0); A=IP(CR(B,7),CR(C,8)); path c=incircle(A,B,C); Wp=IP(c,A--C); Z=IP(c,A--B); X=IP(c,B--C); Y=IP(c,A--X); pair I=incenter(A,B,C); P=extension(A,B,Y,Y+dir(90)*(Y-I)); Q=extension(A,C,P,Y);
 +
draw(A--B--C--cycle, black+1); draw(c^^A--X^^P--Q);
 +
pen p=4+black; dot("$A$",A,N,p); dot("$B$",B,SW,p); dot("$C$",C,SE,p); dot("$X$",X,S,p); dot("$Y$",Y,dir(55),p); dot("$W$",Wp,E,p); dot("$Z$",Z,W,p); dot("$P$",P,W,p); dot("$Q$",Q,E,p); MA("\beta",C,X,A,0.3,black); MA("\alpha",B,A,X,0.7,black); </asy>
  
 
==Solution 1==
 
==Solution 1==
Line 8: Line 14:
  
 
==Solution 2 (Projective)==
 
==Solution 2 (Projective)==
−
Let the incircle of <math>ABC</math> be tangent to <math>AB</math> and <math>AC</math> at <math>M</math> and <math>N</math>. By Brianchon's theorem on tangential hexagons <math>QNCBMP</math> and <math>PYQCXB</math>, we know that <math>MN,CP,BQ</math> and <math>XY</math> are concurrent at a point <math>O</math>. Let <math>PQ \cap BC = Z</math>. Then by La Hire's <math>A</math> lies on the polar of <math>Z</math> so <math>Z</math> lies on the polar of <math>A</math>. Therefore, <math>MN</math> also passes through <math>Z</math>. Then projecting through <math>Z</math>, we have
+
Let the incircle of <math>ABC</math> be tangent to <math>AB</math> and <math>AC</math> at <math>Z</math> and <math>W</math>. By Brianchon's theorem on tangential hexagons <math>QWCBZP</math> and <math>PYQCXB</math>, we know that <math>ZW,CP,BQ</math> and <math>XY</math> are concurrent at a point <math>O</math>. Let <math>PQ \cap BC = M</math>. Then by La Hire's <math>A</math> lies on the polar of <math>M</math> so <math>M</math> lies on the polar of <math>A</math>. Therefore, <math>ZW</math> also passes through <math>M</math>. Then projecting through <math>M</math>, we have
−
<cmath> -1 = (A,O;Y,X) \stackrel{Z}{=} (A,M;P,B) \stackrel{Z}{=} (A,N;Q,C).</cmath>Therefore, <math>\frac{AP \cdot MB}{MP \cdot AB} = 1 \implies \frac{3 \cdot MB}{MP \cdot 7} = 1</math>. Since <math>MB+MP=4</math> we know that <math>MP = \frac{6}{5}</math> and <math>MB = \frac{14}{5}</math>. Therefore, <math>AN = AM = \frac{21}{5}</math> and <math>NC = 8 - \frac{21}{5} = \frac{19}{5}</math>. Since <math>(A,N;Q,C) = -1</math>, we also have <math>\frac{AQ \cdot NC}{NQ \cdot AC} = 1 \implies \frac{AQ \cdot \tfrac{19}{5}}{(\tfrac{21}{5} - AQ) \cdot 8} = 1</math>. Solving for <math>AQ</math>, we obtain <math>AQ = \frac{168}{59} \implies m+n = \boxed{227}</math>.
+
<cmath> -1 = (A,O;Y,X) \stackrel{M}{=} (A,Z;P,B) \stackrel{M}{=} (A,W;Q,C).</cmath>Therefore, <math>\frac{AP \cdot ZB}{MP \cdot AB} = 1 \implies \frac{3 \cdot ZB}{ZP \cdot 7} = 1</math>. Since <math>ZB+ZP=4</math> we know that <math>ZP = \frac{6}{5}</math> and <math>ZB = \frac{14}{5}</math>. Therefore, <math>AW = AZ = \frac{21}{5}</math> and <math>WC = 8 - \frac{21}{5} = \frac{19}{5}</math>. Since <math>(A,W;Q,C) = -1</math>, we also have <math>\frac{AQ \cdot WC}{NQ \cdot AC} = 1 \implies \frac{AQ \cdot \tfrac{19}{5}}{(\tfrac{21}{5} - AQ) \cdot 8} = 1</math>. Solving for <math>AQ</math>, we obtain <math>AQ = \frac{168}{59} \implies m+n = \boxed{227}</math>.
−
 
+
😃
 
-Vfire
 
-Vfire
  
Line 63: Line 69:
  
 
~Solution by <math>BladeRunnerAUG</math> (Frank FYC)
 
~Solution by <math>BladeRunnerAUG</math> (Frank FYC)
 +
 +
==Solution 4 (Projective geometry)==
 +
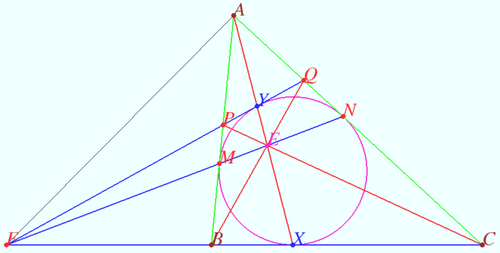
[[File:2018 AIME II 14.png|500px|right]]
 +
<i><b>Claim</b></i>
 +
 +
Let the sides <math>\overline{AB}</math> and <math>\overline{AC}</math> be tangent to <math>\omega</math> at <math>M</math> and <math>N</math>, respectively. Then
 +
lines <math>PQ, MN,</math> and <math>BC</math> are concurrent and lines <math>PC, MN, AX,</math> and <math>BQ</math> are concurrent.
 +
 +
<i><b>Proof</b></i>
 +
 +
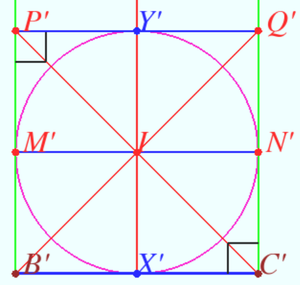
Let <math>E</math> be point of crossing <math>AX</math> and <math>BQ.</math> We make projective transformation such that circle <math>\omega</math> maps into the circle and point <math>E</math> maps into the center of new circle point <math>I.</math> We denote images using notification <math>X \rightarrow X'.</math>
 +
[[File:2018 AIME II 14a.png|300px|right]]
 +
<math>BCQP</math> maps into <math>B'C'Q'P'</math>, so lines <math>B'Q'</math> and  <math>A'X'</math> be the diameters.
 +
This implies <math>P'Q'||B'C', \angle B'P'Q' = \angle B'C'Q' = 90^\circ \implies B'C'Q'P'</math> be a square.
 +
 +
Therefore <math>M'N'</math> be the diameter <math>\implies P'C', B'Q',</math> be diagonals of the square. <math>M'N'</math> and  <math>X'Y'</math> be midlines  which crossing in the center <math>I.</math> Therefore lines <math>PC, MN, AX,</math> and <math>BQ</math> are concurrent.
 +
 +
Lines <math>P'Q'||M'N' ||B'C' \implies PQ, MN</math> and <math>BC</math> are concurrent.
 +
 +
<i><b>Solution</b></i>
 +
The cross-ratio associated with a list of four collinear points <math>A,P,M,D</math> is defined as <cmath>(A,P;M,B)={\frac {AP\cdot MB}{AB\cdot PM}}.</cmath>
 +
The cross-ratio be <i><b>projective invariant</b></i> of a quadruple of collinear points, so
 +
[[File:2018 AIME II 14b.png|300px|right]]
 +
<cmath>(A,P; M,B)  = {\frac {A'P'\cdot M'B'}{A'B'\cdot P'M'}} = \frac {M'B'}{P'M'} = 1.</cmath>
 +
<cmath>(A,P; M,B)={\frac {3\cdot (7 - AM)}{7\cdot (AM - 3)}} = 1 \implies AM = \frac {21}{5} \implies AN = AM =  \frac {21}{5}.</cmath>
 +
[[File:2018 AIME II 14c.png|300px|right]]
 +
<cmath>(A,Q;N,C)={\frac {AQ\cdot NC}{AC\cdot QN}} = \frac {AQ\cdot (AC- AN)}{AC\cdot (AN-AQ)} = 1.</cmath>
 +
<cmath>AQ \cdot (8 - \frac{21}{5}) = 8 \cdot (\frac{21}{5} – AQ) \implies  AQ = \frac{168}{59}.</cmath>
 +
 +
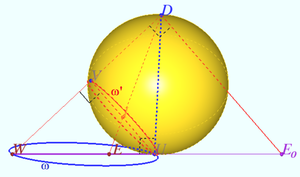
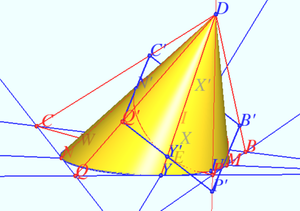
For visuals only, I will show how one can find the perceptor <math>D</math> and the image’s plane.
 +
<math>E_0</math> is image of inversion <math>E</math> with respect <math>\omega.</math>
 +
<math>UW</math> is the diameter of <math>\omega, E,E_0,U,W</math> are collinear.
 +
<math>DU \perp \omega, DE_0\perp WD, UV \perp WD, UV</math> is diameter of <math>\omega'</math>.
 +
 +
Plane of images is perpendicular to <math>WD.</math>
 +
 +
Last diagram shows the result of transformation. Transformation is possible. The end.
 +
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
 +
==Video Solution by Mop 2024==
 +
https://youtu.be/SIs1JFLFzyw
 +
 +
~r00tsOfUnity
 +
 +
==See Also==
 
{{AIME box|year=2018|n=II|num-b=13|num-a=15}}
 
{{AIME box|year=2018|n=II|num-b=13|num-a=15}}
 +
 +
[[Category:Intermediate Geometry Problems]]
 
{{MAA Notice}}
 
{{MAA Notice}}

Latest revision as of 13:32, 28 January 2024

Problem

The incircle $\omega$ of triangle $ABC$ is tangent to $\overline{BC}$ at $X$. Let $Y \neq X$ be the other intersection of $\overline{AX}$ with $\omega$. Points $P$ and $Q$ lie on $\overline{AB}$ and $\overline{AC}$, respectively, so that $\overline{PQ}$ is tangent to $\omega$ at $Y$. Assume that $AP = 3$, $PB = 4$, $AC = 8$, and $AQ = \dfrac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. Find $m+n$.


Diagram

[asy] size(200); import olympiad; defaultpen(linewidth(1)+fontsize(12)); pair A,B,C,P,Q,Wp,X,Y,Z; B=origin; C=(6.75,0); A=IP(CR(B,7),CR(C,8)); path c=incircle(A,B,C); Wp=IP(c,A--C); Z=IP(c,A--B); X=IP(c,B--C); Y=IP(c,A--X); pair I=incenter(A,B,C); P=extension(A,B,Y,Y+dir(90)*(Y-I)); Q=extension(A,C,P,Y); draw(A--B--C--cycle, black+1); draw(c^^A--X^^P--Q); pen p=4+black; dot("$A$",A,N,p); dot("$B$",B,SW,p); dot("$C$",C,SE,p); dot("$X$",X,S,p); dot("$Y$",Y,dir(55),p); dot("$W$",Wp,E,p); dot("$Z$",Z,W,p); dot("$P$",P,W,p); dot("$Q$",Q,E,p); MA("\beta",C,X,A,0.3,black); MA("\alpha",B,A,X,0.7,black); [/asy]

Solution 1

Let the sides $\overline{AB}$ and $\overline{AC}$ be tangent to $\omega$ at $Z$ and $W$, respectively. Let $\alpha = \angle BAX$ and $\beta = \angle AXC$. Because $\overline{PQ}$ and $\overline{BC}$ are both tangent to $\omega$ and $\angle YXC$ and $\angle QYX$ subtend the same arc of $\omega$, it follows that $\angle AYP = \angle QYX = \angle YXC = \beta$. By equal tangents, $PZ = PY$. Applying the Law of Sines to $\triangle APY$ yields \[\frac{AZ}{AP} = 1 + \frac{ZP}{AP} = 1 + \frac{PY}{AP} = 1 + \frac{\sin\alpha}{\sin\beta}.\]Similarly, applying the Law of Sines to $\triangle ABX$ gives \[\frac{AZ}{AB} = 1 - \frac{BZ}{AB} = 1 - \frac{BX}{AB} = 1 - \frac{\sin\alpha}{\sin\beta}.\]It follows that \[2 = \frac{AZ}{AP} + \frac{AZ}{AB} = \frac{AZ}3 + \frac{AZ}7,\]implying $AZ = \tfrac{21}5$. Applying the same argument to $\triangle AQY$ yields \[2 = \frac{AW}{AQ} + \frac{AW}{AC} = \frac{AZ}{AQ} + \frac{AZ}{AC} = \frac{21}5\left(\frac{1}{AQ} + \frac 18\right),\]from which $AQ = \tfrac{168}{59}$. The requested sum is $168 + 59 = \boxed{227}$.

Solution 2 (Projective)

Let the incircle of $ABC$ be tangent to $AB$ and $AC$ at $Z$ and $W$. By Brianchon's theorem on tangential hexagons $QWCBZP$ and $PYQCXB$, we know that $ZW,CP,BQ$ and $XY$ are concurrent at a point $O$. Let $PQ \cap BC = M$. Then by La Hire's $A$ lies on the polar of $M$ so $M$ lies on the polar of $A$. Therefore, $ZW$ also passes through $M$. Then projecting through $M$, we have \[-1 = (A,O;Y,X) \stackrel{M}{=} (A,Z;P,B) \stackrel{M}{=} (A,W;Q,C).\]Therefore, $\frac{AP \cdot ZB}{MP \cdot AB} = 1 \implies \frac{3 \cdot ZB}{ZP \cdot 7} = 1$. Since $ZB+ZP=4$ we know that $ZP = \frac{6}{5}$ and $ZB = \frac{14}{5}$. Therefore, $AW = AZ = \frac{21}{5}$ and $WC = 8 - \frac{21}{5} = \frac{19}{5}$. Since $(A,W;Q,C) = -1$, we also have $\frac{AQ \cdot WC}{NQ \cdot AC} = 1 \implies \frac{AQ \cdot \tfrac{19}{5}}{(\tfrac{21}{5} - AQ) \cdot 8} = 1$. Solving for $AQ$, we obtain $AQ = \frac{168}{59} \implies m+n = \boxed{227}$. 😃 -Vfire

Solution 3 (Combination of Law of Sine and Law of Cosine)

Let the center of the incircle of $\triangle ABC$ be $O$. Link $OY$ and $OX$. Then we have $\angle OYP=\angle OXB=90^{\circ}$

$\because$ $OY=OX$

$\therefore$ $\angle OYX=\angle OXY$

$\therefore$ $\angle PYX=\angle YXB$

$\therefore$ $\sin \angle PYX=\sin \angle YXB=\sin \angle YXC=\sin \angle PYA$

Let the incircle of $ABC$ be tangent to $AB$ and $AC$ at $M$ and $N$, let $MP=YP=x$ and $NQ=YQ=y$.

Use Law of Sine in $\triangle APY$ and $\triangle AXB$, we have

$\frac{\sin \angle PAY}{PY}=\frac{\sin \angle PYA}{PA}$

$\frac{\sin \angle BAX}{BX}=\frac{\sin \angle AXB}{AB}$

therefore we have

$\frac{3}{x}=\frac{7}{4-x}$

Solve this equation, we have $x=\frac{6}{5}$

As a result, $MB=4-x=\frac{14}{5}=BX$, $AM=x+3=\frac{21}{5}=AN$, $NC=8-AN=\frac{19}{5}=XC$, $AQ=\frac{21}{5}-y$, $PQ=\frac{6}{5}+y$

So, $BC=\frac{14}{5}+\frac{19}{5}=\frac{33}{5}$

Use Law of Cosine in $\triangle BAC$ and $\triangle PAQ$, we have

$\cos \angle BAC=\frac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\frac{7^2+8^2-{(\frac{33}{5})}^2}{2\cdot 7\cdot 8}$

$\cos \angle PAQ=\frac{AP^2+AQ^2-PQ^2}{2\cdot AP\cdot AQ}=\frac{3^2+{(\frac{21}{5}-y)}^2-{(\frac{6}{5}+y)}^2}{2\cdot {(\frac{21}{5}-y)}\cdot 3}$

And we have

$\cos \angle BAC=\cos \angle PAQ$

So

$\frac{7^2+8^2-{(\frac{33}{5})}^2}{2\cdot 7\cdot 8}=\frac{3^2+{(\frac{21}{5}-y)}^2-{(\frac{6}{5}+y)}^2}{2\cdot {(\frac{21}{5}-y)}\cdot 3}$

Solve this equation, we have $y=\frac{399}{295}=QN$

As a result, $AQ=AN-QN=\frac{21}{5}-\frac{399}{295}=\frac{168}{59}$

So, the final answer of this question is $168+59=\boxed {227}$

~Solution by $BladeRunnerAUG$ (Frank FYC)

Solution 4 (Projective geometry)

2018 AIME II 14.png

Claim

Let the sides $\overline{AB}$ and $\overline{AC}$ be tangent to $\omega$ at $M$ and $N$, respectively. Then lines $PQ, MN,$ and $BC$ are concurrent and lines $PC, MN, AX,$ and $BQ$ are concurrent.

Proof

Let $E$ be point of crossing $AX$ and $BQ.$ We make projective transformation such that circle $\omega$ maps into the circle and point $E$ maps into the center of new circle point $I.$ We denote images using notification $X \rightarrow X'.$

2018 AIME II 14a.png

$BCQP$ maps into $B'C'Q'P'$, so lines $B'Q'$ and $A'X'$ be the diameters. This implies $P'Q'||B'C', \angle B'P'Q' = \angle B'C'Q' = 90^\circ \implies B'C'Q'P'$ be a square.

Therefore $M'N'$ be the diameter $\implies P'C', B'Q',$ be diagonals of the square. $M'N'$ and $X'Y'$ be midlines which crossing in the center $I.$ Therefore lines $PC, MN, AX,$ and $BQ$ are concurrent.

Lines $P'Q'||M'N' ||B'C' \implies PQ, MN$ and $BC$ are concurrent.

Solution The cross-ratio associated with a list of four collinear points $A,P,M,D$ is defined as \[(A,P;M,B)={\frac {AP\cdot MB}{AB\cdot PM}}.\] The cross-ratio be projective invariant of a quadruple of collinear points, so

2018 AIME II 14b.png

\[(A,P; M,B) = {\frac {A'P'\cdot M'B'}{A'B'\cdot P'M'}} = \frac {M'B'}{P'M'} = 1.\] \[(A,P; M,B)={\frac {3\cdot (7 - AM)}{7\cdot (AM - 3)}} = 1 \implies AM = \frac {21}{5} \implies AN = AM = \frac {21}{5}.\]

2018 AIME II 14c.png

\[(A,Q;N,C)={\frac {AQ\cdot NC}{AC\cdot QN}} = \frac {AQ\cdot (AC- AN)}{AC\cdot (AN-AQ)} = 1.\] \[AQ \cdot (8 - \frac{21}{5}) = 8 \cdot (\frac{21}{5} – AQ) \implies AQ = \frac{168}{59}.\]

For visuals only, I will show how one can find the perceptor $D$ and the image’s plane. $E_0$ is image of inversion $E$ with respect $\omega.$ $UW$ is the diameter of $\omega, E,E_0,U,W$ are collinear. $DU \perp \omega, DE_0\perp WD, UV \perp WD, UV$ is diameter of $\omega'$.

Plane of images is perpendicular to $WD.$

Last diagram shows the result of transformation. Transformation is possible. The end.

vladimir.shelomovskii@gmail.com, vvsss

Video Solution by Mop 2024

https://youtu.be/SIs1JFLFzyw

~r00tsOfUnity

See Also

2018 AIME II (Problems • Answer Key • Resources)
Preceded by
Problem 13 		Followed by
Problem 15
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2018_AIME_II_Problems/Problem_14&oldid=213560"