Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2020 AMC 12B Problems/Problem 12"

(→‎Solution)
m (→‎Solution 5 (Basically Solution 2 With Motivation))
 
(54 intermediate revisions by 22 users not shown)
Line 4: Line 4:
 
<math>\textbf{(A)}\ 96 \qquad\textbf{(B)}\ 98 \qquad\textbf{(C)}\  44\sqrt5 \qquad\textbf{(D)}\ 70\sqrt2 \qquad\textbf{(E)}\ 100</math>
 
<math>\textbf{(A)}\ 96 \qquad\textbf{(B)}\ 98 \qquad\textbf{(C)}\  44\sqrt5 \qquad\textbf{(D)}\ 70\sqrt2 \qquad\textbf{(E)}\ 100</math>
  
−
==Solution==
+
==Diagram==
−
Let <math>O</math> be the center of the circle, and <math>X</math> be the midpoint of <math>\overline{CD}</math>. Let <math>CX=a</math> and <math>EX=b</math>. This implies that <math>DE = a - b</math>. Since <math>CE = CX + EX = a + b</math>, we now want to find <math>(a+b)^2+(a-b)^2=2(a^2+b^2)</math>. Since <math>\angle CXO</math> is a right angle, by Pythagorean theorem <math>a^2 + b^2 = CX^2 + OX^2 = (5\sqrt{2})^2=50</math>. Thus, our answer is <math>2(50)=\boxed{\textbf{(E) } 100}</math>.
+
<asy>
 +
/* Made by Shihan; edited by MRENTHUSIASM */
 +
size(250);
 +
 
 +
pair O, A, B, C, D, E;
 +
O = origin;
 +
A = (-5*sqrt(2),0);
 +
B = (5*sqrt(2),0);
 +
E = (5*sqrt(2)-2*sqrt(5),0);
 +
path p;
 +
p = Circle(O,5*sqrt(2));
 +
C = intersectionpoint(p,E--E+10*dir(135));
 +
D = intersectionpoint(p,E--E+10*dir(-45));
 +
draw(p);
 +
dot(O,linewidth(4));
 +
dot("$A$",A,1.5*dir(A),linewidth(4));
 +
dot("$B$",B,1.5*dir(B),linewidth(4));
 +
dot("$E$",E,1.5*dir(135/2),linewidth(4));
 +
dot("$C$",C,1.5*dir(C),linewidth(4));
 +
dot("$D$",D,1.5*dir(D),linewidth(4));
 +
draw(A--B^^C--D);
 +
label("$45^\circ$",E,3.5*dir(155.5),red+fontsize(10));
 +
label("$5\sqrt2$",midpoint(A--O),S);
 +
label("$2\sqrt5$",midpoint(E--B),S);
 +
</asy>
 +
~Shihan ~MRENTHUSIASM
 +
 
 +
==Solution 1 (Pythagorean Theorem) ==
 +
Let <math>O</math> be the center of the circle, and <math>X</math> be the midpoint of <math>\overline{CD}</math>. Let <math>CX=a</math> and <math>EX=b</math>. This implies that <math>DE = a - b</math>. Since <math>CE = CX + EX = a + b</math>, we now want to find <math>(a+b)^2+(a-b)^2=2(a^2+b^2)</math>. Since <math>\angle CXO</math> is a right angle, by Pythagorean theorem <math>a^2 + b^2 = CX^2 + OX^2 = (5\sqrt{2})^2=50</math>. Thus, our answer is <math>2\times50=\boxed{\textbf{(E)}\ 100}</math>.  
  
 
~JHawk0224
 
~JHawk0224
 +
 +
==Solution 2 (Power of a Point)==
 +
Let <math>O</math> be the center of the circle, and <math>X</math> be the midpoint of <math>CD</math>. Draw triangle <math>OCD</math>, and median <math>OX</math>. Because <math>OC = OD</math>, <math>OCD</math> is isosceles, so <math>OX</math> is also an altitude of <math>OCD</math>. <math>OE = 5\sqrt2 - 2\sqrt5</math>, and because angle <math>OEC</math> is <math>45</math> degrees and triangle <math>OXE</math> is right, <math>OX = EX = \frac{5\sqrt2 - 2\sqrt5}{\sqrt2} = 5 - \sqrt{10}</math>. Because triangle <math>OXC</math> is right, <math>CX = \sqrt{(5\sqrt2)^2 - (5 - \sqrt{10})^2} = \sqrt{15 + 10\sqrt{10}}</math>. Thus, <math>CD = 2\sqrt{15 + 10\sqrt{10}}</math>.
 +
 +
We are looking for <math>CE^2</math> + <math>DE^2</math> which is also <math>(CE + DE)^2 - 2 \cdot CE \cdot DE</math>.
 +
 +
Because <math>CE + DE = CD = 2\sqrt{15 + 10\sqrt{10}}</math>, <math>(CE + DE)^2 = CD^2=4(15 + 10\sqrt{10}) = 60 + 40\sqrt{10}</math>.
 +
 +
By Power of a Point, <math>CE \cdot DE = AE \cdot BE = 2\sqrt5\cdot(10\sqrt2 - 2\sqrt5) = 20\sqrt{10} - 20</math>, so <math>2 \cdot CE \cdot DE = 40\sqrt{10} - 40</math>.
 +
 +
Finally, <math>CE^2 + DE^2 = (CE+ED)^2-2\cdot CE \cdot DE=(60 + 40\sqrt{10}) - (40\sqrt{10} - 40) = \boxed{\textbf{(E)}\ 100}</math>.
 +
 +
==Solution 3 (Law of Cosines)==
 +
Let <math>O</math> be the center of the circle. Notice how <math>OC = OD = r</math>, where <math>r</math> is the radius of the circle. By applying the law of cosines on triangle <math>OCE</math>, <cmath>r^2=CE^2+OE^2-2(CE)(OE)\cos{45}=CE^2+OE^2-(CE)(OE)\sqrt{2}.</cmath>
 +
 +
Similarly, by applying the law of cosines on triangle <math>ODE</math>, <cmath>r^2=DE^2+OE^2-2(DE)(OE)\cos{135}=DE^2+OE^2+(DE)(OE)\sqrt{2}.</cmath>
 +
 +
By subtracting these two equations, we get <cmath>CE^2-DE^2-(CE)(OE)\sqrt{2}-(DE)(OE)\sqrt{2}=0.</cmath> We can rearrange it to get <cmath>CE^2-DE^2=(CE)(OE)\sqrt{2}+(DE)(OE)\sqrt{2}=(CE+DE)(OE\sqrt{2}).</cmath>
 +
 +
Because both <math>CE</math> and <math>DE</math> are both positive, we can safely divide both sides by <math>(CE+DE)</math> to obtain <math>CE-DE=OE\sqrt{2}</math>. Because <math>OE = OB - BE = 5\sqrt{2} - 2\sqrt{5}</math>, <cmath>(CE-DE)^2 = CE^2+DE^2 - 2(CE)(DE) = (OE\sqrt{2})^2 =2(5\sqrt{2} - 2\sqrt{5})^2 = 140 - 40\sqrt{10}.</cmath>
 +
 +
Through power of a point, we can find out that <math>(CE)(DE)=20\sqrt{10} - 20</math>, so <cmath>CE^2+DE^2 = (CE-DE)^2+ 2(CE)(DE)= (140 - 40\sqrt{10}) + 2(20\sqrt{10} - 20) = \boxed{\textbf{(E)}\ 100}.</cmath>
 +
 +
~Math_Wiz_3.14 (legibility changes by eagleye)
 +
 +
==Solution 4 (Reflections)==
 +
<asy>
 +
/* Made by sofas103; edited by MRENTHUSIASM */
 +
size(250);
 +
 +
pair O, A, B, C, D, E, D1;
 +
O = origin;
 +
A = (-5*sqrt(2),0);
 +
B = (5*sqrt(2),0);
 +
E = (5*sqrt(2)-2*sqrt(5),0);
 +
path p;
 +
p = Circle(O,5*sqrt(2));
 +
C = intersectionpoint(p,E--E+10*dir(135));
 +
D = intersectionpoint(p,E--E+10*dir(-45));
 +
D1 = (D.x,-D.y);
 +
draw(p);
 +
dot("$O$",O,1.5*S,linewidth(4));
 +
dot("$A$",A,1.5*dir(A),linewidth(4));
 +
dot("$B$",B,1.5*dir(B),linewidth(4));
 +
dot("$E$",E,1.5*dir(180+135/2),linewidth(4));
 +
dot("$C$",C,1.5*dir(C),linewidth(4));
 +
dot("$D$",D,1.5*dir(D),linewidth(4));
 +
dot("$D'$",D1,1.5*dir(D1),linewidth(4));
 +
draw(A--B^^C--D^^C--D1--O--cycle^^D1--E);
 +
</asy>
 +
Let <math>O</math> be the center of the circle. By reflecting <math>D</math> across the line <math>AB</math> to produce <math>D'</math>, we have that <math>\angle BED'=45</math>. Since <math>\angle AEC=45</math>, <math>\angle CED'=90</math>. Since <math>DE=ED'</math>, by the Pythagorean Theorem, our desired solution is just <math>CD'^2</math>.
 +
Looking next to circle arcs, we know that <math>\angle AEC=\frac{\overarc{AC}+\overarc{BD}}{2}=45</math>, so <math>\overarc{AC}+\overarc{BD}=90</math>. Since <math>\overarc{BD'}=\overarc{BD}</math>, and <math>\overarc{AC}+\overarc{BD'}+\overarc{CD'}=180</math>, <math>\overarc{CD'}=90</math>. Thus, <math>\angle COD'=90</math>.
 +
Since <math>OC=OD'=5\sqrt{2}</math>, by the Pythagorean Theorem, the desired <math>CD'^2= \boxed{\textbf{(E)}\ 100}</math>.
 +
 +
~sofas103
 +
 +
== Solution 5 (Basically Solution 2 With Motivation) ==
 +
 +
Basically, by PoP, you have that <cmath>CE \times DE = (10\sqrt{2}-2\sqrt{5})(2\sqrt{5}) = 20\sqrt{10} - 20.</cmath> Therefore, as <math>CE^2 + DE^2 = (CD)^2 - 2(CE \times DE),</math> basically, once you find <math>CD^2,</math> the problem is done. Now, this is an IMPORTANT concept: If you have a circle which you know the radius of and you want to find the length of a chord of that circle, drop an altitude from the center of the circle to the chord to find distance between the center of the circle and the chord.
 +
 +
In this case, let <math>M</math> be the midpoint of chord <math>CD.</math> Notice that now we can use our <math>45^\circ{}</math> angle, since <math>OME</math> is a <math>45^\circ{}-45^\circ{}-90^\circ{}</math> triangle so that <math>ME = x</math> and <math>OE = x\sqrt{2}.</math> However, we have that <math>OE = 5\sqrt{2}-2\sqrt{5},</math> so that <math>x = 5 - \sqrt{10}.</math> Now, notice that <math>x^2 = 35 - 10\sqrt{10},</math> so that <cmath>CM^2 = 50 - x^2 = 50 - (35 - 10\sqrt{10}) = 15 + 10 \sqrt{10}</cmath> and <cmath>CD^2 = 60 + 40\sqrt{10}.</cmath> Therefore, <cmath>CE^2 + DE^2 = CD^2 - 2(CE \times DE) = (60+40\sqrt{10}) - 2(2\sqrt{10} - 20) = (60+40\sqrt{10}) + (40-40\sqrt{10}) = \boxed{\textbf{(E)}\ 100}.</cmath>
 +
 +
This may not be the “shortest solution”, but in my opinion is very well motivated and doesn’t require much creativity. [Not requiring much creativity, it also saves more time than you’d think. ;)]
 +
 +
~ Professor-Mom
 +
 +
== Solution 6 (Double Power of a Point) ==
 +
 +
<asy>
 +
/* Made by sofas103; edited by MRENTHUSIASM */
 +
size(250);
 +
 +
pair O, A, B, C, D, E, P, Q;
 +
O = origin;
 +
A = (-5*sqrt(2),0);
 +
B = (5*sqrt(2),0);
 +
E = (5*sqrt(2)-2*sqrt(5),0);
 +
P = (5*sqrt(2), -4.5);
 +
Q=(5*sqrt(2)-2*sqrt(5)-0.5, 0);
 +
path p;
 +
p = Circle(O,5*sqrt(2));
 +
C = intersectionpoint(p,E--E+10*dir(135));
 +
D = intersectionpoint(p,E--E+10*dir(-45));
 +
draw(p);
 +
dot("$A$",A,1.5*dir(A),linewidth(4));
 +
dot("$B$",B,1.5*dir(B),linewidth(4));
 +
dot("$E$",E,1.5*dir(180+135/2),linewidth(4));
 +
dot("$C$",C,1.5*dir(C),linewidth(4));
 +
dot("$D$",D,1.5*dir(D),linewidth(4));
 +
dot("$P$",P,1.5*dir(P),linewidth(4));
 +
label("$45^{\circ}$",Q,NW);
 +
draw(A--B^^C--P--B);
 +
draw((5*sqrt(2), 0)--(5*sqrt(2)-0.4, 0)--(5*sqrt(2)-0.4, -0.4)--(5*sqrt(2), -0.4));
 +
</asy>
 +
For ease of notation, let <math>x = DE</math> and <math>y=EC</math>.
 +
Extend <math>\overline{CD}</math> to point <math>P</math> until <math>\overline{BP}</math> is perpendicular to <math>AB</math>. It's given that <math>\angle AEC = 45^{\circ}</math>, so, by vertical angles, we have <math>\angle BEP = \angle EPB = 45^{\circ}</math>.
 +
 +
Since <math>PEB</math> is a <math>45-45-90</math> right triangle, we have <math>BE = BP = 2\sqrt{5}</math> and <math>PE=2\sqrt{10}</math>. Hence, <math>PD = 2\sqrt{10}-x.</math>
 +
 +
By Power of a Point, we have
 +
 +
<cmath>PB^2 = PD\cdot PC</cmath>
 +
<cmath>20 = \left(2\sqrt{10}-x\right)\left(y + 2\sqrt{10}\right).</cmath>
 +
 +
Isolating the variables after expanding gives <math>x-y = 2\sqrt{10}-10.</math>
 +
 +
Using Power of a Point again, we have
 +
 +
<cmath>DE\cdot EC = BE\cdot EA</cmath>
 +
<cmath>xy = 2\sqrt{5}\left(10\sqrt{2}-2\sqrt{5} \right)</cmath>
 +
<cmath>xy = 20\sqrt{10}-20.</cmath>
 +
To get <math>x^2 + y^2</math>, we can perform the operation <math>(x-y)^2 + 2xy</math>. Plugging these values in,
 +
 +
<cmath>(x-y)^2 + 2xy = \left(2\sqrt{10}-10\right)^2 + 2\left(20\sqrt{10}-20\right)</cmath>
 +
<cmath> = 40 + 100 - 40\sqrt{10} + 40\sqrt{10} - 40 = \boxed{\textbf{(E)}\ 100}</cmath>
 +
 +
-Benedict T (countmath1)
 +
 +
== Solution 7 (Cheating) ==
 +
 +
Perhaps not reliable in general, but very useful as a last resort.
 +
The choice of the radius <math>5\sqrt2</math> is strange, and is probably motivated by a nice answer in the end, so we only consider integer options. Notice that a 5 also appears in the condition <math>BE=2\sqrt5</math>, therefore it will likely be present in the answer as well; the only integer containing a factor of 5 amongst the choices is 100, thus the answer is  <math>\boxed{\textbf{(E)}\ 100}</math>
 +
 +
~Maths357
 +
 +
== Solution 7 (Coordinate Geometry + Vieta) ==
 +
 +
set the origin at E (instead of circle center O) will reduce calculation.
 +
line CD is y= -x , 
 +
let OE = a , circle radius r=<math>5\sqrt{2}</math>, 
 +
circle <math>(x + a)^2 + y^2 = r^2</math>  intersects line y = -x at 2 points <math> C(X_c, Y_c)</math> and <math> D(X_d, Y_d) </math>
 +
<math>X_c = -Y_c </math> , <math>X_d = -Y_d </math>
 +
 +
substitute y with x , circle becomes  <math>(x + a)^2 + y^2 = (x + a)^2 + (-x)^2 = 2x^2 + 2ax + a^2 - r^2 = 0 </math>
 +
 +
<math>X_c , X_d</math> will be 2 roots of above quadratic and we will apply vieta <math>X_c+ X_d , X_c \cdot X_d </math> below
 +
 +
<cmath> CE^2 + DE^2 = ( (-X_c) + Y_c)^2 +  ( X_d + (- Y_d) )^2 \\
 +
= ( (-X_c) + (-X_c))^2 +  ( X_d + (X_d) )^2  \\
 +
= 4 (X_c^2 + X_d^2) \\
 +
= 4 ((X_c + X_d)^2) -  2X_cX_d \\
 +
= 4 ( (\frac{-2a}{2 \cdot  2})^2 + \frac{a^2- r^2}{2} )
 +
 +
</cmath>
 +
 +
plug in a = OE  = OB - OE  = <math> 5\sqrt{2} - 2 \sqrt{5} </math> and <math>r = 5\sqrt{2}</math> we get answer <math>\boxed{\textbf{(E) }100}</math>.
 +
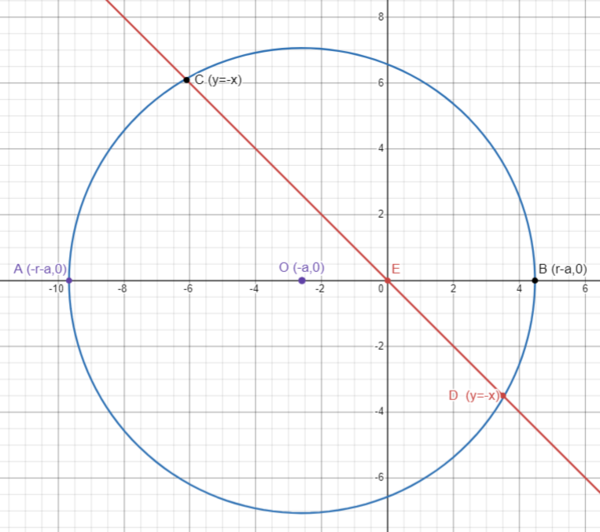
[[Image:2020_AMC_12B_P20.PNG|thumb|center|600px]]
 +
~[https://artofproblemsolving.com/wiki/index.php/User:Cyantist luckuso]
 +
 +
== Video Solution by OmegaLearn ==
 +
https://youtu.be/HIPZ3nj_sT8?t=227
 +
 +
~ pi_is_3.14
 +
 +
==Video Solution by On The Spot STEM==
 +
https://www.youtube.com/watch?v=h-hhRa93lK4
 +
 +
==Video Solution by TheBeautyOfMath==
 +
 +
https://youtu.be/0xgTR3UEqbQ
  
 
==See Also==
 
==See Also==

Latest revision as of 04:41, 4 November 2024

Problem

Let $\overline{AB}$ be a diameter in a circle of radius $5\sqrt2.$ Let $\overline{CD}$ be a chord in the circle that intersects $\overline{AB}$ at a point $E$ such that $BE=2\sqrt5$ and $\angle AEC = 45^{\circ}.$ What is $CE^2+DE^2?$

$\textbf{(A)}\ 96 \qquad\textbf{(B)}\ 98 \qquad\textbf{(C)}\ 44\sqrt5 \qquad\textbf{(D)}\ 70\sqrt2 \qquad\textbf{(E)}\ 100$

Diagram

[asy] /* Made by Shihan; edited by MRENTHUSIASM */ size(250); pair O, A, B, C, D, E; O = origin; A = (-5*sqrt(2),0); B = (5*sqrt(2),0); E = (5*sqrt(2)-2*sqrt(5),0); path p; p = Circle(O,5*sqrt(2)); C = intersectionpoint(p,E--E+10*dir(135)); D = intersectionpoint(p,E--E+10*dir(-45)); draw(p); dot(O,linewidth(4)); dot("$A$",A,1.5*dir(A),linewidth(4)); dot("$B$",B,1.5*dir(B),linewidth(4)); dot("$E$",E,1.5*dir(135/2),linewidth(4)); dot("$C$",C,1.5*dir(C),linewidth(4)); dot("$D$",D,1.5*dir(D),linewidth(4)); draw(A--B^^C--D); label("$45^\circ$",E,3.5*dir(155.5),red+fontsize(10)); label("$5\sqrt2$",midpoint(A--O),S); label("$2\sqrt5$",midpoint(E--B),S); [/asy] ~Shihan ~MRENTHUSIASM

Solution 1 (Pythagorean Theorem)

Let $O$ be the center of the circle, and $X$ be the midpoint of $\overline{CD}$. Let $CX=a$ and $EX=b$. This implies that $DE = a - b$. Since $CE = CX + EX = a + b$, we now want to find $(a+b)^2+(a-b)^2=2(a^2+b^2)$. Since $\angle CXO$ is a right angle, by Pythagorean theorem $a^2 + b^2 = CX^2 + OX^2 = (5\sqrt{2})^2=50$. Thus, our answer is $2\times50=\boxed{\textbf{(E)}\ 100}$.

~JHawk0224

Solution 2 (Power of a Point)

Let $O$ be the center of the circle, and $X$ be the midpoint of $CD$. Draw triangle $OCD$, and median $OX$. Because $OC = OD$, $OCD$ is isosceles, so $OX$ is also an altitude of $OCD$. $OE = 5\sqrt2 - 2\sqrt5$, and because angle $OEC$ is $45$ degrees and triangle $OXE$ is right, $OX = EX = \frac{5\sqrt2 - 2\sqrt5}{\sqrt2} = 5 - \sqrt{10}$. Because triangle $OXC$ is right, $CX = \sqrt{(5\sqrt2)^2 - (5 - \sqrt{10})^2} = \sqrt{15 + 10\sqrt{10}}$. Thus, $CD = 2\sqrt{15 + 10\sqrt{10}}$.

We are looking for $CE^2$ + $DE^2$ which is also $(CE + DE)^2 - 2 \cdot CE \cdot DE$.

Because $CE + DE = CD = 2\sqrt{15 + 10\sqrt{10}}$, $(CE + DE)^2 = CD^2=4(15 + 10\sqrt{10}) = 60 + 40\sqrt{10}$.

By Power of a Point, $CE \cdot DE = AE \cdot BE = 2\sqrt5\cdot(10\sqrt2 - 2\sqrt5) = 20\sqrt{10} - 20$, so $2 \cdot CE \cdot DE = 40\sqrt{10} - 40$.

Finally, $CE^2 + DE^2 = (CE+ED)^2-2\cdot CE \cdot DE=(60 + 40\sqrt{10}) - (40\sqrt{10} - 40) = \boxed{\textbf{(E)}\ 100}$.

Solution 3 (Law of Cosines)

Let $O$ be the center of the circle. Notice how $OC = OD = r$, where $r$ is the radius of the circle. By applying the law of cosines on triangle $OCE$, \[r^2=CE^2+OE^2-2(CE)(OE)\cos{45}=CE^2+OE^2-(CE)(OE)\sqrt{2}.\]

Similarly, by applying the law of cosines on triangle $ODE$, \[r^2=DE^2+OE^2-2(DE)(OE)\cos{135}=DE^2+OE^2+(DE)(OE)\sqrt{2}.\]

By subtracting these two equations, we get \[CE^2-DE^2-(CE)(OE)\sqrt{2}-(DE)(OE)\sqrt{2}=0.\] We can rearrange it to get \[CE^2-DE^2=(CE)(OE)\sqrt{2}+(DE)(OE)\sqrt{2}=(CE+DE)(OE\sqrt{2}).\]

Because both $CE$ and $DE$ are both positive, we can safely divide both sides by $(CE+DE)$ to obtain $CE-DE=OE\sqrt{2}$. Because $OE = OB - BE = 5\sqrt{2} - 2\sqrt{5}$, \[(CE-DE)^2 = CE^2+DE^2 - 2(CE)(DE) = (OE\sqrt{2})^2 =2(5\sqrt{2} - 2\sqrt{5})^2 = 140 - 40\sqrt{10}.\]

Through power of a point, we can find out that $(CE)(DE)=20\sqrt{10} - 20$, so \[CE^2+DE^2 = (CE-DE)^2+ 2(CE)(DE)= (140 - 40\sqrt{10}) + 2(20\sqrt{10} - 20) = \boxed{\textbf{(E)}\ 100}.\]

~Math_Wiz_3.14 (legibility changes by eagleye)

Solution 4 (Reflections)

[asy] /* Made by sofas103; edited by MRENTHUSIASM */ size(250); pair O, A, B, C, D, E, D1; O = origin; A = (-5*sqrt(2),0); B = (5*sqrt(2),0); E = (5*sqrt(2)-2*sqrt(5),0); path p; p = Circle(O,5*sqrt(2)); C = intersectionpoint(p,E--E+10*dir(135)); D = intersectionpoint(p,E--E+10*dir(-45)); D1 = (D.x,-D.y); draw(p); dot("$O$",O,1.5*S,linewidth(4)); dot("$A$",A,1.5*dir(A),linewidth(4)); dot("$B$",B,1.5*dir(B),linewidth(4)); dot("$E$",E,1.5*dir(180+135/2),linewidth(4)); dot("$C$",C,1.5*dir(C),linewidth(4)); dot("$D$",D,1.5*dir(D),linewidth(4)); dot("$D'$",D1,1.5*dir(D1),linewidth(4)); draw(A--B^^C--D^^C--D1--O--cycle^^D1--E); [/asy] Let $O$ be the center of the circle. By reflecting $D$ across the line $AB$ to produce $D'$, we have that $\angle BED'=45$. Since $\angle AEC=45$, $\angle CED'=90$. Since $DE=ED'$, by the Pythagorean Theorem, our desired solution is just $CD'^2$. Looking next to circle arcs, we know that $\angle AEC=\frac{\overarc{AC}+\overarc{BD}}{2}=45$, so $\overarc{AC}+\overarc{BD}=90$. Since $\overarc{BD'}=\overarc{BD}$, and $\overarc{AC}+\overarc{BD'}+\overarc{CD'}=180$, $\overarc{CD'}=90$. Thus, $\angle COD'=90$. Since $OC=OD'=5\sqrt{2}$, by the Pythagorean Theorem, the desired $CD'^2= \boxed{\textbf{(E)}\ 100}$.

~sofas103

Solution 5 (Basically Solution 2 With Motivation)

Basically, by PoP, you have that \[CE \times DE = (10\sqrt{2}-2\sqrt{5})(2\sqrt{5}) = 20\sqrt{10} - 20.\] Therefore, as $CE^2 + DE^2 = (CD)^2 - 2(CE \times DE),$ basically, once you find $CD^2,$ the problem is done. Now, this is an IMPORTANT concept: If you have a circle which you know the radius of and you want to find the length of a chord of that circle, drop an altitude from the center of the circle to the chord to find distance between the center of the circle and the chord.

In this case, let $M$ be the midpoint of chord $CD.$ Notice that now we can use our $45^\circ{}$ angle, since $OME$ is a $45^\circ{}-45^\circ{}-90^\circ{}$ triangle so that $ME = x$ and $OE = x\sqrt{2}.$ However, we have that $OE = 5\sqrt{2}-2\sqrt{5},$ so that $x = 5 - \sqrt{10}.$ Now, notice that $x^2 = 35 - 10\sqrt{10},$ so that \[CM^2 = 50 - x^2 = 50 - (35 - 10\sqrt{10}) = 15 + 10 \sqrt{10}\] and \[CD^2 = 60 + 40\sqrt{10}.\] Therefore, \[CE^2 + DE^2 = CD^2 - 2(CE \times DE) = (60+40\sqrt{10}) - 2(2\sqrt{10} - 20) = (60+40\sqrt{10}) + (40-40\sqrt{10}) = \boxed{\textbf{(E)}\ 100}.\]

This may not be the “shortest solution”, but in my opinion is very well motivated and doesn’t require much creativity. [Not requiring much creativity, it also saves more time than you’d think. ;)]

~ Professor-Mom

Solution 6 (Double Power of a Point)

[asy] /* Made by sofas103; edited by MRENTHUSIASM */ size(250); pair O, A, B, C, D, E, P, Q; O = origin; A = (-5*sqrt(2),0); B = (5*sqrt(2),0); E = (5*sqrt(2)-2*sqrt(5),0); P = (5*sqrt(2), -4.5); Q=(5*sqrt(2)-2*sqrt(5)-0.5, 0); path p; p = Circle(O,5*sqrt(2)); C = intersectionpoint(p,E--E+10*dir(135)); D = intersectionpoint(p,E--E+10*dir(-45)); draw(p); dot("$A$",A,1.5*dir(A),linewidth(4)); dot("$B$",B,1.5*dir(B),linewidth(4)); dot("$E$",E,1.5*dir(180+135/2),linewidth(4)); dot("$C$",C,1.5*dir(C),linewidth(4)); dot("$D$",D,1.5*dir(D),linewidth(4)); dot("$P$",P,1.5*dir(P),linewidth(4)); label("$45^{\circ}$",Q,NW); draw(A--B^^C--P--B); draw((5*sqrt(2), 0)--(5*sqrt(2)-0.4, 0)--(5*sqrt(2)-0.4, -0.4)--(5*sqrt(2), -0.4)); [/asy] For ease of notation, let $x = DE$ and $y=EC$. Extend $\overline{CD}$ to point $P$ until $\overline{BP}$ is perpendicular to $AB$. It's given that $\angle AEC = 45^{\circ}$, so, by vertical angles, we have $\angle BEP = \angle EPB = 45^{\circ}$.

Since $PEB$ is a $45-45-90$ right triangle, we have $BE = BP = 2\sqrt{5}$ and $PE=2\sqrt{10}$. Hence, $PD = 2\sqrt{10}-x.$

By Power of a Point, we have

\[PB^2 = PD\cdot PC\] \[20 = \left(2\sqrt{10}-x\right)\left(y + 2\sqrt{10}\right).\]

Isolating the variables after expanding gives $x-y = 2\sqrt{10}-10.$

Using Power of a Point again, we have

\[DE\cdot EC = BE\cdot EA\] \[xy = 2\sqrt{5}\left(10\sqrt{2}-2\sqrt{5} \right)\] \[xy = 20\sqrt{10}-20.\] To get $x^2 + y^2$, we can perform the operation $(x-y)^2 + 2xy$. Plugging these values in,

\[(x-y)^2 + 2xy = \left(2\sqrt{10}-10\right)^2 + 2\left(20\sqrt{10}-20\right)\] \[= 40 + 100 - 40\sqrt{10} + 40\sqrt{10} - 40 = \boxed{\textbf{(E)}\ 100}\]

-Benedict T (countmath1)

Solution 7 (Cheating)

Perhaps not reliable in general, but very useful as a last resort. The choice of the radius $5\sqrt2$ is strange, and is probably motivated by a nice answer in the end, so we only consider integer options. Notice that a 5 also appears in the condition $BE=2\sqrt5$, therefore it will likely be present in the answer as well; the only integer containing a factor of 5 amongst the choices is 100, thus the answer is $\boxed{\textbf{(E)}\ 100}$

~Maths357

Solution 7 (Coordinate Geometry + Vieta)

set the origin at E (instead of circle center O) will reduce calculation. line CD is y= -x , let OE = a , circle radius r=$5\sqrt{2}$, circle $(x + a)^2 + y^2 = r^2$ intersects line y = -x at 2 points $C(X_c, Y_c)$ and $D(X_d, Y_d)$ $X_c = -Y_c$ , $X_d = -Y_d$

substitute y with x , circle becomes $(x + a)^2 + y^2 = (x + a)^2 + (-x)^2 = 2x^2 + 2ax + a^2 - r^2 = 0$

$X_c , X_d$ will be 2 roots of above quadratic and we will apply vieta $X_c+ X_d , X_c \cdot X_d$ below

\[CE^2 + DE^2 = ( (-X_c) + Y_c)^2 + ( X_d + (- Y_d) )^2 \\ = ( (-X_c) + (-X_c))^2 + ( X_d + (X_d) )^2 \\ = 4 (X_c^2 + X_d^2) \\ = 4 ((X_c + X_d)^2) - 2X_cX_d \\ = 4 ( (\frac{-2a}{2 \cdot 2})^2 + \frac{a^2- r^2}{2} )\]

plug in a = OE = OB - OE = $5\sqrt{2} - 2 \sqrt{5}$ and $r = 5\sqrt{2}$ we get answer $\boxed{\textbf{(E) }100}$.

2020 AMC 12B P20.PNG

~luckuso

Video Solution by OmegaLearn

https://youtu.be/HIPZ3nj_sT8?t=227

~ pi_is_3.14

Video Solution by On The Spot STEM

https://www.youtube.com/watch?v=h-hhRa93lK4

Video Solution by TheBeautyOfMath

https://youtu.be/0xgTR3UEqbQ

See Also

2020 AMC 12B (Problems • Answer Key • Resources)
Preceded by
Problem 11 		Followed by
Problem 13
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2020_AMC_12B_Problems/Problem_12&oldid=231530"