Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2017 AIME I Problems/Problem 4"

(→‎Solution 3 (Heron's Formula))
(→‎Solution)
 
(11 intermediate revisions by 7 users not shown)
Line 1: Line 1:
−
==Problem 4==
+
==Problem ==
 
A pyramid has a triangular base with side lengths <math>20</math>, <math>20</math>, and <math>24</math>. The three edges of the pyramid from the three corners of the base to the fourth vertex of the pyramid all have length <math>25</math>. The volume of the pyramid is <math>m\sqrt{n}</math>, where <math>m</math> and <math>n</math> are positive integers, and <math>n</math> is not divisible by the square of any prime. Find <math>m+n</math>.
 
A pyramid has a triangular base with side lengths <math>20</math>, <math>20</math>, and <math>24</math>. The three edges of the pyramid from the three corners of the base to the fourth vertex of the pyramid all have length <math>25</math>. The volume of the pyramid is <math>m\sqrt{n}</math>, where <math>m</math> and <math>n</math> are positive integers, and <math>n</math> is not divisible by the square of any prime. Find <math>m+n</math>.
  
Line 9: Line 9:
 
<cmath>\overline {OM} + \overline {OC} = \overline {CM} = 16</cmath>
 
<cmath>\overline {OM} + \overline {OC} = \overline {CM} = 16</cmath>
  
−
Let <math>\overline {OM} = d</math>.
+
Let <math>\overline {OM} = d</math>. Then <math>OC=OA=\sqrt{d^2+12^2}.</math>
 
Equation <math>(1)</math>:
 
Equation <math>(1)</math>:
 
<cmath>d + \sqrt {d^2 + 144} = 16</cmath>
 
<cmath>d + \sqrt {d^2 + 144} = 16</cmath>
Line 47: Line 47:
 
This simplifies to <math>V = 800\sqrt {3}</math>, so <math>m+n = \boxed {803}</math>.
 
This simplifies to <math>V = 800\sqrt {3}</math>, so <math>m+n = \boxed {803}</math>.
  
−
==Shortcut==
+
 
 +
NOTE : If you don’t know or remember the formula for the volume of a triangular pyramid, you can derive it using calculus as follows :
 +
 
 +
Take a small triangular element in the pyramid. We know that it’s area is proportional to the height from the vertex to the base. Hence, we know that <math>\frac{A_{small element}}{A} = \frac{h^2}{H^2} \implies A_{small element} = \frac{Ah^2}{H^2}</math>. Now integrate it taking the limits <math>0</math> to <math>H</math>
 +
 
 +
===Shortcut===
 
Here is a shortcut for finding the radius <math>R</math> of the circumcenter of <math>\triangle ABC</math>.
 
Here is a shortcut for finding the radius <math>R</math> of the circumcenter of <math>\triangle ABC</math>.
  
Line 57: Line 62:
  
 
Then continue as before to use the Pythagorean Theorem on <math>\triangle AOP</math>, find <math>h</math>, and find the volume of the pyramid.
 
Then continue as before to use the Pythagorean Theorem on <math>\triangle AOP</math>, find <math>h</math>, and find the volume of the pyramid.
 +
 +
===Another Shortcut (Extended Law of Sines)===
 +
Take the base <math>\triangle ABC</math>, where <math>AB = BC = 20</math> and <math>AC = 24</math>. Draw an altitude from <math>B</math> to <math>AC</math> that bisects <math>AC</math> at point <math>D</math>. Then the altitude has length <math>\sqrt{20^2 - 12^2} = \sqrt{16^2} = 16</math>. Next, let <math>\angle BCA = \theta</math>. Then from the right triangle <math>\triangle BDC</math>, <math>\sin \theta = 4/5</math>. From the extended law of sines, the circumradius is <math>20 \cdot \dfrac{5}{4} \cdot \dfrac{1}{2} = \dfrac{25}{2}</math>.
  
 
==Solution 2 (Coordinates)==
 
==Solution 2 (Coordinates)==
Line 87: Line 95:
 
From this, we can determine the height of both <math>\triangle CPM</math> and tetrahedron <math>ABCP</math> to be <math>\frac{100\sqrt{3}}{8}</math>; therefore, the volume of the tetrahedron equals <math>\frac{100\sqrt{3}}{8} \cdot 192=800\sqrt{3}</math>; thus, <math>m+n=800+3=\boxed{803}.</math>
 
From this, we can determine the height of both <math>\triangle CPM</math> and tetrahedron <math>ABCP</math> to be <math>\frac{100\sqrt{3}}{8}</math>; therefore, the volume of the tetrahedron equals <math>\frac{100\sqrt{3}}{8} \cdot 192=800\sqrt{3}</math>; thus, <math>m+n=800+3=\boxed{803}.</math>
  
−
-dzhou100
+
'''-dzhou100'''
 +
 
 +
 
 +
==Solution 4 (Symmetry)==
 +
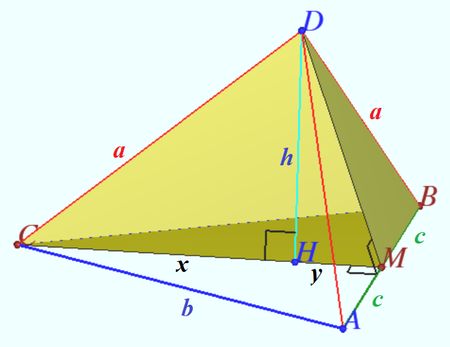
[[File:2017 AIME I 4.png|450px|right]]
 +
 
 +
Notation is shown on diagram.
 +
<cmath>AM = MB = c = 12, AC = BC = b = 20,</cmath>
 +
<cmath>DA = DB = DC = a = 25.</cmath>
 +
<cmath>CM = x + y = \sqrt{b^2-c^2} = 16,</cmath>
 +
<cmath>x^2 - y^2 = CD^2 – DM^2 = CD^2 – (BD^2 – BM^2) = c^2 = 144,</cmath>
 +
<cmath>x – y = \frac{x^2 – y^2}{x+y} = \frac {c^2} {16} = 9,</cmath>
 +
<cmath>x = \frac {16 + 9}{2} = \frac {a}{2},</cmath>
 +
<cmath>h = \sqrt{a^2 -\frac{ a^2}{4}} = a \frac {\sqrt{3}}{2},</cmath>
 +
<cmath>V = \frac{h\cdot CM \cdot c}{3}= \frac{16\cdot 25 \sqrt{3} \cdot 12}{3} = 800 \sqrt{3} \implies \boxed {803}.</cmath>
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
 
 +
==Video Solution==
 +
https://youtu.be/Mk-MCeVjSGc
 +
~Shreyas S
  
 
==See Also==
 
==See Also==
 
{{AIME box|year=2017|n=I|num-b=3|num-a=5}}
 
{{AIME box|year=2017|n=I|num-b=3|num-a=5}}
 
{{MAA Notice}}
 
{{MAA Notice}}

Latest revision as of 14:55, 5 January 2024

Problem

A pyramid has a triangular base with side lengths $20$, $20$, and $24$. The three edges of the pyramid from the three corners of the base to the fourth vertex of the pyramid all have length $25$. The volume of the pyramid is $m\sqrt{n}$, where $m$ and $n$ are positive integers, and $n$ is not divisible by the square of any prime. Find $m+n$.

Solution

Let the triangular base be $\triangle ABC$, with $\overline {AB} = 24$. We find that the altitude to side $\overline {AB}$ is $16$, so the area of $\triangle ABC$ is $(24*16)/2 = 192$.

Let the fourth vertex of the tetrahedron be $P$, and let the midpoint of $\overline {AB}$ be $M$. Since $P$ is equidistant from $A$, $B$, and $C$, the line through $P$ perpendicular to the plane of $\triangle ABC$ will pass through the circumcenter of $\triangle ABC$, which we will call $O$. Note that $O$ is equidistant from each of $A$, $B$, and $C$. Then,

\[\overline {OM} + \overline {OC} = \overline {CM} = 16\]

Let $\overline {OM} = d$. Then $OC=OA=\sqrt{d^2+12^2}.$ Equation $(1)$: \[d + \sqrt {d^2 + 144} = 16\]

Squaring both sides, we have

\[d^2 + 144 + 2d\sqrt {d^2+144} + d^2 = 256\]

\[2d^2 + 2d\sqrt {d^2+144} = 112\]

\[2d(d + \sqrt {d^2+144}) = 112\]

Substituting with equation $(1)$:

\[2d(16) = 112\]

\[d = 7/2\]

We now find that $\sqrt{d^2 + 144} = 25/2$.

Let the distance $\overline {OP} = h$. Using the Pythagorean Theorem on triangle $AOP$, $BOP$, or $COP$ (all three are congruent by SSS):

\[25^2 = h^2 + (25/2)^2\]

\[625 = h^2 + 625/4\]

\[1875/4 = h^2\]

\[25\sqrt {3} / 2 = h\]


Finally, by the formula for volume of a pyramid,

\[V = Bh/3\]

\[V = (192)(25\sqrt{3}/2)/3\] This simplifies to $V = 800\sqrt {3}$, so $m+n = \boxed {803}$.


NOTE : If you don’t know or remember the formula for the volume of a triangular pyramid, you can derive it using calculus as follows :

Take a small triangular element in the pyramid. We know that it’s area is proportional to the height from the vertex to the base. Hence, we know that $\frac{A_{small element}}{A} = \frac{h^2}{H^2} \implies A_{small element} = \frac{Ah^2}{H^2}$. Now integrate it taking the limits $0$ to $H$

Shortcut

Here is a shortcut for finding the radius $R$ of the circumcenter of $\triangle ABC$.

As before, we find that the foot of the altitude from $P$ lands on the circumcenter of $\triangle ABC$. Let $BC=a$, $AC=b$, and $AB=c$. Then we write the area of $\triangle ABC$ in two ways: \[[ABC]= \frac{1}{2} \cdot 24 \cdot 16 = \frac{abc}{4R}\]

Plugging in $20$, $20$, and $24$ for $a$, $b$, and $c$ respectively, and solving for $R$, we obtain $R= \frac{25}{2}=OA=OB=OC$.

Then continue as before to use the Pythagorean Theorem on $\triangle AOP$, find $h$, and find the volume of the pyramid.

Another Shortcut (Extended Law of Sines)

Take the base $\triangle ABC$, where $AB = BC = 20$ and $AC = 24$. Draw an altitude from $B$ to $AC$ that bisects $AC$ at point $D$. Then the altitude has length $\sqrt{20^2 - 12^2} = \sqrt{16^2} = 16$. Next, let $\angle BCA = \theta$. Then from the right triangle $\triangle BDC$, $\sin \theta = 4/5$. From the extended law of sines, the circumradius is $20 \cdot \dfrac{5}{4} \cdot \dfrac{1}{2} = \dfrac{25}{2}$.

Solution 2 (Coordinates)

We can place a three dimensional coordinate system on this pyramid. WLOG assume the vertex across from the line that has length $24$ is at the origin, or $(0, 0, 0)$. Then, the two other vertices can be $(-12, -16, 0)$ and $(12, -16, 0)$. Let the fourth vertex have coordinates of $(x, y, z)$. We have the following $3$ equations from the distance formula.

\[x^2+y^2+z^2=625\]

\[(x+12)^2+(y+16)^2+z^2=625\]

\[(x-12)^2+(y+16)^2+z^2=625\]

Adding the last two equations and substituting in the first equation, we get that $y=-\frac{25}{2}$. If you drew a good diagram, it should be obvious that $x=0$. Now, solving for $z$, we get that $z=\frac{25\sqrt{3}}{2}$. So, the height of the pyramid is $\frac{25\sqrt{3}}{2}$. The base is equal to the area of the triangle, which is $\frac{1}{2} \cdot 24 \cdot 16 = 192$. The volume is $\frac{1}{3} \cdot 192 \cdot \frac{25\sqrt{3}}{2} = 800\sqrt{3}$. Thus, the answer is $800+3 = \boxed{803}$.

-RootThreeOverTwo

Solution 3 (Heron's Formula)

Label the four vertices of the tetrahedron and the midpoint of $\overline {AB}$, and notice that the area of the base of the tetrahedron, $\triangle ABC$, equals $192$, according to Solution 1.

Notice that the altitude of $\triangle CPM$ from $\overline {CM}$ to point $P$ is the height of the tetrahedron. Side $\overline {PM}$ is can be found using the Pythagorean Theorem on $\triangle APM$, giving us $\overline {PM}=\sqrt{481}.$

Using Heron's Formula, the area of $\triangle CPM$ can be written as \[\sqrt{\frac{41+\sqrt{481}}{2}(\frac{41+\sqrt{481}}{2}-16)(\frac{41+\sqrt{481}}{2}-25)(\frac{41+\sqrt{481}}{2}-\sqrt{481})}\] \[=\frac{\sqrt{(41+\sqrt{481})(9+\sqrt{481})(-9+\sqrt{481})(41-\sqrt{481})}}{4}\]

Notice that both $(41+\sqrt{481})(41-\sqrt{481})$ and $(9+\sqrt{481})(-9+\sqrt{481})$ can be rewritten as differences of squares; thus, the expression can be written as \[\frac{\sqrt{(41^2-481)(481-9^2)}}{4}=\frac{\sqrt{480000}}{4}=100\sqrt{3}.\]

From this, we can determine the height of both $\triangle CPM$ and tetrahedron $ABCP$ to be $\frac{100\sqrt{3}}{8}$; therefore, the volume of the tetrahedron equals $\frac{100\sqrt{3}}{8} \cdot 192=800\sqrt{3}$; thus, $m+n=800+3=\boxed{803}.$

-dzhou100


Solution 4 (Symmetry)

2017 AIME I 4.png

Notation is shown on diagram. \[AM = MB = c = 12, AC = BC = b = 20,\] \[DA = DB = DC = a = 25.\] \[CM = x + y = \sqrt{b^2-c^2} = 16,\] \[x^2 - y^2 = CD^2 – DM^2 = CD^2 – (BD^2 – BM^2) = c^2 = 144,\] \[x – y = \frac{x^2 – y^2}{x+y} = \frac {c^2} {16} = 9,\] \[x = \frac {16 + 9}{2} = \frac {a}{2},\] \[h = \sqrt{a^2 -\frac{ a^2}{4}} = a \frac {\sqrt{3}}{2},\] \[V = \frac{h\cdot CM \cdot c}{3}= \frac{16\cdot 25 \sqrt{3} \cdot 12}{3} = 800 \sqrt{3} \implies \boxed {803}.\] vladimir.shelomovskii@gmail.com, vvsss

Video Solution

https://youtu.be/Mk-MCeVjSGc ~Shreyas S

See Also

2017 AIME I (Problems • Answer Key • Resources)
Preceded by
Problem 3 		Followed by
Problem 5
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2017_AIME_I_Problems/Problem_4&oldid=209965"