Difference between revisions of "1998 AIME Problems/Problem 3"
(→Solution) |
Made in 2016 (talk | contribs) m (→Solution) |
||
| Line 3: | Line 3: | ||
== Solution == | == Solution == | ||
| + | The equation given can be rewritten as: | ||
| + | |||
:<math>40|x| = - y^2 - 2xy + 400</math> | :<math>40|x| = - y^2 - 2xy + 400</math> | ||
Revision as of 14:07, 21 August 2017
Problem
The graph of ![]() partitions the plane into several regions. What is the area of the bounded region?
partitions the plane into several regions. What is the area of the bounded region?
Solution
The equation given can be rewritten as:
We can split the equation into a piecewise equation by breaking up the absolute value:
Factoring the first one: (alternatively, it is also possible to complete the square)
Hence, either ![]() , or
, or ![]() .
.
Similarily, for the second one, we get ![]() or
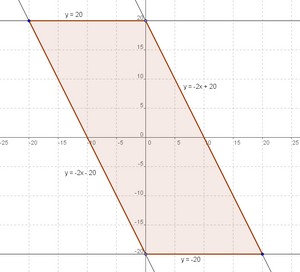
or ![]() . If we graph these four equations, we see that we get a parallelogram with base 20 and height 40. Hence the answer is
. If we graph these four equations, we see that we get a parallelogram with base 20 and height 40. Hence the answer is ![]() .
.
See also
| 1998 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 2 |
Followed by Problem 4 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.