1985 AIME Problems/Problem 4

Problem

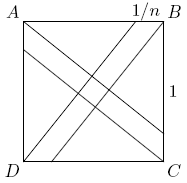
A small square is constructed inside a square of area 1 by dividing each side of the unit square into equal parts, and then connecting the vertices to the division points closest to the opposite vertices. Find the value of if the the area of the small square is exactly .

Solution 1

The lines passing through and divide the square into three parts, two right triangles and a parallelogram. Using the smaller side of the parallelogram, , as the base, where the height is 1, we find that the area of the parallelogram is . By the Pythagorean Theorem, the longer base of the parallelogram has length , so the parallelogram has height . But the height of the parallelogram is the side of the little square, so . Solving this quadratic equation gives .

Solution 2

Surrounding the square with area are right triangles with hypotenuse (sides of the large square). Thus, , where is the area of the of the 4 triangles. We can thus use proportions to solve this problem.

$\begin{eqnarray*} \frac{GF}{BE}=\frac{CG}{CB}\implies \frac{\frac{1}{\sqrt{1985}}}{BE}=\frac{\frac{1}{n}}{1}\implies BE=\frac{n\sqrt{1985}}{1985} \end{eqnarray*}$ (Error compiling LaTeX. Unknown error_msg)

Also,

$\begin{eqnarray*} \frac{BE}{1}=\frac{EC}{\frac{n-1}{n}}\implies EC=\frac{\sqrt{1985}}{1985}(n-1) \end{eqnarray*}$ (Error compiling LaTeX. Unknown error_msg)

Thus,

$\begin{eqnarray*} 2(BE)(EC)+\frac{1}{1985}=1\\ 2n^{2}-2n+1=1985\\ n(n-1)=992 \end{eqnarray*}$ (Error compiling LaTeX. Unknown error_msg)

Simple factorization and guess and check gives us .

See also

• AIME Problems and Solutions
• American Invitational Mathematics Examination
• Mathematics competition resources