Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2014 IMO Problems/Problem 4"

(→‎Solution 3)
m (→‎Solution 3)
Line 27: Line 27:
 
Let <math>L</math> be the midpoint of <math>BC</math>. By AA Similarity, triangles <math>BAP</math> and <math>BCA</math> are similar, so <math>\dfrac{BA}{AP} = \dfrac{BC}{CA}</math> and <math>\angle{BPA} = \angle{BAC}</math>. Similarly, <math>\angle{CQA} = \angle{BAC}</math>, and so triangle <math>AQP</math> is isosceles. Thus, <math>AQ = AP</math>, and so <math>\dfrac{BA}{AQ} = \dfrac{BC}{CA}</math>. Dividing both sides by 2, we have <math>\dfrac{BA}{AN} = \dfrac{BL}{AC}</math>, or
 
Let <math>L</math> be the midpoint of <math>BC</math>. By AA Similarity, triangles <math>BAP</math> and <math>BCA</math> are similar, so <math>\dfrac{BA}{AP} = \dfrac{BC}{CA}</math> and <math>\angle{BPA} = \angle{BAC}</math>. Similarly, <math>\angle{CQA} = \angle{BAC}</math>, and so triangle <math>AQP</math> is isosceles. Thus, <math>AQ = AP</math>, and so <math>\dfrac{BA}{AQ} = \dfrac{BC}{CA}</math>. Dividing both sides by 2, we have <math>\dfrac{BA}{AN} = \dfrac{BL}{AC}</math>, or
 
<cmath>\frac{BA}{BL} = \frac{AN}{AC}.</cmath>
 
<cmath>\frac{BA}{BL} = \frac{AN}{AC}.</cmath>
−
But we also have <math>\angle{ABL} = \angle{CAQ}</math>, so triangles <math>ABL</math> and <math>NAC</math> are similar by <math>SAS</math> similarity. In particular, <math>\angle{ANC} = \angle{BAL}</math>. Similarly, <math>\angle{BMA} = \angle{CAL}</math>, so <math>\angle{ANC} + \angle{BMA} = \angle{BAC}</math>. In addition, angle sum in triangle <math>AQP</math> gives <math>\angle{QAP} = 180^\circ - 2\angle{A}</math>. Therefore, if we let lines <math>BM</math> and <math>CN</math> intersect at <math>T</math>, by Angle Sum in quadrilateral concave <math>\angle{NTM} = 180^\circ + \angle{A}</math>, and so convex <math>\angle{BTC} = 180^\circ - \angle{A}</math>, which is enough to prove that <math>BACT</math> is cyclic. This completes the proof.
+
But we also have <math>\angle{ABL} = \angle{CAQ}</math>, so triangles <math>ABL</math> and <math>NAC</math> are similar by <math>SAS</math> similarity. In particular, <math>\angle{ANC} = \angle{BAL}</math>. Similarly, <math>\angle{BMA} = \angle{CAL}</math>, so <math>\angle{ANC} + \angle{BMA} = \angle{BAC}</math>. In addition, angle sum in triangle <math>AQP</math> gives <math>\angle{QAP} = 180^\circ - 2\angle{A}</math>. Therefore, if we let lines <math>BM</math> and <math>CN</math> intersect at <math>T</math>, by Angle Sum in quadrilateral <math>AMTN</math> concave <math>\angle{NTM} = 180^\circ + \angle{A}</math>, and so convex <math>\angle{BTC} = 180^\circ - \angle{A}</math>, which is enough to prove that <math>BACT</math> is cyclic. This completes the proof.
  
 
--[[User:Suli|Suli]] 10:38, 8 February 2015 (EST)
 
--[[User:Suli|Suli]] 10:38, 8 February 2015 (EST)

Revision as of 13:38, 16 February 2015

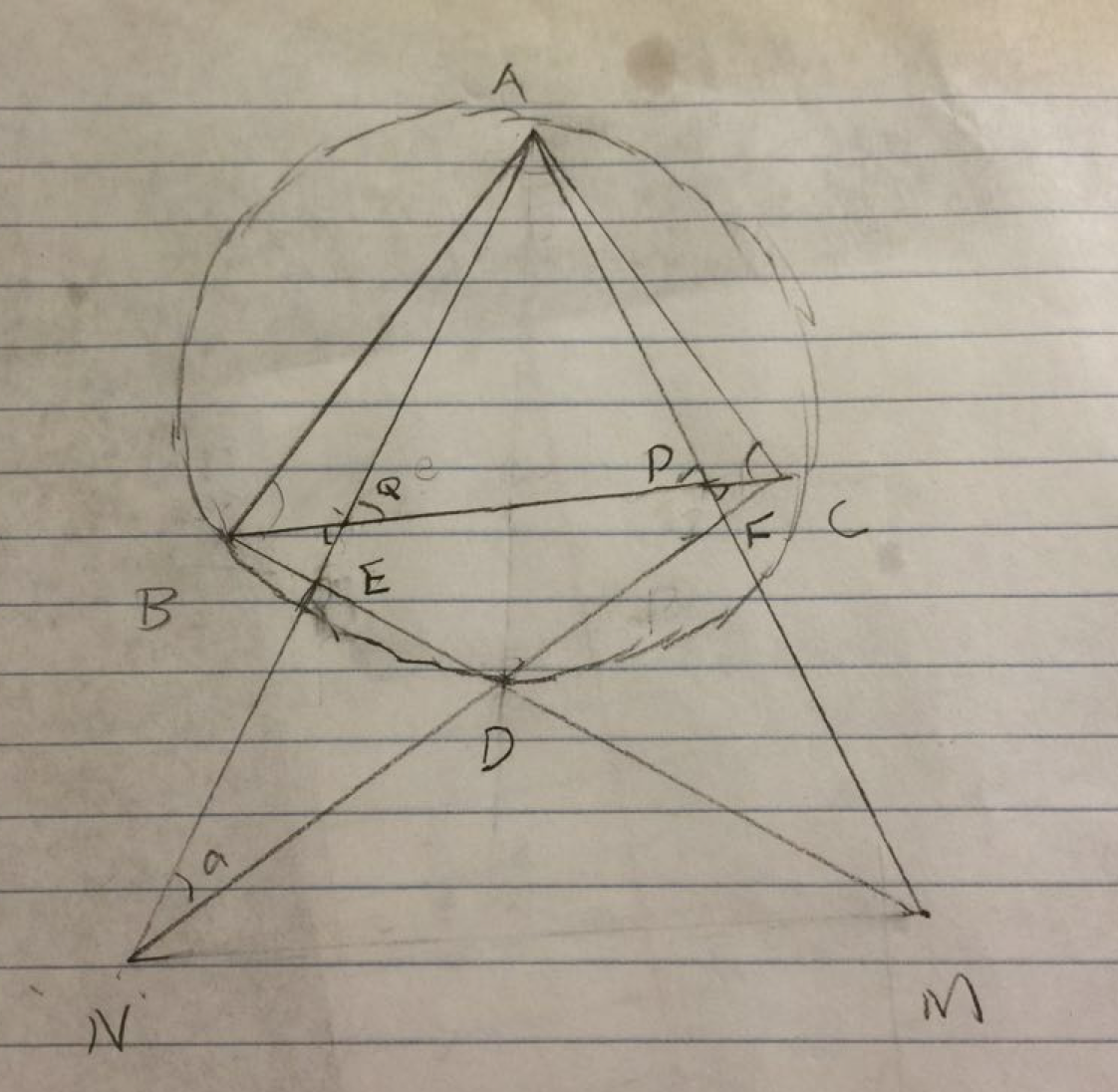
Problem

Points $P$ and $Q$ lie on side $BC$ of acute-angled $\triangle{ABC}$ so that $\angle{PAB}=\angle{BCA}$ and $\angle{CAQ}=\angle{ABC}$. Points $M$ and $N$ lie on lines $AP$ and $AQ$, respectively, such that $P$ is the midpoint of $AM$, and $Q$ is the midpoint of $AN$. Prove that lines $BM$ and $CN$ intersect on the circumcircle of $\triangle{ABC}$.

Solution

Screen Shot 2015-01-13 at 4.04.54 PM.png

Sorry guys I'm new to AOPS so I don't know how to insert equations and stuff. Please help if you can. Thanks.

We are trying to prove that the intersection of BM and CN, call it point D, is on the circumcircle of triangle ABC. In other words, we are trying to prove angle BAC plus angle BDC is 180 degrees. Let the intersection of BM and AN be point E, and the intersection of AM and CN be point F. Let us assume (angle BDC) + (angle BAC) = 180. Note: This is circular reasoning. If angle BDC plus angle BAC is 180, then angle BAC should be equal to angles BDN and CDM. We can quickly prove that the triangles ABC, APB, and AQC are similar, so angles BAC = AQC = APB. We also see that angles AQC = BQN = APB = CPF. Also because angles BEQ and NED, MFD and CFP are equal, the triangles BEQ and NED, MDF and FCP must be two pairs of similar triangles. Therefore we must prove angles CBM and ANC, AMB and BCN are equal. We have angles BQA = APC = NQC = BPM. We also have AQ = QN, AP = PM. Because the triangles ABP and ACQ are similar, we have EC/EN = BF/FM, so triangles BFM and NEC are similar. So the angles CBM and ANC, BCN and AMB are equal and we are done.

Solution 2

Let $L$ be the midpoint of $BC$. Easy angle chasing gives $\angle{AQP} = \angle{APQ} = \angle{BAC}$. Because $P$ is the midpoint of $AM$, the cotangent rule applied on triangle $MBA$ gives us \[\cot \angle{MBC} - \cot \angle{ABC} = 2\cot \angle{BAC}.\] Hence, by the cotangent rule on $ABC$, we have \[\cot \angle{BAL} = 2\cot \angle{BAC} + \cot \angle{ABC} = \cot \angle{MBC}.\] Because the period of cotangent is $180^\circ$, but angles are less than $180^\circ$, we have $\angle{BAL} = \angle{MBC}.$

Similarly, we have $\angle{LAC} = \angle{NCB}.$ Hence, if $BM$ and $CN$ intersect at $Z$, then $\angle{BZC} = 180^\circ - \angle{BAC}$ by the Angle Sum in a Triangle Theorem. Hence, $BACZ$ is cyclic, which is equivalent to the desired result.

--Suli 23:27, 7 February 2015 (EST)

Solution 3

Let $L$ be the midpoint of $BC$. By AA Similarity, triangles $BAP$ and $BCA$ are similar, so $\dfrac{BA}{AP} = \dfrac{BC}{CA}$ and $\angle{BPA} = \angle{BAC}$. Similarly, $\angle{CQA} = \angle{BAC}$, and so triangle $AQP$ is isosceles. Thus, $AQ = AP$, and so $\dfrac{BA}{AQ} = \dfrac{BC}{CA}$. Dividing both sides by 2, we have $\dfrac{BA}{AN} = \dfrac{BL}{AC}$, or \[\frac{BA}{BL} = \frac{AN}{AC}.\] But we also have $\angle{ABL} = \angle{CAQ}$, so triangles $ABL$ and $NAC$ are similar by $SAS$ similarity. In particular, $\angle{ANC} = \angle{BAL}$. Similarly, $\angle{BMA} = \angle{CAL}$, so $\angle{ANC} + \angle{BMA} = \angle{BAC}$. In addition, angle sum in triangle $AQP$ gives $\angle{QAP} = 180^\circ - 2\angle{A}$. Therefore, if we let lines $BM$ and $CN$ intersect at $T$, by Angle Sum in quadrilateral $AMTN$ concave $\angle{NTM} = 180^\circ + \angle{A}$, and so convex $\angle{BTC} = 180^\circ - \angle{A}$, which is enough to prove that $BACT$ is cyclic. This completes the proof.

--Suli 10:38, 8 February 2015 (EST)

Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.

See Also

2014 IMO (Problems) • Resources
Preceded by
Problem 3 		1 • 2 • 3 • 4 • 5 • 6 Followed by
Problem 5
All IMO Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2014_IMO_Problems/Problem_4&oldid=67860"